电力电缆运行故障仿真分析研究

2020-06-06翟荣刚

合肥学院学报(综合版) 2020年2期

翟荣刚，杨威，高原，沙静

(1.安徽邮电职业技术学院通信工程系，合肥 230031;2.安徽医学高等专科学校基础部，合肥 230601)

0 引言

在社会发展中，电力作为最重要的能源，扮演着重要角色。而电力传输系统作为电力传输的基本保证和唯一途径，不断发展和更新。目前，在城市内部，架空传输线路逐渐被各种安装形式的电力电缆所替代。城市中敷设电缆方式基本包括直埋敷设、浅槽敷设、隧道敷设。[1]然而，为了方便维护，城市内部常采用电缆沟敷设和电缆隧道敷设。它们作为最有效的和最简便的敷设城内电缆敷设方式。但是，随着城市扩大带来用电量的增加，电力企业不得不扩大电网供电范围以应对市场变化。[2]通过调查研究发现，负荷电缆长时间运行会增加供配电系统的故障率，同时还会加速电缆的老化。[3]

目前，城市内常采用地下敷设电缆。尽管这种方式有诸多优点，但是，一旦出现故障，就很难准确确定故障类型和对故障点定位。为了快速精确查找故障类型和故障点，不仅会浪费掉大量人力、物力，同时还会给社会带来极大的停电损失以及经济损失。由于我国电缆安装和维护得不到重视，尽管城市输配电网大量采用地下敷设，但线路安装质量以及维护技术水平相比西方发达国家较落后。通过调查分析，现在研究电力电缆主要集中在机械损伤、绝缘受潮、电缆接头故障和绝缘老化变质等几个方面。[4]这些基本都是外在环境因素或施工不当而引起的电力电缆故障。当供配电系统建设完成之后，研究电力系统运行中由于绝缘受潮或绝缘老化引起的电力系统电力电缆短路故障分析的较少。[5]本文研究因受潮、绝缘老化、过电压、机械损伤等因素引起的电力电缆运行的各种短路故障。分析供配电系统中电力电缆短路故障引起的电压或电流变化，并使用MATLAB/Simulink仿真各种短路故障类型，分析电压和电流的变化形式，判断故障模式，为下一步查找故障点和电力故障维修提供有力的证据。

1 电力系统短路故障分析

供配电系统运转过程中不可避免地出现不正常状况和各种故障。而最严重故障就属于短路故障。短路故障就是相与相或相与地之前的直接相连或通过一小阻抗相连。[6]通过调查分析发现，在中性点直接接地供配电系统中，以单相短路故障最多，而三相短路故障出现的概率最小。然而，三相短路故障在各类故障中对供配电系统造成的危害却最严重。[7]因此本文以三相短路故障和单相短路故障为例分析。在故障计算之前，做如下假设[8]：(1)不考虑发电机间的摇摆现象和磁路饱和。(2)假设发电机是对称的，不对其做过细的讨论。(3)因为短路电流远大于正常电流，相比之下，可以不计变压器对地导纳。(4)忽略电力线路的对地电容。(5)忽略电力电缆线路的电阻。(6)研究的供配电系统为无限大容量电源系统。

1.1 三相短路故障分析

供配电系统出现三相短路故障的电路模型[9]，如图1所示。供配电系统短路前，系统一直保持在某一稳定状态。由于供配电系统是对称的，可只写其中任意一相(a相)的电压和电流的表达式，即

(1)

(2)

(3)

(4)

式(3)、(4)中，R1+R2和L1+L2分别为短路前a相的电阻和电感，Um为短路前系统电压幅值，Im为短路前系统电流幅值。

图1 电力系统三相短路故障

当电力系统出现三相短路故障时，系统被分为两部分，即2个独立回路。左边部分保持与电源连接，而右侧则成为无源的短路回路。在右侧短路系统中，电流将从短路发生瞬间的初始值按指数规律衰减到0。在衰减过程中，该电路系统的磁场中存储的所有能量将全部被电阻消耗，转化为热能。在左侧回路中，每相阻抗由 (R1+R2)+jw(L1+L2)。电流由正常工作值逐渐转化成由所决定的短路稳态电流值。

假设三相短路故障在t=0时出现，左侧系统回路仍对称，则只需研究其中一相，即a相的微分方程。根据式(1)和式(2)，结合基尔霍夫定律，可列出a相的微分方程为

(5)

其解为

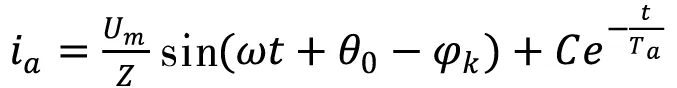
(6)

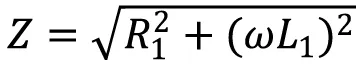
将t=0代入式(6)中，可得瞬时短路的电流为

(7)

根据电力系统特性，短路瞬间电流回路的电流不会突变，仍等于故障前的瞬时值。根据电路的暂态分析，采用环路定律，由式(2)可得

(8)

由式(7)和式(8)，利用电路暂态分析中的三要素法，可得

(9)

由式(8)、式(9)和式(6)，可得a相电流表达式

(10)

1.2 单相短路故障分析

单相短路故障又称不对称短路故障。该故障只是在故障点出现系统结构的不对称，而其它部分仍对称。根据对称分量理论，可将单相短路故障分解为正、负、零序三个独立系统。将故障点的不对称电压和电流分别用它们的三序分量替代，从而形成正、负、零序三个等值网络。[10]

根据分析可得单相接地短路故障的边界条件：

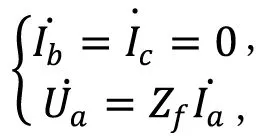
(11)

用对称分量表示边界条件，可将短路点三相电流转换为三序电流，即

(12)

由式(12)可得，故障点各序电流相等，均为故障相电流的1/3，即

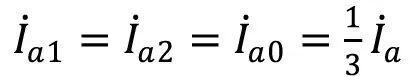
(13)

2 仿真结果与分析

对无限大功率电源供电系统模型通过MATLAB/Simulink对电力电缆供电系统进行故障仿真分析。观察电压、电流在故障前后的变化，与实际结果相比较，从而得出相应结论。在系统中各个参数设置为：线路长度L=100kM，线路电抗X=0.4Ω/kM，线路电阻r=0.17Ω/kM；变压器的额定容量Sn=200MV·A，高低压绕组均为Y形联结，空载电流I0=0.8A，空载损耗P1=0.8kW，短路损耗P=135W，变比K=110/11。供电电压为UL=110kV。在电力系统短路分析时，主要观察三相短路、两相短路、两相接地短路及单相接地短路故障时的电压和电流变化情况，便可得出系统故障类型。因在中性点直接接地供配电系统中，以单相短路故障最多，而三相短路故障出现的概率最小。然而，三相短路故障在各类故障中对供配电系统造成的危害却最严重。因此，本文以正常运行、三相短路故障和单相短路故障为例分析。

(1)正常运行时，供电系统电压、电流波形都呈现正弦波，如图2所示和图3所示。

图2 供用电系统正常运行电压波形

图3 供电系统正常运行电流波形

(2)假设0.1s～0.15s三相短路故障。通过与图2和图3相比，三相短路接地故障时，三相电压在0.1s突然变为零，经过0.15s后故障消除，电压回复如图4所示。因正常运行时电流比三相故障电流小得多。因此，在故障时的电流很大，正常电流几乎为0。故障消除后，电压电流都恢复正常，如图5所示。

图4 三相短路故障电压波形

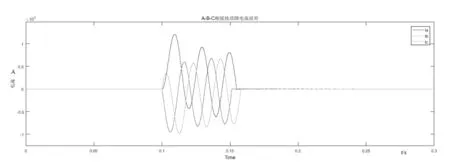
图5 三相短路故障电流波形

(3)假设0.1s～0.15s发生a相短路故障。通过与图2和图3相比，a相短路接地故障时，a相电压在0.1s突然变为零，经过0.15s后故障消除，电压回复。然而，b相和c不受影响而相正常运行，如图6所示。a相电流在0.1s发生突变，相比其他两相短路电流值很大。故障切除后，电流电压都恢复正常，如图7所示。

图6 a相接地故障电压波形

图7 a相接地故障电流波形

(4)假设0.1s～0.15s发生ab相短路故障(由于ac故障或bc故障波形与ab故障波形类似，只是发生突变相序不同，不作过多描述)。ab相发生短路接地故障时，ab两相相电压在0.15s突然变为零，经过一段时间变化后故障消除，电压回复如图8所示。然而，c不受影响而相正常运行。ab相在发生故障时产生了一个瞬时的尖峰故障电流，如图9所示。

图8 ab两相电压故障波形

图9 ab两相电流故障波形

通过分析图2至图9波形对比可以得出，电力电缆在正常运行中电压和电流不会发生突变，只有发生故障时，电压与电流波形才能发生突变。电压波形突变随着故障的存在一直会持续，而电流波形出现在故障发生的瞬间，随后消失。通过对比发现，与正常运行相比，电流瞬间突变往往比正常值大得多，对系统造成的影响更大，损害更加严重。