基于主成分分析和区域增长的结构光中心线提取

2020-06-06何坚强侯建成汪志成

科学技术与工程 2020年12期

何坚强,侯建成,汪志成

(1.盐城工学院电气工程学院，盐城 224000；2.江苏大学电气信息工程学院，镇江 212000)

结构光的图像位置是三维测量中的信息来源，因此，结构光中心提取是线结构光三维测量中至关重要的一步。中外学者做了大量的研究，针对不同的应用领域提出众多结构光中心提取方法。

目前结构光中心提取可以分为两类[1-2]，第一类是对结构光几何中心的提取，主要有细化法、边缘法和阈值法等[3-5]，这类方法容易受到噪声的影响，鲁棒性差，不适用于对提取精度要求较高的测量领域。第二类方法是根据结构光横截面的灰度值呈高斯分布的特点提取结构光中心，主要有灰度重心法、方向模板法和Steger法等[6-8]，这类方法中心提取精度较高，具有一定的抗干扰能力。特别是Steger法[9]稳定性好、提取精度高，得到广泛应用，但是运算量大。因此中国学者提出了众多改进算法。蔡怀宇等[10]引入主成分分析算法确定图像的法线方向，只用2次高斯卷积就可完成，降低了计算的复杂度，提高了计算速度，但是在复杂背景下很难实现结构光的精准提取；岳龙等[11]针对宽度变化复杂的激光条纹采用一种自适应条纹中心提取算法，根据条纹不同宽度选择对应的尺度因子，在一定程度上减少了计算量，实现了对于宽度变化复杂光条纹的中心线提取；杨镇豪等[12]将极值法和Steger方法相结合，通过线宽分段的方式实现在高反情况下结构光中心线的高精度提取，但是计算量较大；刘剑等[13]提出一种基于Hessian矩阵与区域增长相结合的激光条纹中心提取方法，该算法提取的条纹中心准确高，提取速度快。但是依赖Hessian矩阵求取法线方向，需要大规模的高斯卷积。

针对实际工程中结构光环境复杂，被测物体表面反光的情况，提出一种基于主成分分析与区域增长的结构光中心提取方法。首先通过图像掩模原理获得结构光的感兴趣区域(region of interest,ROI)；然后对ROI进行二维高斯卷积计算该区域的灰度梯度分布；根据梯度分布情况确定结构光中心的初始点；利用主成分分析算法求取初始点的法线方向，通过二阶泰勒展开求得该点的精确位置；最后以初始点为种子点通过区域增长迭代运算，精确提取结构光中心线。

1 结构光区域的提取

采集到的彩色图像中，结构光颜色与被测物体颜色存在很大的差异，结构光为红色条纹，被测物体为银灰色背景，因此可以利用RGB颜色空间模型[14]将彩色图像分成目标区和背景区。利用这一特性，对图像上的每个像素点的RGB进行判断，结构光区域置1，背景区置0。但是由于表面反光和漫反射的影响会带来大量的噪声信息，利用形态学运算去除噪声得到掩模图像，然后掩模图像与灰度化后的图像相乘，得到结构光的ROI。掩模原理[15]可以表述为

F(X,Y)=H(x1,y1)M(x2,y2)

(1)

式(1)中：H(x1,y1)为掩模图像；M(x2,y2)表示待处理图像；F(X,Y)为输出图像。掩模法提取出的ROI更好地保留了结构光条纹的灰度，消除了金属面反光和结构光漫反射带来的影响，实现结构光区域的精确定位。

2 方向的计算

Hessian矩阵求取结构光法线方向时需要进行大规模的高斯卷积，计算量很大。通过二维高斯卷积和主成分分析(principal component analysis,PCA)实现对ROI法线和切线方向的求解[16]。

2.1 梯度分布

首先对结构光的ROI进行二维高斯卷积计算，ROI区域的灰度梯度如式(2)所示:

G=f(x,y)⊗g(x,y)

(2)

(3)

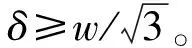
2.2 切向和法线

二维高斯卷积之后，得到ROI的梯度分布图，如果用(Gx,Gy)T表示梯度向量，则梯度向量的协方差矩阵为

(4)

其中：

(5)

利用PCA对梯度向量的协方差矩阵进行特征分解，最大特征值对应的特征向量就是法线方向。

经过计算得到特征值和相应的特征向量如下：

(6)

(7)

(8)

(9)

式中：特征值λ1、λ2对应的特征向量为v1，v2。由于|λ1|>|λ2|，所以特征向量v1为条纹的法线方向，归一化处理之后根据法线方向得到法线方向的单位向量n=(nx,ny)T。

3 结构光中心线

3.1 初始点的计算

得到目标区域的梯度分布后，选取梯度绝对值最小的点作为提取条纹中心的初始位置记为(x0,y0)。对初始点(x0,y0)的灰度分布函数沿法线方向进行二阶Taylor展开，则结构光横截面上的坐标点(x0+tnx,y0+tny)的灰度为

Z(x0+tnx,y0+tny)=Z(x0,y0)+N(Gx,Gy)T+

(10)

式(10)中：N=(tnx,tny)。因为极值所在点的一阶导数过零点，即：

(11)

综上可得：

(12)

则点(x0+tnx,y0+tny)为结构光中心点的精确位置。

3.2 区域增长提取结构光中心线

以初始点为种子，设置角度阈值和灰度阈值作为生长准则，种子点周围的8邻域作为生长区域，如果8邻域中存在一点，其角度差和灰度差满足设定的阈值条件，则认为该点为结构光的中心点，并将其作为新的生长点。具体的实现步骤如下。

(1)通过图像掩模法获得结构光的ROI，消除结构光的漫反射和金属表面反光的影响。

(2)计算ROI中的梯度，建立梯度向量的协方差矩阵，运用PCA分析得到种子点的法线和切线方向。

(3)将梯度最小的点作为初始点，并对其灰度分布函数沿法线方向进行二阶泰勒展开，获得初始点的精确位置。

(4)将初始点作为种子点，计算与周围的8邻域像素点之间法线的角度差和灰度差。如果存在一点满足角度差与灰度差的阈值条件，将此点与种子点合并为同一区域，作为新的生长点。

(5)把新的生长点作为种子，重复步骤(3)～步骤(4)，直到历遍ROI中的每个像素点，最终得到结构光条纹的中心线。

4 实验与分析

实验对象是温控器，温控器是一种金属材质的电路保护装置，表面反光。并且被测面并非平面，而是呈现出凹凸不平，因此，结构光漫反射情况严重。实物图和反光标记图如图1所示。为了验证方法的有效性和准确性，在MATLAB R2015b开发环境下对800×1 200像素的图像进行处理。

首先对结构光图像进行掩模处理，得到掩模图像和处理后的效果(图2)。通过图像掩模法可以实现结构光ROI的精确提取，并且保证了结构光的原始灰度。

图1 温控器图像Fig.1 Temperature controller image

图2 掩模处理结果Fig.2 Mask processing results

图3 三种方法提取结果Fig.3 The results of three mothods

为了进一步证明算法的优越性，分别与传统的灰度重心法，Steger法在中心线提取效果和运行时间两方面进行了比较。首先是提取效果的对比，图3(a)是灰度重心法提取的结构光中心线，由于受到结构光漫反射的影响，提取出结构光中心线出现了离散点，并且由于噪声的干扰提取的中心线位置并不精确。图3(b)为自适应Steger法提取的中心线，自适应分割算法不能消除结构光漫反射和金属表面反光的影响，因此引入了大量的干扰区域，提取效果较差。图3(c)为本文算法提取出的中心线，不仅从根本上解决了干扰区域的问题，而且提取的中心线连续没有断点，实现了结构光中心线的精确提取。本文方法的处理结果与光条的变化方向吻合，处理精度高，克服了光学条件的影响，具有很好的鲁棒性。

为了更加直观地展示三种方法提取的精度，通过最小二乘法对三种实验结果进行曲线线拟合，计算所有结构光中心到拟合曲线的均方差，如表1所示。

三种算法在提取8幅图片结构光中心线时所用的平均处理时间如表2所示。