定常不可压Navier-Stokes方程的并行有限元算法

尚月强，郑 波，周康瑞，丁 琪

(西南大学 数学与统计学院，重庆 北碚 400715)

0 引言

Navier-Stokes(N-S)方程组是流体力学的基本方程组，出现于许多理论与应用研究领域，如地球物理科学、水动力学、航天航空学、石油工业等，其研究对我国的经济与国防建设、工业设计具有非常重要的现实意义。然而，尽管对N-S方程的理论研究由来已久，数学上，三维N-S方程解的存在性与光滑性还没解决，是千禧年七大数学难题之一[1]；物理上，许多基本问题也还未弄清楚(如：湍流的惯性区统计的间歇性修正问题，粘性与大尺度效应等)[2]。这使得数值模拟成为一种十分重要的研究手段，N-S方程的数值模拟方法更是当前科学与工程计算研究中的前沿热门课题之一。

不可压N-S方程的有限元数值模拟存在诸多困难：1)非线性，N-S方程是一种典型的非线性方程，数值求解中需采用合适的迭代格式进行线性化处理；2)不可压缩性，N-S方程中的不可压缩条件(连续方程)将速度变量与压力变量耦合在一起，使得速度和压力的有限元空间需满足离散的inf-sup条件；3)大雷诺数问题，当雷诺数较大时，N-S方程对流占优，数值逼近中会出现伪震荡；4)大规模计算问题，存在巨大的求解规模和有限的计算资源之间的矛盾。特别是高维复杂区域上N-S方程的数值模拟，不论是计算规模还是存储需求，单机难以满足其需求，因此，需借助并行计算技术，实现N-S方程的快速大规模并行数值模拟。然而，要实现并行计算，除了高性能并行机、一套完善的并行编程系统软件外，高效的并行算法更是不可缺少的重要组成部分，它无论是对N-S方程的高效数值模拟，还是对提高并行机的运行效率，都起着至关重要的作用。

近年来，尽管并行计算技术取得了长足进步，但并行编程软件远远落后于并行计算机硬件的发展，使得并行编程的难度远远大于串行编程，制约了并行计算的发展。因此，一个并行算法除了应具有一个数值方法所应具有的数学特征(如稳定性、收敛性、有效性)外，还需实现简单、通信需求少、具有良好的可扩展性，才具有广阔的应用前景，这在多核处理器普及的今天，显得尤为重要。正是基于此认识，一类简单而高效的局部与并行有限元离散方法受到业界的普遍关注。该类方法最先由许进超教授和周爱辉教授针对非线性椭圆边值问题提出[3]，其基本思想是基于对有限元解的局部与整体性质的认识(即解的整体性质主要由低频分量控制，可用粗网格较好地逼近, 其局部性质则由高频分量控制，可在细网格上局部和并行计算)，首先在一粗网格上求解一个非线性问题，得粗网格的有限元解，然后在相互重叠的细网格子区域上局部与并行求解一个线性化的残差问题，以校正粗网格的有限元解。由于该类方法实现简单、通信需求少、具有良好的并行性能，被广泛应用于求解各种问题，如特征值问题[4-6]、Stokes问题[7-11]、N-S问题[12-17]、磁动流体力学问题[18-20]、Stokes/Darcy流问题[21]，N-S/Darcy流问题[22]、四阶微分方程[23]等；特别地，将该局部与并行有限元离散方法与区域分解算法和使用同阶元的压力稳定化方法相结合，我们分别研究了Stokes方程的Schwarz区域分解方法[24]和并行稳定化方法[25]，同时与完全重叠型区域分解技巧和求解大雷诺数问题的稳定化方法相结合，研究了从小雷诺数到大雷诺数N-S方程的系列并行算法[26-36]。理论分析与数值试验验证了这类算法的高效性。

基于局部与并行有限元离散技巧，结合区域分解方法，本文主要讨论N-S方程的简单而高效的并行有限元算法。这些算法实现简单，稍加修改现有的串行程序即可实现并行计算,可充分利用现有的串行软件进行并行编程，通信需求少，能快速有效地模拟复杂的流体流动行为。我们将给出这些算法的描述、相关理论结果和数值算例，验证算法的有效性。

本文内容安排如下：第1节，给出N-S方程及其混合有限元数值逼近的相关知识；第2节，给出两种并行策略；第3节，给出Dirichlet边界条件N-S方程的完全重叠型区域分解并行算法；第4节，给出Dirichlet边界条件N-S方程的并行两水平有限元算法；第5节，讨论非线性滑移边界条件N-S方程并行有限元算法；第6节，结束语。

1 N-S方程及其有限元逼近

1.1 不可压N-S方程

设Ω是Rn(n=2,3)中具有Lipschitz连续边界的有界开集，我们考虑下列定常不可压N-S方程:

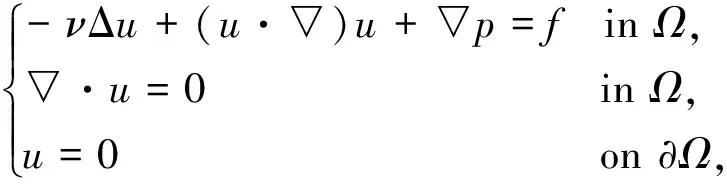
(1)

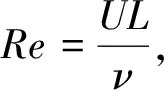
我们引入Hilbert空间：

并定义a(u,v),b(u,v,w),d(v,q)如下：

a(u,v)=ν(▽u,▽v),d(v,q)=(▽·v,q),

本文用(·,·)表示L2(Ω)n(n=1,2,3)上的标准内积,用‖·‖m表示Hm(Ω)n(m≥0)的范数。方程(1)的变分形式为:求(u,p)∈X×M, 满足

a(u,v)+b(u,u,v)-d(v,p)+d(u,q)=(f,v), ∀(v,q)∈X×M。

(2)

1.2 混合有限元逼近

设Tμ(Ω)={K}是Ω的一个尺寸为μ(0<μ<1,μ=H,h,H>h)的正则网格剖分，Xμ(Ω)⊂X,Mμ(Ω)⊂M是相应于网格Tμ(Ω)的两个有限元空间，

Xμ0(Ω) =Xμ(Ω)∩X,Mμ0(Ω) =Mμ(Ω)∩M。

给定G⊂⊂Ω0⊂Ω(这里G⊂⊂Ω0⊂Ω表示dist(∂G∂Ω0, ∂Ω0∂Ω)>0)，我们定义Xμ(G),Mμ(G)和Tμ(G)分别是Xμ(Ω),Mμ(Ω)和Tμ(Ω)在G上的限制，

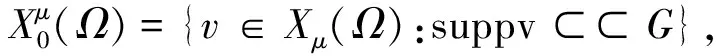
关于混合有限元空间的假设如下：对任何(u,p)∈Hk+1(G)×Hk(G)(k≥1),存在(πμu,ρμp)∈Xμ(G)×Mμ(G),使得

‖μ-1(u-πμu)‖0,G+‖u-πμu‖1,G≤

cμs‖u‖s+1,G0≤s≤k,

‖μ-1(p-ρμp)‖-1,G+‖p-ρμp‖0,G≤

cμs‖p‖s,G0≤s≤k。

(3)

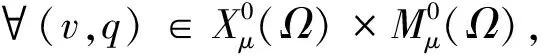
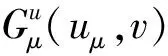
是标准的L2-投影：

1) 亚格子模型方法：

2) 基于两个Gauss积分的变分多尺度方法：

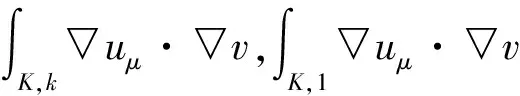
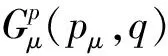
2 并行策略

我们首先对求解区域Ω进行区域分解，得到互不重叠的子区域D1,D2,…,Dm，然后将Dj向外扩展一定尺寸得到相互重叠的子区域Ωj，满足Dj⊂⊂Ωj⊂Ω(j=1,2,…,m)。

2.1 完全重叠型区域分解的并行策略

在该并行策略中，每台处理器根据流体在其所负责子区域上的物理特征，相互独立地生成一个局部加密的全局多尺度网格(该网格绝大部分自由度来自其所负责的子区域)，然后在该全局多尺度网格上使用有限元方法计算其所负责子区域上的局部有限元解。具体说来，处理器j与其他处理器相互独立地对其所负责的子区域Ωj生成尺度为h的细网格，对其余区域生成尺度为H>>h的粗网格，记所得的全局多尺度网格为Th,H(Ωj), 在这样的全局多尺度网格Th,H(Ωj)上使用有限元方法求解N-S方程，计算结束时取子区域Dj上的计算结果，得到子区域Dj上的局部有限元解。由于每个子问题的网格都覆盖整个区域，我们称这种并行策略为完全重叠型区域分解。图 1展示了两个子区域情形的完全重叠型区域分解。

2.2 基于两重网格离散的并行策略

在该并行策略中，我们分三步进行计算：1)在尺度为H的粗网格TH(Ω)上使用有限元方法求解非线性的N-S方程；2)使用区域分解技巧，在尺度为h的细网格Th(Ωj)上使用有限元方法并行求解线性化的局部残差方程；3)在细网格互不重叠的子区域Dj上并行校正有限元解。如图2所示：

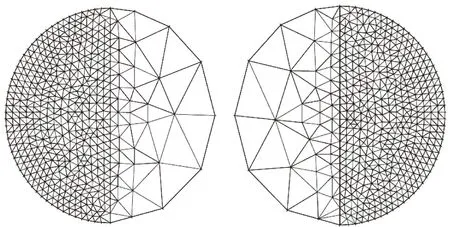
图1 完全重叠型区域分解Fig.1 A fully overlapping domain decomposition

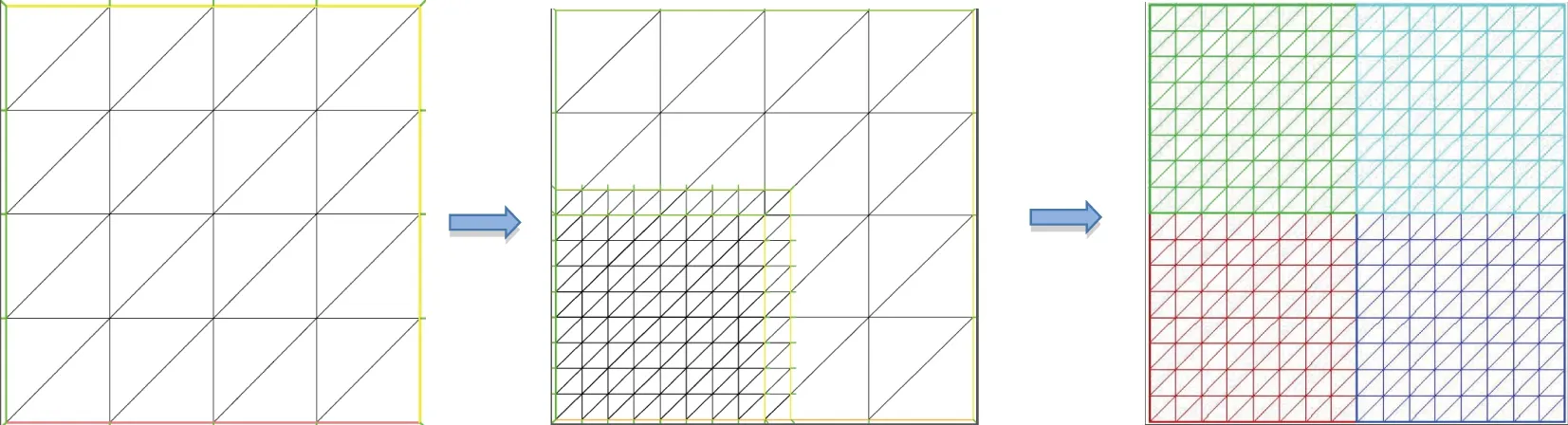
图2 基于两重网格离散的并行策略Fig.2 A parallel strategy based on two-grid discretizations

3 完全重叠型区域分解并行算法

本节考虑Dirichlet边界条件的N-S方程基于完全重叠型区域分解的并行算法，并分别考虑大雷诺数问题和使用同阶元的并行稳定化方法。

3.1 算法描述及理论结果

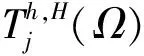
算法A 完全重叠型区域分解并行算法

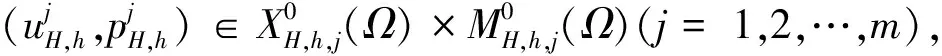
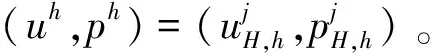
备注3.1：

1)算法A的每一个子问题事实上是一个全局问题，但它用来求解在特定子区域的局部有限元解；

2)上述算法中，各处理器可自适应地根据所模拟的流体在各自所负责子区域上的物理特征，相互独立地生成恰当的网格，选取恰当的有限元函数空间、稳定化方法及代数方程组的求解器进行计算，具有很大的灵活性；

3)上述算法中，各处理器相互独立地完成所有计算，无需交换数据，使得算法实现简单，稍加修改现有的串行程序即可实现并行计算，具有良好的并行性能；

4)上述算法得到的有限元解时分片连续的，在整个区域上是间断的。为了得到整体连续的有限元解，可在原算法的基础上增加一后处理步，如文[3]及[37-38]的方法。

对于上述算法，使用inf-sup稳定的混合有限元(即速度和压力的有限元空间满足离散的inf-sup条件，此时压力稳定项=0)，在一定的准确解的正则条件下，我们有下列收敛性结果[34]：

|||▽(u-uh)|||0,Ω+|||p-ph|||0,Ω≤c(hs+Hs+1+α),1≤s≤t。

其中，α是速度稳定项的系数，|||·|||0,Ω=

3.2 数值算例

算例1 已知准确解[34]

针对已知准确解的数值算例：

u1=10x2(x-1)2y(y-1)(2y-1),

u2=-10y2(y-1)2x(x-1)(2x-1),

p=x2-y2。

我们将求解区域Ω=[0,1]×[0,1]分解成4个子区域

D1=(0,1/2)×(0,1/2),

D2=(1/2,1)×(0,1/2),

D3=(1/2,1)×(1/2,1),

D4=(0,1/2)×(1/2,1),

并使用二阶Taylor-Hood元进行了数值试验，验证了理论分析的正确性，数值结果如表 1所示。

表1 算法A所得近似解的误差Tab.1 Errors of approximate solutions by Algorithm A

同时，针对不同的粘性系数，我们比较了使用不同的稳定化方法的计算结果，即变分多尺度方法(Variational multiscale method), 亚格子稳定化方法(Subgrid stabilized method)和不使用稳定化方法(Method without stabilization)。表2表明，对于大粘性系数(即小雷诺数)问题，相对于不使用稳定化方法，算法中所使用的稳定项没有影响近似解的精度；而对于小粘性系数(即大雷诺数)问题，稳定化方法的使用非常必要(如表2中，当ν=0.000 1时，不使用稳定化方法根本得不到有限元解)。

表2 基于不同稳定化方法的并行算法比较Tab.2 Comparison of numerical results by different parallel algorithms based on different stabilization methods

算例2后台阶流[34]

我们还将算法应用于后台阶流的数值模拟，图 3比较了雷诺数Re=800时我们的计算结果与文献中的数据比较，图4和图5分别描绘了Re=800、1 000时计算所得的流线和压力等值线。

算例3 方腔驱动流[36]

算法A中的问题是非线性问题，实际计算中需要采用迭代方法进行线性化处理。使用同阶的P1-P1元和基于两个Gauss积分的压力稳定化方法，我们考查了3种不同的迭代方法，即Newton迭代法、Oseen迭代法和Stokes迭代法, 得到了不同的稳定性条件和相应的收敛性结果，同时进行了系列数值试验，进一步验证了算法A的有效性。

使用不同的并行压力稳定化方法，即基于两个Gauss积分的压力稳定化方法(Parallel Gauss method)、压力投影的Petrov-Galerkin方法(Parallel PSPG method)、流线迎风Petrov-Galerkin方法(Parallel SUPG method)、Galerkin最小二乘法(Parallel GLS method),我们将算法用于模拟二维方腔驱动流，图6给出了雷诺数Re=400时所得数值结果与文献中已有结果的比较，验证了并行算法的有效性。

图3 Re=800时后台阶流数值结果比较Fig.3 Comparison of numerical results for backward-facing step flow at Re=800

图4 后台阶流的流线Fig.4 Streamlines of backward-facing step flow

图5 后台阶流的压力等值线Fig.5 Pressure contours of backward-facing step flow

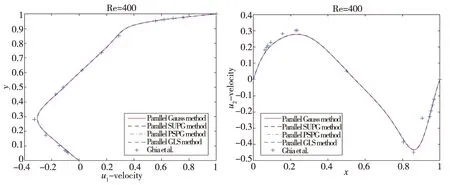
图6 方腔驱动流的并行压力稳定化方法比较Fig.6 Comparison of parallel pressure stabilization methods for lid-driven cavity flow

算例4 圆柱绕流[39]

我们使用同阶的P2-P2元和基于压力梯度投影的稳定化方法，将算法A应用于圆柱绕流的数值模拟。图7和图8显示了我们的算法将求解区域分成3子区域时的计算结果与全局串行算法所得数值结果的比较，从中可以看出我们并行算法的有效性。

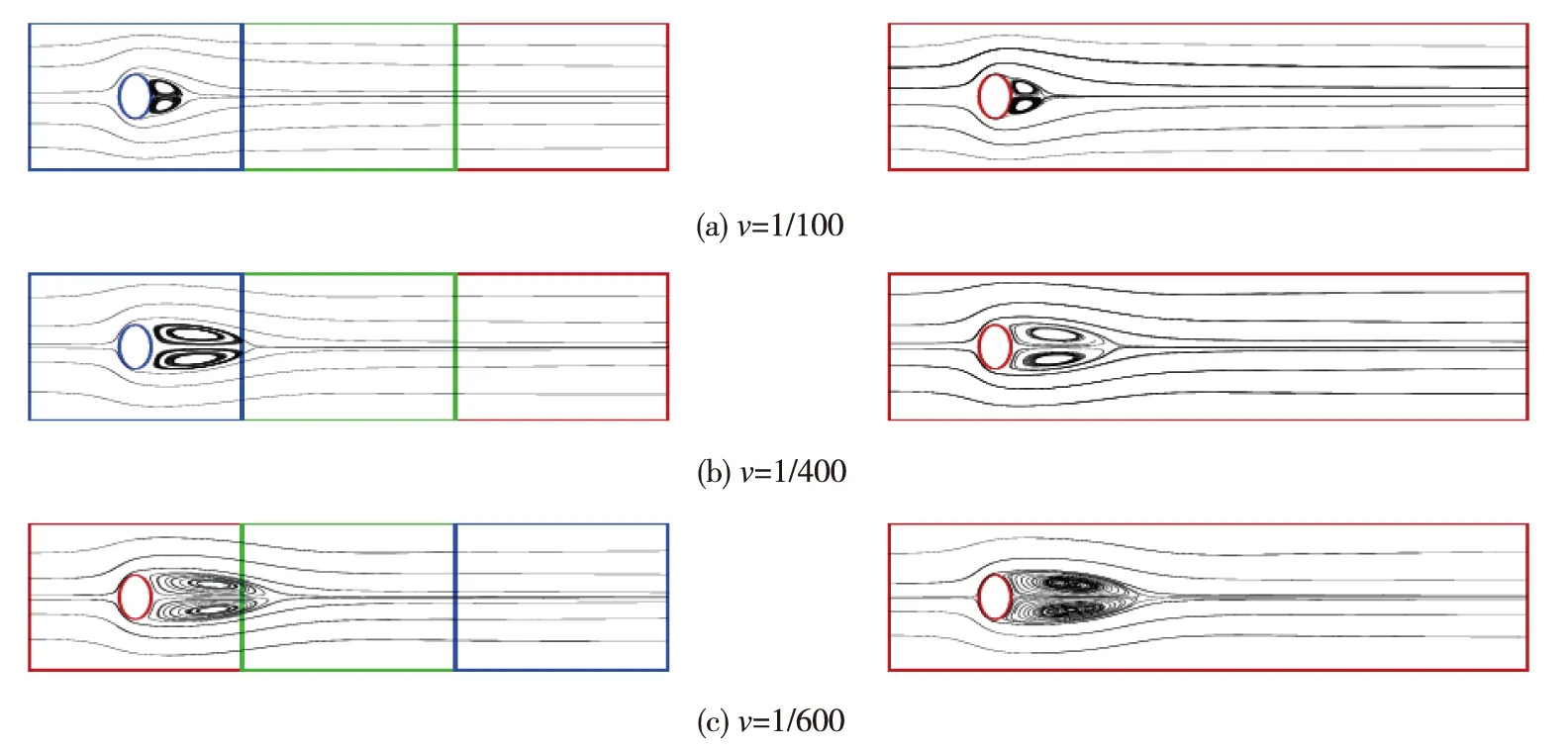
图7 圆柱绕流的流线：(左)并行算法，(右)全局串行算法Fig.7 Streamlines of flow around a circular cylinder:(left) parallel algorithm,(right) global serial algorithm

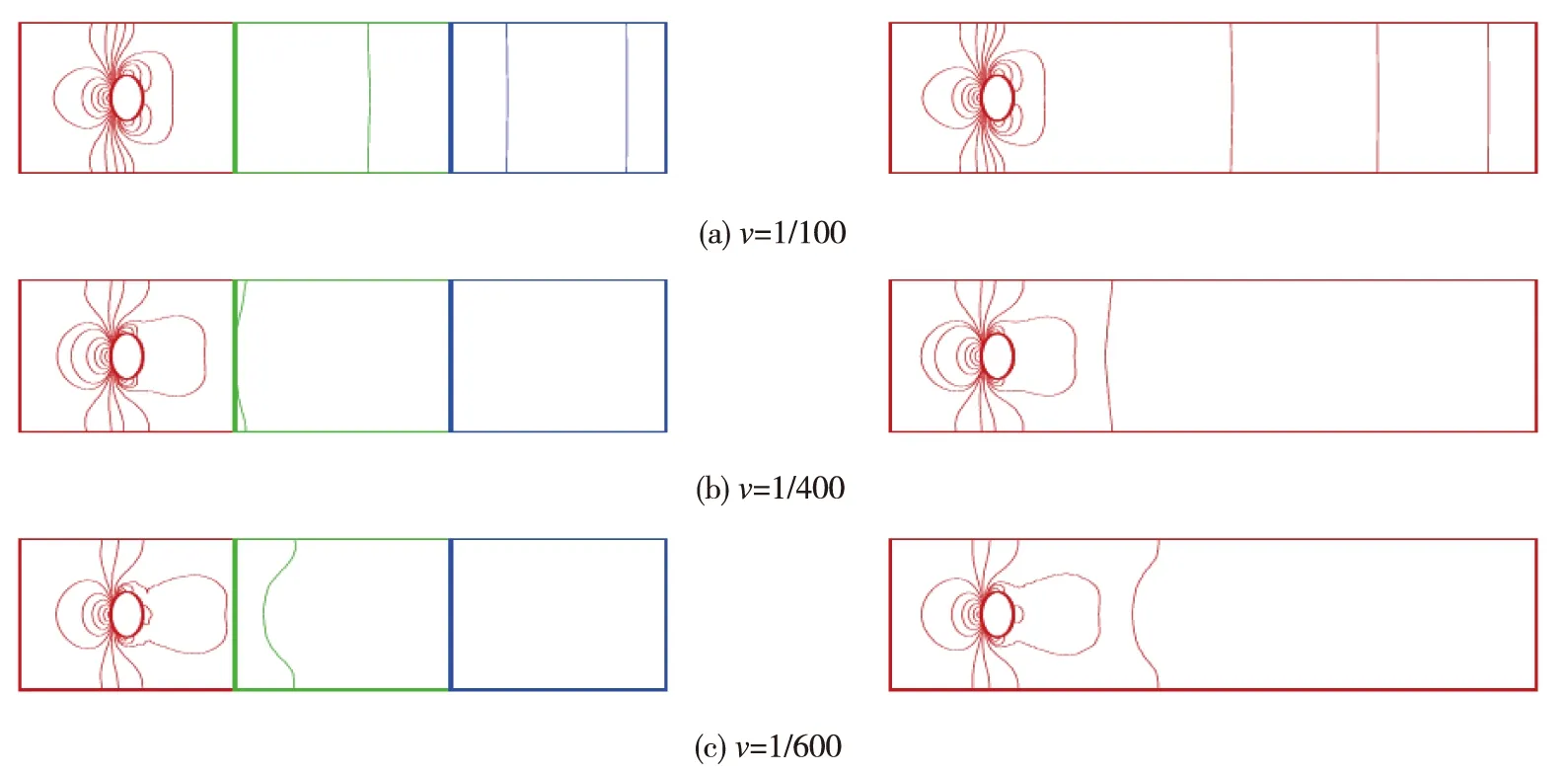
图8 圆柱绕流的压力等值线：(左)并行算法，(右)全局串行算法Fig.8 Pressure contours of flow around a circular cylinder:(left) parallel algorithm,(right) global serial algorithm

4 并行两水平有限元方法

4.1 算法描述与理论结果

将区域分解方法和两重网格离散方法相结合，我们的并行两水平有限元算法如下：

算法B1并行Oseen两水平有限元方法

3)Dj(j=1,2,…,m)中并行校正：(uh,ph)=(uH,pH)+(ej,ηj)。

上述并行算法的第二步是基于Picard迭代线性化的残差方程，我们也可采用其他线性化策略，得到类似算法：

算法B2 并行Newton两水平有限元方法

1)同算法B1。

3)同算法B1。

算法B3 并行Stokes两水平有限元方法

1)同算法B1。

3)同算法B1。

备注3.2：

2)并行算法B1-B3的第一步是在粗网格上求解，计算量很少，各处理器可相互独立地进行，因此，在整个计算过程中，处理器可相互独立地完成所有计算，从而可相互独立地选取不同的有限元空间、不同的稳定化方法、不同的线性化策略等，具有极大的灵活性；

3)与算法A类似，并行算法B1-B3中各处理器可相互独立地完成所有计算，无需交换数据，使得算法实现简单，稍加修改现有的串行程序即可实现并行计算，具有良好的并行性能。

使用inf-sup稳定的混合有限元，对于算法B1-B3所得近似解，我们有下列误差估计[35]

其中αH,αh中分别是粗细网格上关于速度稳定项的系数。上述结果表明，当

时，我们的并行算法能得到最优的收敛阶。

4.2 数值算例

算例1 解析解情形[35]

图9给出了将算法B1-B3用于求解一个已知数值解算例，不同子区域个数时的收敛阶，与理论结果一致。表3给出了与串行单水平相比，我们的并行算法使用四个子区域时所节约的计算时间。

表3 与串行单水平算法相比，并行算法所节约的时间Tab.3 Saved time by the parallel algorithms compared with the serial one-level algorithm

图9 不同区域数的并行算法收敛阶Fig.9 Convergence rates of parallel algorithms with different numbers of domains

图10子区域之间的距离对近似解精度的影响，由此可看出并行算法的健壮性。

算例2 方腔动流[35]

图11描述了将并行算法应用于雷诺数Re=10 000时的二维方腔动流且子区域个数分别为4和16个时所得的流线。图12则给出了Re=15 000和20 000时计算所得流线，这验证了我们的并行算法在大雷诺数不可压缩流数值模拟中的有效性。

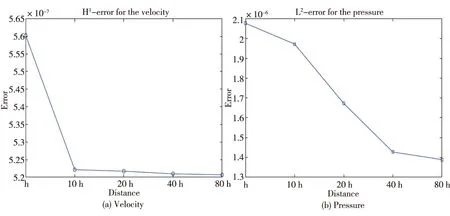
图10 子区域之间的距离对近似解精度的影响Fig.10 Influence of the distance between subdomains on the accuracy of approximate solutions

图11 方腔驱动流Re=10 000时的流线：(左)4个子区域情形，(右)16个子区域情形 Fig.11 Streamlines of lid-driven cavity flow at Re=10 000:(left) 4 subdomains,(right) 16 subdomains

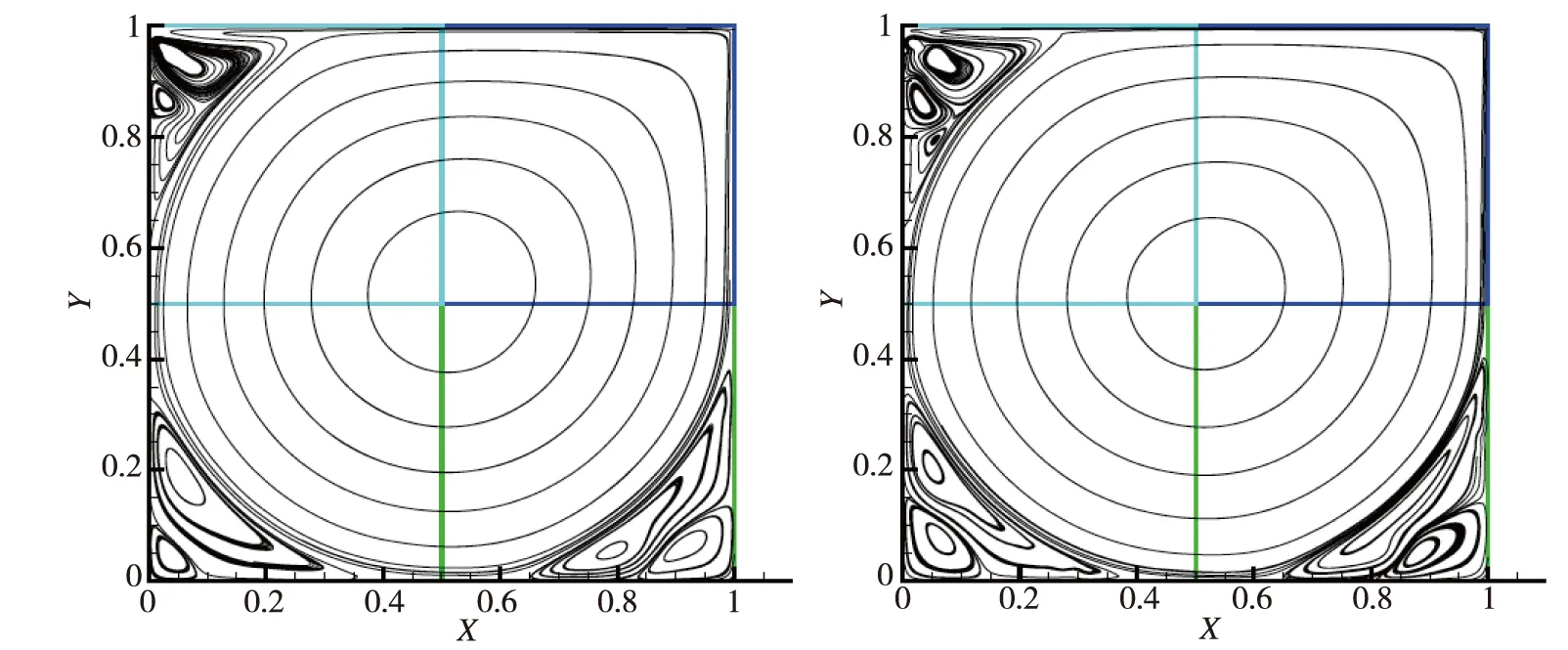
图12 方腔驱动流的流线：(左)Re=15 000，(右)Re=20 000Fig.12 Streamlines of lid-driven cavity flow:(left) Re=15 000,(right) Re=20 000

5 非线性滑移边界条件N-S方程的并行有限元算法

本节考虑带非线性滑移边界条件的N-S方程

(4)

非线性滑移边界条件的N-S方程刻画了医学和环境学领域的某些流体流动现象，如动脉硬化患者的血液流动、油在沙砾上或沙砾下的流动等。我们分别研究了非线性滑移边界条件的N-S方程并行两水平有限元算法和完全重叠型区域分解并行算法，这里仅给出完全重叠型区域分解并行算法：

算法C 非线性滑移边界条件N-S方程的完全重叠型区域分解并行算法

(Ω)(j=1,2,…,m), 使得

图13 S=0.25时分叉血液流数值结果比较：(a,b)串行有限元方法，(c,d)并行算法[40]Fig.13 Comparison of numerical results for bifurcated blood flow with S=0.25:(a,b) serial finite element method,(c,d) parallel algorithm[40]

图14 S=0.25时分叉血液流数值结果比较:(a,b) 串行有限元方法，(c,d)并行算法Fig.14 Comparison of numerical results for bifurcated blood flow with S=0.5:(a,b) serial finite element method,(c,d) parallel algorithm

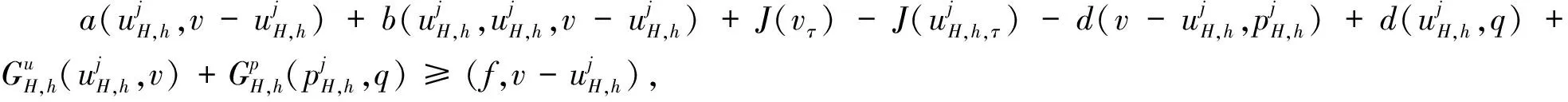
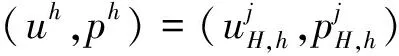
6 结束语

随着高性能并行机的发展和多核处理器的普及，高性能并行计算成为当前科学计算的主流方向。并行算法在高性能并行计算扮演着非常重要的基础作用，使得高性能并行算法的研究成为当前科学计算领域的最前沿热门课题之一。本文给出了数值求解定常不可压N-S方程的若干并行算法，这些算法分别采用完全重叠型区域分解和并行两重网格离散技巧，实现简单，稍加修改现有的串行程序即可实现并行计算，通信需求少，具有良好的并行性能，能快速有效地模拟复杂的流体流动行为，具有较广阔的应用前景。下一步的工作是并行后处理方法及非定常问题的高效并行算法。