Fe和Ni丰质子同位素中同位旋矢量巨偶极共振

刘 玲, 刘 帅, 曹李刚

(1. 沈阳师范大学 物理科学与技术学院, 沈阳 110034;2. 华北电力大学 数理学院, 北京 102206)

1937年,人们首次在光核反应实验中观察到反应截面的急剧增强,后来又在实验中观察到了反应截面迅速上升的现象,发现在15～20 MeV的能区处,反应截面急剧上升,靶核对入射光子表现出了强烈的吸收特征,后来这种现象被解释为是由原子核集体运动的激发引起的,即光子激发引起了巨偶极共振(giant dipole resonance)。而在实验上系统研究GDR,是在1975年由Berman和Fultz[1]率先进行的;对于GDR的理论研究,则已经在20世纪40年代就开始了。最近,包括相对论与非相对论方法的完全自洽的能量密度泛函理论成功地解释了巨共振的各种性质,并与相应的实验数据良好地吻合[2-6]。

现如今,人们对于巨共振的研究也逐渐发展到不稳定核中,并且在丰中子核的低能区域中发现了一个新的偶极激发矮共振(PDR)。在丰中子核中的PDR被人们解释为过剩中子对质子中子饱和核的振动。不稳定核中的PDR的存在,在核天体物理领域有着非常大的作用,在最近的理论研究中发现,PDR可以影响中子俘获反应截面,进而影响核合成和恒星中元素的丰度分布[7-8]。此外,PDR虽然只占据了经典的Thomas-Reiche-Kuhn(TRK)求和规则的很小部分,但在理论上人们发现了中子皮与能量加权求和规则之间存在一个显著线性关联,并且发现PDR的强度可以用于束缚丰中子核的中子皮以及对称能的密度依赖性[9]。在实验上,测定了O20.22,Ne26,Ni68,Sn130.132等弱束缚丰中子核中PDR的强度分布,其结果也被不同的实验组所验证。

另外,在一些丰质子核中的质子皮的结构已经被预先预测,在实验上也观察到带有质子晕或者质子皮的核[10]。对于丰质子核研究可以增加人们对于强相互作用的理解,可以研究新的放射形式,同时也是天体核物理中研究核合成过程的关键。比如使用X射线的快速质子捕获过程。但是实验上丰质子核只出现在Z≪50的核中,因为库仑斥力的存在,质子滴线更加接近β稳定线,带有质子晕的核只可能出现轻元素中。由于这些原因,使得丰质子中的PDR看起来并不存在,而且在过去的实验中并没有观察到丰质子的PDR现象,靠近质子滴线的核子的偶极激发方面的研究也很少[11-15]。不过,随着世界上新的实验装置的建造(比如我国的HIAF[16]),相信在不远的将来,丰质子核中的PDR现象也会被测量出来。

本文在完全自洽的环境下研究了Fe和Ni丰质子同位素的偶极激发性质,使用Skyrme Hartree-Fock结合BCS近似的方法研究这些核子的基态性质,使用QRPA(准粒子无规位相近似)的方法研究偶极激发性质。对于Fe和Ni的PDR性质,本文使用Skyrme HF+BCS方法计算并且分析了它们的激发能、跃迁密度、以及集体性等一系列性质。

1 理论框架

对于Skyrme相互作用的标准形式,本文采用与文献[17]中相同的符号,在原子核中的2个核子的空间、自旋和同位旋riσiτi通过零力程相互作用,速度、密度依赖的Skyrme相互作用标准形式为

为解决势场中的对力相互作用,本文使用BCS模型进行修正,修正公式为

其中:ρ(r)为粒子密度;ρ0为0.16fm-3;η取0.5。

在所给出的标准形式下,核子系统的总能量可以通过对Skyme密度泛函的积分给出,公式如下

在Skyrme HF+BCS近似条件下,准粒子波函数和与它相对应的能量可以通过下面自洽的方程得到

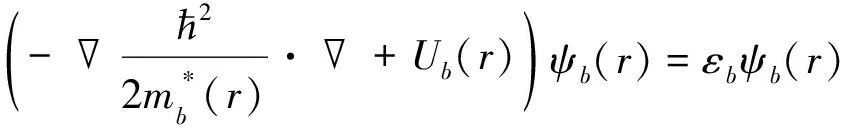
通过求解HF+BCS方程,可以得到单粒子的能级和质子中子的波函数。基于基态的计算,可以为QRPA计算建立2qp构型。在QRPA方法[18]中体系矩阵方程形式为

这里:Eb为第b个激发态的激发能;XbYb是前向与后向跃迁振幅。计算QRPA中的偶极强度为

μ和b为粒子所处在的能级。对于同位旋矢量巨偶极共振,外场算符为

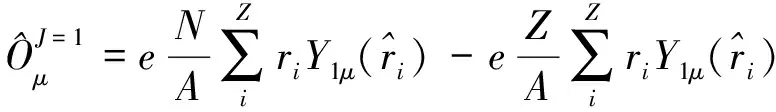
将计算的离散数据通过洛伦兹函数进行处理得

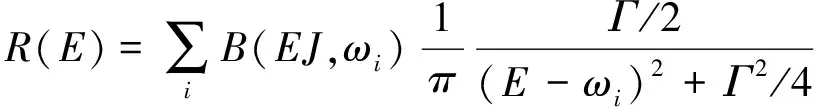
此处的洛伦兹函数展开宽度Γ=1 MeV。求解QRPA方程后,定义了求和规则如下

2 结果与讨论

首先使用Skyrme HF-BCS的方法计算了Fe和Ni的丰质子同位素的基态性质,假设所选取的核子的都为球形,所有计算都在一个半径为16fm的坐标空间中完成的,本文选用Skyrme相互作用中的Sly5的参数。在表1中展示了所计算的Fe与Ni元素丰质子同位素的总结合能等数据,本文发现所预测的核子的总结合能比实验数据要大3～6 MeV,在弱结合能中质子中子的费米能非常接近于0,表1中可以看到本文所计算的Fe和Ni的丰质子同位素的质子费米能非常接近0,甚至有一些是负的,这也意味着这些核子非常的不稳定,极易发生β+衰变。图1是丰质子核Fe和Ni的质子中子的密度分布图像,在图中可以清楚的看到,在这些丰质子核子中质子的密度分布较与中子的密度分布向外扩展了很多,同时本文中所预测的均方根半径也要比中子的均方根半径大很多,特别是在44Fe和46Ni中,这种情况也意味着在这些核子中可能会有质子晕或者质子皮的结构存在。

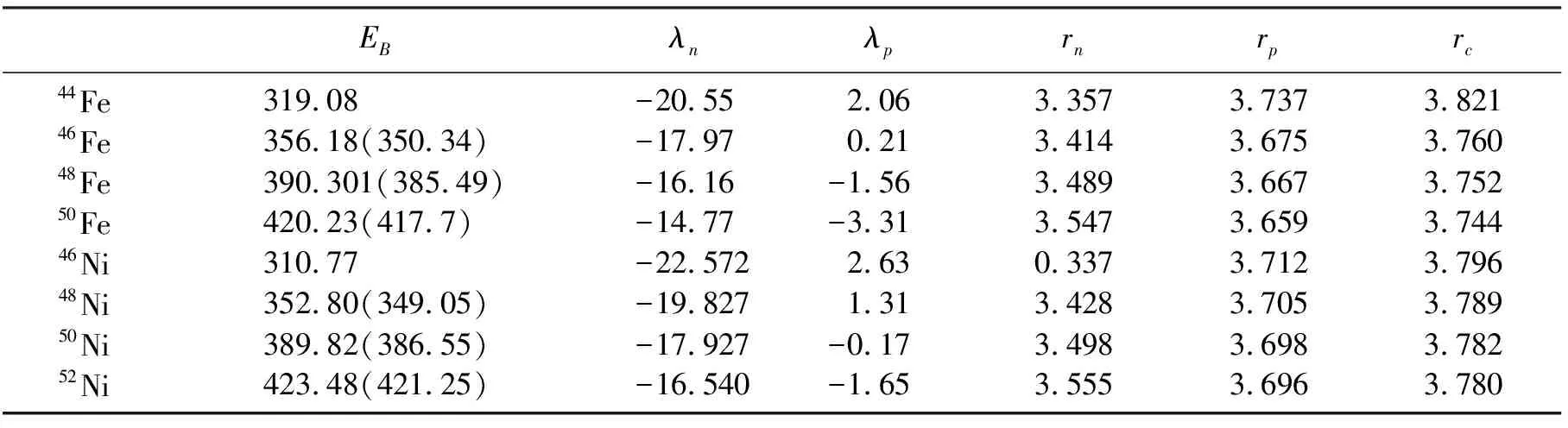
表1 Fe和Ni丰质子同位素元素基态性质的计算结果,包括总结和能EB,质子与中子的费米能(λn,λp),单位为MeV质子和中子的均方根半径(rn,rp),以及电荷半径(rc)。单位为fm

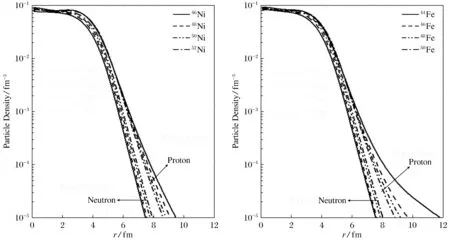
图1 Fe和Ni的丰质子同位素链的密度分布图像Fig.1 Neutron and proton density distributions in proton-rich Ni and Fe isotopes

为了得到Fe和Ni的丰质子同位素的偶极子激发,需要求解基于Skyrme HF+BCS基态的QRPA方程。对此采用无限深球面势阱的方法来求解Skyrme HF+BCS,势阱的半径为16fm。在球形深势阱坐标空间中解决完HF+BCS方程后,又建立了偶极子激发的双准粒子空间构型用以解决QRPA矩阵方程。本文使用Sly5相互作用以完全自洽的方式进行QRPA的计算[17],并没有对剩余相互作用进行近似处理,因为计算中使用的所有项与基态计算中使用的相同,剩余相互作用的具体细节可在文献[13]中查看。

图2中,展示了所计算的Fe(a,b,c,d)和Ni(e,f,g,h)的丰质子同位素的同位旋矢量偶极激发强度分布(图中的实线),对于QRPA计算结果中离散的数据,本文使用洛伦兹展开进行模糊处理,Lorentzian宽度为1 MeV。在丰质子的Fe和Ni的同位素的同位旋矢量的偶极激发图像中,可以在17 MeV附近看到一个明显的峰,这符合正常的GDR。而在小于10 MeV的能量区域内,在一些核子(比如Fe,Ni)的图像上出现矮小一点的峰,这些值得注意的矮小的峰也就是之前所说的不稳定核中的矮偶极共振。在表2中又给出了用QRPA计算的丰质子Fe和Ni同位素的偶极子强度的能量(非能量)加权求和规则m1m0将能量分为2个区域,低能区(0≤E≤10)和高能区(10≤E≤30),PDR主要分布在低能区,GDR主要分布在高能区。在表中同样给出了经典的TRK求和规则。从表2中可以清楚的看出,PDR部分的能量(非能量)加权求和规则是随着同位素链的质量数的增加而减少的。PDR的能量加权求和规则约占经典的TRK求和规则的0.3%～0.4%,而对于GDR,能量(非能量)加权求和规则m0m1在每个同位素链中都随着核质量数的增加而增加,这与之前在PDR中发现的情况相反。并且这些核子GDR的能量加权求和规则比TRK求和规则还要大。

表2 QRPA计算中Fe和Ni的丰质子同位素的有无能量加权求和规则m1,m0,单位分别为(e2fmMeV)与(e2fm),最后一列为经典TRK求和规则的值,单位为(e2fmMeV)

图2 Ni和Fe丰质子同位素同位旋矢量偶极共振响应方程,Lorentzian宽度为1 MeV

计算所得到的PDR(能量小于10 MeV或者在10 MeV附近)和GDR(能量大于15 MeV)的质子中子的跃迁密度分别如图所示图3,从PDR的图中可以看出,在核内部质子中子的跃迁密度是同向的,而在核的表皮处则主要是质子振动,这是典型的丰质子核中的矮共振现象,同时也表明了这个PDR具有同位旋标量的特性。类似的性质已经在一些丰中子核的研究中被发现了[19-23]。而GDR的中子质子的跃迁密度是反相位的。这是典型的同位旋矢量巨偶极共振的形式。

对于给定激发态b的质子和中子的2qp构型的QRPA振幅可以表示为

归一化条件为

对于Fe和Ni的丰质子同位素,在表3中给出了给定激发态下质子和中子2qp构型的最大的QRPA振幅。通过表3中的数据可看出,对于Fe和Ni的丰质子同位素的GDR态,有超过10个的2qp

表3在Fe和Ni的丰质子同位素的激发态中质子中子的2qp构型的QRPA振幅
Table 3The largest QRPA amplitudes of proton and neutron 2qp configurations for a given excited state in the proton-rich Fe and Ni isotopes

图3 46,48,50Ni的44,46,48FePDR态和GDR态的质子、中子跃迁密度分布

3 总 结

综上所述,本文以完全自洽的方法系统地研究了Fe和Ni丰质子同位素的同位旋矢量巨偶极共振的性质。用Skyrme Hartree Fock加上BCS近似的方法并且在计算过程中使用了SLy5 Skyrme相互作用和密度依赖的对相互作用,得到了上述元素的基态结合能以及质子中子的均方根半径和电荷半径。结果表明,通过本文的计算,在丰质子Fe和Ni中发现了明显的质子晕(皮)结构。并且利用本文的理论模型可以再现这些原子核的实验电荷半径。对于所计算的丰质子核的偶极激发态性质,本文使用准粒子无规位相近似的方法来进行计算。在每一个核子的响应方程的图像中,可以在17 MeV附近发现一个明显的巨偶极共振,通过相应的跃迁密度图像可以看出,它的中子和质子的跃迁密度是反相位的,可以看出这些偶极共振是典型的同位旋矢量巨偶极共振。

除了这些巨偶极共振之外,还有一些低强度的共振分布在10 MeV以下的能量区域。它们的强度相对于巨偶极共振要弱一些,这些共振就是矮偶极共振。并且靠近质子滴线的核子的能量加权求和规则约占据TRK求和规则的4%左右,随着同位素链中元素的质量数的增加,这个值在逐渐的减小,甚至在Fe50和Ni52中时占比几乎接近于0。矮共振的跃迁密度分布图像表明,质子和中子在核子内部的运动是同相的,而核子的晕主要是质子运动造成的,这也意味着矮共振具有同位旋标量特性。通过分析矮共振状态下质子和中子2qp构型的QRPA振幅数据,本文发现PDR状态的QRPA振幅,像是单个的2qp激发,一个或两个的2qp激发能够占据总QRPA振幅的99%。得出的结论是,Fe和Ni元素的矮共振激发不是由多个单粒子激发构成的,不具有明显的集体性。