特高压长悬臂输电塔结构风振扭转响应

张骞，叶震，蔡建国，余亮，冯健

(1. 东南大学混凝土及预应力混凝土结构教育部重点实验室，江苏南京，210096；2. 华东建筑设计研究总院，上海，200002；3. 江苏省电力设计院，江苏南京，211102)

特高压直流输电线路因输送容量大和距离远等突出优势逐渐得到广泛关注，但是由于线路承担电压等级较高、电气间隙较大，对结构体系的设计提出了更高要求，需要输电塔高度更高、横担更长、承担荷载更大。目前，在±800 kV特高压直流输电线路的研究基础上，国内外已经开展±1 100 kV 特高压输电线路的研究。对于输电塔结构，风荷载是结构破坏的主要因素[1]，已经逐步开展风振响应特性的仿真时程分析[2-4]和风洞试验研究[5-9]，但是由于±1 100 kV 特高压直流输电塔的结构形式出现较晚，学者很少研究该结构体系的风振响应特性。±1 100 kV 特高压直流输电塔结构相对于普通的输电塔结构最突出的特点是横担较长，结构的一阶振型模式不再是平面内的弯曲而是整体扭转，目前针对输电塔横担部分的风振响应的研究也较少。夏亮等[10-12]通过对长横担输电塔的风洞试验，发现在脉动风作用下塔身发生整体弯曲振动，同时塔头发生明显的扭转振动，而且横担处的加速度响应明显大于塔身相同高度处的响应。聂建波等[13]通过对±800 kV 特高压T 型长横担输电塔进行时域法和频遇法分析，指出横担部位的风振系数约为等高度塔身部位风振系数的1.3倍。目前，输电塔结构的风致扭转效应研究较少，而且国内对高层建筑的风致扭转效应的研究方式主要为风洞试验[14-17]，分析结果过度依赖于建筑结构形式，不具有普遍适用性。LIANG 等[18]针对于高层建筑提出的扭转风荷载计算方法过于简化、误差较大，不足以推广应用。对于特高压直流输电塔结构，由于长悬臂的特点，风致扭转效应将对结构产生较大的不利影响，不可忽略。为此，本文作者首先分析了风荷载作用下长悬臂输电塔结构产生扭转响应的原因；然后，采用有限元动力时程分析方法计算特高压长悬臂输电塔的风振响应；最后，采用等效扭转风振系数的方法分析扭转效应对结构内力的影响，并研究风向角和输电塔横担总长度对结构扭转效应的影响。

1 长悬臂输电塔风振扭转响应

对于对称的长悬臂输电塔结构，可以采用如图1所示的简化模型进行概念设计分析，其中，塔高为H，横担总长为2L，风荷载施加在等效的质量点上。

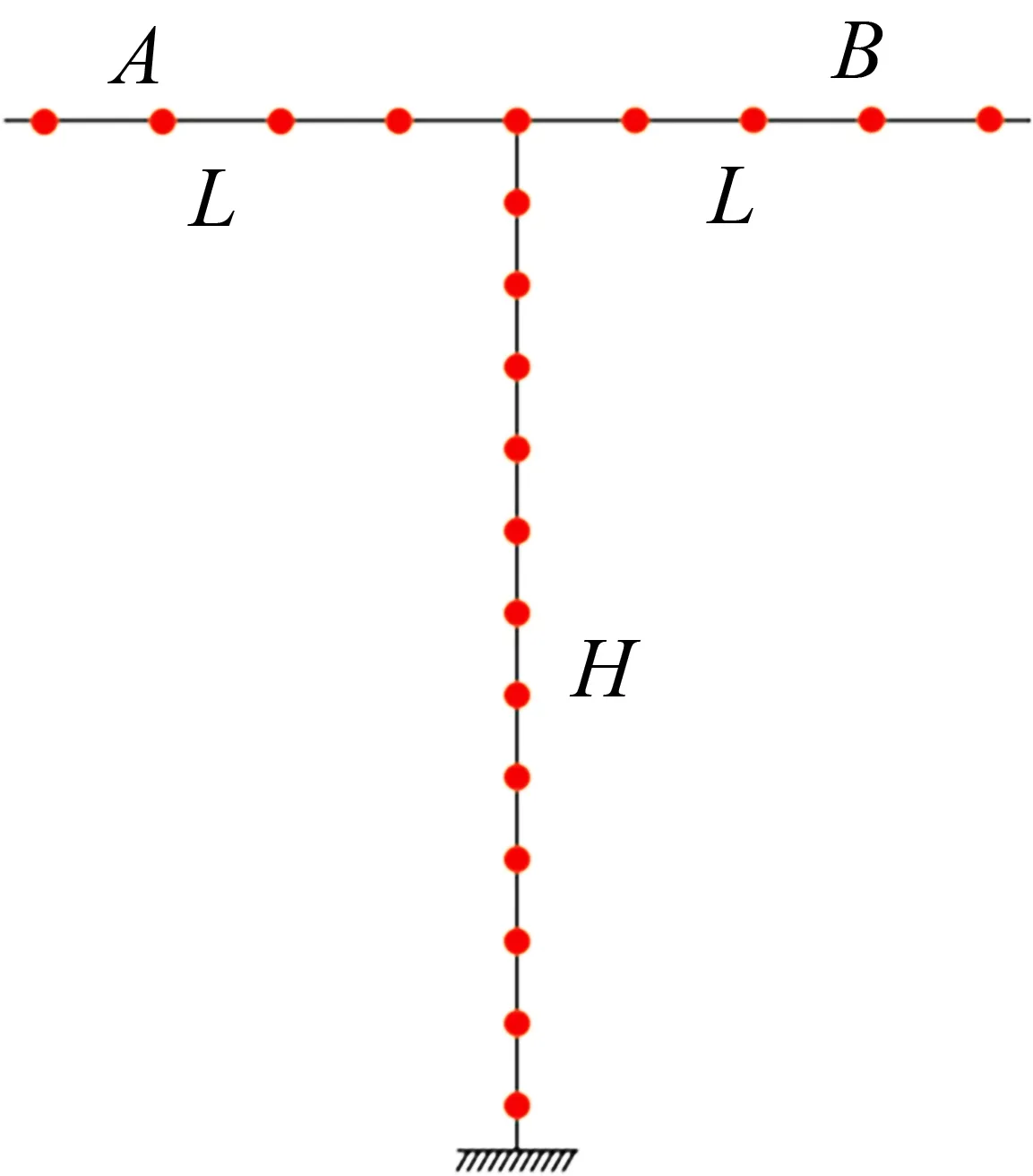
图1 长悬臂输电塔概念分析模型Fig.1 Conceptual analysis model of the long cantilever transmission tower

目前对长悬臂输电塔结构尚未有成熟的设计分析方法，本文采用动力时程法分析风荷载作用下输电塔结构的动力响应。采用多维的自回归模型(VAR 模型)结合风速谱模拟输电塔结构的脉动风[19]，M个空间相关点脉动风速时间序列V(x,y,z,t)的VAR模型为

式中：p为VAR 模型的阶数；k=1，2，…，p；ψk为VAR模型的M×M阶自回归系数矩阵；Δt为时间步长；N(t)为独立随机过程向量。

对于多维平稳时间序列模型，横担上左右两侧对称点的风速时程由于空间位置的相干性，不再保持一致，横担上左右对称点A与B的风速时间序列的协方差矩阵R(kΔt)可以通过功率谱密度函数结合维纳—辛钦公式得到

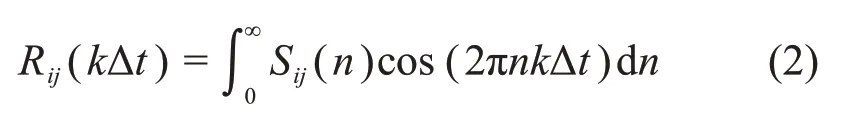
式中：n为脉动风频率；i和j分别为节点A和B的；Sij(n)在i=j时为自功率谱密度函数，在i≠j时为互功率谱密度函数，两者之间的关系为

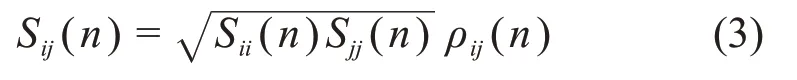
式中：ρij(n)为空间位置的相关函数，可以表示为

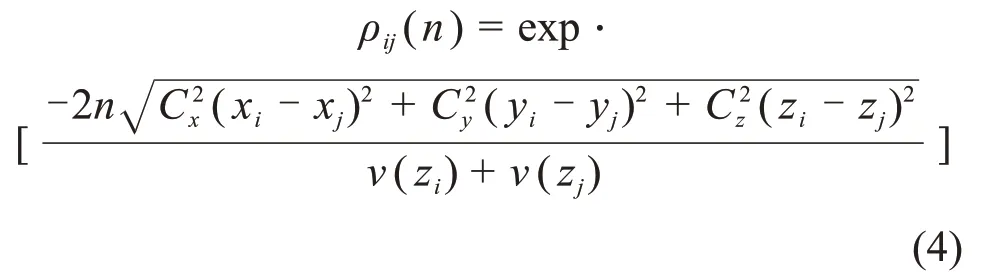
式中：Cx，Cy和Cz分别为空间任意2点x，y和z方向的指数衰减系数，取值分别为8，16和10；v(zi)和v(zj)分别为i和j这2点对应的平均风速。

由上述分析可知，对称点A与B同一时刻的协方差矩阵R(0)为

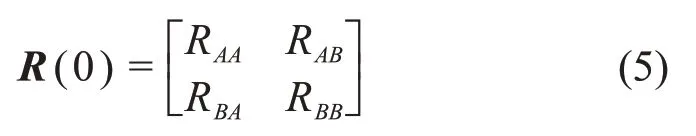
对称点A与B相同时刻的风速序列的相关系数λAB为

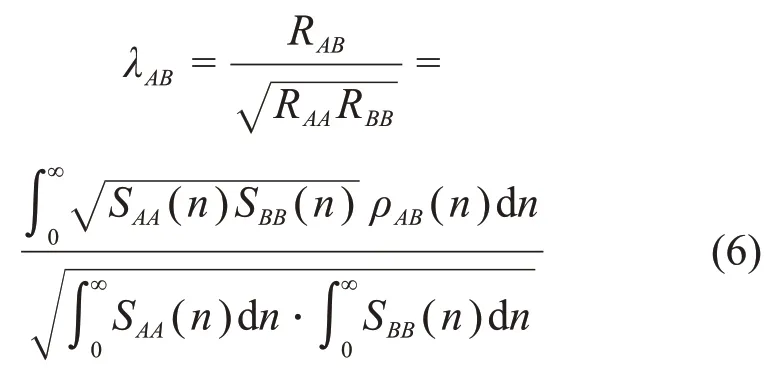
结合式(6)和式(4)可以发现：对称点A和B的风速时间序列非对称，且随着A与B之间的距离增大，两者之间的相关性减弱，对称点的风压时程和风荷载时程也不一样，因此，即使作用在对称的长悬臂输电塔结构上，经过动力计算后也会产生非对称的响应，即扭转响应，而目前在以风振系数为基础的拟静力风振响应计算中并没有考虑到这种响应。

为了便于分析影响结构扭转响应的因素，将对称的长悬臂输电塔模型进行等效，横担的等效截面惯性矩为I，弹性模量为E，将塔身部分等效为一个扭转弹簧，刚度为kT，如图2所示。

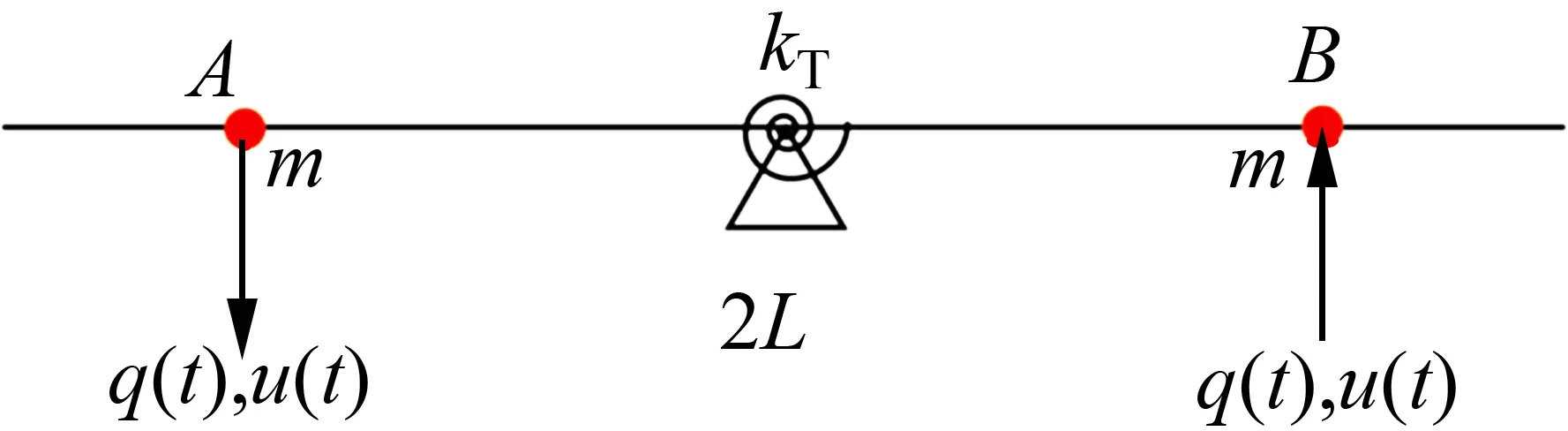
图2 横担扭转分析模型Fig.2 Analysis model of cross arm torsion

将对称点的风荷载分解成对称部分和反对称部分，扭转响应主要由反对称部分产生，根据风速的模拟过程可知，反对称荷载时程的期望E(q(t))=0。考虑到结构的对称性，并将结构质量对称等效在点A和B上，则该单自由度体系的动力学方程和相应的等效刚度分别为

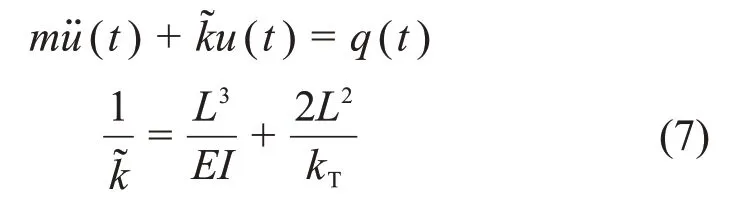
式中：m为等效质点质量；u(t)，q(t)和分别为等效质点A与B的位移时程、荷载时程和加速度时程。

根据Duhamel积分的离散形式，可知横担结构产生扭转的位移为

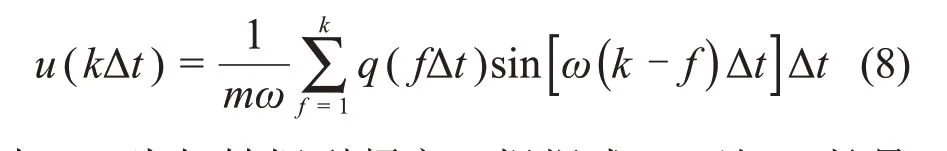
式中：ω为扭转振型频率。根据式(8)可知：长悬臂输电塔结构的扭转效应与横担总长度、横担高度、结构质量分布和结构基频等因素相关，而且这些因素相互影响，增加了分析的复杂性。

2 长悬臂输电塔风振响应特性

2.1 风振系数计算

特高压长悬臂输电塔结构模型如图3所示。塔身部分的总高度H为66.7 m，瓶口宽度为10.0 m，根开为17.2 m，横担部分总长度为69.0 m，结构总质量为184.7 t。塔身部分从下到上结构包络尺寸逐渐减小，横担部分从根部到端部结构包络尺寸也逐渐减小。计算风荷载的标准风速为43 m/s，场地类型为B类。

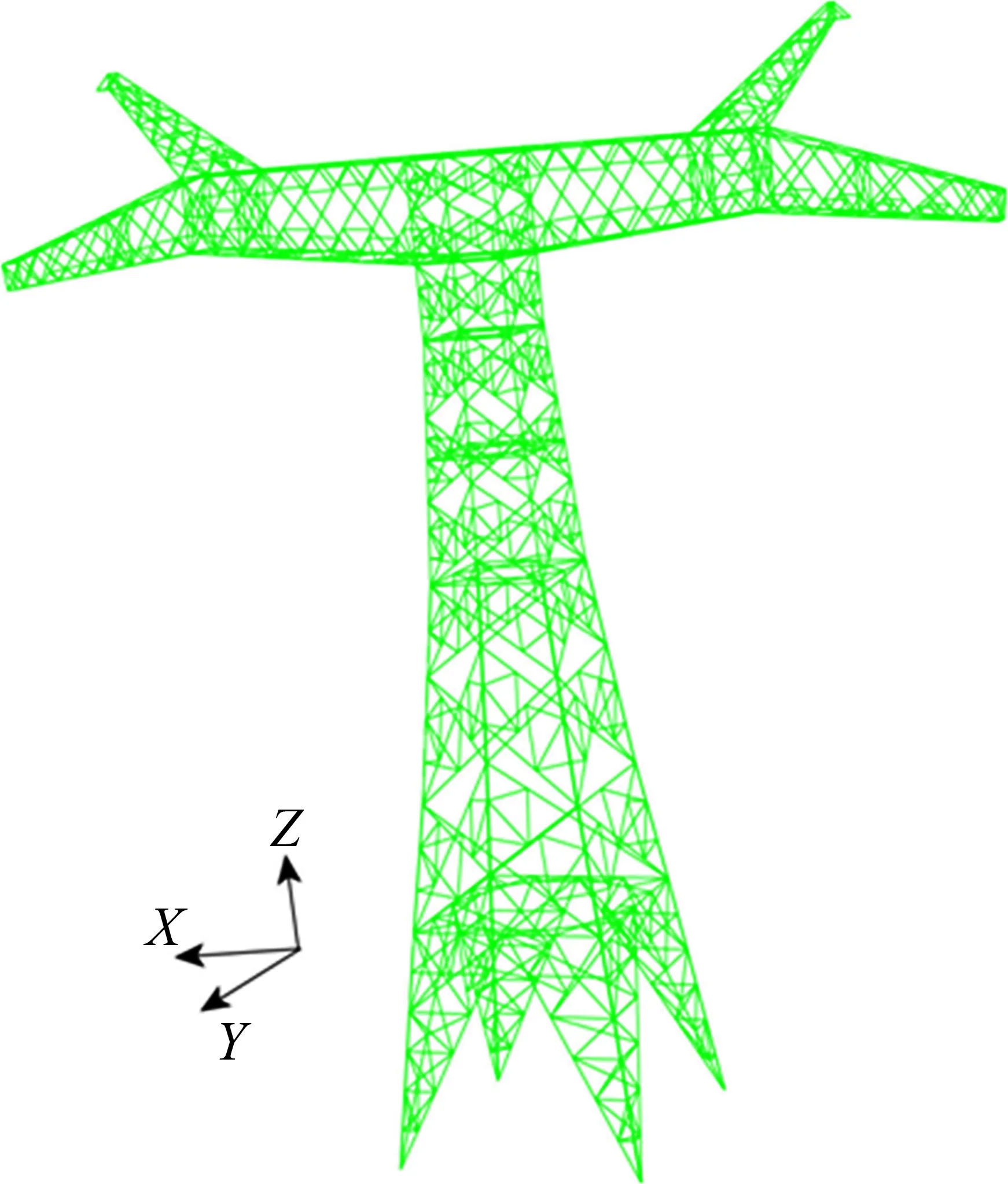
图3 输电塔结构模型Fig.3 Transmission tower model

特高压长悬臂输电塔的第1阶模态为绕Z轴扭转，如图4所示，对应频率为1.21 Hz，第2阶模态为XZ平面内弯曲，频率扭平比为1.25，而常规非长悬臂的输电塔结构的第1阶模态为平面内弯曲且频率扭平比小于0.9，两者的动力特性不一致。

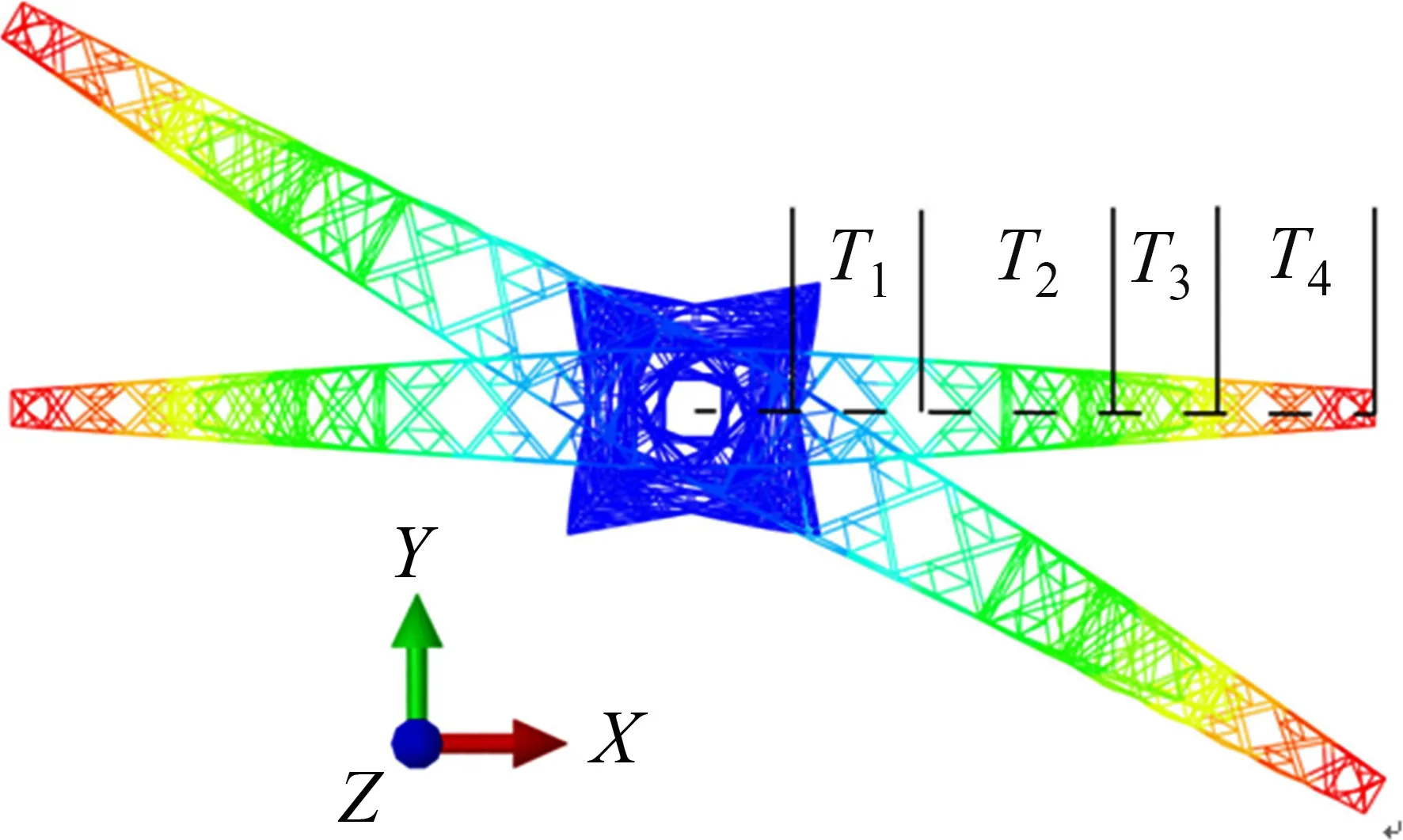
图4 长悬臂输电塔的第1阶自振模式Fig.4 First order vibration mode of long cantilever transmission tower

对长悬臂输电塔结构进行风振分析时，忽略输电线的影响。首先，将输电塔的塔身和横担分别沿高度和宽度进行区间划分，采用VAR 法结合Davenport 风速谱模拟得到区间内计算点的风速时程，其中模拟风速的总时间为2 000 s，时间间隔Δt为0.1 s，VAR模型阶数p为4。将模拟得到风速时程转化为节点风荷载时程，采用ABAQUS 分析长悬臂输电塔风荷载动力时程，得到节点的位移响应时程。然后，计算各区间的位移响应均方根。考虑结构阻尼，动力时程分析采用瑞利阻尼系数，根据结构前两阶频率计算得到的质量系数和刚度系数分别为0.2和0.002。横担区间的位移响应由于塔身弯曲、塔身扭转和横担弯曲3部分组成。由于横担本身不存在扭转变形，可以根据文献[20]得到各区段的风振系数，如表1所示，其中，横担两侧对称位置的风振系数一致。由表1可见：整体上随着与横担中心的距离增大，对应的风振系数增大。

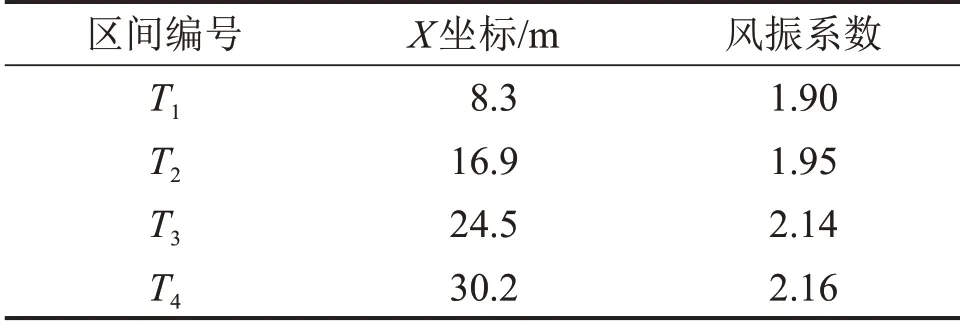
表1 横担各区间中心处计算风振系数Table 1 Wind vibration coefficient in the center of cross arm sections

2.2 扭转效应分析

对称长悬臂输电塔结构在非一致风荷载作用下，横担会产生扭转变形，在风荷载时程作用下，长悬臂输电塔横担各对称点(A，B，C和D)相对于横担中心处O(塔身顶部)的Y方向位移时程(UAO，UBO，UCO和UDO顺风方向)如图5所示。

整个时程范围内(0～2 000 s)位移时程的规律一致，为便于说明只选取80～100 s位移时程曲线，其中，UO表示横担中心处Y方向的位移。

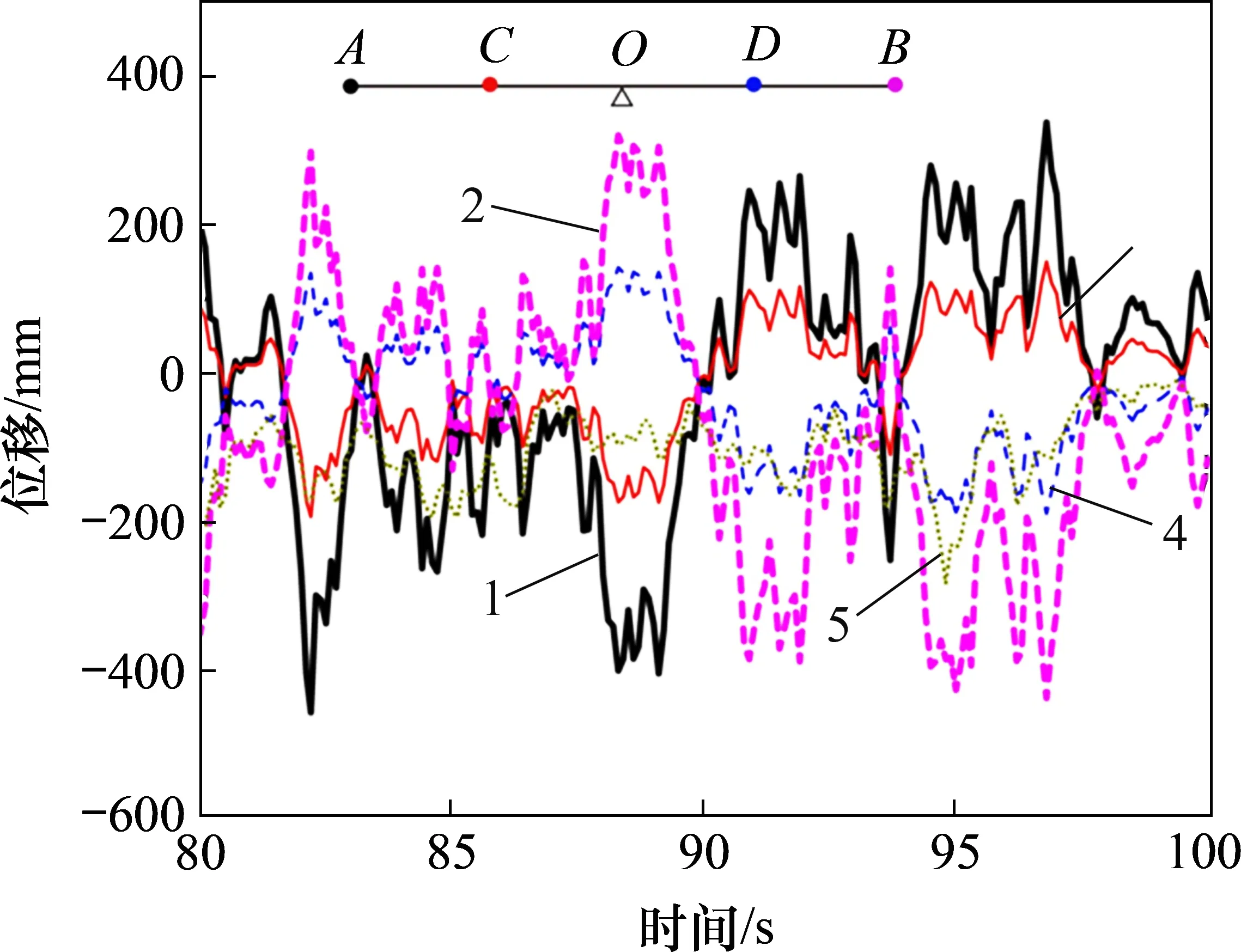
图5 横担上部分对称点的位移时程曲线Fig.5 Displacement time history curves of some symmetrical points on the cross arm

根据图5可知：横担上对称点相对于中心点的位移虽然随着时间不断变化，但是呈现出近似反对称的规律，且横担Y方向上的相对位移相对于中心点处的实际位移较大，表明横担绕中心点发生的整体扭转变形较大，扭转为横担的主要变形模式。某时刻输电塔横担Y方向位移U2如图6 所示。由图6 可见：输电塔在Y方向平动的同时绕Z轴发生较大的扭转变形，而这种变形模式无法利用现有的风振系数分析方法得到。

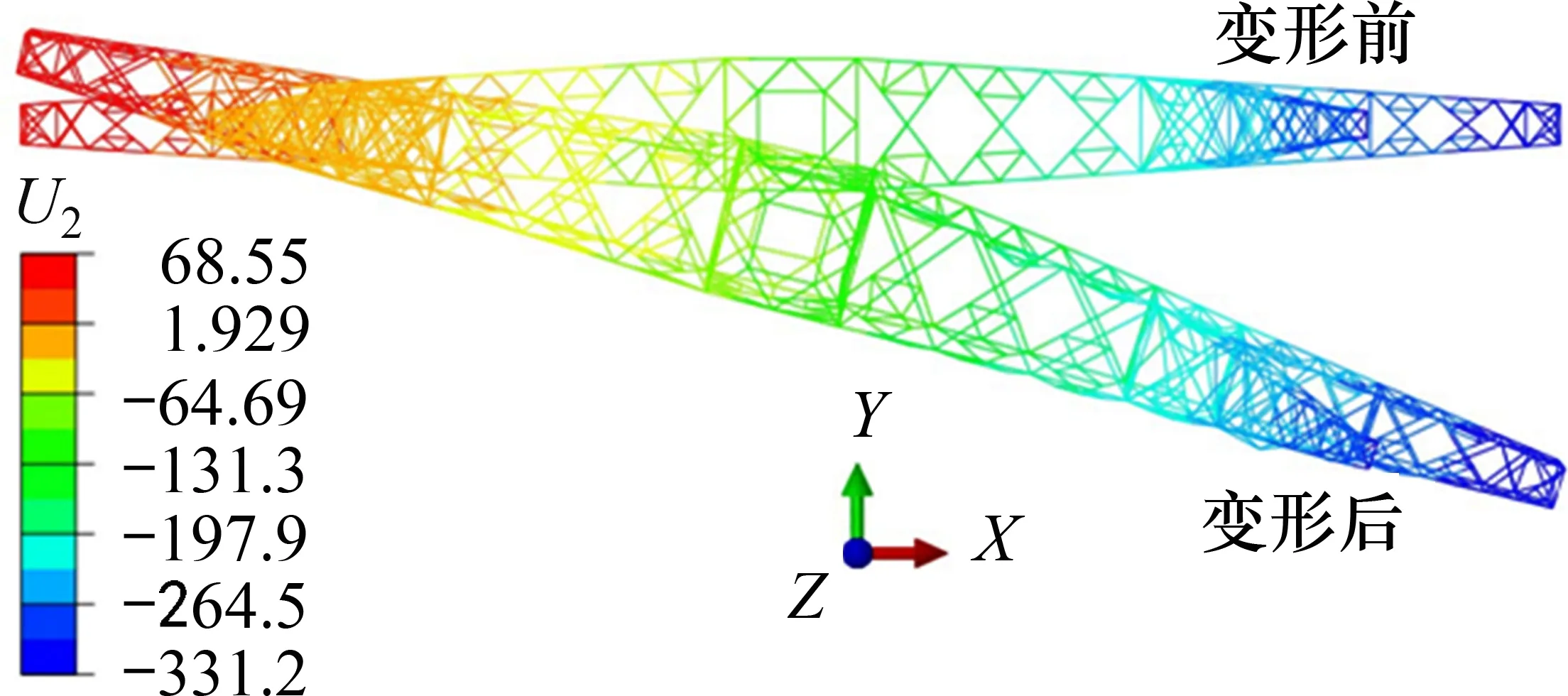
图6 某时刻横担Y方向变形示意Fig.6 Deformation sketch of the cross arm in Y direction at a certain time

考虑到动力计算结果的离散性，进行7次风荷载动力时程计算，选取结果的平均值进行分析。考虑到横担扭转的方向性，横担扭转对应的Y方向位移7次最大值的平均值沿横担方向的分布关系如图7所示。由图7可见：采用的位移平均值在横担上呈线性分布，顺时针和逆时针的拟合系数均达到0.95， 相应的转角分别为0.010 2 rad 和0.011 2 rad，采用平均值0.010 7 rad 为该长悬臂输电塔结构的扭转角，表征时程风荷载作用下横担的扭转效应。

为了在设计中考虑到输电塔结构的扭转效应，基于扭转效应等效原则在现有的风振系数计算的基础上定义等效扭转风振系数βr，保证动力时程风荷载和相应的等效扭转静力风荷载产生的横担扭转效应相同。假定横担上各处的等效扭转风振系数相同，在塔头两侧的横担上风荷载方向相反，则可以组合出顺时针扭转和逆时针扭转2种横担扭转工况。

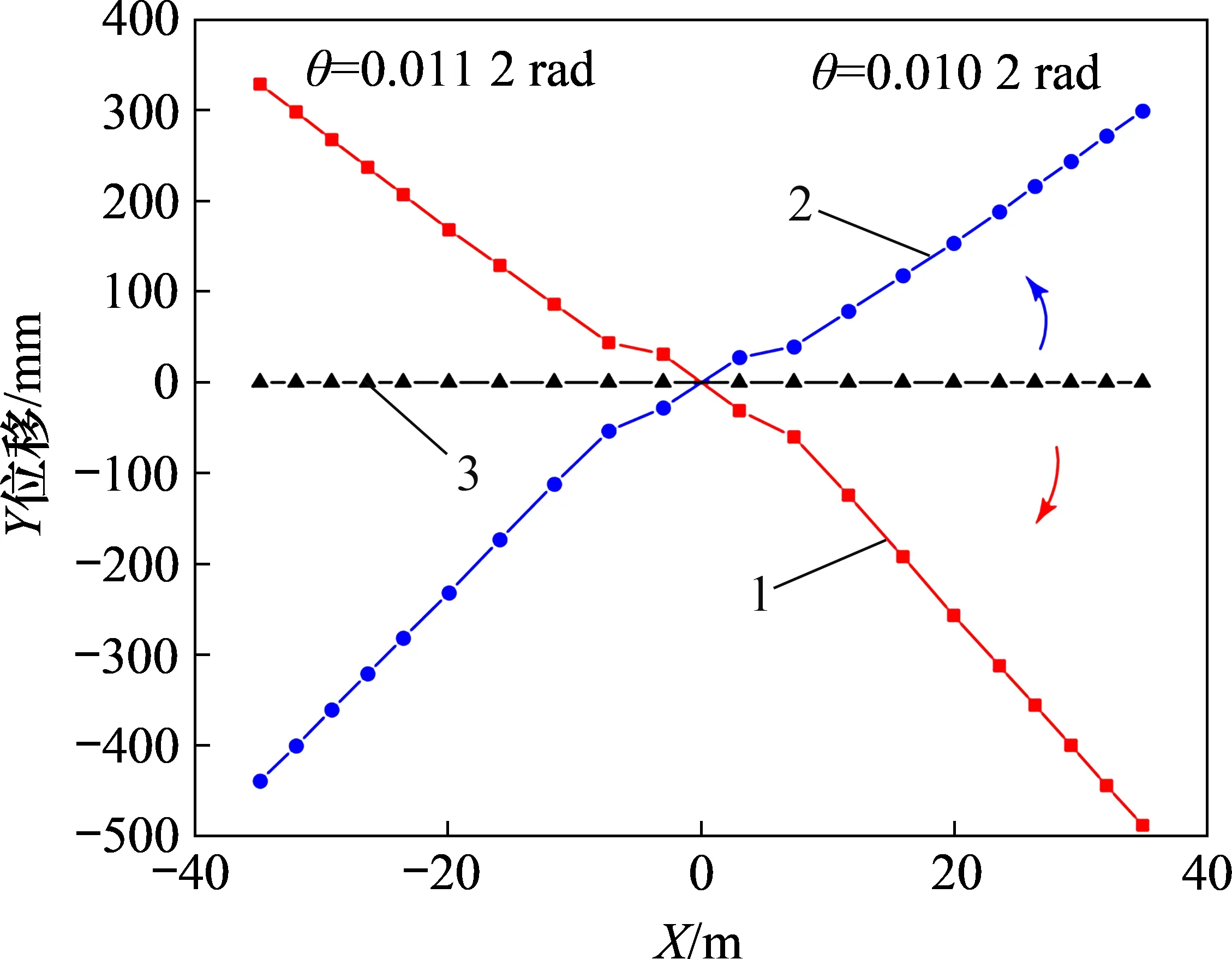
图7 时程风荷载作用下横担扭转变形Fig.7 Torsional deformation of the cross arm under time history wind load

首先，给待分析的长悬臂输电塔结构施加等效扭转风振系数为1.0时对应的扭转荷载，即按照文献[21]中风荷载计算公式得到每个节点的静风荷载；然后，将每个节点的静风荷载乘以等效扭转风振系数，并使塔头左右横担节点的静风荷载方向相反，利用ABAQUS 计算横担的扭转变形和扭转角，如图8 所示，此时的扭转角为0.014 3 rad。在等效扭转风阵系数对应的扭转荷载作用下，横担发生整体扭转变形，此时横担的扭转变形和等效的扭转风振系数之间基本为线性关系，则该长悬臂输电塔结构横担部分的等效扭转风振系数βr=0.75。

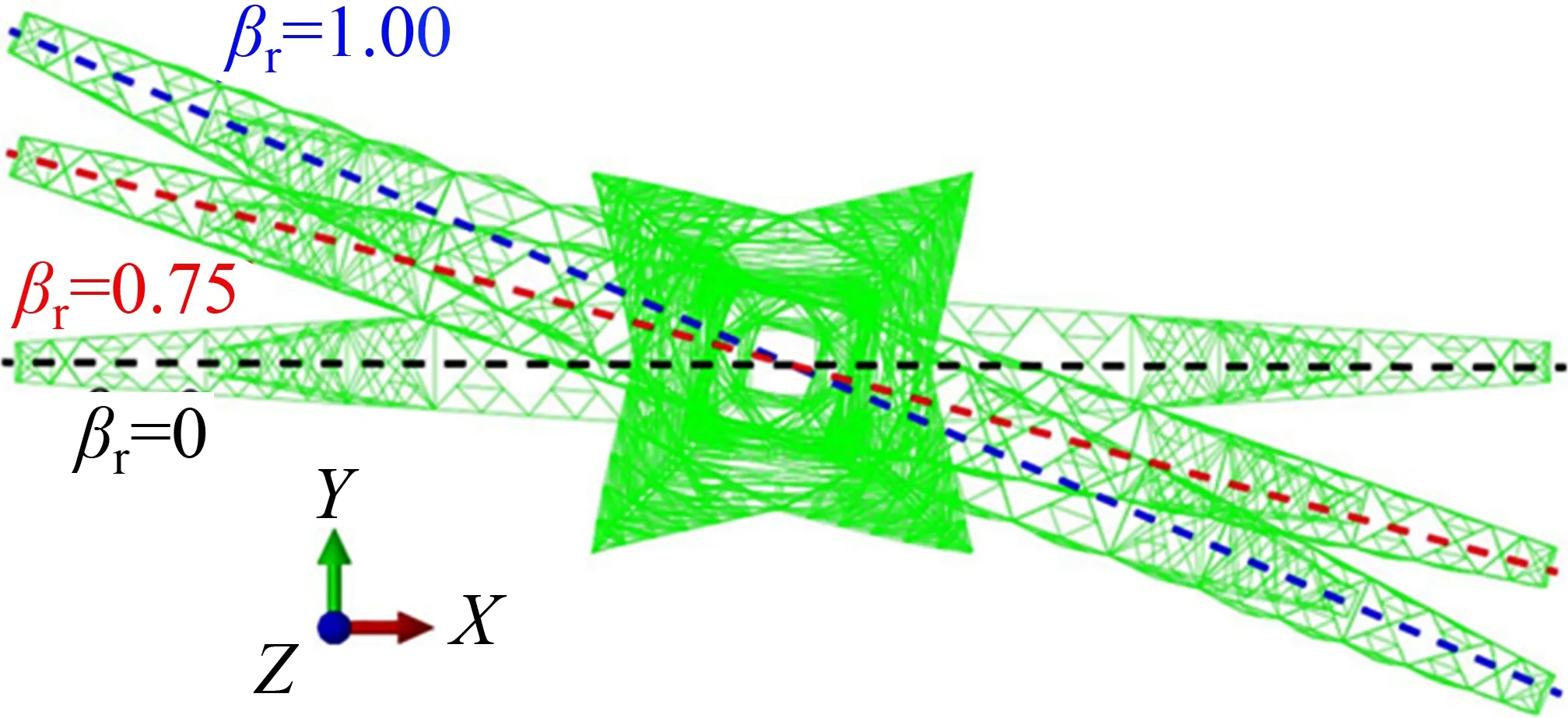
图8 不同等效扭转风振系数时的输电塔结构变形Fig.8 Deformation of transmission tower with different equivalent torsional wind vibration coefficients

2.3 风荷载响应计算结果对比

在横担中部、横担根部、塔身底部、塔身中部和塔身顶部5个部位的主材和斜材中分别选取代表性杆件，分析等效扭转风振系数对应的荷载工况对杆件内力的影响。以塔身底部斜材的一次时程分析为例，不同工况作用下的杆件应力计算结果如图9所示。由图9可见：不考虑等效扭转风振系数时，塔身底部斜材静力计算结果对时程分析得到的应力水平的包络程度较小，为75.34%，附加的扭转工况提高了斜材内力，增大对动力时程计算结果的包络程度，达到93.95%，多次时程计算结果如表2所示。

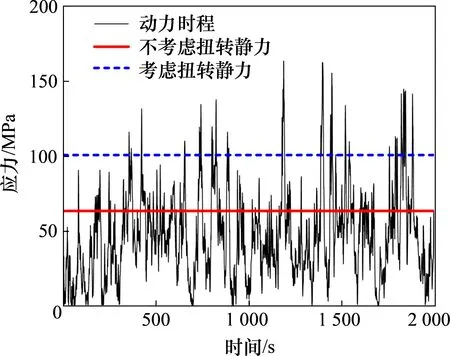
图9 塔身底部斜材应力计算结果对比Fig.9 Comparisons of stress calculation results of the oblique member in the bottom part of tower body

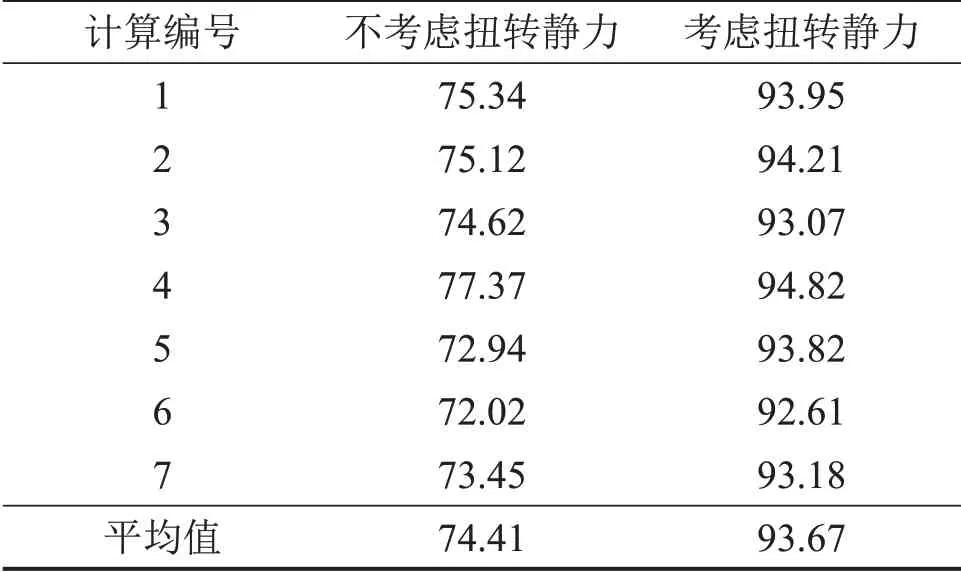
表2 底部斜材应力包络程度对比Table 2 Comparisons on stress envelop of the bottom oblique member %

对于输电塔主材和斜材的应力计算结果对比如图10所示。由图10可见：考虑扭转效应后，斜材杆件的应力提升较大，对动力时程分析结果的包络增大，而且塔身部分的斜材杆件比横担部分的斜材杆件的包络程度的增幅效应明显。对于主材，考虑扭转效应后横担部分杆件的包络程度增加效果比塔身部分杆件的大，但是整体上比斜材杆件的小。综上可知：考虑扭转效应可以增加杆件设计的可靠度，尤其是对塔身部分的斜材杆件设计可靠度提升效果明显，考虑扭转荷载的静力计算结果对动力时程计算结果的包络程度均在90%以上。

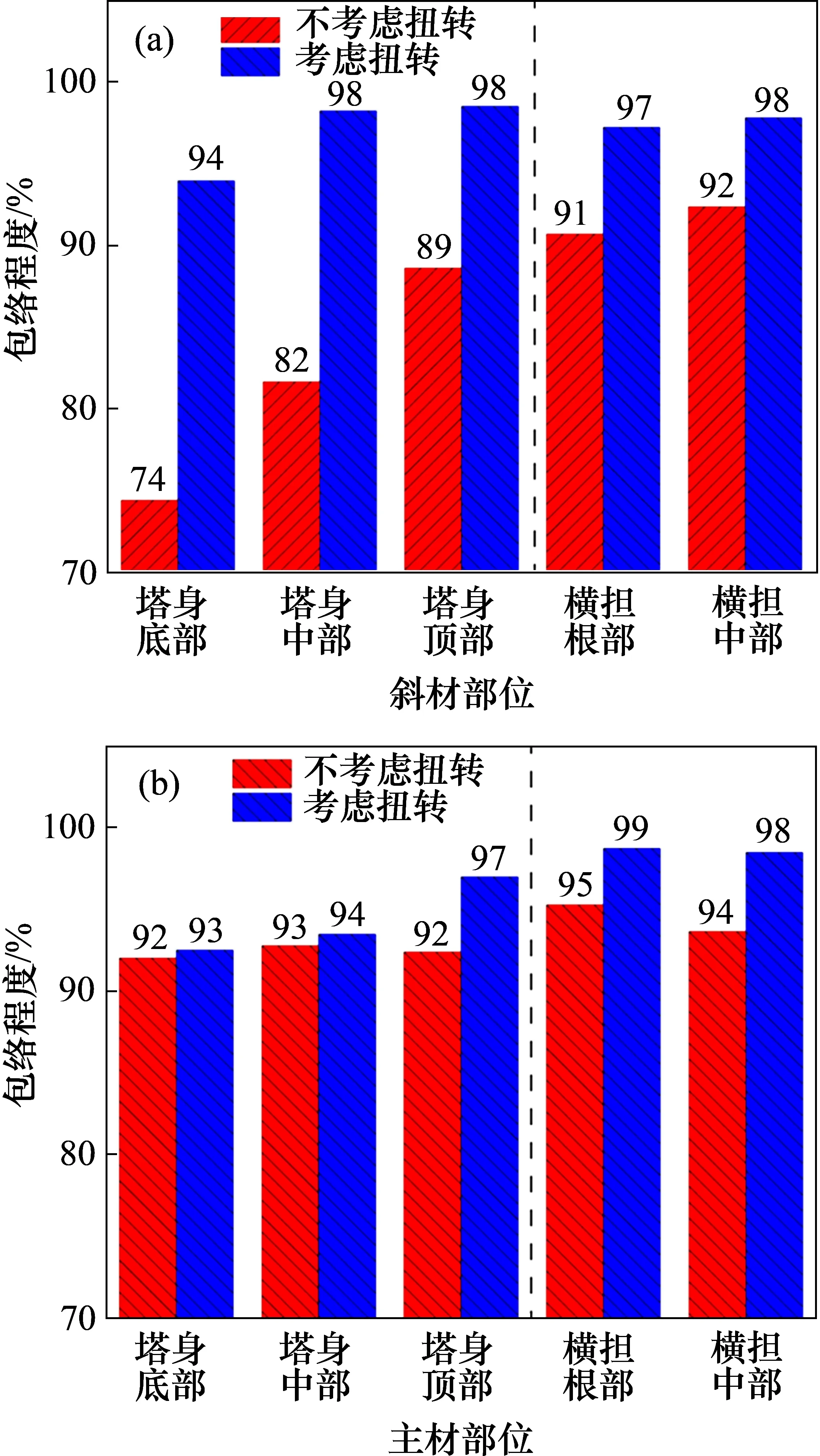
图10 输电塔杆件应力包络程度对比Fig.10 Comparisons on stress envelop of the transmission tower members

3 风向对扭转效应的影响

按照文献[21]，采用风向角分别为45°，60°和90°时的风荷载时程对输电塔结构进行动力计算，分析各种风向角时输电塔结构的扭转效应如表3所示。由表3可见：不同风向角时，长悬臂输电塔的扭转效应与垂直于横担方向(Y方向)的风荷载分配系数呈线性正相关，而与平行于横担方向的风荷载分配系数(X方向)无关，即横担的扭转效应只由垂直于横担方向的风荷载产生。

不同风向角时，等效扭转风振系数与扭转角呈线性正相关关系，45°和60°风的等效扭转风振系数分别为0°风的等效扭转风振系数的70%，90°风时，没有垂直于横担方向的风荷载分量，基本不产生扭转效应，可以认为等效扭转风振系数为0。

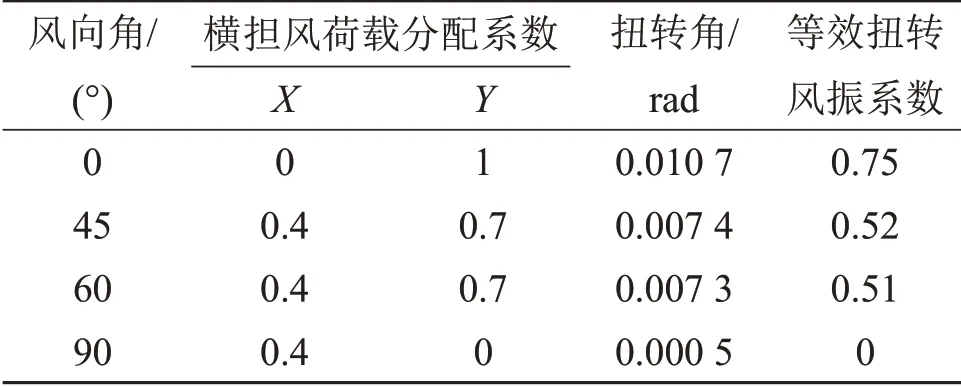
表3 不同风向角时输电塔结构的扭转效应Table 3 Torsional effect of the transmission tower under different wind direction angles

4 横担长度对扭转效应的影响

由第1节分析可知，横担总长度对长悬臂输电塔结构的扭转效应影响较大，本节不断改变长悬臂输电塔结构的横担总长度，计算输电塔结构在0°风作用下的扭转效应，其中，塔身信息不发生改变。表4所示为改变横担总长度后的输电塔结构的扭转阵型特征。由表4 可见：随着横担总长度减小，扭转频率逐渐增大，扭转振型的阶次逐渐提高，相应的频率扭平比逐渐降低。输电塔结构的扭转效应和等效扭转风振系数与横担总长度之间的关系如图11所示。

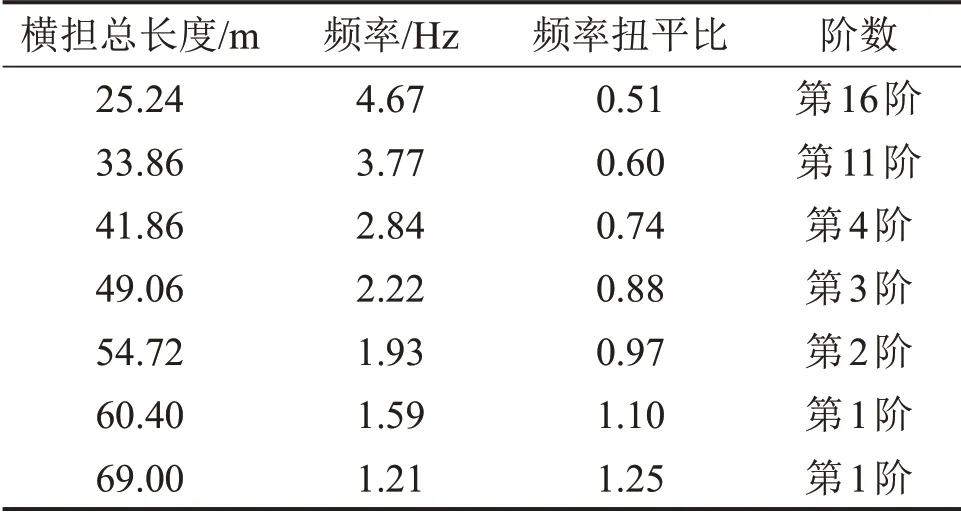
表4 不同横担总长度时的扭转振型特征Table 4 Torsional vibration mode characteristics with different lengths of the cross arm

图11 横担总长度对扭转角和等效扭转风振系数的影响Fig.11 Influence of total length of cross arms and torsional angle on the equivalent torsional wind vibration coefficient

由图11 可见：随着横担长度减小，横担部分的扭转角也逐渐减小，即横担扭转效应对输电塔结构的影响逐渐减小；且随着横担长度减小，等效扭转风振系数先逐渐减小，在横担总长度小于54.72 m 后稳定在0.55 附近，此时结构的扭转振型不再是一阶振型。因此，当输电塔结构的扭转振型为低阶振型时，会促进结构产生扭转效应。

5 结论

1)由于空间效应，作用于长悬臂输电塔结构的风荷载会在横担上产生非对称荷载，造成长悬臂输电塔结构的扭转。采用扭转角表征长悬臂输电塔结构扭转效应，并通过定义等效扭转风振系数描述附加的扭转荷载。

2)考虑扭转效应的静力风振分析可以提高塔身和横担的主材和斜材杆件的设计可靠度，其中对塔身部分斜材的可靠度提高最大。

3)不同风向角时的扭转效应和横担风荷载Y方向的分配系数呈正线性相关，和X方向的分配系数无关，横担的扭转完全由垂直于横担方向上的风荷载产生。

4)当长悬臂输电塔结构的横担总长度减小时，结构的扭转效应也逐渐减小，而等效扭转风振系数先减小后趋于平缓，拐点位置和结构的扭转振型对应的阶数相关。