冻胀过程管土相互作用规律及受力特征

2020-06-04黄龙盛煜吴吉春黄旭斌何彬彬张玺彦

中南大学学报（自然科学版） 2020年4期

黄龙，盛煜，吴吉春，黄旭斌，何彬彬，张玺彦

(1. 中国科学院西北生态环境资源研究院冻土工程国家重点实验室，甘肃兰州，730000；2. 中国科学院大学，北京，100049)

土体的冻胀会给油气管道工程带来安全隐患，引起管道变形甚至开裂，对诸多工程造成巨大威胁；如阿拉斯加管道、俄国远东地区管道、中国格尔木—拉萨原油管道等一些大型的长输管道，冻胀曾引起多次工程事故[1]，所以，针对冻土区管道及其它建筑结构(如房屋、桥梁、铁路、公路、隧道、管涵、洞室和通道等)的设计，冻胀的影响不容忽视。冻胀对管道的影响是一个相互作用的问题，管道受冻胀会产生附加应力和变形，而管道也会对周围土体的位移产生抵抗作用。掌握冻胀时管土相互作用的机理对管道的安全分析具有重要的意义[2]。20 世纪80 年代开始，NIXON 等[3-7]记录与监测埋地管道运行，并进行了简单的现场试验模拟，获得有效的工程应用模型；张海丰等[8]针对管土相互作用的土箱模型实验进行设计并阐述其原理，分析土压力分布、管道内应力特征及破坏机理；SHMULEVICH 等[9]采用箱形试验装置和平面应力传感器进行试验，获取管上应力分布。学者们针对管道的土拱效应[10]、地层沉陷作用[11]、管周土压力分布[12]、界面应力[13]、管周填土对管道静力及动力响应规律[14-15]等开展试验，考察多种因素对管土相互作用的影响。此外，CALVETTI等[16-25]在滑坡、地震、断层、隧道开挖和海底等不同环境条件下，研究了管道与土体相互作用(包括相对滑移、摩擦位移、沉陷和屈曲等)，但较少涉及冻土环境。目前为止，关于冻土环境下的埋地管道的试验研究手段及目标各不一样，或模拟管道的变形与运行，或测试管道的应力应变，或分析热输管道引起的多年冻土融化等，如1999—2003年，美国和日本的2所大学联合开展了大尺寸高寒地区埋地管道的模型实验，评估不连续冻土区管道的响应，并通过监测温度与位移得出管道周围冻土的热学效应以及融沉特性[26]。PARMUZIN 等[27]分析土壤的不均匀冻胀引起的埋地管道竖向位移及冻结管壁的附加应力，并通过室内试验和现场数据进行验证。21 世纪初，岩土离心模型试验机被用于研究地面变形和管道的冻胀融沉问题，该技术不仅模拟土壤和管道整体的运行模式，还考虑管内流体介质对管道的影响，评估管道受压情况[28]。刘啸奔等[29]对冻土区管道上浮屈曲进行模拟试验，研制了一套能模拟管道及输送介质自重、土壤力学特性、管道温升、管底冻胀及冻胀范围等参数的试验装置，可测试不同参数下管道屈曲时的变形和临界屈曲载荷。结合文献发现，针对冻胀条件下的管土相互作用的试验报道尚不多见，而且我国尚无比较完善的针对冻土区埋地管道的设计规范。在寒区埋地管线的设计中，通常以本区域土体的天然最大冻胀量为极限变形进行验算，但由于管道对冻胀的约束作用，实际中管底地基冻胀量远小于天然冻胀量。对于工程来说，极限变形的设计方法安全保守，但对管道材料性能的高要求导致工程造价高昂，势必会造成资源浪费。此外，管道与土体之间相互作用的原理目前多倚重于弹性地基梁模型，然而，将地基视作均匀的、各向同性的弹性体却满足不了冻土的复杂特性条件，且冻胀过程中管道与冻土之间的协调变化规律及受力特征尚无定性或定量描述，更无具体的室内试验进行过验证。为此，本文作者在室内开展冻胀条件下的管土相互作用机制试验，以期探索管道与土体在冻胀过程中的反应规律，以便为后期建立合理的冻胀条件下的管土模型以及冻土区管道设计应用提供参考。

1 试验概况

1.1 设备及材料

1.1.1 设备仪器

本试验所涉及的设备主要包括：MHU-1000CLUA小型环境模型试验机；敞口保温箱(长、宽、高和厚度分别为800，800，450 和50 mm)；管道及其支架；数据采集设备(包括CR3000、DT80、DT500 和DH3816 静态应变测试仪等)；计算机；各类传感器(包括温度传感器，量程为-30～30 ℃，分辨率为0.01 ℃；压力传感器，量程为5 MPa，分辨率为0.01 MPa；位移传感器，量程为50 mm，分辨率为0.01 mm；水分传感器，量程为0～100%，精度为±3%；耐低温电阻应变片，量程为0～20 000 μm/m，精度为1%～3%)。

1.1.2 管道

为选取最符合本次试验的管道，对各类不同材料(如钢管、铜管、PVC管等)和尺寸的管道进行一系列材料及力学性能试验，根据各类管道的承载能力和变形情况，结合前人经验，最终采用201不锈钢管作为本次冻胀试验用管道。管道具体参数为如下：计算长度为660 mm，外径为38 mm，壁厚为0.8 mm；弹性模量为203 GPa，抗拉强度为520 MPa，屈服强度为275 MPa。

1.1.3 土样

本次试验用扰动土均取自黑龙江省黑河市。根据土样界限含水率试验结果(初始含水率w0为4.63 %，液限wL为35.1 %，塑限wP为22.8 %，塑性指数Ip为12.3)及颗粒级配[30]，重塑土样可定性为冻胀敏感性粉质黏土。试验土样含水率为10 mm液限含水率，设计含水率为35.1%，初始干密度为1.49 g/cm3，试验用土质量为170.19 kg，用水质量为59.74 kg，配制的土样总质量为229.93 kg，土样参数计算中需减去埋在土中的管及管支架的体积。箱内填装土和砂总厚度为350 mm，其中土层厚度为250 mm，箱底垫砂层为100 mm。

1.2 试验方案

本试验在小型环境模型试验机中进行，可准确地控制箱内温度。土体与管道支架(包括管道)填埋于敞口保温箱内，同时箱壁周围采用保温棉包裹。在整个试验过程中，开启所有的数据采集仪器实时监测土体及管道，数据采集间隔为5 min。试验结构示意如图1所示。

试验的主要步骤包括基础试验、支架安装、土样配制、样品填装及设备安装、控温过程和含水率测试等，具体流程如图2所示。封闭后静置的目的是让土样充分混合沉淀均匀。从下往上逐次填土并同步布置各类传感器。在填装过程中，砂、土分层捣实捣密，排出土样中的气泡，同时需注意防止损坏传感器。含水率测试完毕后，将试验箱打开，整个土样将在自然室温条件下逐渐解冻。

1.3 试验测点布置

试验中所有测点的布置如图3所示。其中L为沿着管轴线的方向，W为垂直管轴线且水平向前延伸的方向，H为垂直管轴线竖直向下的方向。试验测点分电阻应变片、传感器以及含水率3 部分布置。

1.3.1 电阻应变片

试验开始前，先将耐低温应变片黏贴在管道相应位置(如图3(a)所示)，并做好防水处理；沿着管道轴向分为4 个截面，依次为1/8，2/8，3/8 和4/8 截面，每个截面布置3 个测点，分别在管顶、管侧和管底处，每个测点分别沿着轴向和环向黏贴2 片，总计24 片。接着将管道按照试验设计的约束类型固定在支架上，并将管道及支架整体摆放到试验箱的中间位置。

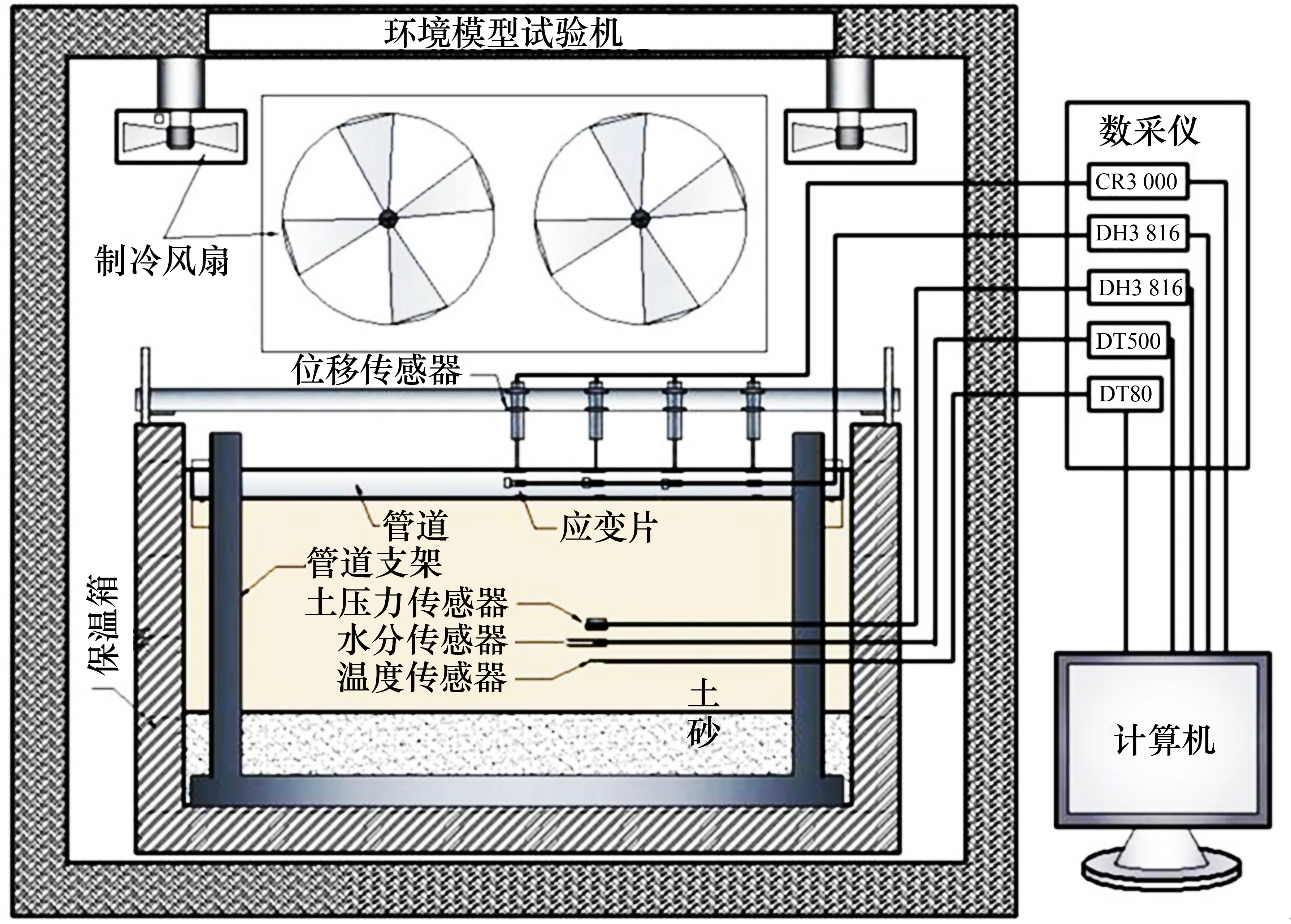
图1 试验设备示意图Fig.1 Schematic diagram of experimental setup

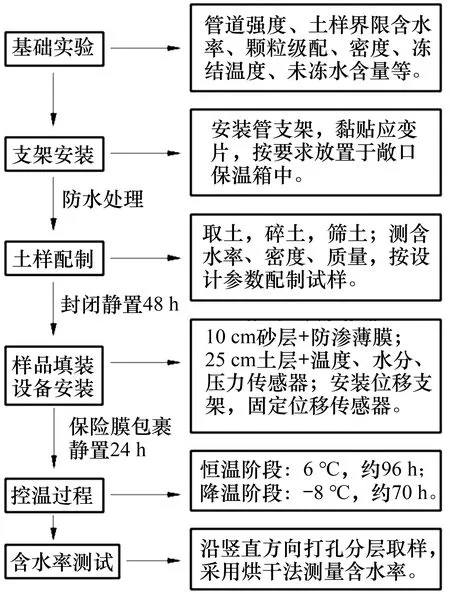
图2 试验流程Fig.2 Experiment flowsheet

1.3.2 传感器

试验涉及各类传感器总计89 个，布置方案如图3(b)所示，具体设置过程如下。

1)在填土过程中，温度、水分及土压力传感器自下而上布置4层，每层分别距离上表面深度H为50，125，200和275 mm；每层按照管底轴向1/8，2/8，3/8 和4/8 这4 个截面分为4 组，共计16个。

2)在每层的4/8 截面且距离管轴线100 mm 及250 mm 的管侧分别布置2 组温度、水分及土压力传感器，共计8个。

3) 在土体上表面(H=0 mm)额外放置1 个温度传感器用来监测土表温度。

4) 位移传感器沿着上表面1/8～4/8 截面布置4组，每组按距离管轴线0，50，150和250 mm安装4个，共计16个。

另外，土体内部布置的传感器虽多，但考虑到它们的体积均较小，故忽略其对土体冻胀性质的影响。

1.3.3 含水率测点

按照管轴向1/8及4/8这2个截面布置2组，每组在距离管轴线20，150 和300 mm 处分别布置3个测点，共计6个，如图3(b)所示。

2 试验结果

2.1 土体的冻结

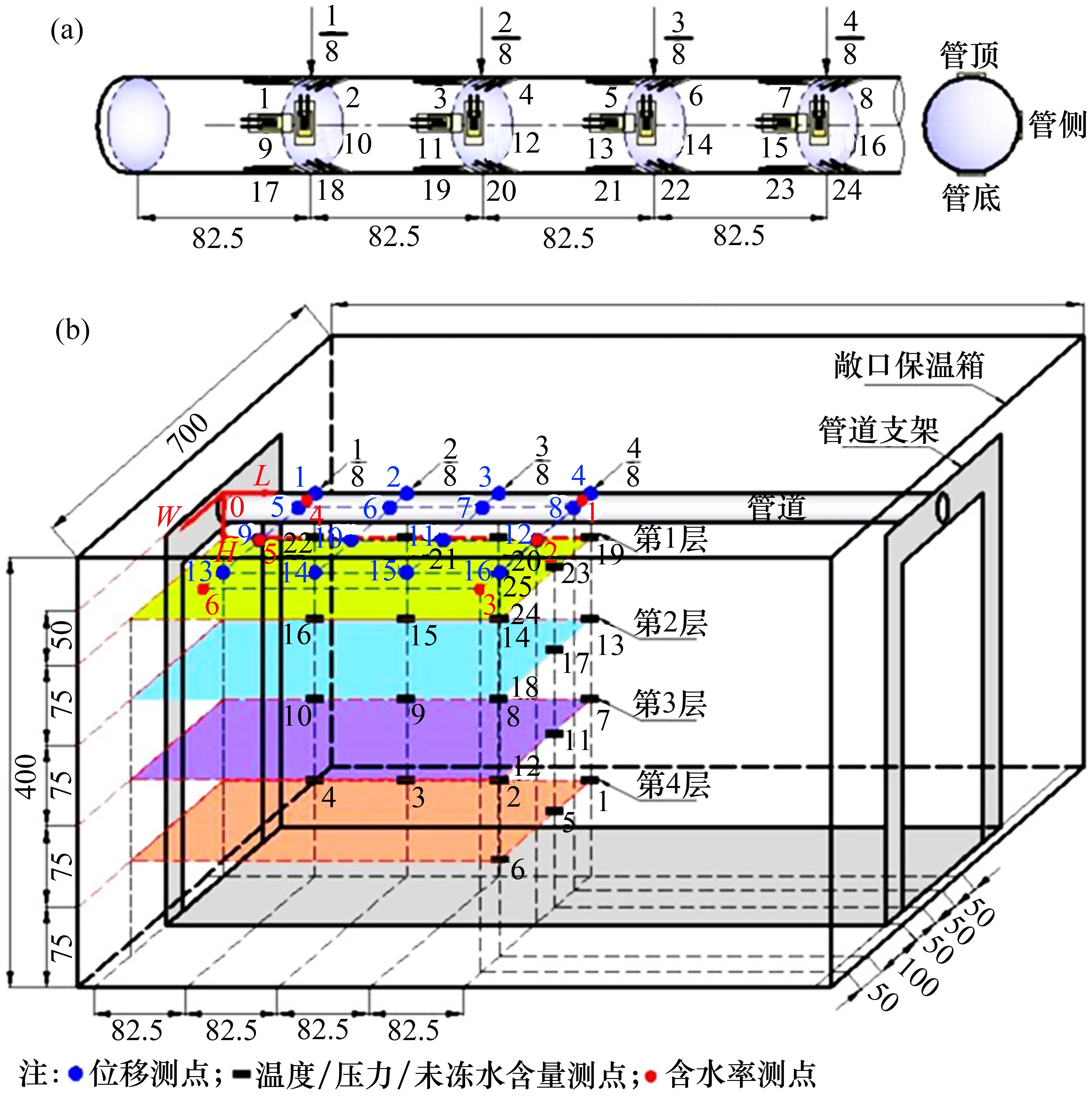
图3 测点布置Fig.3 Arrangement of measuring points

本试验结果主要分析降温阶段即土体的冻胀过程，且在试验过程中没有外界水源补充。在土体冻结过程中，标志冻结特性的变量包括温度梯度、冻结深度、冻结速率和冻结锋面等，而温度是发生冻胀的先决环境条件。试验结果以总的温度控制流程和温度传感器布置点所测数据为依据，根据土体温度随深度分布得到冻结锋面(冻土与未冻土之间的接触界面)，本节采用-0.18 ℃冻结温度移动的位置(冻结深度Hf)来判断。与此同时，观测到4个典型时间点，即t0=0 h，降温开始；t1=25 h，冻结锋面到达50 mm深度；t2=45 h，冻结锋面到达125 mm 深度；t3=70 h，降温结束，冻结锋面到达200 mm 深度。图4 所示为不同时刻土体温度随深度的分布。

以t0～t3时刻为例进行分析，获取不同时刻管底土体剖面的温度变化如图5所示。由图5可见：降温前土体整体恒温在6 ℃左右；在降温过程中，温度从土体表面自上而下随着时间逐渐降低；试验持续到70 h 时停止，此时，200 mm 深度处的土体温度降低到负值，且上表面最低温度达到-8 ℃。-0.18 ℃温度线移动速度也间接反映土体的冻结速度，图5中对应的同一深度处不同的测点到达负温的时间分布略有差异，这是由于箱侧保温不理想导致四周的土体温度比中间的温度降低略快，但误差较小，可以忽略其对试验的影响。

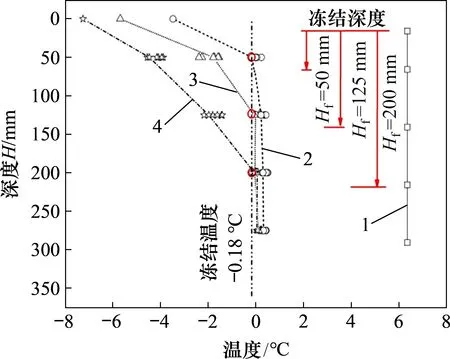
图4 不同时刻土体温度随深度分布Fig.4 Distribution of temperature with depth at different time

2.2 土体含水率

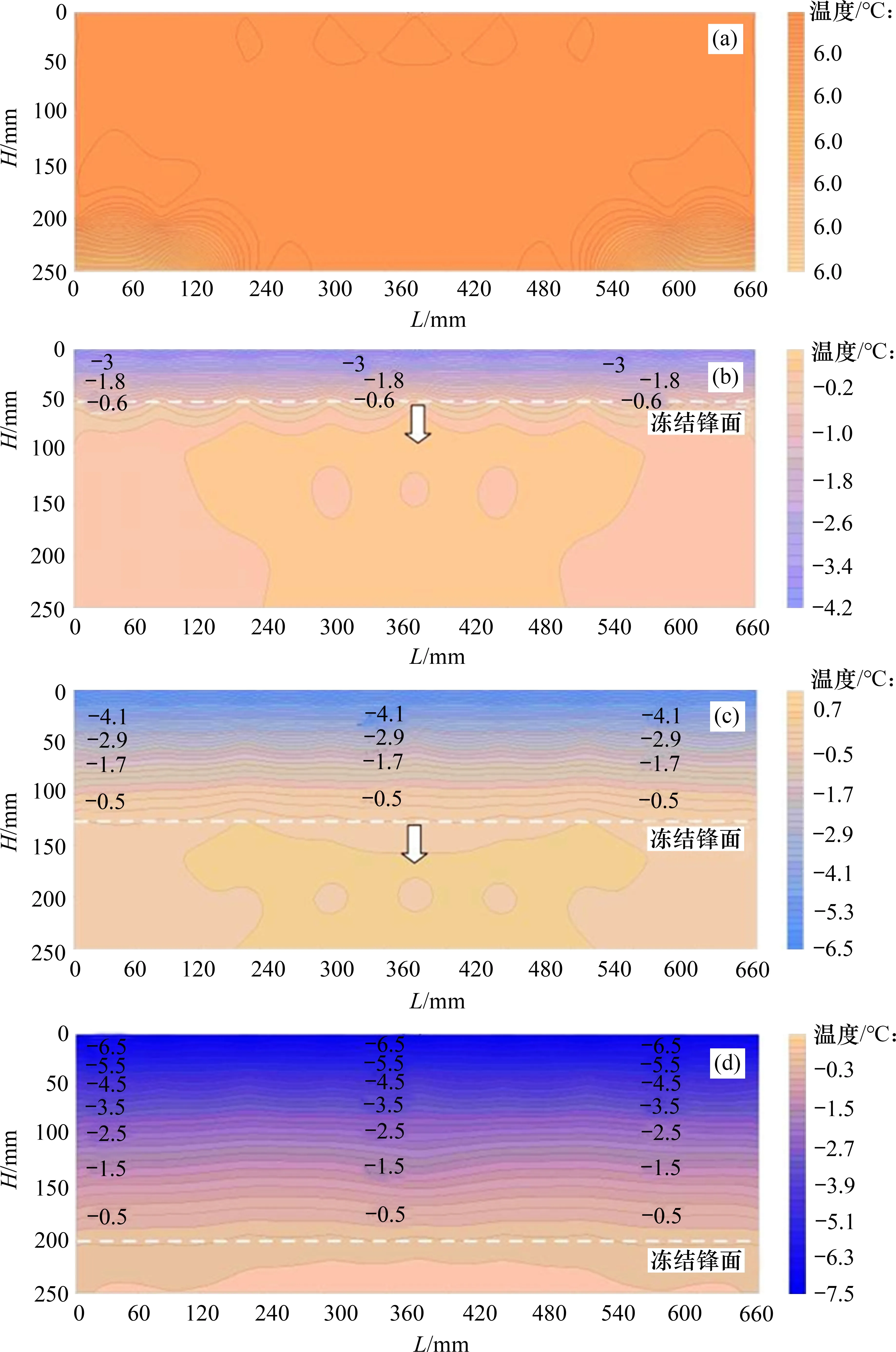
图5 降温过程中管底土体剖面的温度变化Fig.5 Temperature variation of soil profile below pipe by cooling

试验采用的水分传感器所测得未冻水体积分数φu反映传感器周围小范围地区液态含水率的变化。降温过程(t0→t3时刻)未冻水体积分数分布如图6 所示。由图6 可见：土体自上而下发生冻结，未冻水含量与温度保持着动态平衡；土体上表面冻结时，上层土体内部的未冻水含量下降，随着温度降低，未冻水含量不断降低，由初始最大值40.44%下降至最小值15.63%。已冻区未冻水含量发生大幅度降低的同时未冻区的含水量也降低，因而，上层未冻水含量高的区域界线向下移动，且在冻结锋面附近未冻水含量变化最不明显。

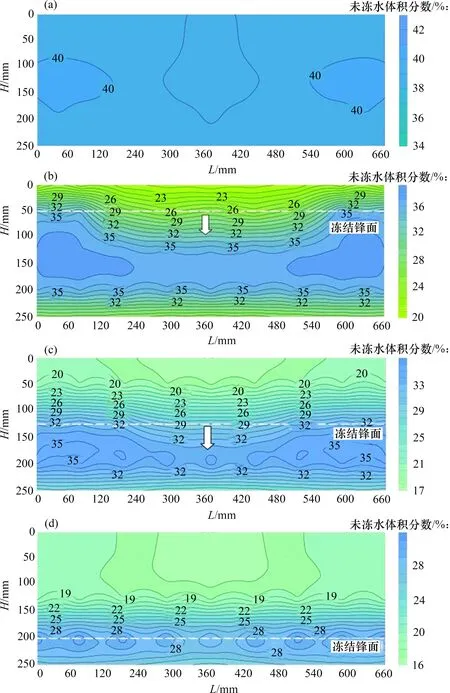
图6 降温过程中未冻水体积分数变化Fig.6 Variation of unfrozen water volume fraction below the pipe by cooling

为更进一步证明冻胀过程发生水分重新分布，观察试验结束(t3)时1/8 截面和4/8 截面测点的含水率wm(打孔取样并烘干测量)，如图7 所示，从图7可见：在200 mm 深度处，土体含水率均大于35.1%，意味着该部位已发生冻结；试验结束时，冻结深度恰也到达200 mm深度位置，此处也是冻结锋面在t3时刻所在的位置。冻胀结束时的冻结锋面也可由断面含水率存在明显突变的位置判断。土样在200 mm 深度之上含水率变大，即为冻土区；在200 mm 深度之下含水率变小，即为未冻区；在200 mm深度位置存在峰值，即为冻结锋面位置，与前面冻结温度判断的结果相吻合；且4/8截面冻土区的含水率较1/8截面的含水率大，表明管道对不同截面影响不同。以上现象表明土体在冻结过程中发生水分迁移，而且在温度相同的条件下，管道对管底土体的约束是影响冻结过程中含水率变化的重要因素，而对于约束、水分迁移及冻胀量等之间的关系需进一步通过机理试验并结合管土作用过程力与变形的规律进行验证。

2.3 管道和土体的冻胀变形

降温开始后，实时监测土样上表面冻胀以及管道变形。当土体表面发生隆起现象时，土体已开始冻胀；随着时间推移，冻胀逐渐增大；当冻结深度达到200 mm 时(即t3时刻)，冻胀达到最大值。假设管道两端发生对称变形且管道两侧土体的冻胀呈对称增大，根据监测结果，取t0～t3时刻上表面位移测点进行分析，以降温前的上表面为初始平面，并在此基础上计算得冻胀过程中不同时刻的管道变形量Δ及土体表面冻胀量δ随时间增长如图8和图9所示。

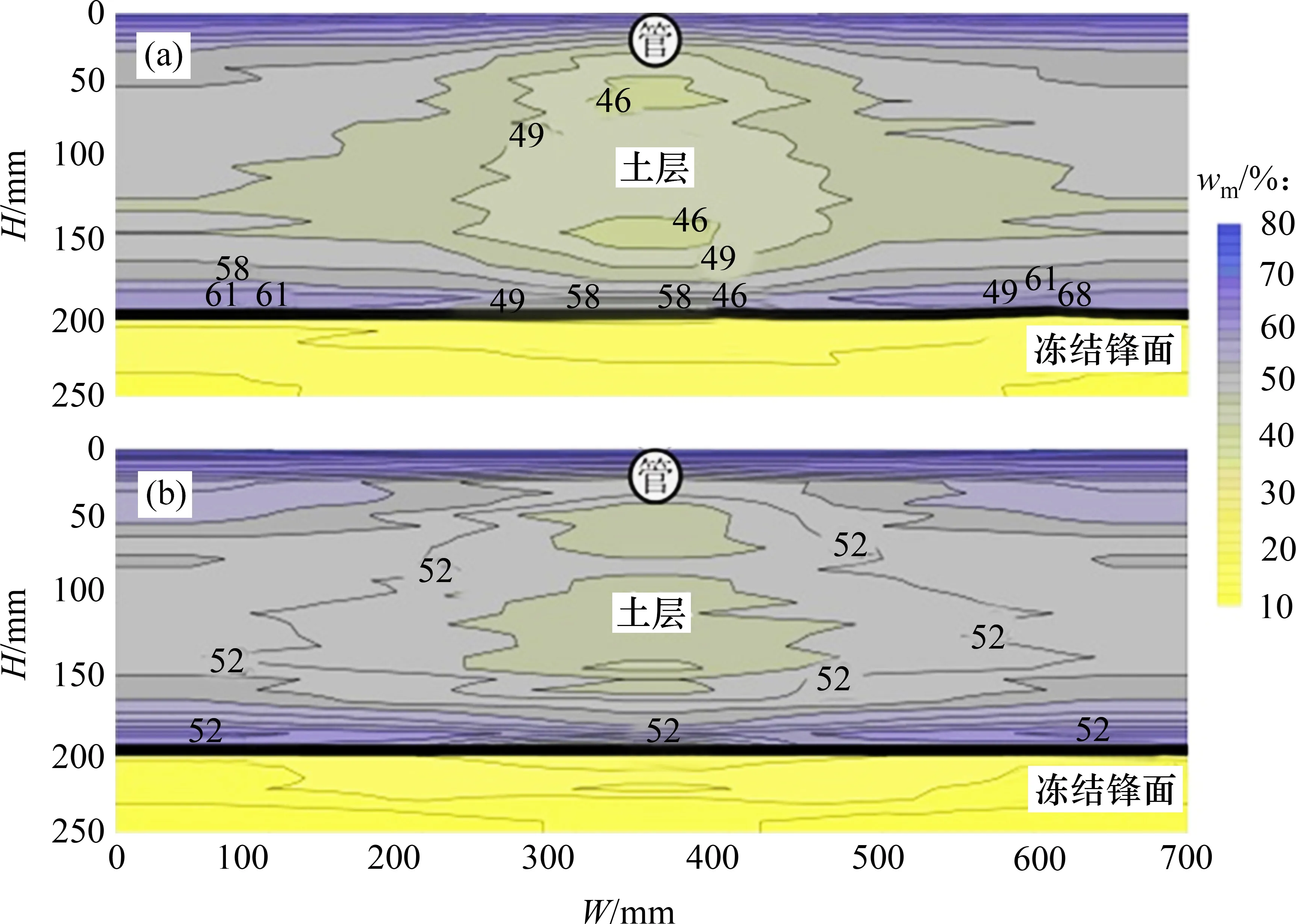
图7 试验结束后不同剖面含水率分布Fig.7 Distribution of water content in different profiles after test

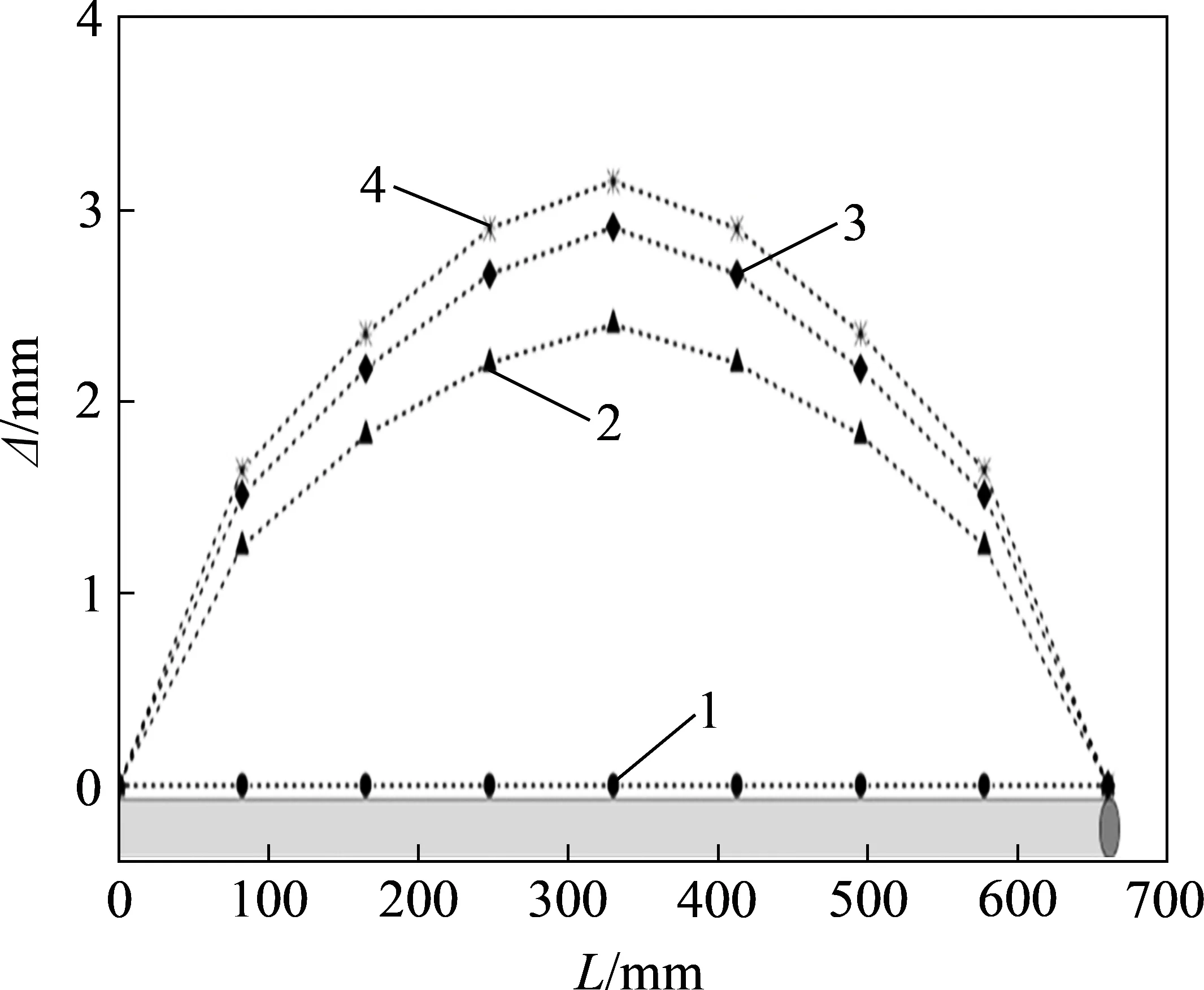
图8 不同时刻管道竖向变形Fig.8 Vertical deformation of pipe at different time

由图8 可见：冻胀发生后，管道发生翘曲变形，并随着管底及管侧土体的冻胀而持续增大。距离管端越近，管道变形越小，且在中间位置呈现最大值；管中最大变形在t0～t3时刻由1.09 mm增大至3.16 mm，而整个上表面也因冻胀而逐渐变形为高于初始平面的曲面，如图9所示。假定管道与土体在冻胀过程中紧密接触，管底土体的冻胀也呈现出和管道类似的变形，即管底土体的冻胀量在靠近管端的地方较小，而在管道中间位置也呈现最大值。在同一时刻管轴线两侧土体的冻胀明显大于管底土体，管中4/8 截面距离管轴线50，150和250 mm断面最大冻胀量分别达到6.11，7.04和7.21 mm，表明距离管轴线越远的位置冻胀量越大。

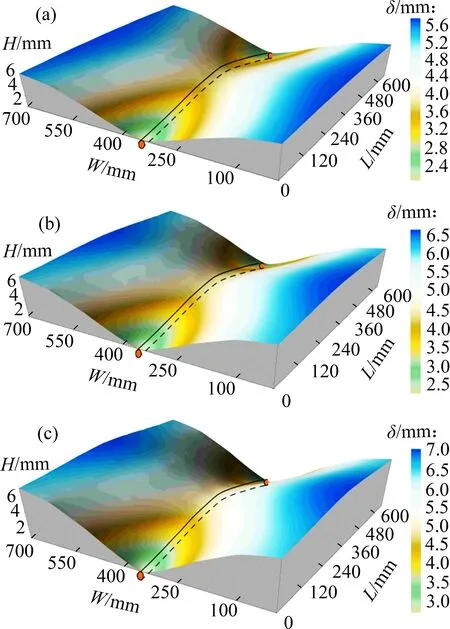
图9 不同时刻土体的冻胀量Fig.9 Frost heave of soil at different time

2.4 土压力分布

土体冻胀过程中因受到管道的约束而产生冻胀力，而管道也对管底土体存在抵抗作用，导致试验箱中冻胀部分对未冻土产生挤压，挤压程度可通过土压力传感器间接测量，所测土压力也可间接反映冻胀力的变化趋势。此外，使用的传统土压力传感器存在失效的问题，即在冻结锋面到达传感器所在位置后，传感器周围土体发生完全冻结，并在冻结土体的包裹下与其自身融为一体导致传感器感应失效，失效时刻具体为：50，125和200 mm 深度处冻结锋面到达时间分别为25 h(t1)，45 h(t2)和70 h(t3)。此外，为了观察压力分布规律，在以上特殊时刻的基础上，再添加4个时间点，即5，15，35 和55 h。剔除失效之后的压力，在土压力传感器的有效时刻内，分别取不同深度不同时刻的土压力在管底及管侧的分布，如图10和图11 所示；25 h 时不同深度的土压力沿管线分布如图12所示。

由图10 可知：土体内部同一位置处的土压力随着冻胀增大而持续增大，即随着冻结加深，上部冻土体受管道约束后对下部未冻土层产生的挤压越来越强烈。对于管底的土压力，在同一深度同一时刻的不同测点处，越靠近管端的位置，土压力越大，反之越小(如在t=25 h，50 mm深度处，1/8 和4/8 截面测点的土压力分别为24.82 kPa 和10.5 kPa)。而同一时刻沿着管底相同测点的垂直方向，土压力总体逐渐减小(图12)，原因在于土压力沿垂直方向存在着扩散现象(如t1=25 h，3/8 截面，H=50，125 和200 mm 深度处的土压力分别为14.28，8.65和7.62 kPa)。

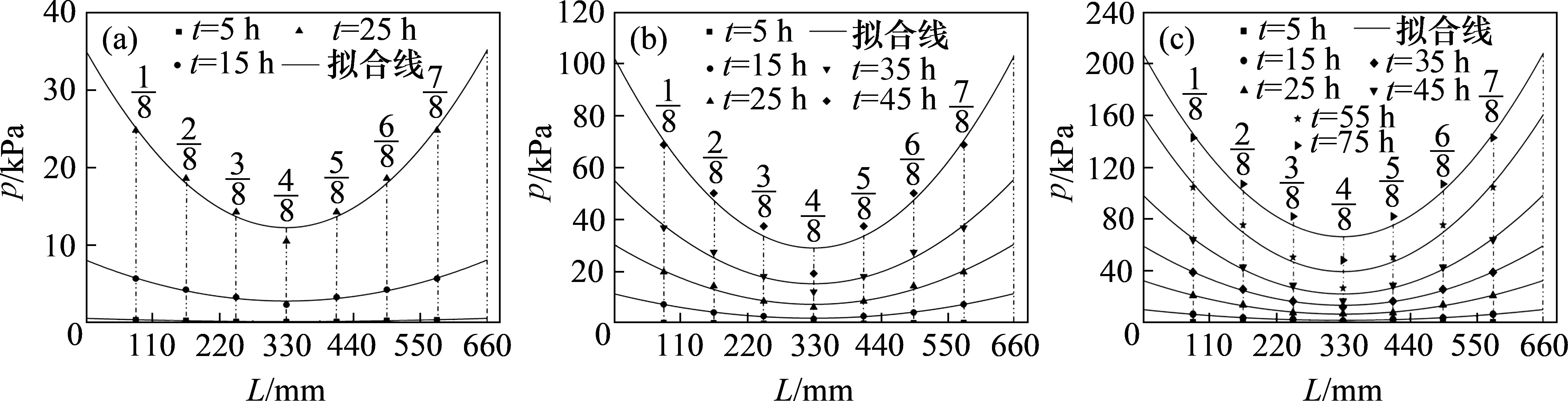
图10 不同深度不同时刻的管底土压力分布Fig.10 Distribution of soil pressure below pipe at different depths and time

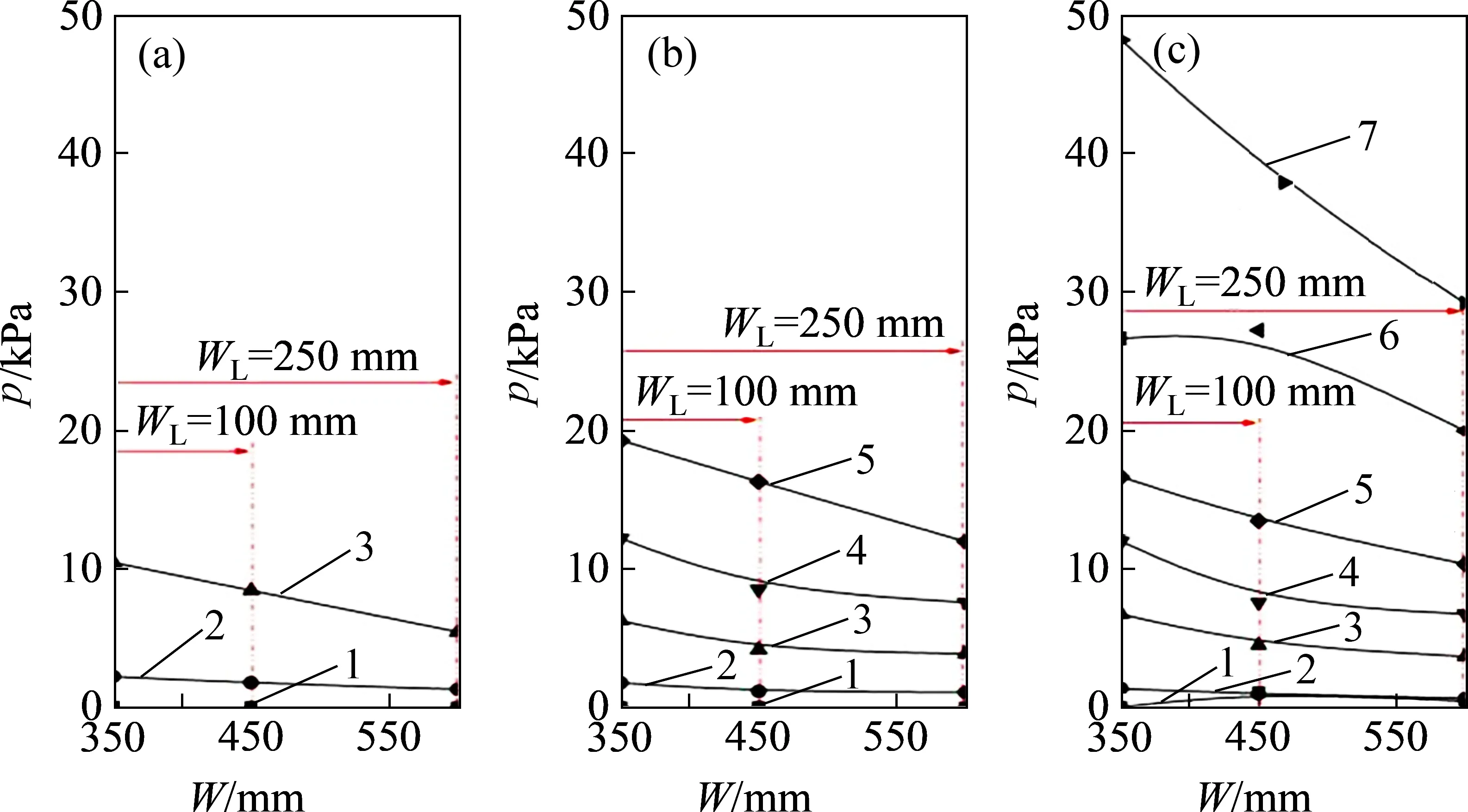
图11 4/8截面不同深度不同时刻的管侧土压力分布Fig.11 Distribution of soil pressure in 4/8 section on side of pipe at different depths and time

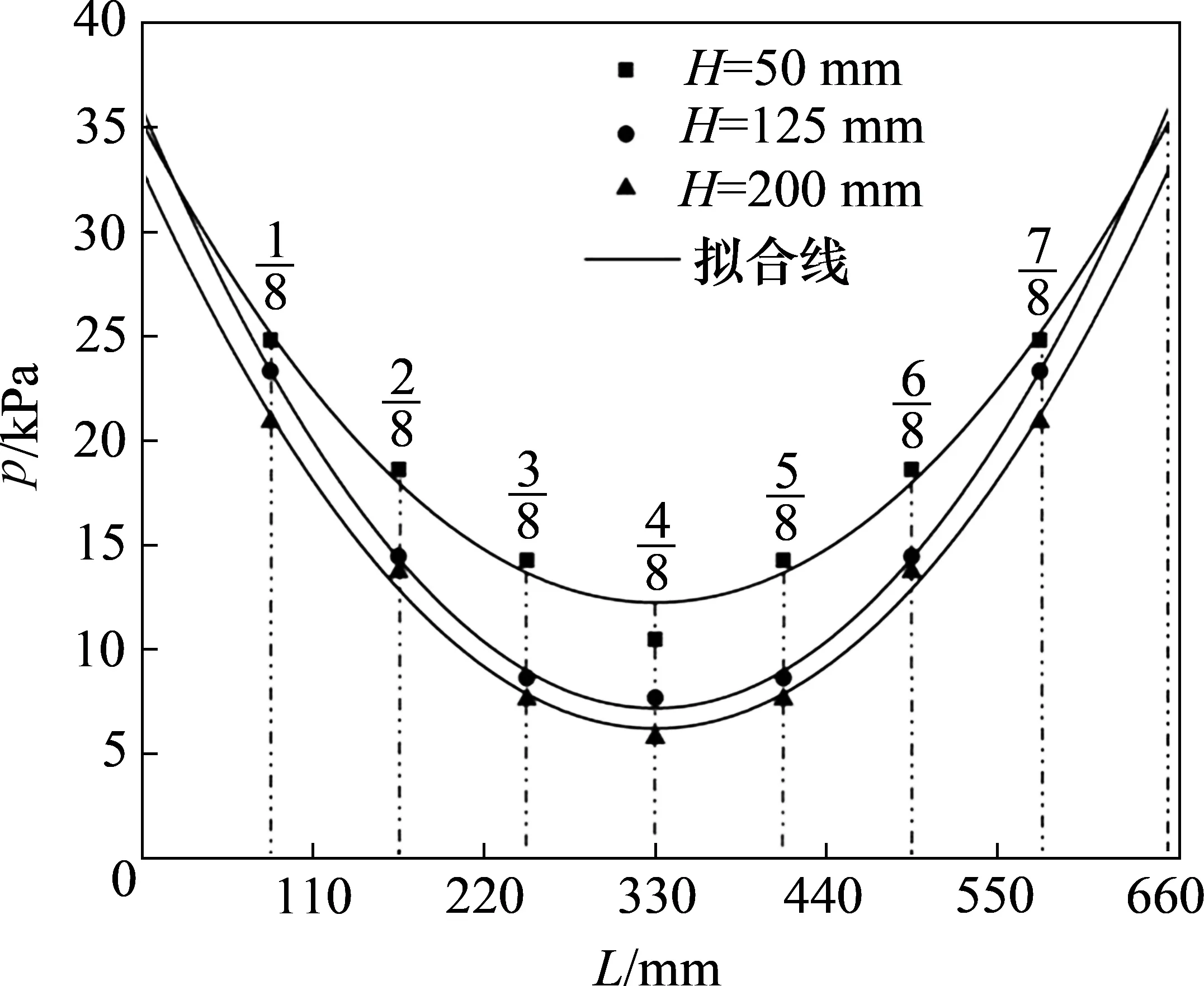
图12 25 h不同深度管底土压力分布Fig.12 Distribution of soil pressure below pipe at different depths at 25 h

由图11 可见：对于管侧的土压力，同一时刻同一深度处管侧的土压力均较管底的小，且距离管轴线越远的位置，土压力越小(如4/8 截面，t=45 h，125 mm深度处，在管轴线距离WL为0，100和250 mm 测点的土压力分别为16.30，16.32 和12.01 kPa)。结合2.3节中管道和土体的冻胀变形规律，不同位置的土压力分布规律恰也印证了管道对土体冻胀的约束程度，即约束越强的位置管底土压力越大；管侧土体虽没有受管道的直接作用，但土体的冻胀依然受管道约束影响，距离管轴线越近的位置，受管道的影响越大，因此，管侧土压力呈现由近及远而变小的规律。

2.5 管道应力

管道与土体之间因冻胀而发生相互作用，这种作用力反映在土体上表现为土体内部压力的变化，反映在管道上则表现为管道应力的变化。对于管道而言，对土体约束的强弱也反映着管道竖向变形，两者之间存在一定的关系。管道发生翘曲变形后，即表明管道发生轴向甚至环向拉压应变。

为了解管道的应力分布，借助于管道表面黏贴的耐低温应变片所测得的应变来计算应力。根据应变片的原理，当黏贴部位沿着黏贴方向受到拉伸时应变呈正值，而受到压缩时应变值呈负值，故换算后的管道应力在不同的位置呈现不同的正负数值。试验中通过应变片所获取的应力是所贴位置处测量区域内的平均应力，它只能表示截面该区域受力，但不能说明分布应力在截面该点的强弱程度[31]。另外，由于钢材会在低温下发生自身的冷缩现象，抵消一部分因冻胀引起的管道轴向和环向应变，因此，采用相同规格的管道进行一组温度效应试验，分别在管1/8～4/8 截面黏贴应变片，试验最终得到温度与应变的关系如图13所示。

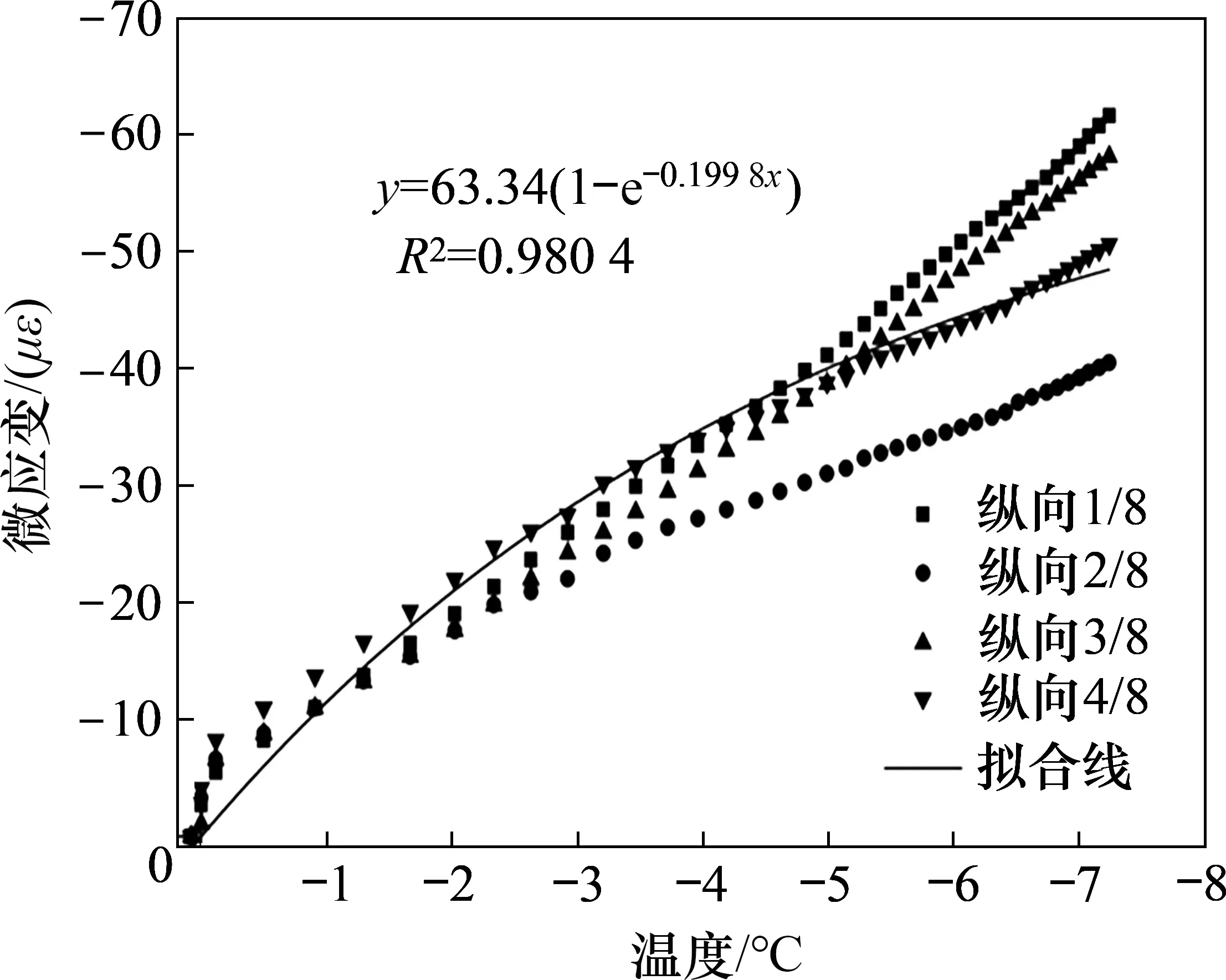
图13 降温引起的管材应变Fig.13 Strain of piping material caused by cooling

冻胀试验结束后，在进行管道应力和应变的分析时，假设管道弯曲变形只发生在轴向对称面内，无侧向弯曲，故实测应变需考虑温度引起的管材应变后才接近真实的应变。假设材料在拉伸和压缩时的弹性模量相等，且均在弹性范围之内，换算得管道各处轴向应力(σa)及环向应力(σc)，如图14所示。

由图14 可知：随着时间发展，管顶轴向应力呈正值且逐渐增大，管底轴向应力呈负值降低，而管侧轴向应力也有小幅度升高，但数值相对较小；这表明管顶受到轴向拉伸，同时管底受到轴向压缩，如果忽略管侧轴向变形，以上应力规律证明在冻胀力的作用下管道发生了向上的弯曲变形。此外，管顶、管底环向应力随时间呈负值降低，即管顶、管底受到环向压缩，同时管侧环向应力呈正值增大，即管侧受到环向拉升，表明管道同时也发生截面变形。取t3时刻即冻胀结束时的4/8 截面测点(最不利测点)应力进行比较，其中，管顶存在最大轴向应力和最小环向应力，分别为221.54 MPa 和-49.15 MPa；管底存在最小轴向应力和最小环向应力，分别为-195.53 MPa 和-61.51 MPa；管侧则存在最大环向应力为213.01 MPa。所以，就数值而言，管中的应力绝对值最大，越靠近管端各应力绝对值越小。

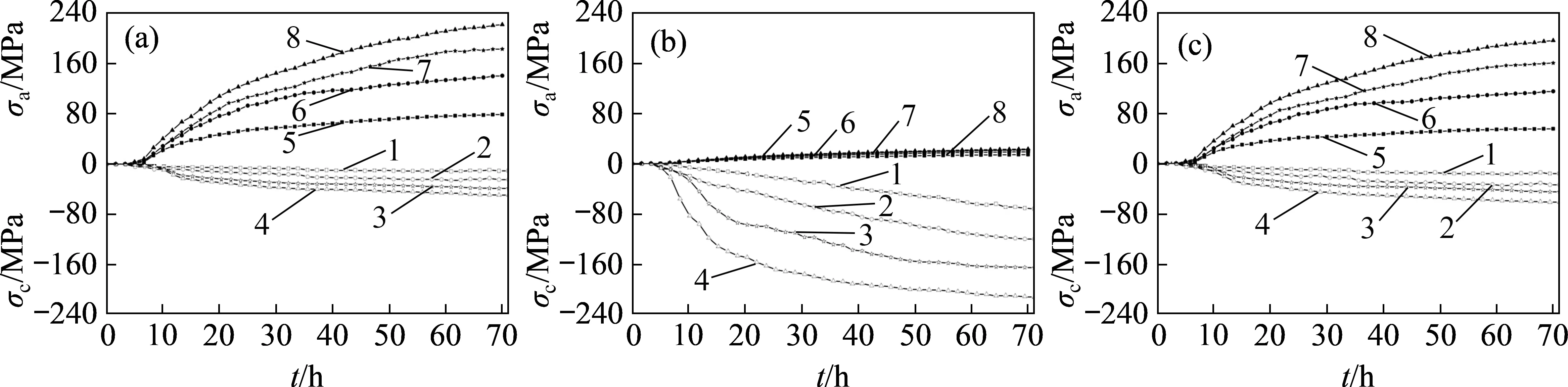
图14 管道轴向及环向应力随时间变化Fig.14 Changes of axial and circumferential stress with time

3 讨论

本试验作为室内机制性试验，在试验模型的设计中并不完全满足相似准则。选择简支仅是为了考虑试验的易操作性，但并不影响试验中对管道与土体相互作用规律的探讨结果。

3.1 土体冻胀对管道的影响

冻胀引起管道翘曲变形的过程也是管道产生应力应变的过程，而管道的应力分布规律也证明管道发生了向上的弯曲变形，在最不利的管中位置应力呈现最大值。假设管道与土体紧密接触，则管底土体的冻胀与管道的竖向挠度相等。由于受到环向应变以及其他外在因素的影响，管顶与管底的轴向应力绝对值不相等，但数值相差很小，所以，以管顶的应力代表整个管道的轴向应力变化趋势。

图15 所示为轴向应力σa沿轴向分布及环向应力σc沿环向的分布情况；由图15(a)可见：在管底冻胀量越大的位置，管道竖向变形越大，弯曲变形引起的轴向应力也越大。此外，假设管道截面变形对称，以1/4 圆周为例分析管道4/8 截面的环向应力分布(如图15(b)所示)，当管道遭受冻胀力较大时可能发生截面形变，应当在管道的稳定性分析中予以考虑。在实际管道工程中，冻胀可能会导致管道翘曲变形而外露地表，严重者是当冻胀引起的管道应力超过材料极限值后，管道发生截面破坏。

3.2 管道对冻胀的约束作用

受管道约束作用影响最直接的外观表现是不同位置处冻胀的差异，而约束影响冻胀的内在机理则表现为对水分迁移的抑制作用。在冻胀过程中，冻胀力与管道约束力为1 对作用力与反作用力，其值虽不等同于土压力值，但变化趋势与土压力保持一致，故土压力随着冻胀量增大呈现指数递减的规律也间接体现冻胀力与冻胀量的变化关系，且冻胀时间越长，这种关系表现越显著，如图16所示。

为了表现管道对周围土体的约束程度，定义变量约束率θ，其物理意义为与无约束的自由冻胀相比较，因约束而导致减少的冻胀变形所占的比例，计算公式为

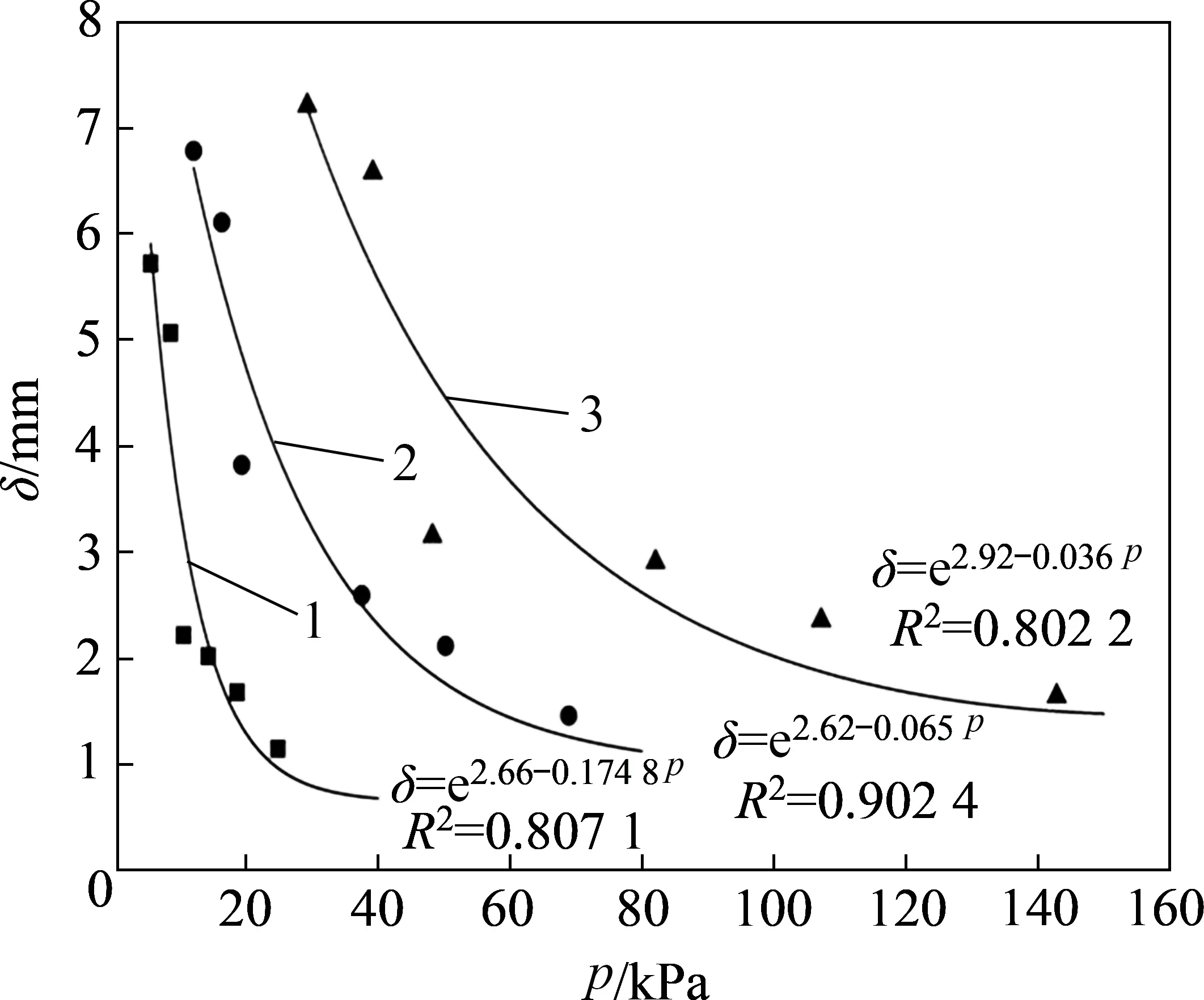
图16 土压力与冻胀的关系Fig.16 Relationships between soil pressure and frost heave

式中：θ为约束率，%；δm为无荷载无约束条件下的最大自由冻胀量，mm；δ为某位置受管道约束作用下的冻胀量，mm。以4/8 截面距离管轴线超过250 mm以外区域(管道几乎对冻胀没有影响的位置)视为自由冻胀区，则该区自由冻胀量为整个试验土体的最大冻胀量。管道的约束作用造成各变量之间不同程度的关联，导致土体内未冻水向冻结锋面的迁移量减少，最终影响冻胀增大。

由于冻胀量的获取是以土体上表面的位移测量而得，是总的冻胀变形，而内部土层的冻胀无法得知；试验土柱的含水率也是降温结束时刻(t3)所测，所以，含水率与其他变量之间的关系也以t3时刻的数值来分析；对冻土区含水率wm沿垂直方向求平均值，得到6 个测点处的平均含水率wam，它体现冻胀结束后水分迁移量；土压力p取第3层(H=200 mm)的土压力；并以t3时刻的冻胀量计算得不同位置的约束率如图17 所示。显然，约束率由1/8截面向4/8截面逐渐降低，且距离管道越远，约束率越小。

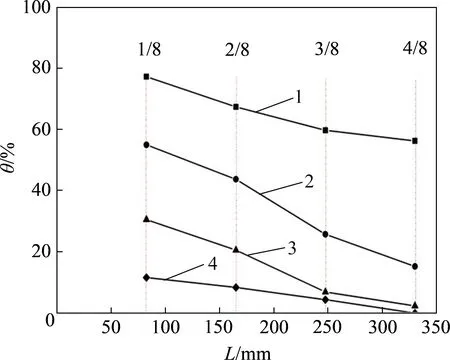
图17 不同位置处的约束率Fig.17 Constraining rate at different positions

结合图8 和图9 可知：由于管端受支座限制，越靠近管端，管道竖向变形越小(Δ(1/8)＜Δ(2/8)＜Δ(3/8)＜Δ(4/8))，意味着管道对管底土体的冻胀约束越大(θ(1/8)＞θ(2/8)＞θ(3/8)＞θ(4/8))，管底土体的冻胀量则越小(δ(1/8)＜δ(2/8)＜δ(3/8)＜δ(4/8))；越靠近管中，管道翘曲变形越大，变形则会释放一部分冻胀力，故管道对管底土体的约束变小，管底土体的冻胀量较大。

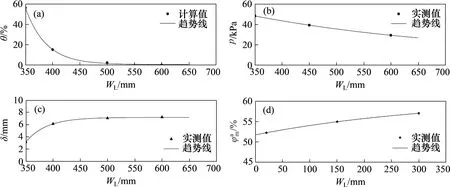
图18 4/8截面管侧各变量变化趋势Fig.18 Trends of Variables in 4/8 section on side of pipe

管侧土体的冻胀受约束的机理与管底土体相似，4/8 截面管侧各变量变化趋势，如图18 所示。从图18 可见：距离管道越远，管道对土体冻胀的约束越小，土压力越小，冻胀越大，平均含水率越大。试验结束后管底很难直接打孔取样，因此，管底的含水率无法得到，但根据以上各变量之间的关系可推断出管底冻土区的平均含水率越靠近管端越小，越靠近管中则越大。总体而言，土压力越大，意味着冻胀力或约束力越大，则约束率越大，冻胀量越小，平均含水率越小，水分迁移量越小。

3.3 管土模型的选择

在土与结构相互作用问题的分析中，土的力学特性受种种因素，包括土颗粒、结构组态、含水率、饱和度和渗透性等的影响，这些因素促使土的应力与应变现象呈现明显的非线性、不可逆以及随时间变化特征。图19 所示为不同管土相互作用模型的简化图。通常假设土介质为弹性体，并通过构建力学模型或数学关系来描述，最具代表性的理论是Winkler 地基梁模型[32]，如图19(a)所示；假设土介质每一点处的表面位移y与作用在该点处的压力p呈正比，近似由一系列近距离弹簧单元体现，即

式中：k为弹性地基系数。对于冻土地基而言，其力学特性相较于融土更为复杂，如图19(b)所示，且已有试验及理论验证在外荷载(或约束体)作用下，力与变形关系呈负相关[33]，即

式中：η为冻胀率；ηm为最大冻胀率；α为与土体性质有关的系数。在通常情况下，冻胀变形δ以冻胀率η的形式体现。在传统模型中，冻土体的抵抗作用力与变形呈正相关增大，缺点在于传统模型不仅忽略了邻近各点的应力和位移的影响，而且没有合理地体现两者之间呈负相关衰减的协调变化关系。显然，简化的弹性体并不能合理地描述冻土的力学特性。

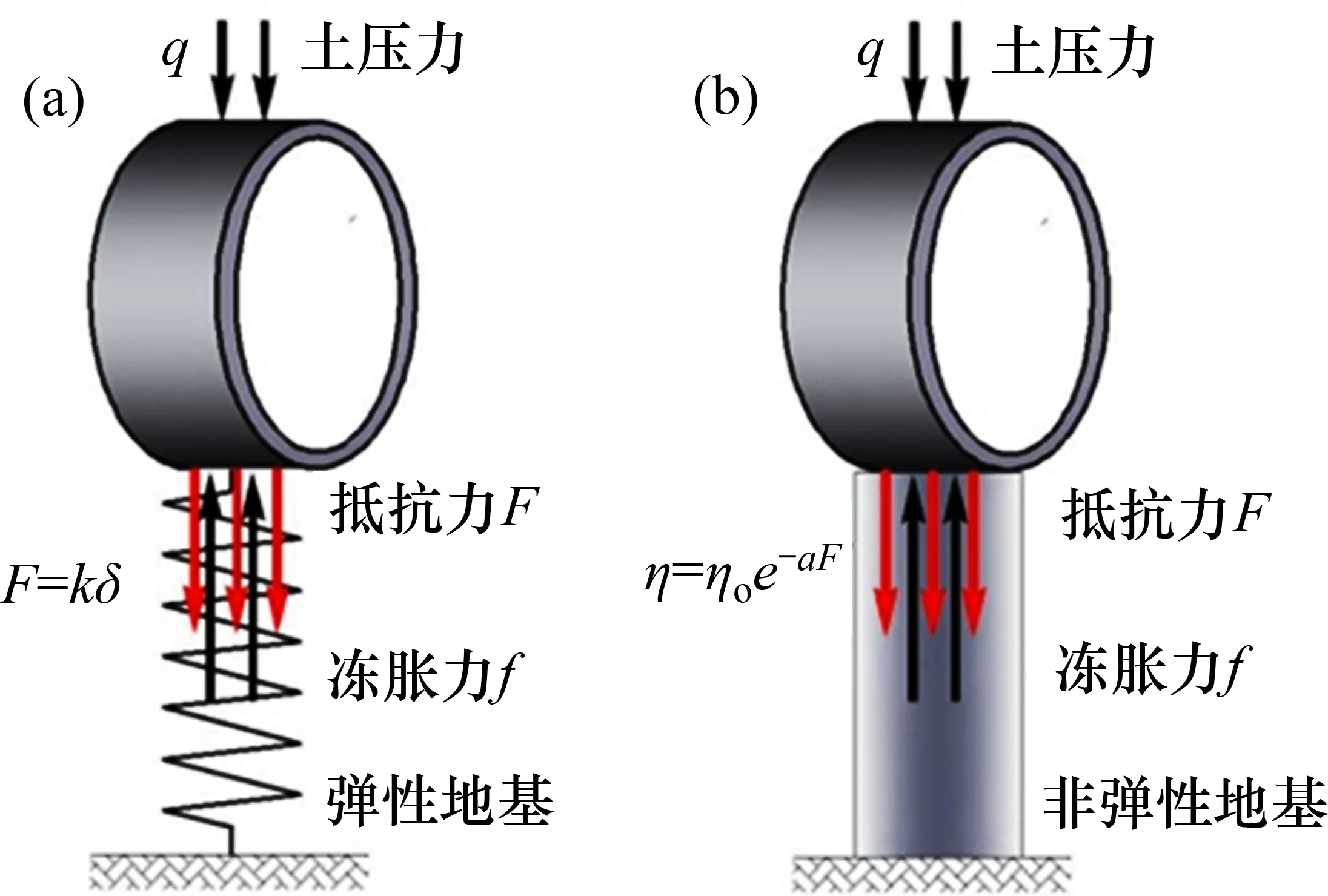
图19 不同管土相互作用模型的简化Fig.19 Simplification of different pipe-soil interaction models

冻胀现象可描述为一种土体的本构关系，到目前为止，有许多可选取的冻胀模型，但无论何种模型，在考虑有约束或荷载作用条件时的冻胀发展规律时，确定各类变量(包括约束力或冻胀力、约束变形或冻胀量、冻结速率、冻结深度和水分迁移量等)之间的逻辑关系是决定土体冻胀对管道作用分析的关键。此外，将管道与土体在冻胀条件下的相互作用效果转化为1 种合理的数学模型，体现土体内部温度梯度、含水率或含冰量，以及管道的性质(埋深、油温、流速、内压、管材和管端控制方式等)在管土相互作用过程中的相互影响关系，尚需更具体的试验进行验证。

由于试验条件的限制，本次试验的缺陷在于不能理想地模拟现场大型工程管道的冻胀问题，因此，在此后的研究中，需要进行更大且相似度更精确的模型试验或场地原位试验，并与理论相结合以建立一套合理的管土受力分析模型。