动态演化下的无标度网络生成算法
2020-06-04郑波尽代航胡丽君孙爽
郑波尽,代航,胡丽君,孙爽
(中南民族大学 计算机科学学院,武汉 430074)
真实世界中的网络无处不在,这些网络可以通过复杂网络理论来描述,其中包括www,Internet万维网,科学协作网络和全球机场网络等[1].许多实验数据表明,真实网络可以表现出无标度特性,例如,网络节点度的分布满足幂律分布[2],即大多数节点是低度节点,少量节点是高度节点.为了解释这一现象,1999年BARABSI和ALBERT[3]提出了无标度网络的生成模BA模型[3,4],该模型能采用优先连接机制[5],网络规模随着时间的推移不断增大,新节点的加入会优先连接到高度节点,能保证生成幂值近似为3的无标度网络.
然而,许多现实世界中的网络并不是单一规模的扩张,而是动态演化的,主要体现在三个方面:增加链路和节点,删除链路和节点,或节点之间链路的动态改变.例如,可以将用户聊天软件的联系人作为网络中的节点,将联系人列表中的好友作为链接来构建一个网络.尽管软件联系人的容量是一定的,但该网络仍然是一个不断发展和不断变化的网络,其中的变化包括:新联系人的添加(包括节点和链接),一些不常用联系人的删除(节点删除的同时链接同样被删除).蛋白质网络[6]也是一个不断进化的网络,当基因转录或发生突变时,同样存在节点和链接的添加和删除.
学者们为了更好地模拟出真实网络的演化模型,于是在演化过程中加入出生率和死亡率等参数来建造一个动态的演化环境,其中,SHI等[7]借鉴BA模型的演化机制,提出一种网络模型可以添加和删除链接和节点,来动态地模拟真实网络的演化情况,最终结果显示网络的结构仍具有无标度特征,并揭示了网络演变成无标度网络的过程;但是,删除和增加机制并非是随机的,其过程等价于传统的BA模型.VURAL等[8]发现网络的演化表现为新节点和边的随机添加,导致网络依赖的结构发生变化,从而不再是无标度网络;FENG等[9,10]在确定了网络构建机制的基础上,对基于生死过程的网络模型进行演化分析,最终通过对网络结构的分析,表明该模型能生成无标度网络;但是,其生死过程并非一个随机过程.在随机性的干扰下,上述网络模型都等价于传统的BA模型.
随机地增加和删除网络中的节点会导致上述模型不能生成无标度网络.真实网络是动态演化的,随着时间的增长,网络的大小和结构不断地发生着变化,随机性非常强,例如,节点死亡后会被移出网络,当多个高度节点死亡时,与这些节点相连的边都会被删除,从而破坏网络的无标度特性;同样,新生节点的随机加入也会造成网络的结构和规模发生变化.
在随机增加和删除节点之后,为了能保证网络是无标度的,本文采用优化模型的思想[11-15],提出一种动态演化下的无标度网络生成算法(SFNGA),该算法基于边度优化的多目标优化策略,在演化过程中,即使以随机方式增删节点,只要不停地优化网络的边度,使之边度最大化,就能保证网络的结构一直具有无标度特征.本文将对边度优化这一核心概念进行论述,并在数学理论和实验分析的基础上验证其正确性.
本文的组织结构如下:第一节将对动态演化下的传统模型进行分析,说明传统模型不适合随机性很强的动态演化;第二节详细介绍本文所提出的SFNGA算法,以及所采用的边度优化策略;第三节对本文提出的算法进行代码实现,并对结果进行分析;第四节对本文进行总结.
1 动态演化中的BA模型
为了验证传统模型在动态演化中的演变情况,以传统的BA模型为例,作动态演化分析.在演化过程中加入出生率和死亡率来模拟动态演化特征,同时为了保证随机性,新生节点采取随机加入的方式,并不遵从优先连接机制.出生节点的随机加入和死亡节点的删除会很大程度地改变网络的结构.因此,需对加入出生率和死亡率后的网络模型进行长时间的演化,并对演化结束后的网络结构进行表征分析.
实验条件如下:网络大小为N=1000,出生率Birth_Pi= 0.005,新生节点计算公式为N·Birth_Pi,即每次新生节点个数为5;死亡率Death_Pi= 0.005,死亡节点计算公式为N·Death_Pi,即每次死亡节点个数为5,网络中死亡的节点都是随机选择的;出生和死亡的周期为T= 10,即每演化10次进行一次出生或死亡操作;总演化时间Time= 10000.
该演化算法的伪代码描述如下:
Input:N,BP,DP,T,Time;
Initialize a BA networkG(A);
fori=1 toTimedo
ifi%T==0 do
BirthandDeath(G(A),N,BP,DP);
end if
end for
为了保证演化过程中网络规模的变化不影响实验结果的分析,假设出生率=死亡率,进行10000次的动态演化后,对节点度的概率分布做双对数表征,判断其结构的变化.实验结果如图1所示,均为度的概率分布和网络的拓扑图,其中图1(a)为演化前的网络节点度的概率分布图和网络拓扑图,很明显,演化前度分布服从幂律分布,并且网络拓扑表现出无标度特征;图1(b)为演化后的网络节点度的概率分布图和网络拓扑图,可以看出演化结束后,高度节点的数量相比演化前有很大程度的降低,节点度的概率分布并不服从幂律分布,并且从网络的拓扑图可以看出,很多节点从网络中脱离开来,说明新生节点和死亡节点导致网络结构发生了很大的变化.所以传统的BA模型并不能在动态演化中维持网络结构不变,不能避免随机性的干扰.
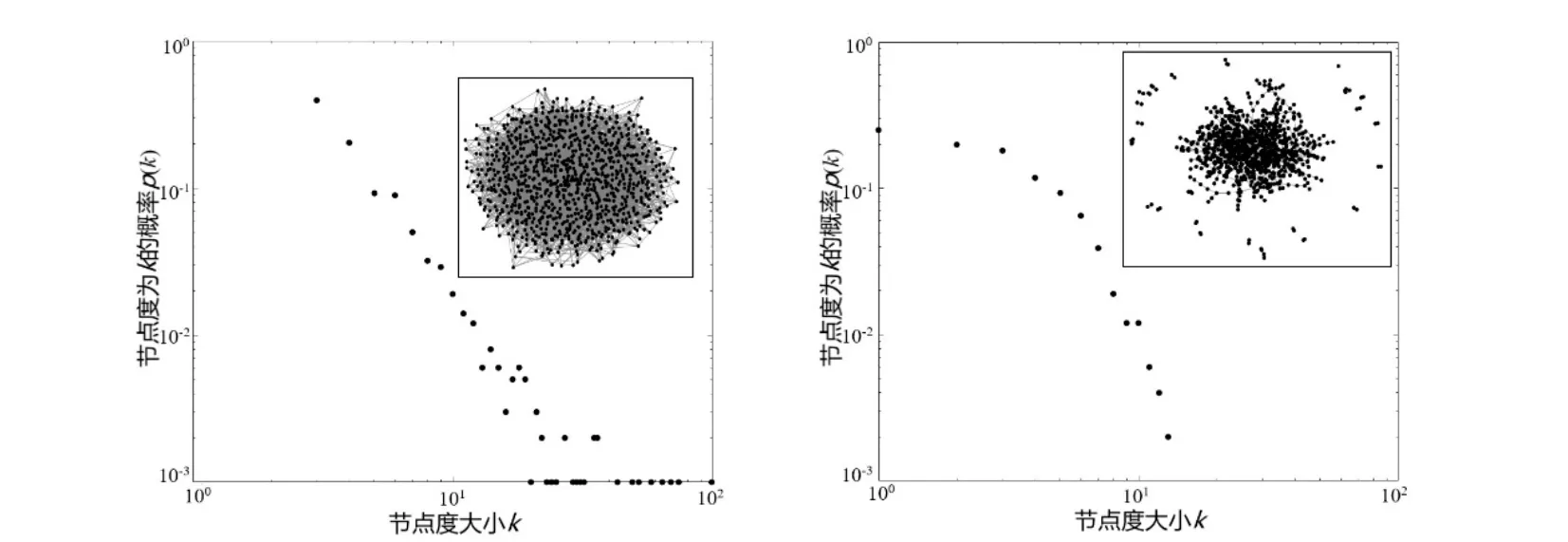
(a)演化前 (b)演化后
2 SFNGA算法
在随机性的干扰下,传统的演化模型不能生成无标度网络.为了抵抗随机性的干扰,本文基于边度优化的多目标优化策略,来得到无标度网络.
2.1 边度的定义

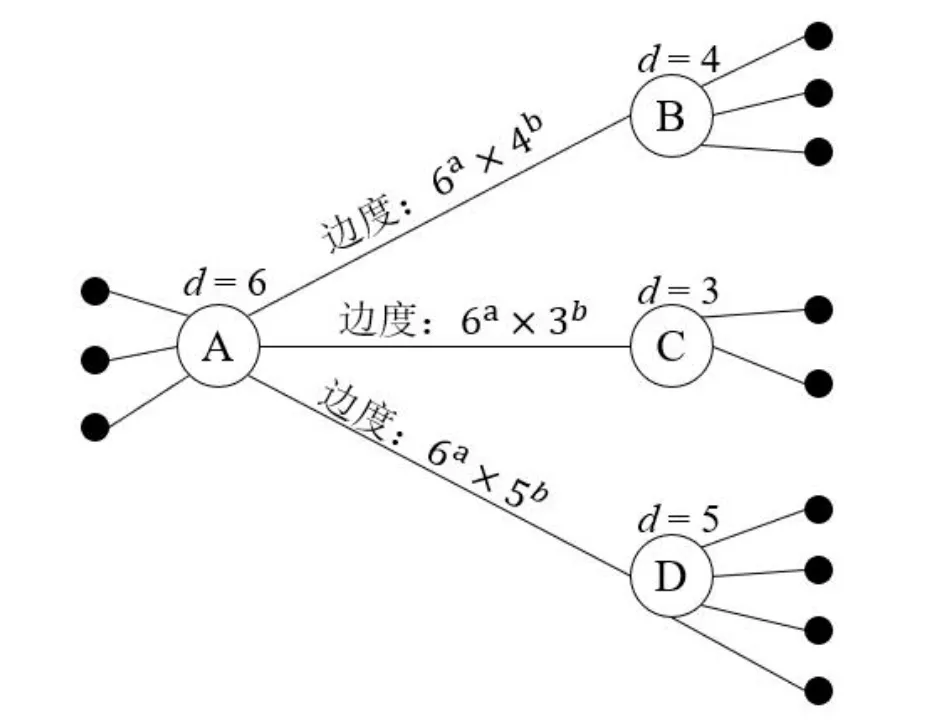
图2 边度的描述
2.2 边度优化策略
根据边度的定义,将优化模型描述为:一个连通的无向网络使其网络中节点的总度不变,使其网络的边度之和最大化.在网络的随机演化中,使网络朝着最大化边度这一目标优化.其数学模型可以表示为:
(1)
其中,A是网络变量;F(A)是网络的边度;N是网络的总节点数;xi(A)是网络中节点i的度;函数δij(A)表示节点i和节点j之间是否存在连接,如果存在值为1,否则值为0;a和b是非负常量.
无标度网络的度分布满足幂律分布,随机选取一个节点,它的度d正好是自然数k的概率满足P(k)~k-γ.于是,将网络中节点的度看成随机变量,将公式(1)中的xi看成随机变量,同时假设xi≈xj,于是:
其中xi表示第i个节点的度,并满足xi=C(X),所以公式(1)可以近似为:
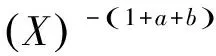
令γ=1+a+b,可以得到P(X)=CX-γ+δ,δ为一个常数.当C为一个常数时,该公式满足无标度网络的幂律分布公式,度分布指数为γ,因此,最终得到的网络是无标度网络.
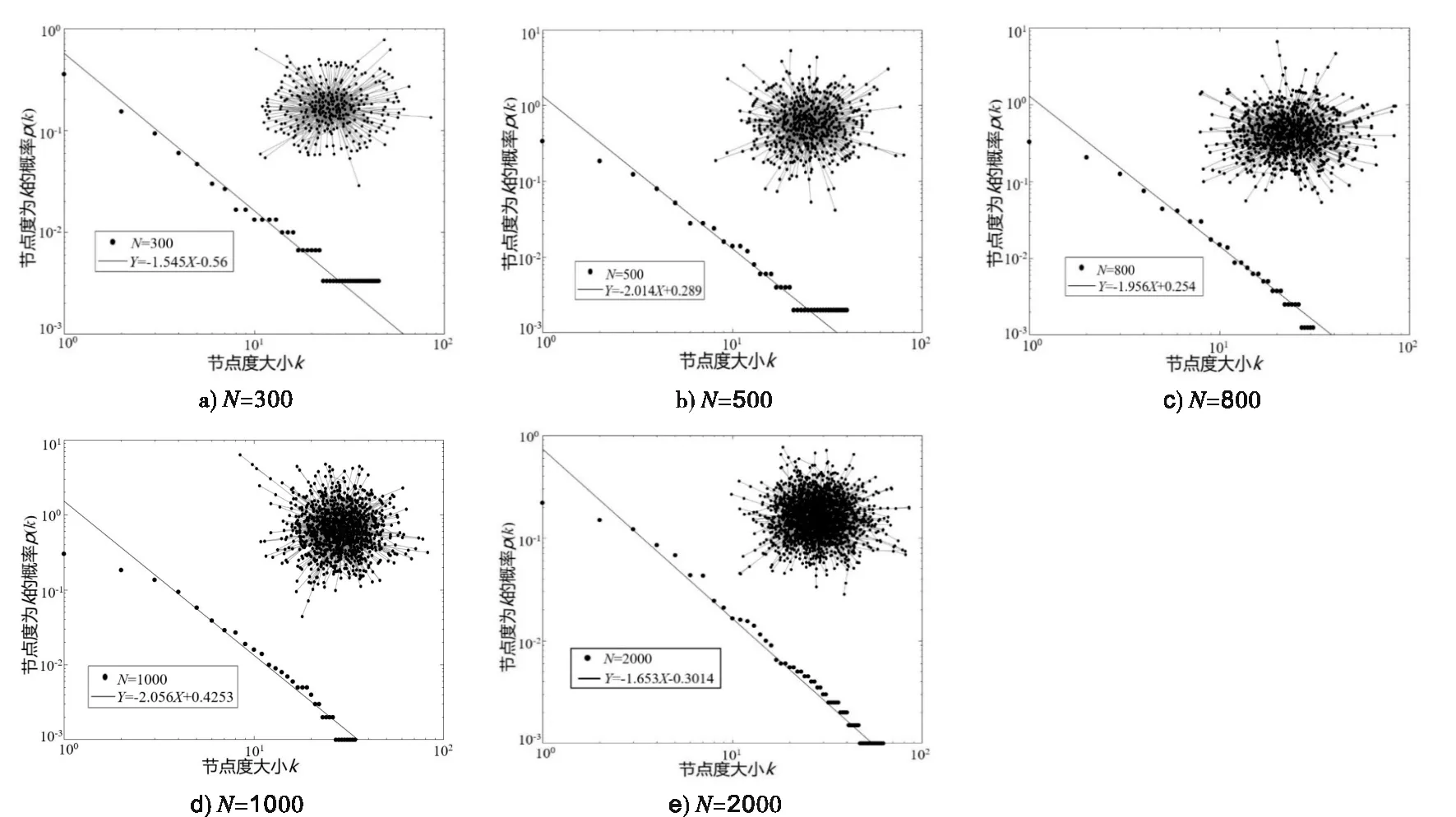
随机网络通过控制网络的总度不变,不断优化网络中节点的连边,使网络总边度最大化,从而达到由随机网络演化成无标度网络的目的.首先,初始化一个随机网络G(A),这个网络的总度为n(n为固定值),网络总的边度为edge_degree_sum1;然后,随机删除网络中的一条边并随机连接一条边,此时,网络发生改变,再次计算网络总边度为edge_degree_sum2;如果edge_degree_sum1 图3 边度优化方式 SFNGA算法采用边度优化策略,以用户给定的网络节点数、出生率、死亡率、出生和死亡的周期、优化次数和演化时间作为输入参数,最终演化结束后得到一个无标度网络.算法的主要过程为:首先根据输入的网络大小N初始化一个随机网络;然后每达到一个出生和死亡的周期就进行一次节点的删除和节点的加入,这个过程是随机进行的;出生死亡操作完成之后,进行边度的优化;演化结束便可得到一个无标度网络.该算法过程描述如下: Step1:初始化一个节点为N的随机网络,每个节点的度1≤degree≤E的网络G(A),其中N和E为常数,随机设定; Step2:出生率和死亡率的加入.设置出生率Birth_Pi和死亡率Death_Pi的数值,指定一个周期T,当达到一个周期时,网络会进行一次节点的随机删除和随机加入,每次新生的节点个数为N·Birth_Pi,死亡的节点个数为N·Death_Pi,上述参数可以随意设定; Step3:对网络G(A)进行边度的优化.首先记录网络G(A)的边度之和为edge_degree_sum1,然后随机选择网络中的4个节点(i,j,k,l),进入优化的前提条件是节点i与j之间有边,k与l之间没有边,如果不满足,则继续寻找,直到满足为止;删除节点i和j之间的边,然后将节点k与l进行连接形成一个新的网络G(B);最后,再次计算网络G(B)的边度之和为edge_degree_sum2,如果edge_degree_sum2>edge_degree_sum1,则让G(B)替代G(A),否则网络仍然为G(A).进而,还可以设置每个单位时间优化的边数来控制整个演化过程中总的优化边数,单位时间优化边数为Edge_Num; Step4:演化的总时长为TIME,当演化时间t Input:N,BP,DP,T,Times; Initialize a random networkG(A); while count G(B)=G(A); sum1 =CalEdgeDegree(G(A)); Delete an edge fromG(B); Linked an edge fromG(B); sum2 =CalEdgeDegree(G(B)); ifsum1 G(A)=G(B); count++; else continue; if count%T==0 do BirthandDeath(G(A),N,BP,DP); end if end for Output(G(A)). 根据本文2.3节对SFNGA算法的描述,可以对该算法进行代码实现,因此,只需要输入参数就可以得到指定规模的无标度网络.为了验证算法的正确性,分别输入表1中所设置的参数来生成指定的网络,其中,BP表示出生率,DP表示死亡率,E表示每次优化的边数,T表示出生和死亡周期,Time是演化的时间.为了避免网络规模影响实验结果,就需要控制每个周期T内出生节点个数等于死亡节点个数,即BP=DP.演化结束之后分别对生成的5个网络进行分析. 本文分别对表1中的5个网络进行10000次动态演化,演化结束后对网络所有节点的度作概率统计,并将统计结果用双对数表征,对所有网络的结构作拓扑分析.如图4所示:每个网络的双对数图中都包含该网络的结构拓扑图,可以看出,网络大小为300、500、800、1000和2000的幂指数γ分别为1.545、2.014、1.956、2.056和1.653,符合无标度网络的幂率特征;网络拓扑图呈现出低度节点分布在最外围、度越高的节点逐渐向网络内部聚集的现象,其中,网络中绝大多数为低度节点,只有少量高度节点在网络内部.综合以上分析可知,演化的最终结果都是无标度网络. 表1 数据参数 图4 实验结果图 在动态演化下,出生率和死亡率的加入往往会改变网络的结构特征,节点的随机删除和新生节点的随机加入会破坏无标度网络的网络结构.本文提出动态演化下的无标度网络生成算法SFNGA,该算法在动态演化中仍能保证网络结构不受出生率和死亡率这些随机因素的影响,保证最终生成的网络为无标度网络.同时该算法能根据用户给定的网络节点数、出生率、死亡率、出生和死亡的周期、优化次数和演化时间作为输入参数,生成一个指定大小的无标度网络,实验证明了该算法的正确性.它可用于疾病传播、舆情传播、人工道德网络建模等领域.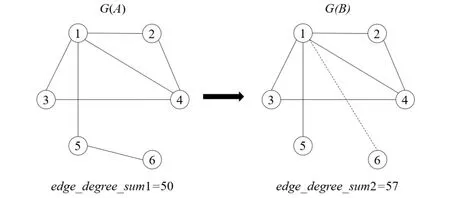
2.3 算法描述
3 实验仿真

4 结论
