Electrically tunable Goos-Hänchen shift in Dirac semimetal

CAO Zhenzhou,XIAO Zhiwei, WANG Guofei

(College of Electronics and Information, Hubei Key Laboratory of Intelligent Wireless Communications, South-Central University for Nationalities, Wuhan 430074, China)

Abstract Goos-Hänchen(GH)shift is significant in the reflection of optical beams.Here the GH shift of the linearly polarized light incident on Dirac semimetal is theoretically and numerically investigated.Through distinguishing the real part of the dielectric function, Dirac semimetal is identified as the high and low loss dielectric response, and the metallic response.It is found that the large phase jump causes the large GH shift only in the metallic region, which may provide a strategy for infrared filtering.And in the metallic region, the TE polarized GH shifts are always positive and close to zero, while the TM polarized GH shifts accompanied by an increasing Fermi energy are always negative and only of minimal values.By electrically tuning the Fermi energy of Dirac semimetal, the dielectric function and GH shifts can be manipulated, and inversely the GH shifts can be used to measure Fermi energy.

Keywords Dirac semimetal；Goos-Hänchen effect；electrically tunable

The three-dimensional Dirac semimetals(DSMs)has conduction and valence bands overlap at isolated 3D Dirac point in momentum space, and the dispersion of energy versus wave vector is linear[1].This special band dispersion causes the quasiparticles around the Fermi energy to behave like relativistic particles, which differs with the nonrelativistic electrons in most metals and dielectrics, and makes DSM response as metal or dielectric according to the light wavelength.DSM can be regarded as a 3D analogue of 2D graphene and its Fermi energy can also be adjusting through the external electrostatic gating, but it has crystalline symmetry protection against gap formation induced by spin orbit interaction[2], which leads to a ultrahigh mobility of DSM much higher than that of graphene[3].With the superior performance, DSM are already used to realize optical switch[4], narrowband absorber[5], broadband pulse generation[6], surface plasmon polaritons[7], and plasmon-induced transparency[8].

When a light beam undergoes total internal reflection at the interface of two different media, the reflected beam deviates from the geometrically expected path and has a translation.This translation is well known as Goos-Hänchen(GH)shift[9], which has been studied for a wide range of materials, such as dielectrics[10], metal[11], metamaterials[12-14], 2D Dirac semimetal-graphene[15-17], PT-symmetric medium[18].DSM has both metallic and dielectric response depending on the light wavelength, and its GH effect will appear special features.The GH shift has potential application in chemical or biological sensor, and measurement of refraction, displacement, or surface roughness.Implementation of adjusting GH shift will expand its research field and applications.In this work, we present a mechanism of electrically tunable GH shift with the light different wavelength in Dirac semimetal.

Fig.1 Schematic of a linearly polarized light beam reflected at a Dirac semimetal layer and causing Goos-Hänchen shift Dr.

According to the real part of the dielectric function, we distinguish the high and low loss dielectric response region from the metallic response region and find the large phase jump causes the large GH shift only in the metallic region, which can be potentially used in optical filtering.Though electrically tuning the Fermi energy of DSM, the GH shift can be manipulated.And in the metallic region, the TE polarized GH shifts are always positive and near to zero, while the TM polarized GH shifts are always negative and have minimal values.

1 Theory

The configuration considered here is schematically indicated in Fig.1, which shows a beam with wave numberkincident at an angleθupon a DSM layer placed in air, wherenandddenote the refractive index and thickness of the DSM layer, respectively.The Goos-Hänchen shiftDris the distance between the lateral shifted path(solid)and the path expected by geometrical optics(dashed).For simplicity, we consider a 2D light beam with a sufficiently large beam waist(a narrow angular spectrum).The fields are supposed to be linearly polarized and invariant along thexdirection with a time dependence exp(iωt)being assumed and suppressed.The incident and reflected fields can be related to each other by a transfer matrix[19, 20]:

(1)

whereqz=(ω/c)ncosφstands for thezcomponent of the wave number in the DSM layer andcis light speed in air.For TM polarizationξ=n2, and for TE polarizationξ=1.Thus we obtain the following form for the reflection coefficients and its phase:

(2)

(3)

assuming a beam with a narrow angular spectrum, the Goos-Hänchen shift is defined by[21]:

(4)

since the DSM layer has the lossy characters for metallic and dielectric response[22], the numerical calculation of the GH shiftDrfor the reflected wave can be determined by[10]:

(5)

considering both theinterband and intraband electronic transitions, the DSM dynamic conductivityσis given by[22]:

(6)

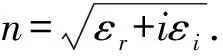
2 Results and discussions

Before analyzing the lateral shift of DSM, we analyze its dielectric as a function of the incident light wavelength.As indicated in Fig.2(a)(the parameters areEF=0.15 eV,T=300 K,εc=3,d=2 μm,θ=85°), the real part of dielectric functionεrhas a maximum value atλ≈4.2 μm.Settingεr=0, we get the wavelengthλp≈8.55 μm related to the bulk plasma frequency.DSM is called as semimetal, but its electromagnetic response, depending on the light wavelength, behaves as a metal or dielectric.Forλ>λpDSM can be viewed as a metal(εr<0), whileλ<λpDSM can be viewed as a dielectric(εr>0).Whenλ>λp, DSM has a small loss withεi<0.41 ; whenλ<4.2 μm , DSM has a high loss withεi<4.1.The reflection(R), transmission(T), and absorption(A)energy spectra[22]of the TM and TE wave with the incident angleθ=85° are shown in Fig.2(b)and 2(c).The transmitted light is weak, while the reflected light is strong and easier to be detected, in particular for the TE polarized light.Forλ>λp, the absorption of light becomes weak, because the dielectric imaginary partεibecomes small.Forλp>λ>4.2 μm , the dielectric response leads to the typical osillations in theRTAenergy spectra.Forλ<4.2 μm, the absorption corresponding to the interband electronic transitions becomes stronger, and the absorption of the TM polarized light is more obvious than that of the TE polarized light.The interband electronic transitions contribute to the imaginary part of the dielectric functionεi.Due to the gapless electron energy spectrum of DSM, the interband electronic transitions are significantly enhanced, which leads to the large loss in this region.

Fig.2 The real part εr and imaginary part εi of the dielectric functions for the DSM.The reflection(R), transmission(T), and absorption(A)energy spectra of the TM wave and TE wave.

Fig.3 The GH shifts Dr and the phases φr of the reflected waves

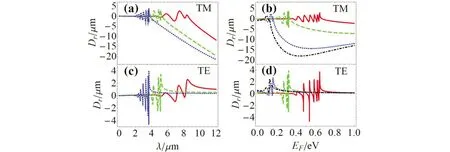
Fig.4 The GH shifts Dr as a function of the wavelength λ or the Fermi energy EF

Through electrically tuning the Fermi energy of DSM, the dielectric function and GH shifts can be manipulated.Varing the Fermi energyEFleads to increase of the GH shifts at a certain wavelength(see Fig.4(a))and the GH shifts have a minus maxmum in the metallic response region(see Fig.4(b)).In the Fig.4(a)(The parameters areEF=0.15 eV(red solid curve),EF=0.25 eV(green dashed curve), andEF=0.35 eV(blue dotted curve)in(a)and(c);λ=2 μm(red solid curve),λ=4 μm(green dashed curve),λ=8 μm(blue dotted curve), andλ=10 μm(black dashed-dotted curve)in(b)and(d).The other parameters are same as those in Fig.2.), the curves ofDrfor the TM polarization move left with increasing the Fermi energyEF, because the shorter wavelengthλachieves at the higher Fermi level.For the energy of the wavelengthλhigher than the Fermi energy, DSM shows a dielectric response, while DSM shows a metallic response at the lower energy[22], which is in accordance with our analysis in terms of the real part of dielectric functionεr.The reason is that the wavelengthλcorresponding to the Fermi energyEFis close to the bulk plasma frequencyλp, for instance,λ≈8.26 μm corresponding toEF=0.15 eV approximates toλp≈8.55 μm.The bulk plasma frequencyλp, which is obtained atεr=0 , distinguishes the metallic response region from the dielectric response region.As shown in Fig.4(b), the TM polarized GH shiftDrfor the long wavelengthλ= 8 or 10 μm has a minus maxmum at the metallic region.The minus maximal value for the short wavelengthλ=2 or 4 appears atEF>1 eV.The longer the wavelength is, the bigger the minimal value is.The longer wavelength with the proper Fermi energy is benefit for the experimental observation ofDr.As shown in Fig.4(c)and 4(d), the TE polarized GH shifts are positive and smaller than that of the TM at the metallic region, which is similar with experimental observation of GH shifts in Au[11].In an evergy-flux viewpoint, the existence of a backward energy flux causes the large negative shift for the TM plorization[28].The electrically tunable response of DSM is useful to the control of the beam, and inversely, the GH shift can be used to measure Fermi energy.

To validate the above theoretical analysis, we perform the numerical simulation of the GH shifts using COMSOL Multiphysics which is an electromagnetic softwave based on the finite element method.The waist of beam is 3λand the other parameters areEF=0.15 eV,T=300 K,d=2 μm,λ=12 μm andθ=45°.The out-of-plane field components |Ez| for TE polarization and |Hz| for TM polarization are shown in Fig.5(a)and 5(b), where the reflected red line denotes the lateral shifted path while the black line denotes path expected by geometrical optics.The GH shifts are found to be positive for TE polarization and negative for TM polarization.It is more clearly in terms of the distributions of field amplitude |Ez| and |Hz| as indicated in Fig.5(c).The simulation values are 0.058λ(TE)and-0.113λ(TM), which coincide with the theoretical results 0.061λ(TE)and-0.112λ(TM), respectively.

Fig.5 Numerical simulations of GH shifts

3 Conclusion

We have theoretically and numerically studied the Goos-Hänchen shift of the linearly polarized light incident on three-dimensional Dirac semimetal.For the different wavelength, DSM behaves as the high and low loss dielectric and metal, while the large phase jump causes the large GH shifts only in the metallic region with low-loss, which may provide a scheme of infrared filtering.In the metallic region, the TE polarized GH shifts are positive and converge to 0.1, while the TM polarized GH shifts are negative and have the minimal value at a certain value of the Fermi energy.Through electrically tuning the Fermi energy of DSM, the dielectric function and GH shifts can be manipulated, and conversely the GH shifts can be used to detect the Fermi energy.