“直线与圆的位置关系”(第1课时)教学设计及反思
2020-06-03夏乾冬
夏乾冬

【教学目标及重难点】
1.了解直线与圆的三种位置关系;
2.学会通过圆心到直线的距离d与半径r之问的数量关系判定直线与圆的位置关系;
3.用运动的观点研究问题,体会数形结合的思维方法。
【教学过程】
一、环节一:回顾旧知识点,为类比探究做铺垫
问题1:点与圆有几种位置关系?
师:前面我们学过点与圆的关系,请问点与圆有几种位置关系?
生:点在圆内,点在圆上,点在圆外。
师:每种位置关系对应怎样的数量关系?
生:点在圆内时,dr。
师:这里的d与r指什么?
生:d是点到圆心的距离,r是圆的半径。
师:很好,由点与圆的位置关系,我们可以得到d与r的关系。那么,由d与r能否推出点与圆的位置关系呢?
生:可以,因为圆的内部是到圆心的距离小于半径的点的集合,所以当dr时,点在圆外。
师:非常好!这样一来,我们就建立了形与数的关系。
二、环节二:建构问题体系,为类比探究搭梯子
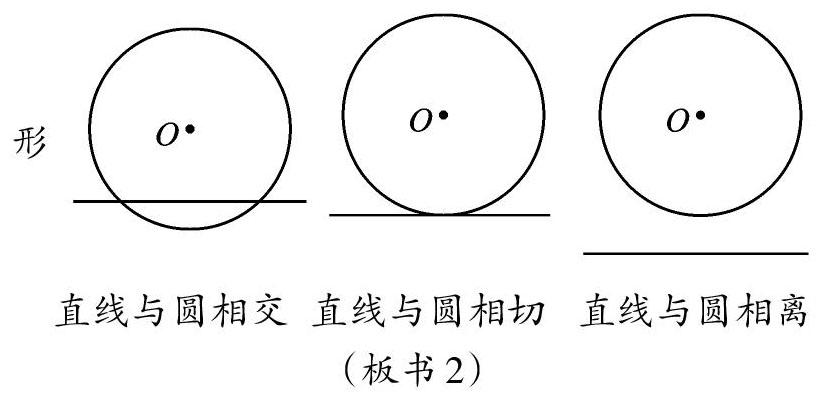
问题2:直线与圆有哪几种位置关系?请尝试画出示意图。
(学生在练习纸上画图。两分钟后,教师请几名学生到黑板上先后画出几幅直线与圆的关系示意图。)
师:大家能将这几种位置关系进行分类,并说说分类的依据吗?
生:我认为可以分为三类,即直线与圆没有交点,直线与圆有一个交点,直线与圆有两个交点。
师:我们给这三种关系起个名字——直线与圆没有交點,叫作直线与圆相离;直线与圆有一个交点,叫作直线与圆相切;直线与圆有两个交点,叫作直线与圆相交。
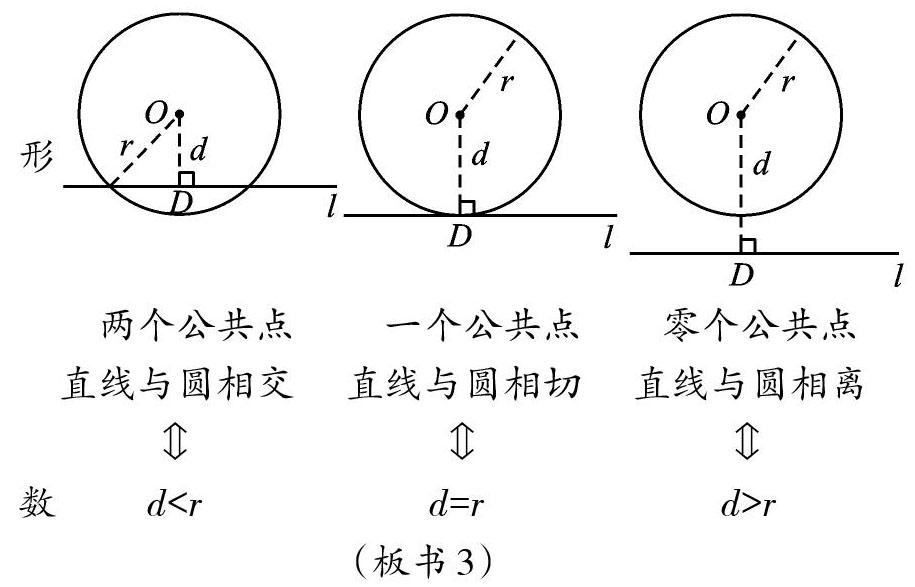
问题3:这三种位置关系中,有没有对应的数量关系呢?
师:大家能否类比点与圆的位置关系,来描述其对应的数量关系呢?
(学生思考,并在学习单上推演。)
生:我觉得跟圆心与直线的距离存在数量关系。如果把圆心与直线的距离看成d,圆的半径看成r,那么,当直线与圆相交时,dr,
师:你是如何发现的?
生:点与圆的位置关系,即点与圆心之问的距离d与圆的半径r之间的关系;直线与圆的位置关系,即直线与圆心之间的距离d与圆的半径r之间的关系。通过类比,我们就得到了相应的数量关系。
师:太棒了!
(教师在图上演示,过O点做OD⊥l,找到了d,然后对比此时的d与r的关系,在板书2的基础上形成板书3。)
问题4:点与圆的位置关系同直线与圆的位置关系有何区别及联系呢?
(教师投影问题4,请学生思考。学生小绢交流后,派代表进行展示。)
生:在点与圆的位置关系中,d是指点与圆心之问的距离,是线段;在直线与圆的位置关系中,d是指直线与圆心之问的距离,是垂线段。
生:直线l与○O的三种位置关系也可以看成点D(垂足)与○O的三种位置关系。如果点D在圆内,那么直线与圆相交;如果点D在圆上,那么直线与圆相切;如果点D在圆外,那么直线与圆相离。
师:很好!还有吗?
(学生一片沉默。)
师:如果把直线看成是由无数个点组成的呢?
(有的学生顿悟,发出“哦”的声音。)
生:直线与圆相交时,直线上的点在圆内、圆上和圆外;直线与圆相切时,直线上的点在圆上和圆外,不在圆内;直线与圆相离时,直线上的所有点都在圆外。
师:太厉害了!这位同学说出了点与圆的位置关系同直线与圆的位置关系的内在区别和联系。
(此时,学生自发地响起掌声。)
问题5:在这三种位置关系中,你认为哪一种最特殊?
生:我认为直线与圆相切时的位置关系最特殊。
师:为什么?
生:因为此时直线与圆有一个公共点,而且圆心到直线的距离与半径的关系是d=r。
师:是的,此时,这条直线叫作圆的切线,这个公共点叫作切点。说到这里,哪位同学能推测一下,后面我们会学习什么?
生:既然切线比较特殊,我觉得后面应该会学习切线的性质。
师:非常好!后面我们还会研究切线的性质和判定。那么,今天这节课我们就上到这里,下课!
【教学反思】
在本节课上,基于点与圆的位置关系这一“数学现实”,笔者首先创设情境,提出“点与圆有几种位置关系”的问题.引导学生进行复习回顾,并通过追问“每种位置关系对应怎样的数量关系”,为类比探究直线与圆的关系做好铺垫。接着,笔者继续提出问题,引导学生通过类比,探究直线与圆的位置关系,及其对应的数量关系。最后,笔者通过追问,使学生对直线与圆最特殊的位置关系产生关注,并抛出切线、切点的概念,为下节课的内容做铺垫。
除了进行问题引导教学外,笔者在本节课中还特意通过“雕塑式板书”,来记录学生思维的生长过程。所谓“雕塑式板书”,就是教师根据教学活动的进程,有意识地选择对学生思维有帮助的精髓内容进行板书。在一开始,板书可能只表达了一些零散的信息,但是,随着教学内容的推进和数学思维的深入,板书最终会呈现出一个完整的知识结构。“雕塑式板书”的时问节点能够与学生思维成长的过程同步,这是PPT所无法实现的。
总之,一堂数学课的结束,并不意味着教学内容和数学思维的戛然而止。数学课应当“收”中有“放”,通过及时的回顾总结和类比探究,使前后知识形成一个完整的体系。正如章建跃老师所言:“研究的对象在变,研究套路不变,思想方法不变,这就是数学基本思想、基本活动经验的力量。” (作者单位:江苏省南京市江宁区开发区学校)
