特殊化：儿童数学思考的脚手架

叶娟

摘 要：从特殊到一般，从具体到抽象，这是人们普遍遵循的认知规律。特殊化是儿童在解决问题的时候常常会用到的方法，是儿童探寻一般规律的起点，也是儿童数学思考的脚手架之一。在数学教学过程中，教师应关注儿童的思考过程，关注数学思想方法，让数学思考真发生。

关键词：特殊化;儿童;数学思考;脚手架

中图分类号：G623.5文献标识码：A     文章编号：1992-7711（2020）07-054-2

辩证唯物主义认识论认为：从特殊到一般，从具体到抽象，这是人们普遍遵循的认知规律。在小学阶段，当儿童面对抽象复杂的数学问题时，采用“以退为进”的策略，通过特殊的情形、简单的事例来探寻问题的结论，这是普遍存在的不容忽视的儿童们的真实的数学思考方式之一。我们称这样的思想为特殊化思想。特殊化既是一种思想，也是一种方法，是一种重要的数学思想方法。依据波利亚所说“特殊化是从考虑一组给定的集合过渡到该集合中一个较小的集体或仅仅一个对象。”特殊化在中学乃至大学的解决问题中被广泛地应用着。我们常常会听到所谓的“投机取巧”、“笨办法”、“不知道行不行”。仔细一想，其实用的就是特殊化：儿童数学思考的脚手架。

脚手架，是建筑单位为了确保各施工过程顺利进行而搭设的工作平台。本文的“脚手架”则是指在课堂教学中，教师设置的比较直观的、贴近学生思维的支点，以帮助学生从现有发展水平向潜在发展水平过渡。

一、搭建脚手架的缘起——从儿童思考中来

1.问题

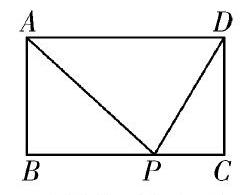
长方形ABCD的面积是24平方厘米，P是BC边上任意一点，求三角形ADP的面积。刚读完题，有学生迫不及待地问：老师，点P可以在线段BC的两个端点的位置吗？立刻，学生们的表情：惊喜、豁然开朗、期待……

五年级下配套练习中有这样一个问题：甲、乙两数都是自然数，并且甲÷乙=6，甲和6的最大公因数是（）。三个选项：A.甲;B.乙;C.6，正确答案是C。年级各班错误率均超过40%，以选B的居多，个别选A。

2.相关知识点

一个数是另一个数的倍数，两个数的最大公因数是其中较小的数。可能的错误原因分析：1.审题不清，当成求甲和乙的最大公因数了。2.题目表述较抽象，学生不清楚甲和6也是倍数关系，两个数的最大公因数是6。

3.课堂回放

师：读完题你知道了什么？

生：甲是乙的6倍。

师：是的，还知道什么？问我们什么？

生：问甲和6的最大公因数是多少。

师：你有什么要提醒大家的？

生：是甲和6的最大公因数，不是甲和乙的最大公因数。

师：很好，说说你是怎么想的？

生：由甲÷乙=6，我们可以知道甲÷6=乙，甲是6的乙倍。所以甲和6也是倍数关系，所以甲和6的最大公因数是6。（观察学生表情：有明白、也有懵圈的，的确乍听有些绕。）

师：这位同学说的很清楚，明白了吗？此处应该有掌声。

一个学生怯生生地说：我是把甲当作12，乙当作2来想的。12和6的最大公因数是6，所以我选6。（再观察学生表情：哦，这么简单？）

师：还能再举一些例子吗？

生：甲÷乙=6

12÷2=6

18÷3=6

24÷4=6

30÷5=6（依据学生回答相机板书）

36÷6=6

……

师：你发现了什么？

生：不管甲乙分别是多少，甲都是乙的6倍。

师：这叫“赋值法”，是一种特殊化的思想。这种方法可以帮助我们探索规律，在今后的学习中还会遇到。我觉得也应该给这位同学掌声。“推理法”、“赋值法”、“列举法”等等，都是很有用的数学方法，它们的背后都蕴藏着重要的数学思想。

从思维活动的方向来看，“一般到特殊”的过程是强抽象，其实际是演绎推理，这个过程比较直接，但不易理解，对思维水平要求高一些;而“特殊到一般”的过程是弱抽象，其实际是归纳推理的过程，这个过程比较直观，更贴近学生的思维水平，更容易理解。

二、特殊化方法的运用——到问题解决中去

一个问题在普遍意义上难以识别与掌握，在特殊情况下往往清楚明白。既然如此，我们何不顺应儿童的思考，从儿童最直接，最能想得到的地方开始，一步一步引导，让思考由点到线再到面，把问题理解得更透彻？

这样一个问题困扰了许多学生：“上山速度为每小时12千米，下山速度为每小时18千米，问上山下山平均速度为每小时多少千米？”（12+18）÷2=15（千米/时）这个答案是最不假思索的。然而，用特殊化赋值法一算：

总路程36千米，36×2÷（36÷12+36÷18）=14.4（千米/时）

总路程120千米，120×2÷（120÷12+120÷18）=14.4（千米/时）

总路程240千米，240×2÷（240÷12+240÷18）=14.4（千米/时）

……

正确的上山下山平均速度为14.4千米/时。

用了特殊化这个脚手架，学生不仅解决了问题，而且对这类问题认识得更加深刻。一个特殊化是特殊化，诸多的特殊化就为走向一般化提供了可能。特殊化可以快速、准确的解决问题，但不可以以偏概全。特殊化不仅可以使问题转化，而且能发现问题的解決办法，揭示问题的内在规律和探求问题的结果。罗增儒教授说特殊化是解决问题的突破口，是寻找思路的策略，是解题的方法。

特殊化原本就与学生靠得很近。求两个数的最大公因数和最小公倍数，绝大多数学生会先判断两个数是否互质，两个数是否有倍数关系，当都不符合的时候再去分解因数。用特殊化可以解决很多问题：行程问题、归一问题、平面图形面积等，不再一一举例。

特殊化可以把需要解决的问题中的问题和条件进行合理转换，拓开思路，从而解决问题，探索出结论。运用“特殊化”的关键是“过渡”，在小学数学所遇到的问题中主要有赋值特殊化、选取特定对象特殊化以及缩小范围特殊化几种，从上面的例子可以窥见一斑。

三、关注思考过程，关注思想方法——回归数学本质

特殊化是儿童数学思考的脚手架，但并不是终极目标。正如生活中我们所见的脚手架是要拆除的一般。运用特殊化，需要教师基于对目标的把握，适当引导，从而真正达到在数学思考、思维提升、发展数学核心素养的目的。

1.从儿童出发，关注思考过程

用特殊化方法算出的结果和用推理得到结论的同学是都值得肯定的。从上述例子可以看到，赋值法通过巧妙赋值，使问题数值化、直观化、简单化、特殊化，从而使问题得以很好的解决。赋值法在解题中具有广泛的应用和独特的价值。往往在缺少条件的时候，用这种方法可以帮助我们降低解决问题的难度。有种拨开迷雾见月明的效果。

每位学生的思维发展程度不同，每位同学的考虑角度不同，每位学生的元认知不同，正所谓百花齐放。我们需要尊重他们的思考，适当放大他们的想法，不能急于评价哪种方法好，哪种方法不好，更不应用褒贬之词如“聪明方法”与“笨办法”来形容。数学思想方法没有孰优孰劣之分，思考的路径不同，方法不同，殊途同归，各有优势。适合儿童的，符合儿童认知规律的方法就是好方法。坚信这样的理念与从儿童出发是一致的。俗话说不管黑猫白猫逮着老鼠便是好猫。孩子的方法值得我们研读，值得我们尊重。在解决问题时，不能太固化学生的想法，更不能用成人的思考强加给学生。从儿童出发，关注思考过程，给特殊化的儿童以特殊化。

2.从儿童出发，关注思想方法

2011版数学课程标准中提出“四基”即：基础知识，基本技能，基本经验，基本数学思想。在旧版课标的基础上增加了基本经验和基本数学思想。可见，基本数学思想的受重视程度。

每种思想方法都有其作用和数学价值。特殊化作为一种数学思想方法的存在，其价值毋庸置疑。关注不同的数学思想方法是心中有数学本质的表现，是从儿童出发的体现。

数学思考是数学核心素养形成的关键，我们需要学生有价值的思考点，设计有利于放大有价值的数学思考的问题，引导学生将这种“思考形式”内化为深层次的“数学思考”。虽然证明的过程是形式的，但对证明的理解是直观的;虽然逻辑的基础是基于公理的，但思维的过程是归纳的。为了实现这样的教学过程，我们需要更多地关心学生的思考过程，抓住数学的本质，让学生在掌握知識技能的同时，感悟数学思想，积累数学思考的经验，形成和发展数学核心素养。

（作者单位：南京市鼓楼区第二实验小学，江苏 南京210000）