DNA 非均匀功能化纳米粒子的可编程自组装行为

谷梦鑫， 张良顺， 林嘉平

（华东理工大学材料科学与工程学院，上海市先进聚合物材料重点实验室，上海 200237）

纳米级别构筑单元的尺寸效应赋予纳米粒子材料独特的电学、光学、磁学和力学性能[1]。自组装是一种“自下而上”制备纳米有序结构材料的有效手段。根据Watson-Crick 原则，互补DNA 序列可以通过氢键形成热力学可逆的碱基对，使DNA 成为纳米粒子间理想的“黏合剂”[2]。Mirkin 等[3]于1996 年将末端带有硫醇基团的DNA 链与球形金纳米粒子混合，首次制备了表面DNA 链均匀分布的纳米粒子，即DNA 均匀功能化纳米粒子。此后，研究人员利用DNA 功能化纳米粒子的自组装行为得到了线性、薄膜状、超晶格等多种超结构[4-6]。

DNA 功能化纳米粒子的自组装行为与原子间形成共价键的过程有很多相似之处，因而DNA 功能化纳米粒子被称为可编程原子等价物[7]。但是，DNA 均匀功能化纳米粒子难以控制其形成杂化碱基对的数量和方向，在制备具有特殊结构的纳米粒子材料方面具有一定局限性。近来，仅在表面特定位置分布DNA 链的纳米粒子，即DNA 非均匀功能化纳米粒子为精确控制自组装结构提供了新方法[8-11]，纳米粒子的结构可设计性和序列可编程性使其自组装行为更加复杂。定量描述DNA 非均匀功能化纳米粒子的自组装动力学行为对获得结构可控的自组装体具有十分重要的意义。

计算机模拟在示踪粒子运动轨迹、阐明实验机理等方面具有极大优势，已成为研究纳米粒子自组装行为和结构的重要方法。本文以DNA 非均匀功能化纳米粒子为研究对象，通过粗粒化分子动力学模拟纳米粒子可编程自组装过程，探索自组装的结构与动力学。

1 模拟方法

基于Travesset 课题组[12-13]发展的DNA 均匀功能化纳米粒子的粗粒化模型，本文建立了DNA 非均匀功能化纳米粒子模型（如图1 所示）。设球形纳米粒子的半径（Rs）为3σ，其中σ 为模拟的长度约化单位（σ =2.0 nm）。3 条DNA 链等间距地锚定于球面赤道位置。每条DNA 链含有中性部分（Spacer）和DNA 黏性端（Linker），分别含有ns和nl个粗粒化珠子。黏性端中1 个粗粒化珠子代表3～7 个碱基；若nl=3 时，粗粒化DNA 链的黏性端相当于序列长度约为15 个碱基的寡聚核酸。模型中，DNA 链的尺寸与纳米粒子直径相近[1,14,15]。为了确保DNA 链完全互补，黏性端序列分别设置为-ACK 和-FGT。需要说明的是A-T 和C-G 为互补碱基对，而K-F互补碱基对的引入是为了防止DNA 链自杂化。含有-ACK 序列的功能化纳米粒子标记为V 型纳米粒子；相应地，含有-FGT 序列的纳米粒子标记为W 型纳米粒子。

图 1 （a）DNA 非均匀功能化纳米粒子的粗粒化模型；（b）互补DNA 链的黏性端杂化示意图Fig. 1 （a）Coarse-grained model of non-uniformly DNA-functionalized nanoparticles;（b）Hybridization between complementary DNA strands containing ns spacer beads and nl linker beads

模型中，相邻珠子的键连作用为谐振子势，包括键长作用势（Ubond）与键角作用势（Uangle）

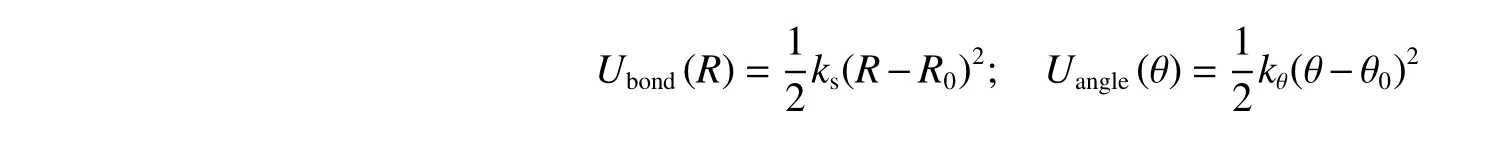
式中，R 表示2 个粗粒化珠子的间距，其平衡值R0= 0.84σ，系数ks= 330ε/σ2（ε 为能量约化单位）。θ 表示3 个连续粗粒化珠子之间的角度，其平衡值θ0= π，系数kθ= 30ε。互补碱基对粗粒化珠子间的非键相互作用由Lennard-Jones 势能表示：式中，作用强度εbp= 10ε，截断半径Rc= 2.75σ。其他粗粒化珠子之间的相互作用为纯排斥力，由Weeks-Chandler-Andersen 势能表示[16]：此处Rc=21/6σ。

分子动力学模拟在正则系综（NVT）下进行。体系一共含有N=200 个DNA 非均匀功能化纳米粒子。V和W 型纳米粒子的个数分别为NV和NW（N =NV+NW），化学计量比（f）定义为f =NV/NW，f≥1。模拟盒子满足周期性边界条件，其尺寸为L×L×L。DNA 功能化纳米粒子的体积分数（ φ ）定义为 φ ≡4πN(Rs+Re)3/3L3，其中Re是DNA 链特征尺寸， Re=σ(ns+nl)1/2。分子动力学模拟的时间步长（t）设置为t = 0.001τ，其中τ 为时间约化单位。为了确保体系达到平衡状态，每次分子动力学模拟约进行4×108步。

2 结果与讨论

2.1 化学计量比对自组装结构的影响

在分子聚合反应中，多官能度单体聚合可以得到非线性拓扑的聚合物，如支化和网络状聚合物。通过调控单体的化学计量比可以得到不同的结构。类比于多官能度单体的分子聚合反应，当纳米粒子功能化3 条DNA 链时，每一个通过DNA 序列杂化加入到聚集体中的纳米粒子将带来2 个新的“生长点”（DNA 黏性端）；在此驱动下，游离的纳米粒子自组装形成支化和三维网络状超结构[17]。同高分子链拓扑结构的调控机制类似，自组装超结构的拓扑依赖于V 和W 型纳米粒子的化学计量比f。

为了证实上述推测，构建了不同数目的V 和W 型纳米粒子体系，并进行了分子动力学模拟。V 和W 型纳米粒子的数目之比（NV/NW）分别为100/100、125/75、150/50 和170/30，对应的化学计量比分别为1.0、1.7、3.0 和5.7。图2 展示了不同化学计量比之下，纳米粒子通过互补DNA 序列杂化所形成的自组装超结构。当f=1.0 时，在互补DNA 序列杂化的引导下，纳米粒子自组装形成三维网络状超结构。需要说明的是，此网络状超结构在各个方向上是贯穿的，为逾渗网络。随着f 的增大，过量的DNA 序列参与杂化的可能性减小，网络状超结构变稀疏（f =1.7），进而转变为支化超结构（f =3.0）。当f=5.7 时，数量较少的W 型纳米粒子完全被V型纳米粒子包围，只能够形成离散分布的小聚集体；大部分V 型纳米粒子仍处于游离态。由此可见，通过改变体系的化学计量比，DNA 链非均匀功能化纳米粒子从三维网络状超结构转变为支化超结构，甚至是离散分布的小聚集体。

为了定量表征纳米粒子自组装结构，我们构建了自组装结构的几何模型（图3（a））。在分子动力学模型中，DNA 链有一定刚性，并且等间距地锚定于球面赤道位置。通过互补DNA 序列杂化（实线），最邻近纳米粒子间距离为r0，即为典型“键合”距离[18]。次邻近纳米粒子间距离为（虚线）。纳米粒子自组装结构特征可通过粒子间径向分布函数g（r）表征，其中径向分布函数特征峰的位置和强度可以表征自组装超结构中纳米粒子之间的相对位置及其分布[19-22]。

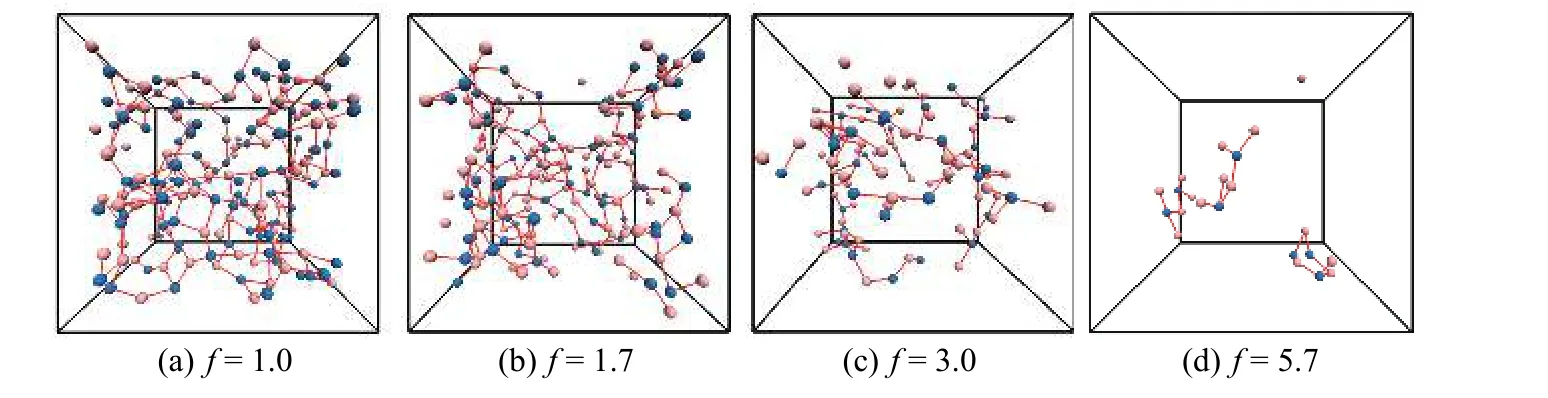
图 2 化学计量比f 对自组装超结构的影响（图中只显示通过互补DNA 序列杂化所形成的最大纳米粒子超结构，红线表示由互补DNA 序列杂化形成的纳米粒子间连接）Fig. 2 Effect of the stoichiometric ratio on the superstructure of nanoparticles（Note that only the largest superstructures are shown; Red lines represent the connectivity between various nanoparticles through the hybridization of complementary DNA strands）

图3（b～d）展示了不同化学计量比f 和中性部分长度（即中性珠子个数，ns）下的径向分布函数g（r）。图中虚线从左至右分别对应于特征峰的理论预测位置r/r0为1 和当f=1.0 时，带有互补序列的纳米粒子相互连接形成三维网络状结构，纳米粒子间相对位置关系符合图3（a）的预测（如图3（b）所示，在r/r0为1 和处特征峰的峰值较大，峰形较为显著）。随着f 的增大，体系中存在多个松散分布的支化聚集体，使得特征峰强度减弱（图3（c））。当ns增加时，径向分布函数g（r）的特征峰进一步减弱（图3（d））。此外，当ns=4 时，径向分布函数g（r）在r/r0= 1 之前没有明显的峰（图3（c））；而当ns= 10 时，径向分布函数g（r）在r/r0= 1 之前出现多个明显的峰（图3（d））。其原因是，较长DNA 链占据的空间较大，使得相连的V 和W 型粒子间空隙变大，从而形成互穿支化结构[18]。

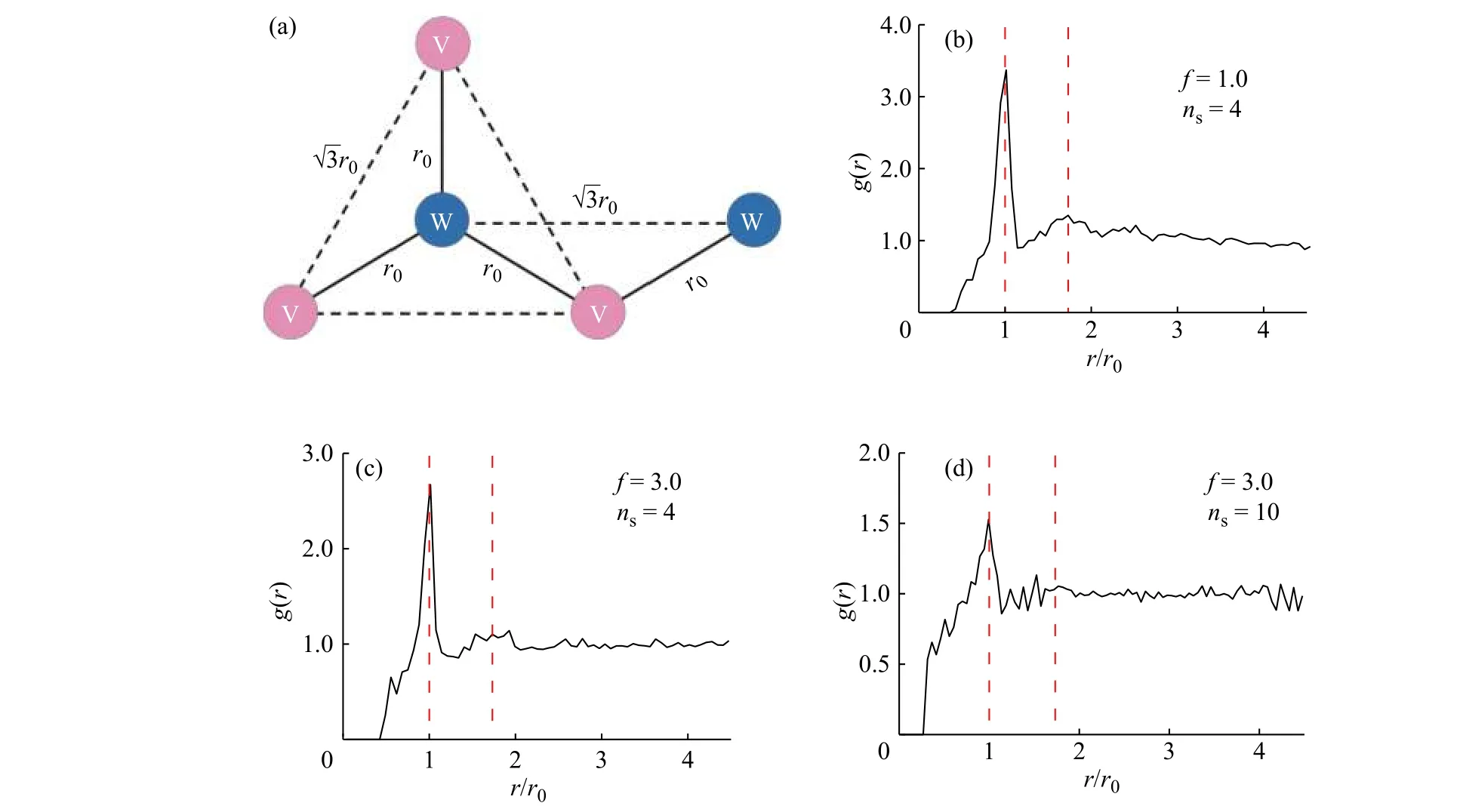
图 3 （a）纳米粒子自组装结构的几何模型（实线为通过互补DNA 序列杂化所形成的纳米粒子间连接，虚线连接的是次邻近纳米粒子）；（b～d）不同化学计量比（f）和中性部分长度（ns）下纳米粒子径向分布函数g（r）（约化温度T *= 0.90，纳米粒子体积分数φ = 0.10）Fig. 3 （a）Geometrical representation of self-assembled superstructures of nanoparticles（Solid lines denote the connectivity between nanoparticles, and dashed lines denote the connectivity of nanoparticles with sub-nearest distance）；（b—d）Radial distribution function g（r）of nanoparticles for a range of stoichiometric ratios （f） and the lengths of spacer（ns）（The reduced temperature is set as T *= 0.90,and the packing fraction is set as φ = 0.10）

2.2 化学计量比对自组装动力学的影响

化学计量比不仅影响自组装超结构，还会改变自组装动力学。为了定量描述自组装过程中聚集体的生长过程和DNA 黏性端的杂化程度，模拟中统计如下2 个物理量：聚集体数量（Na），它表示包含2 个及以上纳米粒子的自组装超结构数量；碱基对数量（Nh），它表示通过互补DNA 序列杂化生成的碱基对数量。图4 是聚集体数量和碱基对数量随时间的变化曲线。在给出的化学计量比之下，Nh随着模拟时间的延长而增加，最终达到平衡值。Na则随模拟时间的延长表现出非单调变化。在f =1.0、1.7、3.0 时，Na先增加后减小，直至达到平衡值。这说明在自组装早期，纳米粒子先形成较小的聚集体；随后，在聚集体外围DNA 黏性端的引导下，小聚集体之间相互融合形成更大的聚集体，甚至网络状结构，导致聚集体数量下降。当f =5.7 时，过量的V 型纳米粒子分布在聚集体外围，消耗并屏蔽了非过量的W 型纳米粒子，使得聚集体数量变化不再显著。

化学计量比还影响了自组装结构的动力学行为。本文考察了纳米粒子的均方位移（MSD）以及最大聚集体所包含的纳米粒子数目与纳米粒子总数之比（η）。图5（a）对比了不同化学计量比下的均方位移随时间的变化趋势[12,23]。图5（b）为自组装体系中η 随时间的变化曲线。当f =5.7 时，体系中只能形成非常小的聚集体，同时存在未发生DNA 序列杂化的纳米粒子；纳米粒子的MSD 接近于线性增长。随着f 的减小，MSD 曲线在经历自组装初期的快速增长后，增幅出现不同程度的减弱。特别是，在f =1.0 时，自组装时间t 超过5×104τ 之后，MSD 达到平衡，不再增加。由图5（b）可知，此时纳米粒子自组装形成一个大的聚集体（网络状结构），导致纳米粒子扩散缓慢。

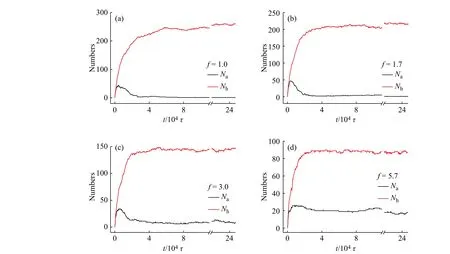
图 4 不同化学计量比下聚集体数量（Na）与DNA 杂化碱基对数量（Nh）随时间的变化曲线（约化温度T *= 0.90，纳米粒子体积分数φ = 0.10）Fig. 4 Temporal evolution of numbers of aggregates （ Na） and numbers of hybridizations （Nh） at various stoichiometric ratios （The reduced temperature is set as T *= 0.90, and the packing fraction φ = 0.10）

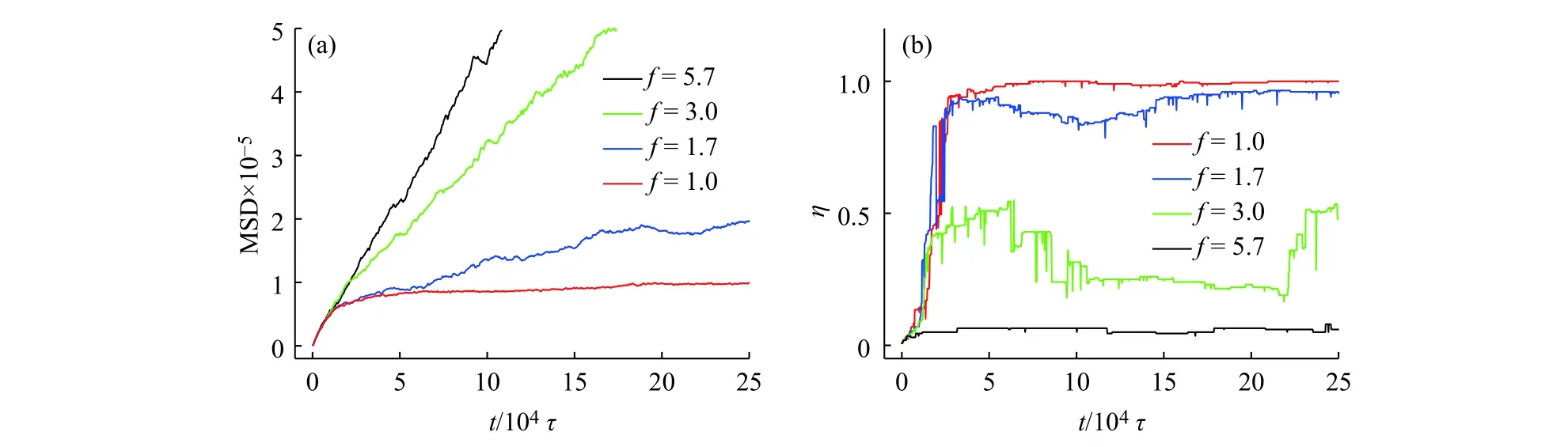
图 5 不同纳米粒子化学计量比下（a）MSD 和（b）η 随时间的变化曲线（约化温度T *= 0.90，纳米粒子体积分数φ = 0.10）Fig. 5 Effects of stoichiometric ratios on （a）mean square displacement （MSD） and（b）the nanoparticles’ fraction of largest aggregates （η） in terms of the assembly time（The reduced temperature is set as T *= 0.90, and the packing fraction φ = 0.10）

3 结 论

本文构建了DNA 非均匀功能化纳米粒子的粗粒化模型，采用粗粒化分子动力学方法模拟了纳米粒子的可编程自组装过程，研究了化学计量比对自组装行为的影响。模拟发现：通过改变体系的化学计量比，DNA 功能化纳米粒子从三维网络状超结构转变为支化超结构；构建了纳米粒子结构的几何模型，正确地预测了纳米粒子之间的相对位置及其分布；化学计量比显著地改变自组装动力学行为和自组装结构的动力学行为。