基于BAS-BP神经网络的异步电机电流预测

党盈伟，刘广璞，郭彦青，杨韩峰，林炳乾

(中北大学机械工程学院，山西 太原 030051)

管排锯要求锯切出的钢管切面质量好且切口光滑整齐[1],由异步电机控制的锯片在锯切时对钢管有很大的作用力。当锯片进行锯切时，锯片与钢管在高速、强压的条件下会产生很大的锯切力，造成锯片局部发生断裂和磨损，导致在线监测的电机电流值发生很大波动，从而影响管排锯的正常锯切。因此，对锯切中的异步电机电流进行初步预测是有必要的。近年来，国内外对电流预测的算法很多，其中广泛使用的算法有灰狼算法(GWO)、遗传算法(GA)、模拟退火算法(SA)等[2-4]。这些算法已经被应用于现代工业生产的很多领域。

天牛须搜索(beetle antennae search,BAS)算法是一种新型生物启发式智能算法，该算法与粒子群算法、遗传算法等智能算法相似。BAS算法也叫作甲壳虫算法，其思想源于天牛觅食行为，天牛有两根触角，当天牛周围有食物时，它的两根触角会根据气味强度的高低进行搜寻。BAS算法的优点是只需要搜索单一个体，不需要知道目标函数的具体形式，便可实现高效寻优，搜索速度快，运算量小，且算法计算过程简单，迭代次数较少，不会受到太多的初始条件限制。许多学者将该算法应用到各个领域。王甜甜等[5]首先将风暴灾害数据进行预处理，然后利用建立的BAS-BP模型对灾害数据进行分析，该模型能够较好地对风暴灾害所造成的经济损失进行预测和评估。刘涛等[6]将改进的天牛须算法-优化极限学习机(BSAS-ELM)与极限学习机(ELM)及支持向量机(SVM)进行对比，利用改进的BSAS-ELM预测模型对热泵能耗分别进行单步和多步预测，结果显示，该预测模型的预测精度有了显著的提高。卢光辉等[7]对BAS算法进行改进，提高了算法的稳定性，并将该算法用于求解分布式电源选址定容问题。以上研究成果为异步电机电流的预测提供了丰富的理论基础，本文利用BAS-BP神经网络模型，实现对异步电机电流的初步预测。

1 数据采集与记录

在管排锯生产现场，主锯的异步电机与锯片如图1所示。异步电机控制锯片高速旋转，而伺服电机控制锯切速度，锯片以平稳的旋转速度垂直向下对钢管进行锯切。通过上位机(WinCC)对两台主锯的异步电机电流值实时在线监测，然后将监测电流值归档整理，再由MATLAB软件进行预处理，将处理后的样本数据作为BAS-BP神经网络模型数据。两台主锯电机的电流值如图2和3所示。

图1 管排锯主锯设备

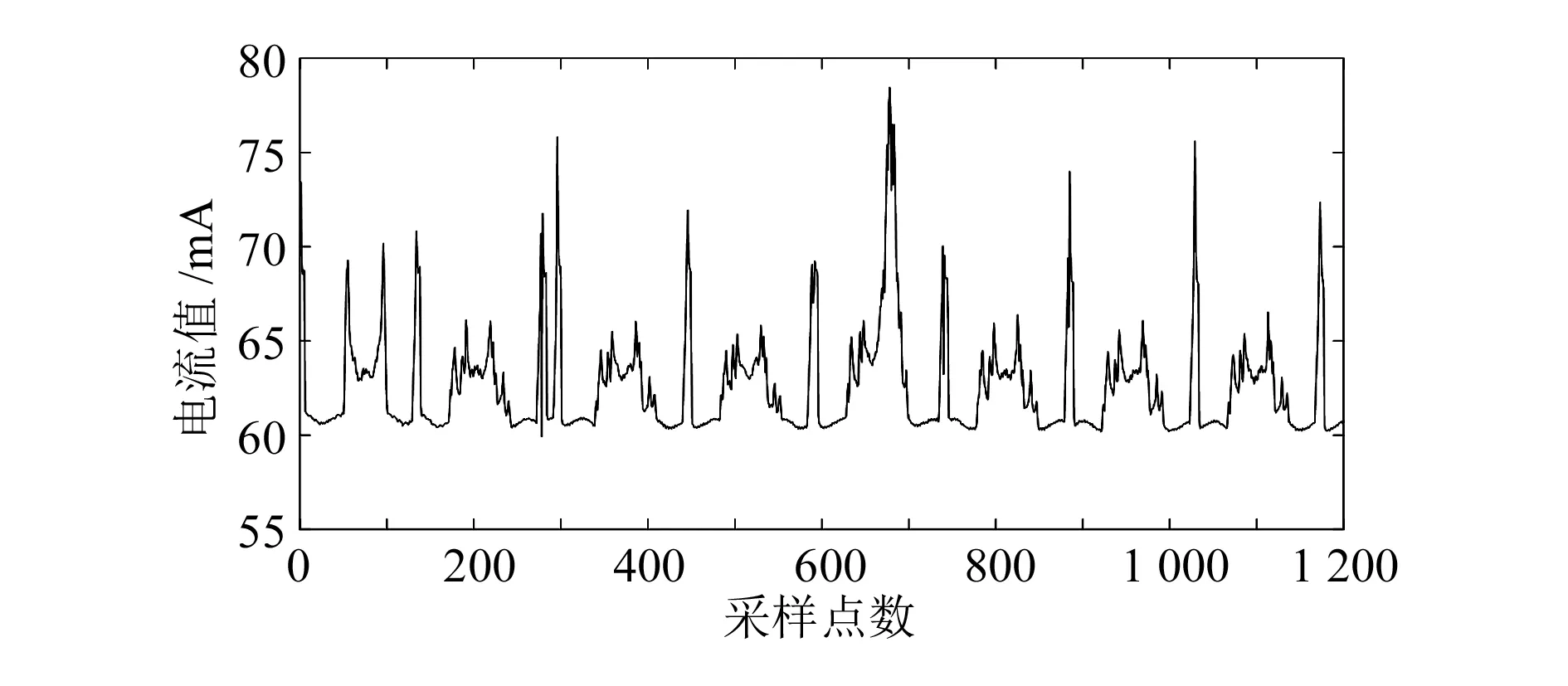
图2 1#主锯电机电流值

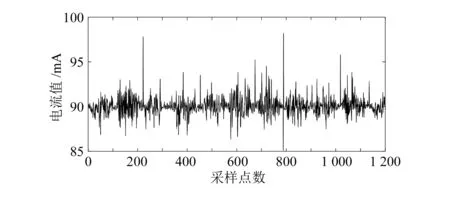
图3 2#主锯电机电流值

2 BAS-BP神经网络模型建立

使用BAS对BP神经网络的权值和阈值进行优化[8]，并将其结果应用到已经设定的神经网络中，构造出最终的BAS-BP神经网络模型。构建模型的具体步骤如下：

1)对天牛须随机搜索向量做归一化处理[9]：

(1)

式中：b为天牛须朝向随机向量；rands()为随机函数；k为空间维度。若BP神经网络模型为m-h-1时，则k=m×h+h×1+h+1，其中m为输入层神经元个数，h为隐含层神经元个数。

2)创建天牛左右须空间坐标：

(2)

式中：xrt,xlt分别为天牛右须、左须第t次迭代时的位置坐标；xt为天牛第t次迭代时的质心坐标；dt为天牛第t次迭代时两须之间的距离。

3)根据适应度函数f()判断两须的气味强度，即由f()来判断天牛右须f(xr)和天牛左须f(xl)的气味强度，判断天牛位置移动方向：

xt+1=xt-δt×b×sign(f(xrt)-f(xlt))

(3)

式中：δt为第t次迭代时的步长因子；f(xlt)，f(xrt)分别为天牛第t次迭代时左右两须的适应度函数值。

4)由于可用步长因子δt来控制天牛的区域搜索能力，因此选取的初始步长尽可能大，使之足以覆盖当前的搜索区域而不至于陷入局部极小，则δt随时间的变化函数式：

δt+1=δt×eta(t=0,1,2,…,n)

(4)

式中：eta为步长衰减因子，取值范围为[0,1]，这里取0.8。

5)以测试样本数据的均方根误差MSE作为适应度评价函数：

(5)

式中：fitness为适应度评价函数值；S为训练集样本数；ymi为第i个样本的模型输出值；yi为第i个样本的实际值。MSE的值越小则模型精度越高。

6)随机给定天牛的初始位置，计算其适应度函数值，并保存在bestX,bestY中。其中，bestX为最佳的天牛初始位置，bestY为天牛初始位置的最佳适应度函数值。

7)根据式(2)更新天牛两须的位置坐标，分别求左右两须的适应度函数值f(xl)和f(xr)，将这两个值进行比较后根据式(3)更新天牛移动位置，并计算在当前位置下的适应度函数值，如果适应度函数值优于bestY，更新bestX和bestY。

8)当适应度函数值达到设定精度或迭代达到最大次数，算法运行结束。将此时bestX中的解作为最优权值和阈值代入BP神经网络中，最终形成BAS-BP神经网络模型。

综上所述，经过BAS优化后的BP神经网络模型流程如图4所示。

3 BAS-BP神经网络模型对电流预测

本文选取两台主锯的108组电流数据作为总样本。其中，前89组样本数据作为训练样本，输入到新模型中进行训练，剩余的19组作为测试样本对新模型进行验证。以MATLAB 2015b为平台，使用自带的神经网络工具箱[10]。经过反复验证计算，最终确定初始步长δ=10,迭代次数n=100，空间维度k=51。BAS-BP神经网络模型采用常见的三层神经网络结构，输入层神经元个数为3，输出层神经元个数为1，根据经验公式计算隐含层神经元个数h可得h=10。本文建立了3-10-1的三层神经网络结构模型。

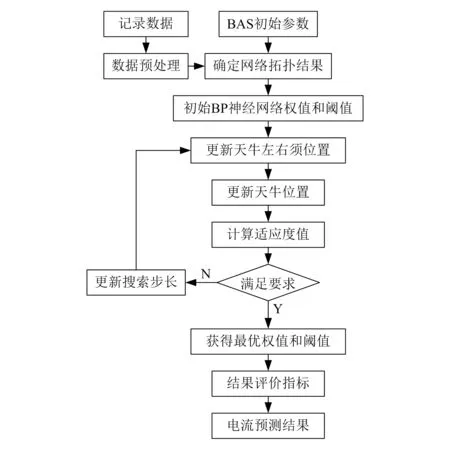
图4 BAS优化BP神经网络模型流程

图5和图6分别为BAS算法寻优的迭代结果。由图可知，1#锯大约经过16代接近收敛，2#锯大约25代就接近收敛，此时结果接近最佳适应度，即最优解分别为0.011 50和0.016 15。图7和图8分别为两台主锯电流优化前后的预测值与实际值对比，可以看出BP与BAS-BP的预测值变化趋势相同，而BAS-BP的预测值更加接近实际值，且精确度明显更高。

图5 1#锯迭代结果

图6 2#锯迭代结果

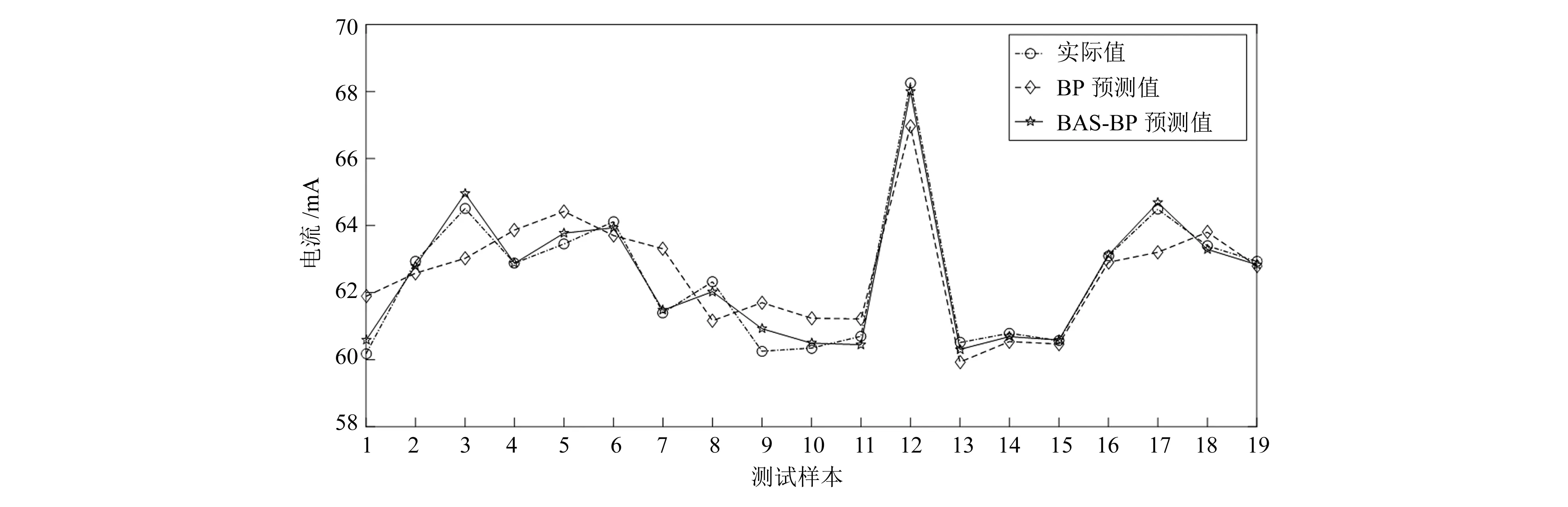
图7 1#锯优化前后预测值与实际值对比

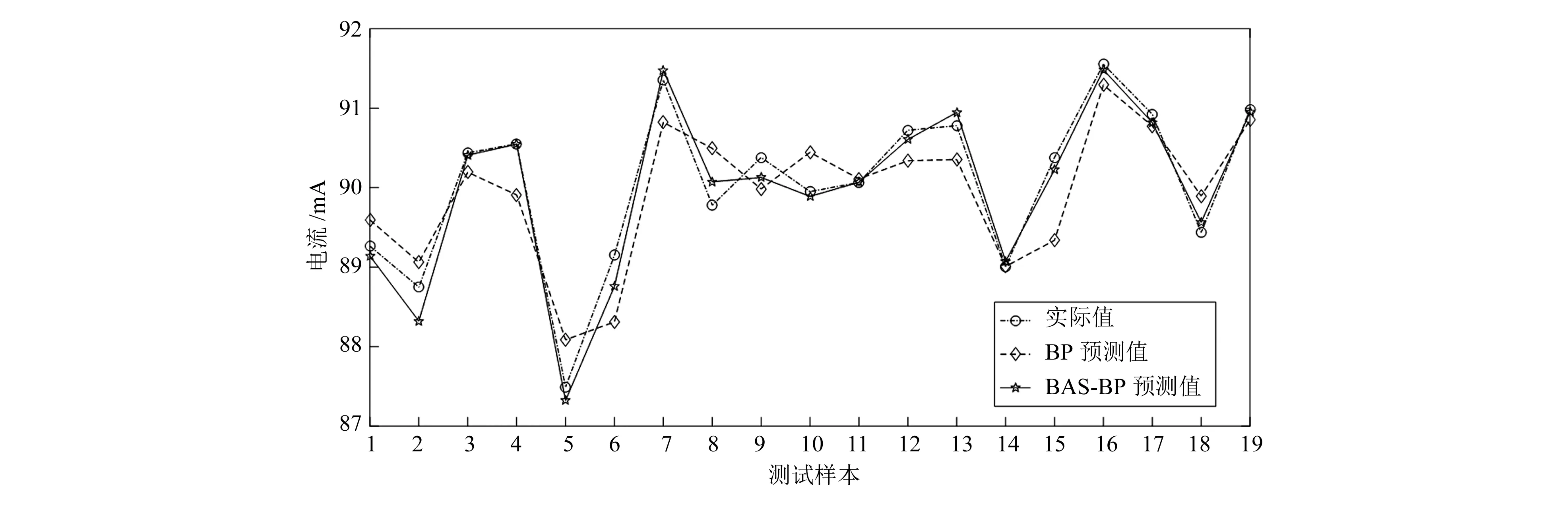
图8 2#锯优化前后预测值与实际值对比

为了验证BAS对BP算法的优化效果，将预测评估指标均方误差(MSE)、均方根误差(RMSE)、平均绝对误差(MAPE)进行对比。由表1可知，BAS-BP神经网络模型的预测评估指标相比BP神经网络分别降低了32%、28%和15%。由表2可知，BAS-BP神经网络模型的预测评估指标相比BP神经网络分别降低了12%、22%和17%。以上结果表明，BAS优化后的BP神经网络在收敛速度、精确度方面均有显著提高。综上所述，采用BAS-BP神经网络模型对电流的预测效果更好。

表1 1#主锯两种算法的评估效果

表2 2#主锯两种算法的评估效果

4 结束语

本文以两台主锯的异步电机电流数据为基础，将BAS与BP神经网络结合建立了BAS-BP神经网络模型，对异步电机电流进行预测。通过BAS优化后的初始权值和阈值明显优于传统BP神经网络的初始权值和阈值，加快了样本训练速度和收敛速度，且预测精确度显著提高，同时避免BP神经网络易陷入局部最优的缺陷。本文运用该模型对锯切电流变化趋势进行了预测评估，为异步电机的电流预测评估提供了一种新的方法。