基于有限元分析的高速精密数控机床床鞍机构设计

朱 军

(宁夏工商职业技术学院，宁夏 银川 750021)

与普通机床相比，高速精密数控机床的切削速度、加工精度更高，其机械部件需具备高强度、高刚度及轻质结构等特点，以确保可承受较大的外力作用[1-2]。由此可知，提高机床零部件性能及合理的设计方案，是提高机床整体性能的关键。床鞍虽然只是数控机床的重要零部件之一[3]，但床鞍的静动态性能对数控机床整体性能却有着决定性作用。国内外已有学者对机床的静动态性能开展研究，并获取丰厚的研究成果，但以往的研究过分重视研究对象的具体优化，忽略了机床零部件对机床整体性能的影响[4]。将研究对象的优化目标函数、约束条件、设计变量确立的拓扑优化方法备受重视，本文将采用这种方法，并基于有限元分析，建立优化模型，以此获取研究对象的最佳设计方案[5]。当前床鞍机构以类比设计与经验设计为主，由于此类方法缺少有效合理的设计依据，且性能低、质量过大,无法满足当下高速精密机床的发展趋势，因此寻求提高床鞍机构性能、减小质量的优化设计方法尤为重要[6-9]。

1 方法研究

1.1 床鞍有限元分析

本文采用有限元软件对高速精密数控机床床鞍建模，为了能够快速、准确地分析床鞍有限元模型，有限元模型质量还需要提高。为保证分析的准确性并提高运行速度，在对数控机床床鞍建模时，应调和床鞍现实工况与理论研究速率两者间的关联,并在采用有限元分析床鞍机构后，依照分析结论提出有效的改善方法。

1.2 床鞍有限元建模

由于食品加工材料较为软糯，需要保证加工后的食品具有极高的完整度，以及为便于机床的移动及食品的加工，对床鞍质量和静刚度有极高的要求，因此食品加工数控机床对床鞍变形量及特定频率有严格要求。某食品加工厂的数控机床在Pro/E软件中建立的三维模型[10]如图1所示。为了使数控机床达到食品加工的要求，需要适度简化床鞍的初始模型，即按照极限位置正方向Z调整数控机床的尾架与床鞍，按照极限位置负方向X调整刀塔与滑体，如此床鞍就能被调整到最差的受力位置，以方便对床鞍机构进行观测。

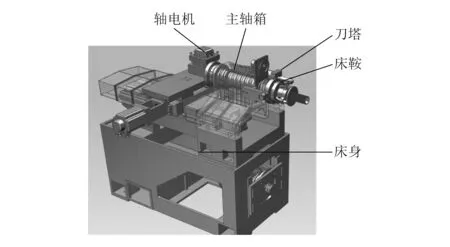
图1 数控机床三维模型

为了更好地对床鞍机构内部进行观测，在HyperMesh中对床鞍基本结构实行拓扑优化。在保证不改变床鞍外廓形态的情况下填充床鞍初始机构内的空隙，以便在合理划分拓扑机构形态材料的情况下获取，且拓扑优化的初始机构便是经过处理的机构。如图2所示。在HyperMesh中植入经过处理的床鞍三维实际模型，采用六面体单元网格划分床鞍模型。

图2 拓扑优化床鞍初始结构

1.3 床鞍边界条件建立

对床鞍增加制约与载荷，需在完成网格划分的前提下，对滑体采用静力分析获取重力以外的其他载荷，通过现实工况选取适宜的制约方法以增加制约。对床鞍制约与载荷状况进行详尽分析，结果如图3所示。

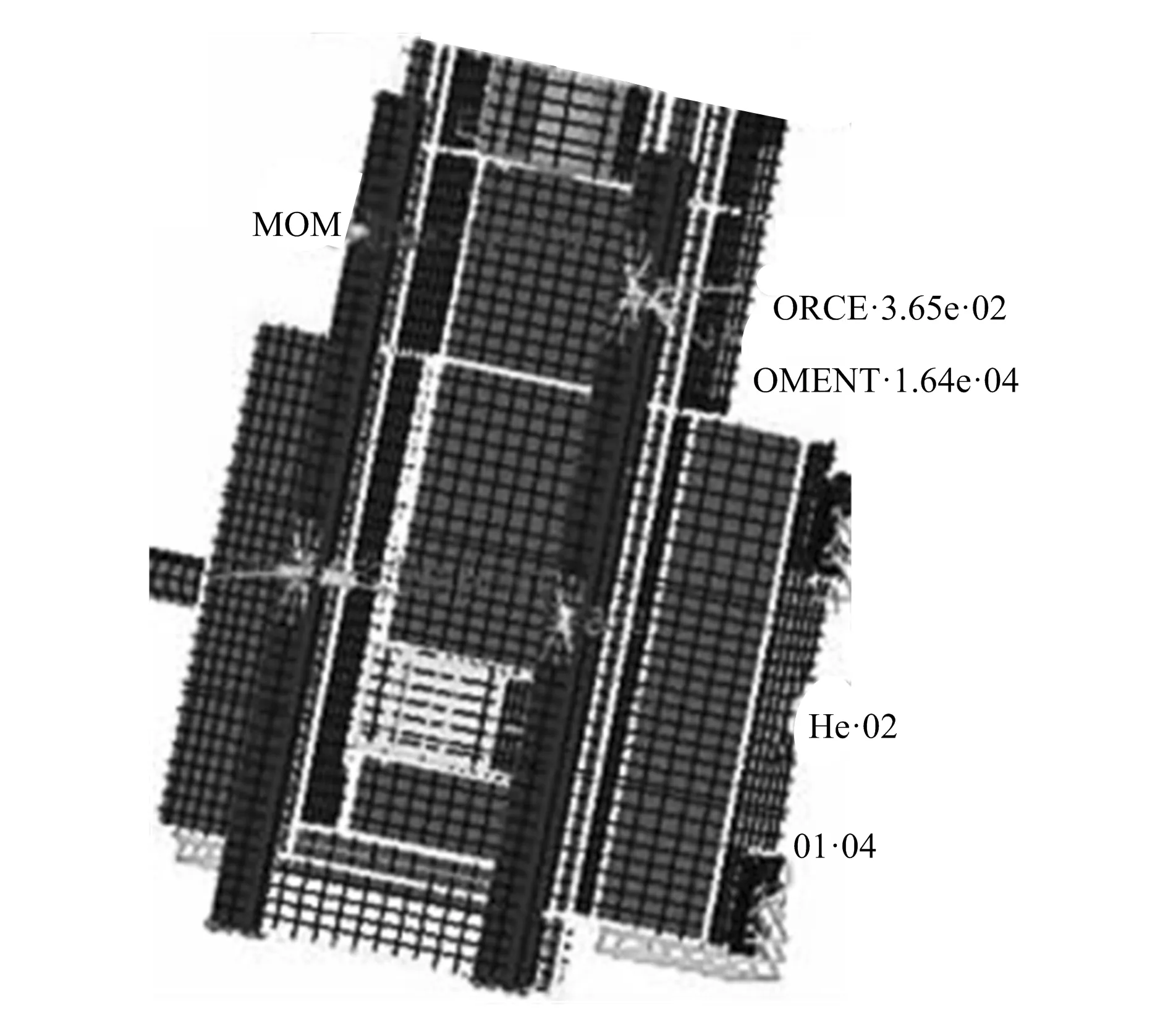
图3 床鞍载荷与约束

1.4 床鞍有限元分析结果

通过静态分析和模态分析可知在极限工作环境下床鞍的变形情况以及床鞍每阶固定频率，以此可以检测床鞍和数控机床激振频率能否产生共振。此外通过对床鞍有限元的分析还可以检测出床鞍机构的薄弱环节，以便为之后的拓扑优化设计床鞍机构奠定基础。

由分析可知，床鞍左侧的导轨下方易出现床鞍整体形态变化，且形变大小接近0.022 mm。床鞍的整体1阶模态是172.3 Hz，通过n=50f的转速频率关系，可求出1阶特定频率的相应转速大约为10 383 r/min，而本文数控机床的主轴转速区间是40～2 200 r/min，显然比1阶特定频率的转速低，因此床鞍与激振频率间不会出现共振情况，证明床鞍动态性能较好。

在采用拓扑优化设计床鞍期间，需竭力维系1阶的较高特定频率，降低形态变化并减轻床鞍的质量。

1.5 基于变密度法的床鞍机构设计

1.5.1拓扑优化建立机构模型

变密度法的基本原理即为假定一种实际中不可能出现的材料单元，并且在区间[0，1]中材料密度发生改变[11]，床鞍机构设计的拓扑优化理论便是依据此方法形成的。密度和弹性模量两者间的假设函数关系通过设定一个经验公式表示，该公式将各单元的密度作为设计变量。本文设置工、#、米、X 4个单元，通过对这4个单元的研究,将拓扑优化问题转化为单元材料的最优分布问题。

分析动态与静态情况下的床鞍特性结果可知，目标函数和约束条件分别为床鞍质量的减轻和床鞍前三阶特定频率、床鞍极限形态变化，采用变密度法对床鞍拓扑优化的数学模型如下：

findμ(X)={μ1,μ2,…,μm}y∈Ω

(1)

minO=μP

(2)

(3)

式中：μ为设计变量；m为优化设计变量数目；μm和μj分别为第m个和第j个需优化的设计变量；O为目标函数；X为床鞍密度函数；Ω为床鞍质量函数；P为单元面积；约束函数af(X)、bg(X)、ch(X)为床鞍前三阶特定频率；di(X)为床鞍极限形态变化函数；e为床鞍的整体固有频率。基于以上算法，可得出式(4)：

(4)

式中：Me为机构初始实心单元弹性模量；Ne和kej分别为初始刚度阵和初始质量阵；M，N，k分别为单元等效弹性模量、刚度阵、质量阵；g1为惩罚权因子。

单元相对密度与材料属性间的相对性关系，可通过变密度法以持续变量的密度函数形式表达。设计变量是各单元的相对密度，与材料属性形成指数关系。对(0，1)间的设计变量中间密度值的惩罚采用变密度法的惩罚因子实现[12]，便于消除中间密度材料，可令拓扑优化模型在持续变量情况下与传统0-1拓扑优化模型在离散变量情况下更接近。当惩罚作用越好时g1越大，通常取g1=2，可以避免g1过大造成系统矩阵奇异而难以保证获得准确的拓扑结果现象。

1.5.2拓扑优化设计结果

先确定床鞍设计的优化及非优化区域，并研究机床各零部件间的装配关系，从而确定导轨的接触面。非优化区域是4个滑块的安装区间与轴承座[13]，需要对其实行拓扑优化。

对床鞍的拓扑优化设计需在床鞍有限元模型建立之后进行，设计变量是优化区域中各单元的相对密度，目标函数是床鞍的刚度。床鞍一阶特定频率在优化后要比约束条件(300 Hz)高，本文将在该约束条件下得出拓扑优化的结果。拓扑优化结果中的某个设计变量是wi，其对结构材料的去除量有抉择作用，多次调节并选定系数wi为50%，可更好地将床鞍材料留存下来。保持床鞍形态变化量最高便于获得最好的结构材料分布[14]，图4所示为床鞍拓扑优化结果。

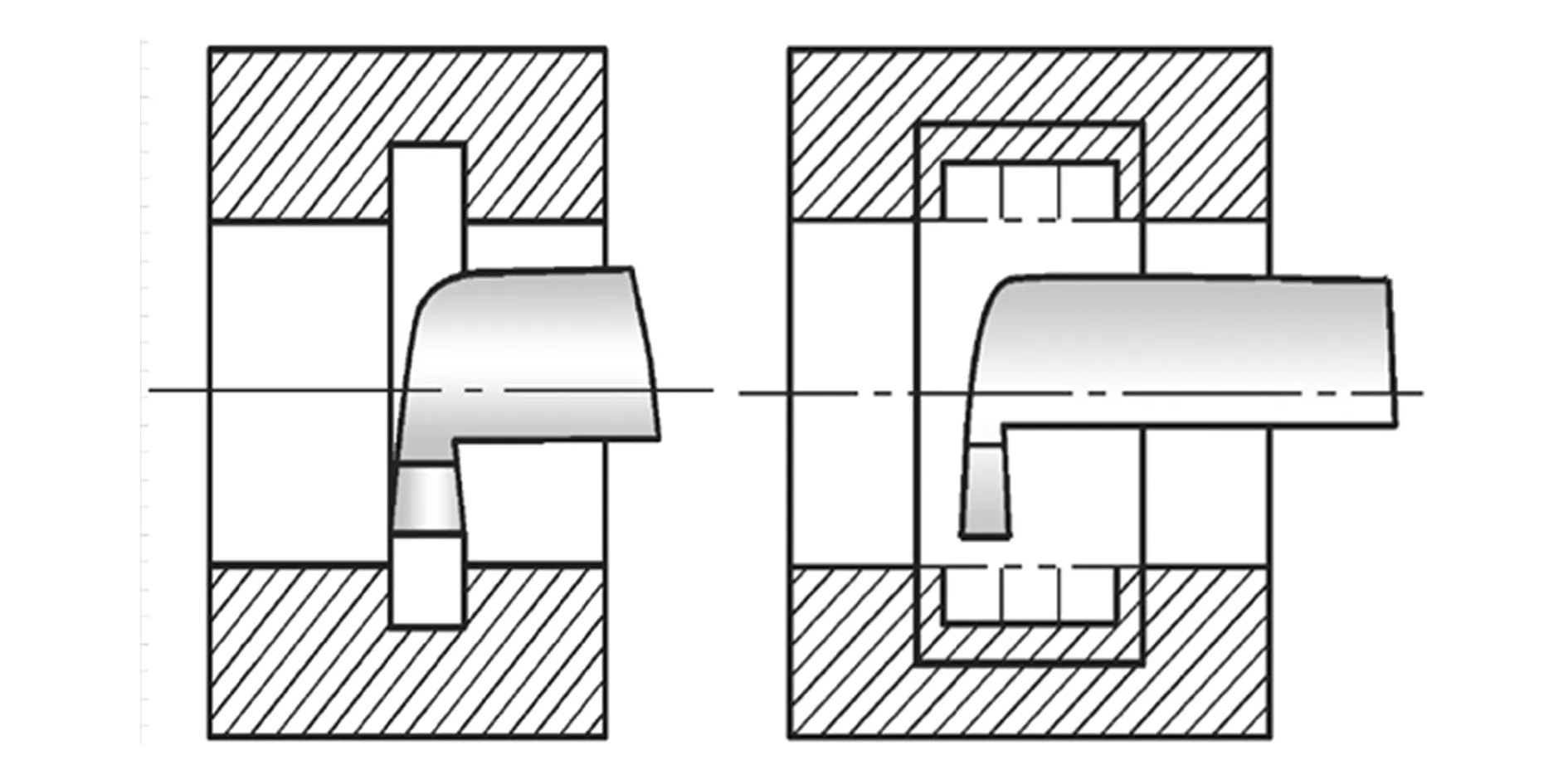
图4 床鞍拓扑优化结果

1.5.3床鞍机构新方案设计

分析拓扑结果可知，拓扑模型中结构材料分布的位置接近导轨，且加强筋在中间增多布设，但要撤换床鞍底板的多数材料如铁素体等。由力学性能方面的分析可知，导轨横向力及导轨对位移制约的弯矩作用均被上方增多的与丝杠轴承座相接的材料抵消[15]，床鞍的极限位移可通过此结构减少。机床主要基础铸件(包括床身、立柱、主轴箱等)采用的高强度灰口铸铁材料,具有极佳的机械稳定性和耐热性,在机床进行重型强力或间歇切削时,具有优异的减震性，能大幅度提高床鞍抗扭、抗弯性能及静动力。

依据分析结果规则化设计床鞍，将床鞍上方的中间位置材料替换，保留下方的4个滑块及轴承座位置，采用加强筋将中间位置相连，并向上下两侧分布材料，以便提高床鞍的抗扭与抗弯刚度。图5所示为床鞍的新方案初步设计结果。

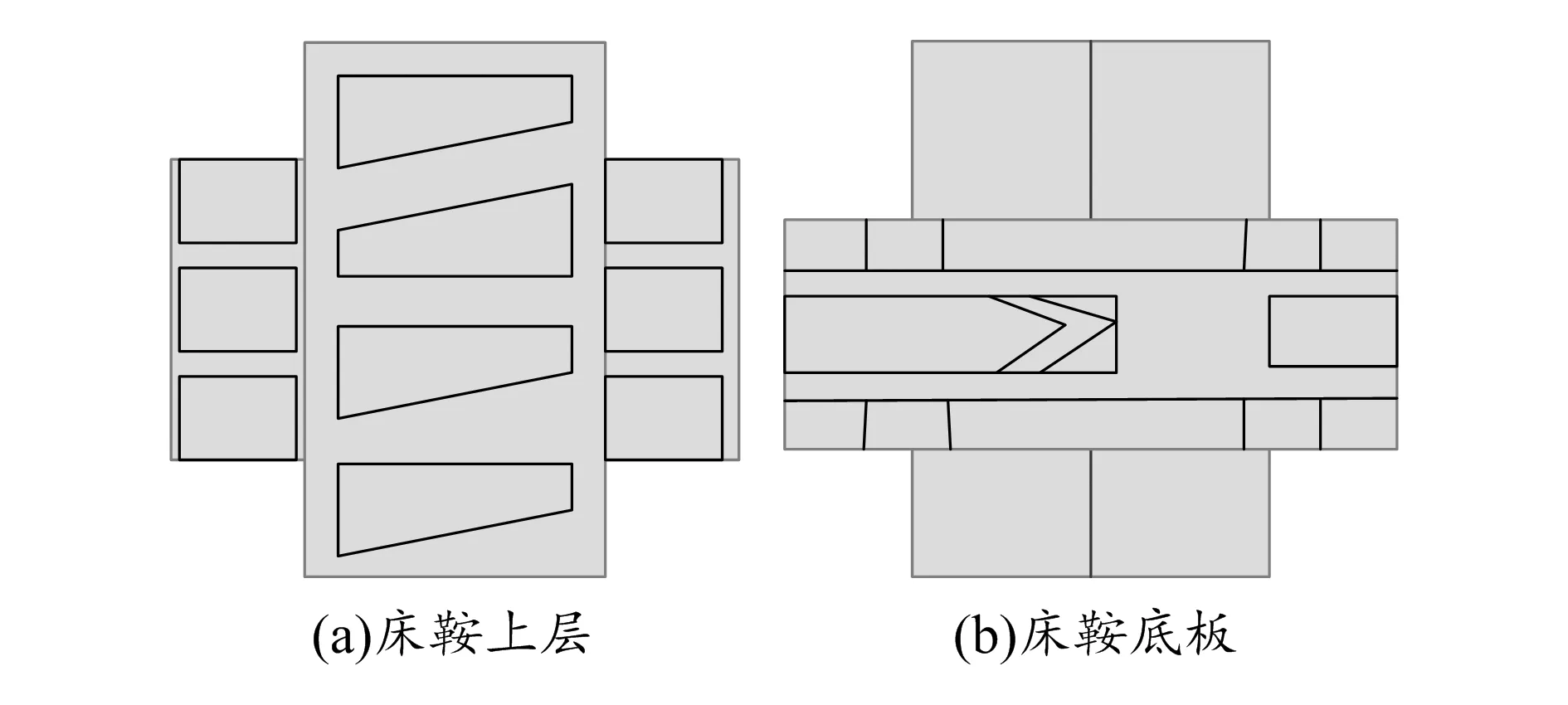
图5 床鞍初步结构设计

在上述床鞍初步结构设计的基础上，基于结构化单元改进床鞍结构。高速精密数控机床的重要支撑件便是床鞍，为使机床震荡减轻、静动刚度提升，设计时需增加加强筋于静刚度弱的位置。

本文通过变密度法拓扑优化将床鞍结构中对床鞍静动态特征无过多作用的单元除掉，以获取床鞍的优化结构。需要注意的是，为避免床鞍静刚度减弱，不可将床鞍材料统一替换，应先在空腔中增加适量的筋板以保证其刚度性能不被减弱。

2 实验分析

2.1 各类单元床鞍的静动态性能

工装单元的单元形式与类型具有多样性，而单元的结构特点却具有相近性。将支撑件结构单元划分为4类，分别为壁板类单元、加强筋类单元、工艺类单元与箱体类单元。其中将壁板类结构单元用符号表示，分别为工、#、米、X、V、N等，本文以工、#、米、X4种单元类型为例，分析用本文方法设计的床鞍机构的静动态性能。

利用有限元分析床鞍的4类单元，以获得床鞍静动态的性能对比结果(表1)。

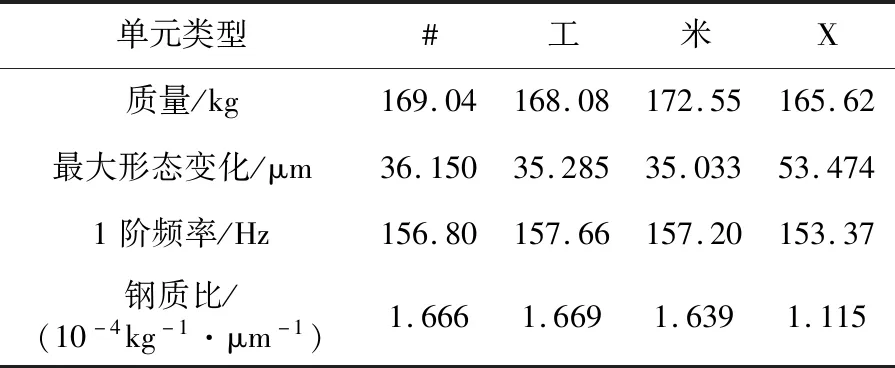
表1 各类单元床鞍的静动态性能对比

通过表1可知，用本文方法设计的床鞍机构一阶特定频率在各类单元中均可达标。4类单元的床鞍静刚度最优的为工型单元，#、米、X次之，工型单元的静刚度更优是因为筋板位置布置最恰当；而在X型单元过大的设计区域中采用单个空腔面积，虽减少了材料的耗损，却降低了刚度。

2.2 优化求解

由于X型单元刚度降低，因此将其排除，通过优化工、#、米3个单元待选值，得出每个单元值对应的输出结果，见表2。

表2 优化结果对应1阶特定频率与质量

分析表2可知，3组的质量接近，无明显差距，而工型待选组的1阶特定频率却明显高于其他两组。综合以上两点可知，工型待选组为最佳的优化结果。

2.3 床鞍新方案性能评估

对4类单元工、#、米、X分别设置对应的A、B、C、D 4种方案，为了获取床鞍机构的最佳形式，在同等载荷条件下对4种方案进行静力分析，如图6所示。

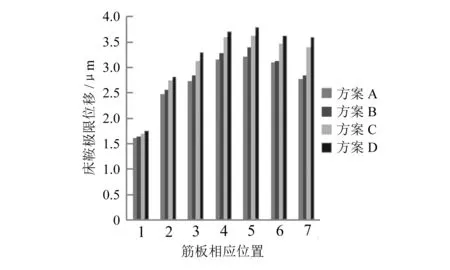
图6 不同筋板设置方案床鞍位移

通过图6可知，当载荷条件相等时，床鞍极限位移量最小的是方案A，其次是方案B和C，而方案D位移量最大，所以选取工型单元为用本文所提方法设计的床鞍最优结构形式。

将选取的工型单元作为新床鞍结构形式，与原床鞍结构做对比，结果见表3。

表3 床鞍新结构和原结构对比结果

通过表3可知，利用本文所提方法设计的新床鞍质量减小近14%，最大变形量降低9%，大幅度提高了床鞍的静刚度；床鞍的6阶特定频率分别提升了10.0%、6.0%、6.8%、4.7%、9.0%、10.8%，由此可以证明床鞍的抗干扰能力与可靠性得到提高。基于以上分析可知，本文方法在保证床鞍刚度的基础上减少了用料，为床鞍的机构设计和后续生产提供了依据。

2.4 约束与自由状态下特定频率对比

对新结构与原结构分别在约束状态下、自由状态下的6阶特定频率作对比，如图7所示。

通过图7可以看出，在约束状态与自由状态下，本文所提方法设计的新结构的6阶特定频率均高于原结构，说明使用本文所提方法设计的高速精密数控机床床鞍新结构的频率更优，稳定性与抗干扰能力更强。

3 结束语

本文给出的基于有限元分析的高速精密数控机床床鞍机构设计方案具有较高的实用性，在一定程度上能够加强床鞍机构静刚度，使其不易产生位移及变形，具有更高的稳定性，为提高高速精密数控机床的整体性能提供了一定的技术支持。但是，目前的研究工作仅通过较为简单的实例来验证实现方案的可行性，要真正体现其价值，还需要通过后续大量实践产生的数据对方案进行细化，以求进一步完善高速精密数控机床床鞍机构设计方案。

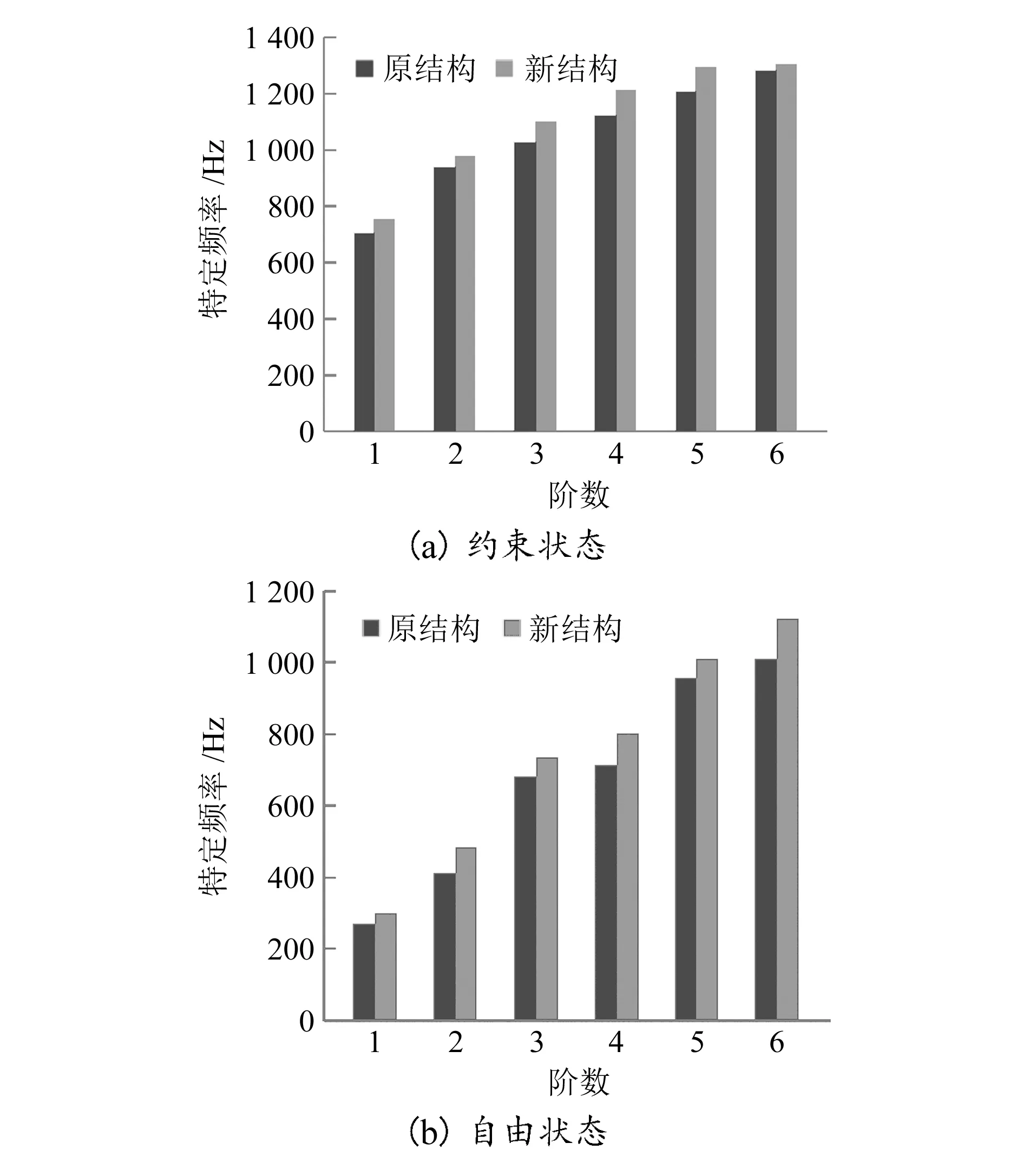
图7 两种状态下的6阶特定频率