多维关联因素筛选条件下的堆积层滑坡体积预测研究

黄 鑫， 权朝斌， 王 辉， 龙海忠， 何钟强

（青海省水文地质及地热地质重点实验室（青海省水文地质工程地质环境地质调查院），西宁 810008）

三峡库区地形起伏较大，使得区内滑坡灾害较为发育，且受长江航道限制，滑坡规模是其威胁性的直观体现，即其规模越大，影响范围也越大，对长江航运的威胁也就越大［1-4］. 因此，为保证长江航道的正常运营，有必要深入开展滑坡规模研究，且区内堆积层滑坡所占比例达80%，进而以堆积层滑坡为研究对象具有意义. 受区域地质条件影响，滑坡成因较多，已有学者开展了该方面研究. 陈亮青等［5］、易庆林等［6］通过影响因素筛选，构建出了滑坡变形预测模型，有效指导了后期灾害防治，但上述研究均是针对变形影响因素的筛选研究，未涉及堆积层滑坡规模的影响因素分析，进而仍待进一步拓展研究.

同时，在滑坡规模研究中，也有相关学者开展了相应研究. 张群等［7］利用BP神经网络构建了滑坡体积预测模型，具有较好的准确性；黄志全等［8］则以数量化理论和BP神经网络为基础，构建了滑坡体积规模分析模型，不仅有效分析了各因素对滑坡体积的影响程度，还实现了滑坡体积预测. 上述研究虽取得了相应成果，但均未涉及三峡库区堆积层滑坡研究，为切实保证库区航运及区内居民的生命财产安全，仍有必要进一步开展三峡库区堆积层滑坡的影响因素分析及规模研究. 因此，该文以31个三峡库区堆积层滑坡为工程背景，通过参数统计，先分析各体积影响因素的分布规律，再开展其与滑坡体积间的相关性评价，最后在前述相关性评价结果基础上，利用混沌理论、粒子群算法及极限学习机等方法构建滑坡体积预测模型，以实现滑坡体积预测研究.

1 分析方法与模型构建

该文分析过程主要包含两个阶段：第一阶段是在滑坡体积影响因素统计的基础上，开展各因数的分布规律研究，并利用相关系数评价各因素与滑坡体积间的相关性程度，以筛选出滑坡体积的重要影响因素；第二阶段是基于前一阶段成果，利用混沌优化极限学习机构建滑坡体积预测模型，实现滑坡体积预测研究.结合上述思路，将该文涉及方法的基本原理分述如下.

1.1 影响因素的相关性分析

滑坡体积的规模成因相对较多，且不同成因因素对滑坡体积的影响程度存在一定差异，进而有必要合理评价不同因素与滑坡体积间的相关性，即若某因素与滑坡体积的相关性较高，说明其对滑坡体积的影响较大；反之，说明其对滑坡体积的影响较小［9］. 同时，相关系数法是一种统计方法，具有可信度高、易于操作等优点，适用于滑坡体积与其影响因素的相关性评价. 在相关系数的求解过程中，若影响因素为xi，滑坡体积为yi，则两者的相关系数可按下式计算：

式中：x′、y′为平均值.

可利用上式计算得到的r值判断影响因素与滑坡体积间的相关性，判据为：当r＞0时，说明评价因素对滑坡体积呈正相关，即该因素与滑坡体积的变化趋势相同；反之，说明评价因素对滑坡体积呈负相关，即该因素与滑坡体积的变化趋势相反. 同时，根据r值的绝对值大小可判断影响因素与滑坡体积间的相关性程度，具体划分标准如表1所示.

表1 相关性程度划分标准Tab.1 Classification standard of correlation degree

1.2 体积预测模型的构建

鉴于极限学习机（Extreme Learning Machine，ELM）的预测效果，以其为基础构建滑坡体积预测模型；且利用前述相关性评价筛选出的滑坡体积重要影响因素作为滑坡体积预测模型的输入层，保证了输入层信息的有效性，促使该文体积预测模型具多维关联特征［10-16］. 同时，ELM模型是一种新型神经网络模型，具三层拓扑结构，分别为输入层、隐含层和输出层，其训练过程为：

若样本表示为(xi，ti，i=1，2，…，N)，则ELM模型的训练过程可表示为：

式中：yj为预测值；xi为输入信息；L为隐层节点数；g(x)为激励函数；βi，wi为连接权值；bi为阈值.

由于ELM模型具有神经网络特征，其训练过程可实现零误差逼近，即：

式中：tj为实测值；N为训练样本数.

根据ELM模型的训练过程，其模型参数的选取过程存在一定不足，如：①激励函数种类较多，无统一选取标准；②隐层节点数由使用者设定，难以保证其最优性；③节点间的连接权值和阈值具有随机性.

上述问题均很大程度上影响预测精度，有必要进行优化处理，将三者具体优化处理方法详述如下.

1）激励函数的优化. ELM模型的核函数种类较多，常用的有Hardlim型、Sigmiod型、Sine型和RBF型，由于不同核函数的预测效果存在一定差异，为保证核函数的最优性，该文利用试错法确定最优核函数，即对四种核函数的去噪效果均进行计算，所得预测效果最佳者即为该文ELM模型的核函数.

2）隐层节点数的优化. ELM模型也属神经网络模型，其隐层节点数的经验公式为：

式中：m、n为输入、输出层节点数；a为调节常数（一般取10）.

上式虽能确定隐层节点数，但无法保证隐层节点数的最优性，进而该文提出以上述公式计算得到的初步隐层节点数为中心，对其进行扩展取值，并试算所有隐层节点取值的预测效果，以确定出最优隐层节点数.

3）连接权值和阈值的优化. 粒子群算法（Particle Swarm Optimization，PSO）是一种全局优化方法，已被广泛应用，但传统PSO算法是采用线性递减策略来实现惯性权值调整，难以有效平衡局部与全局的搜索能力，进而该文采用IPSO 算法来优化ELM 模型的连接权值和阈值，该方法是采用非线性动态方法来实现惯性权值调整，能有效兼顾全局与局部的搜索能力，避免出现优化早熟或波动振荡等现象［17-20］. 结合IPSO算法的基本原理，将其对ELM 模型连接权值和阈值的优化过程详述如下：①参数初始化. 将粒子群规模设置为450，粒子维数为2，分别代表连接权值和阈值，最大迭代次数为500次，其他参数随机设置. ②迭代寻优. 将预测误差作为适宜度值，并对比粒子与全局的适宜度值，当前者更优时，则用粒子适宜度值替换全局适宜度值；反之，改变粒子的位置及速度，继续迭代寻优. ③参数输出. 当达到最大迭代次数或期望误差时，结束寻优，将全局适宜度值对应的连接权值和阈值输出，将其作为ELM模型的对应参数，进而实现连接权值和阈值的参数寻优.

根据上述优化方法，将具体优化过程设定如下：①先利用传统经验公式初步确定隐层节点数，再利用试错法确定最优核函数；②扩展隐层节点数的取值区间，并试算不同隐层节点数的预测效果，以确定最优隐层节点数；③利用IPSO算法实现连接权值和阈值寻优，以完全实现ELM模型的参数寻优.

上述研究虽有效保证了ELM模型的参数最优性，但值得指出的是，受误差因素影响，优化ELM模型难以完全刻画滑坡体积预测，即优化ELM模型的预测结果存在一定误差，且该类误差具有一定的混沌特征，为进一步提高预测精度，该文再利用混沌理论实现ELM模型预测结果的误差弱化.

将混沌理论的误差弱化过程设定为：①先利用Lyapunov 指数法判断待弱化误差的混沌特性，即当最大Lyapunov指数大于零时，得出预测误差具有混沌特性，适用于混沌理论进行误差弱化处理；②以嵌入维数和延迟时间为基础，对待弱化误差进行相空间重构，且嵌入维数的确定方法为自相关法，延迟时间的确定方法为互信息法；③在相空间重构基础上，反求预测误差的预测值，并将其预测结果与前述优化ELM模型预测结果叠加，以实现滑坡体积的最终预测.

2 实例分析

2.1 工程概况

三峡工程位于湖北宜昌，其库区范围较大，沿长江干流纵向长度约685.2 km；同时，区内地貌单元变化显著，主要包括丘陵地貌和中低山地貌，且地形起伏较大，地形分类主要有三类，即以重庆库区为中心的山地、丘陵地形；以河谷洼地、阶地为中心的平缓地形；以库区斜坡为中心的斜坡地形.

根据区域地质资料，区内地层发育较为齐全，主要发育有志留系、二叠系、三叠系及侏罗系基岩，且第四系堆积层也较为发育，为区内滑坡灾害提供了丰富的物源. 同时，三峡库区范围内的构造较为强烈，一级构造单元主要为扬子淮地构造，二级构造单元主要为扬子四川台坳、台褶皱带、大巴山坳褶带及江汉-洞庭坳陷，受上述构造单元影响，使得区内基岩节理裂隙及褶皱构造发育，利于地下水赋存，不利于斜坡稳定.

受三峡工程蓄水影响，区内水文条件的季节性变化差异较大，将各类地下水特征分述如下.

1）地表水：由于库区范围较广，其地表水资源较为丰富，主要分布于长江支流，具不对称分布，受气候及库水位升降影响较大.

2）地下水：由于区内基岩节理裂隙较为发育，且第四系地层分布较厚，使得区内地下水也较为丰富，主要接受降雨及地表水补给，受库水位升降影响，水力联系也较为复杂.

同时，受库区移民搬迁等工程影响，区内人类工程活动较为强烈，主要工程活动包括水库建设、移民城镇建设、矿山开采及毁林开荒等活动.

受区域地质条件影响，三峡库区历来发育有大量滑坡灾害，加之水库蓄水，进一步诱发了大量滑坡，其中，堆积层滑坡较为发育，进而将其作为该文的研究对象. 同时，结合工程实际，将库区堆积层滑坡的体积影响因素分析如下.

1）坡体空间位置因素：滑坡所处空间位置会影响岩土体所处的环境条件，进而影响滑坡稳定性，其主要评价因素包括分布高程及高差等.

（4）积极指导，政策支持。秸秆发电项目工程是极典型的系统工程，国家须给予一定的支持并制定相关的指导政策。并强化立法，加强政策体系的建立、创新和推广。针对秸秆回收困难所存在的问题，政府需要加大秸秆田间禁烧工作力度，奖罚分明。建议政府出台奖励政策，用于补贴和奖励秸秆收购企业。另外政府还应不断改善投、融资环境，建立通畅的投、融资渠道。

2）滑坡特征因素：滑坡固有的特征因素与其规模直接相关性，主要包括滑体厚度、坡体结构、剖面形态及物质组成等因素.

基于上述分析，对三峡库区范围内31个堆积层滑坡进行了基础参数统计，结果如表2所示.

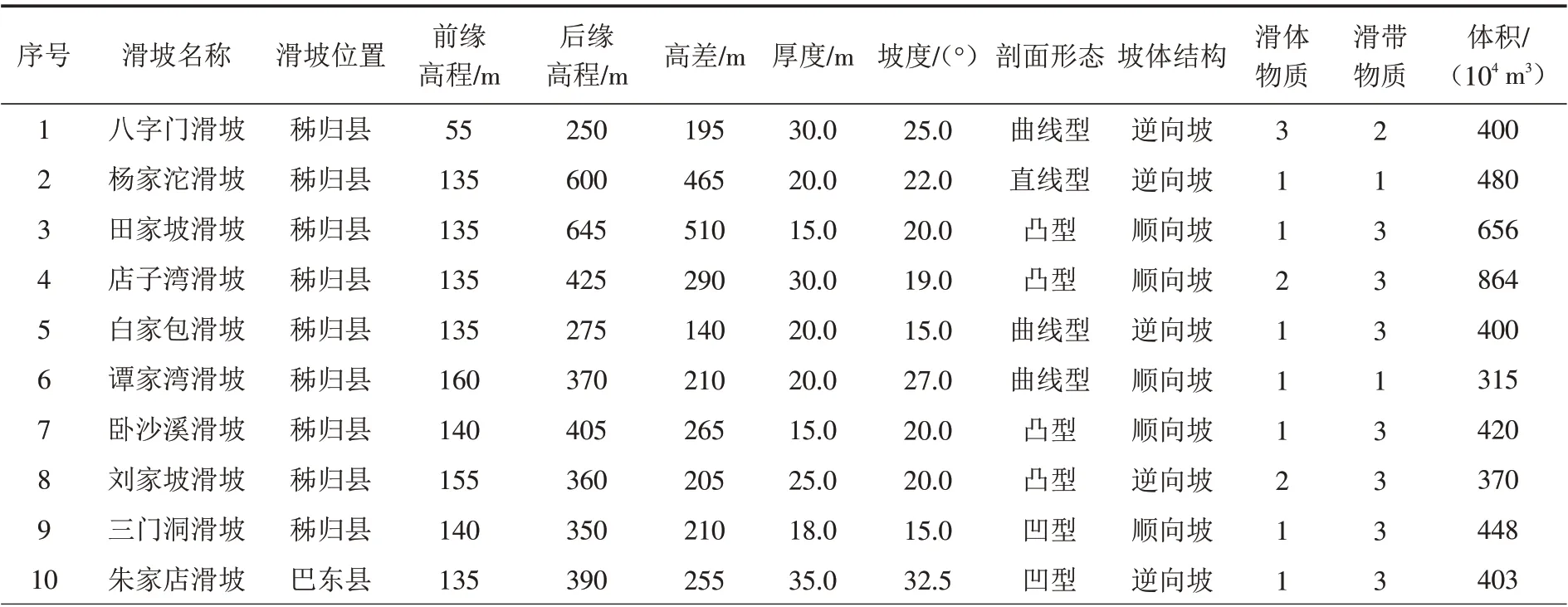
表2 三峡库区堆积层滑坡基本参数统计Tab.2 Statistics of basic parameters of accumulation landslide in Three Gorges Reservoir Area

续表

2.2 影响因素分布特征分析

该节重点分析三峡库区滑坡体积影响因素的分布规律，且在分析过程中，滑坡分布高程、高差、厚度及坡度均是实测值，可利用变异系数对其波动性进行定量划分，并根据变异系数大小划分变异程度，具体标准如表3所示.

表3 变异程度划分标准Tab.3 Classification standard of variation degree

如上所述，利用变异系数b评价上述因素的波动性，结果如表4所示. 由表4可知，滑坡高差的变异系数相对最大，属高度变异，其余四个因素相对次之，但也属中度变异，进而得出上述五个因素的分布范围均较广，也从侧面验证了三峡库区区域地质条件的复杂性.

表4 部分影响因素的特征参数统计Tab.4 Statistics of characteristic parameters of some influencing factors

由于剖面形态、坡体结构、滑体物质、滑带物质等指标只能定性分类，进而对其分布特征进行分述，具体如下.

1）剖面形态. 剖面形态对滑坡表面应力分布具有重要影响，本次共统计有四种剖面形态，其分布特征如表5 所示. 由表5 可知，凸形剖面形态所占的分布比例相对最大，达51.61%，凹形剖面形态相对最少，仅暂9.68%，总体剖面形态分布差异相对较大，对滑坡体积具有较大影响.

表5 滑坡剖面形态分布特征统计Tab.5 Statistics of distribution characteristics of landslide profile

2）坡体结构. 坡体结构能显著影响滑坡滑带位置，共将其划分为三类，分布特征如表6所示. 由表6可知，三峡库区堆积层滑坡的坡体结构以顺向坡为主，共计有16个，占51.61%，其次是逆向坡，斜交坡的分布比例相对最小，仅占12.90%.

表6 坡体结构分布特征统计Tab.6 Distribution characteristics of slope structure

3）滑体物质. 区内滑体物质主要是以第四系地层为主，主要按其颗粒大小分类，共计分为四类，分布特征如表7所示. 如表7所示，区内滑体岩性以块、碎石土为主，所占比例达54.84%，粉质黏土的分布比例相对最小，仅占6.45%，得出滑体岩性分布变化差异较大，具有较强的波动特征.

表7 滑体物质组成分布特征统计Tab.7 Statistics of distribution characteristics of material composition of sliding body

表8 滑带物质分布特征统计Tab.8 Statistics of material distribution characteristics of slip zone

根据上述，有效掌握了9个体积影响因素的分布规律，得出其分布范围均较广，具较强的波动特征，与区域地质条件的复杂性相符.

2.3 相关性分析

在前述影响因素分布特征分析基础上，该节再以相关系数为基础，评价各因素与滑坡体积间的相关程度，结果如表9所示. 可知，9个体积影响因素的相关系数并不一致，说明各影响因素对滑坡体积的影响是存在的，但影响程度存在一定差异. 其中，滑体厚度、高差及后缘高程与滑坡体积间的相关性相对最高，说明其对滑坡体积的影响相对最大；其次是坡体结构、坡面形态、坡度、滑体物质及滑带物质，这5个因素与滑坡体积属中度相关，而前缘高程对滑坡体积的影响相对较小，属低度相关. 同时，对各因素的相关等级分布比例进行统计，得Ⅲ级影响因素有3个，所占比例33.33%；Ⅱ级影响因素有5个，所占比例55.56%；Ⅰ级影响因素有1个，所占比例11.11%，得出滑坡体积影响因素的相关性等级以Ⅱ级为主.

表9 滑坡体积影响因素的相关性参数Tab.9 Correlation parameters of influencing factors of landslide volume

据上述影响因素与滑坡体积间的相关性筛选，得出各影响因素与滑坡体积的相关性以中、高相关为主，仅前缘高程的相关性相对较低，进而以8个中、高相关的体积影响因素作为后续体积预测的输入层，得滑坡体积预测模型的输入层节点数为8.

2.4 体积预测研究

根据体积预测思路，分别利用试错法、粒子群算法等优化ELM模型参数；同时，在预测过程中，先以1～26号样本为训练样本，以27～31号为验证样本.

2.4.1 参数优化分析 根据前述参数优化过程，先利用经验公式确定初步隐层节点数为13，再利用试错法求解最优核函数，得其筛选结果如表10所示. 由表10可知，四种核函数的预测精度及训练时间存在明显差异，验证了核函数筛选的必要性；同时，对比四种核函数的预测结果，得Sigmiod型核函数的平均相对误差最小，仅3.29%，训练时间也相对最短，仅34.62 ms，其次是RBF型、Hardlim型和Sine型，说明Sigmiod型核函数的预测效果相对最优，将其作为该文ELM模型的核函数.

表10 核函数优化筛选结果Tab.10 Results of kernel function optimization and screening

其次，对初步隐层节点数进行扩展，确定隐层节点数的试算区间为10～16，得其试算结果如表11 所示.不同隐层节点数对应的预测效果也存在一定差异，其中，隐层节点数为15时具有相对最优的预测精度，其平均相对误差为3.04%，训练时间仅为28.57 ms，较初步隐层节点数为13时的预测精度略有提高，不仅说明传统经验公式略显不足，也说明隐层节点数取值拓展寻优思路的正确性. 通过上述优化筛选，确定ELM模型的隐层节点数为15.

表11 隐层节点数筛选结果Tab.11 Number of hidden layer nodes filtering results

最后，在前述两参数优化基础上，再利用IPSO算法优化ELM模型的连接权值和阈值，且为对比IPSO算法的优化能力，将其预测结果与PSO算法的预测结果进行对比分析，得表12. 对比两类优化算法的预测结果，在相应验证样本处，IPSO算法具有相对略低的相对误差，且其平均相对误差为2.31%，也略低于PSO算法的2.77%，说明IPSO 算法的优化预测结果具有相对更高的预测精度，其对连接权值和阈值的优化效果相对更佳.

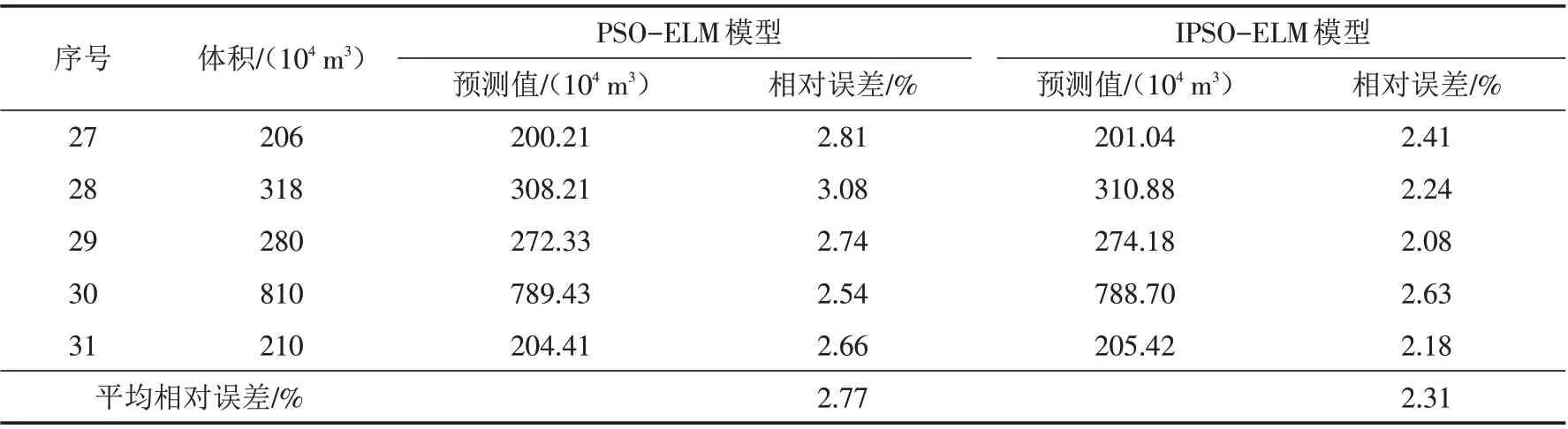
表12 参数优化后的最终预测结果Tab.12 Final prediction results after parameter optimization

2.4.2 误差弱化分析 如表12所示，IPSO-ELM模型也存在2.31%的平均相对误差，验证了预测误差弱化的必要性. 同时，通过计算得到误差序列的Lyapunov指数为1.05，大于零，说明其具有混沌特性，适用于混沌处理. 根据相空间重构弱化，得预测误差弱化后的预测结果如表13所示. 在误差弱化预测结果中，最大相对误差为2.04%，平均相对误差仅为1.71%，具有较高的预测精度，且其预测效果明显优于IPSO-ELM 模型，说明混沌理论能有效弱化预测误差，验证了该文误差弱化思路的有效性.

表13 误差弱化预测结果Tab.13 Prediction results of error weakening

2.4.3 可靠性验证分析 为进一步验证该文体积预测模型的有效性，再以1～5号样本为可靠性验证样本，对其进行预测研究，得其预测结果如表14所示. 在可靠性验证过程中，最大相对误差为1.69%，平均相对误差也仅为1.49%，与前述预测结果相当，得出该文预测模型不仅具有较高的预测精度，还具有较高的可靠性.

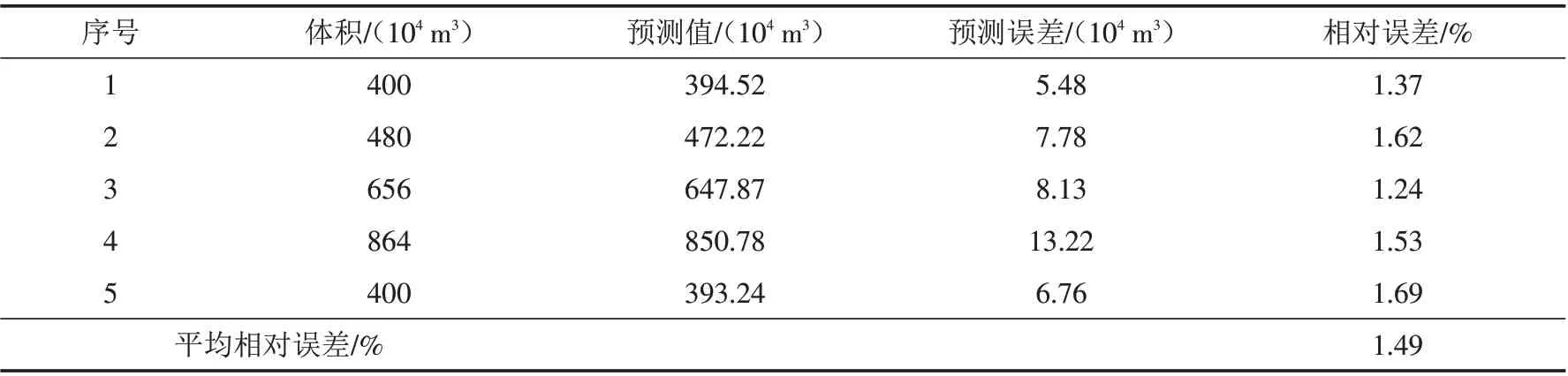
表14 可靠性验证样本预测结果Tab.14 Prediction results of reliability verification samples

根据上述，得出通过递进优化不仅可以有效提高预测精度，还能节约运算时间，验证了混沌优化极限学习机在滑坡体积预测中的适用性，值得推广应用研究.

3 结论

通过三峡库区滑坡体积影响因素的分布特征分析及预测研究，主要得出如下结论：

1）库区滑坡体积影响因素较多，主要包括滑坡空间位置因素和滑坡特征因素，且各类影响因素的分布范围均较广，具有较强的波动特征，与区域地质条件的复杂性相符.

2）传统ELM模型参数具一定的随机性，通过试错法、IPSO算法等能有效优化模型参数，不仅能有效提高预测精度，还能节约运算时间，验证了该文优化方法的适用性和有效性.

3）混沌理论能有效弱化预测误差，所得预测结果的预测精度较高，验证了混沌优化极限学习机在滑坡体积预测中的有效性，且通过可靠性验证分析，得出该文预测模型具有较高的预测精度和可靠性.