基于ADINA堆积层滑坡地震作用下动力响应特性及稳定性研究

朱永和， 邓伟杰， 赵顺利

（黄河勘测规划设计研究院有限公司，郑州 450000）

我国是发生地质灾害最多的国家之一，复杂的地形地貌、多样地质构造组合是发生地质灾害的内因；人为不合理利用自然资源是促使自然灾害发生的外因. 另一方面全球化恶劣气候的自然因素是地质灾害的导火线. 据相关部门不完全统计，2003年到2015年我国地质灾害有30万次，滑坡发生的次数为22万次，由地震作用引起的滑坡发生次数有11万次，地震作用引起的滑坡发生次数占滑坡发生总次数50%，占地质灾害发生总次数的36.6%. 由地震造成生命财产和经济损失不计其数，因此对滑坡在地震作用下进行动力响应和稳定性分析意义重大［1-2］. 近年来众多学者对滑坡在地震作用下的动力响应特征和变形机制做了较多研究. 何蕴龙［3］采用有限元动力分析法分析了岩石边坡地震动力系数分布规律；言志信［4］通过有限差分软件FLAC3D对顺层岩质边坡动力响应规律及变形机理进行了研究；徐光兴［5］采用大型振动台模型试验探讨地震动参数对岩体边坡动力特性和动力响应的影响. 目前对堆积层滑坡的动力响应特性和稳定性研究还处在初级阶段，因此本文基于ADINA动力有限元法软件计算典型堆积体滑坡在地震作用下的动力响应特征，分析地震作用下的静力法和动力分析法的可行性［5-7］.

1 工况

研究区位于四川广安市邻水县高滩镇，属于侵蚀地貌深丘区，地形较平缓，由间歇性面状抬升运动形成多级夷平面和河流堆积阶地. 滑坡位于华釜山大断裂带附近，以背斜挤压紧密向斜舒缓为主形成典型的隔挡式地质构造. 据勘察结果表明，研究区主要出露地层有中生界侏罗纪中统( J2s) 上沙溪庙组地层和第四纪全新统( Q4)松散堆积层，其中侏罗纪中统上沙溪庙组地层是呈褐黄色、棕黄色，并以石英及黏土矿物为主，泥钙质胶结，中厚层—厚层状构造泥质粉砂岩，岩层总体产状为290°∠20°. 堆积层滑坡体主要为第四纪堆积土组成，耕土()灰色，以黏性土为主，富含植物根系；粉质黏土()为褐黄色、褐红色，由黏粒和粉粒组成分，布于基岩顶板之上，其底部可见母岩颗粒. 滑坡体主要是第四纪堆积层粉质黏土沿滑床泥质粉砂岩接触面向下滑动而成，据勘探资料表明，滑坡体底部有一弧形软弱结构面，埋深随滑坡体厚度变化而变化.雨水和地表水的补给使地下水位不断增高，减弱了滑坡体抗剪强度. 近几年发生的地震作用很大程度上改变了岩体的结构特性，为水的渗透提供了天然通道，严重影响滑坡稳定性.

滑坡属于牵引式堆积层滑坡，平面呈圈椅状，坡面呈阶梯状，如图1所示. 滑坡潜在滑移方向为5°，地形坡度一般为25°～30°，总体坡度为26.5°. 坡体纵向长约56 m，横宽约42 m，前缘高程294 m，后缘高程322 m，滑体面积约2.35×103m2，厚约1.0～7.5 m，滑体体积约9.4×103m3.

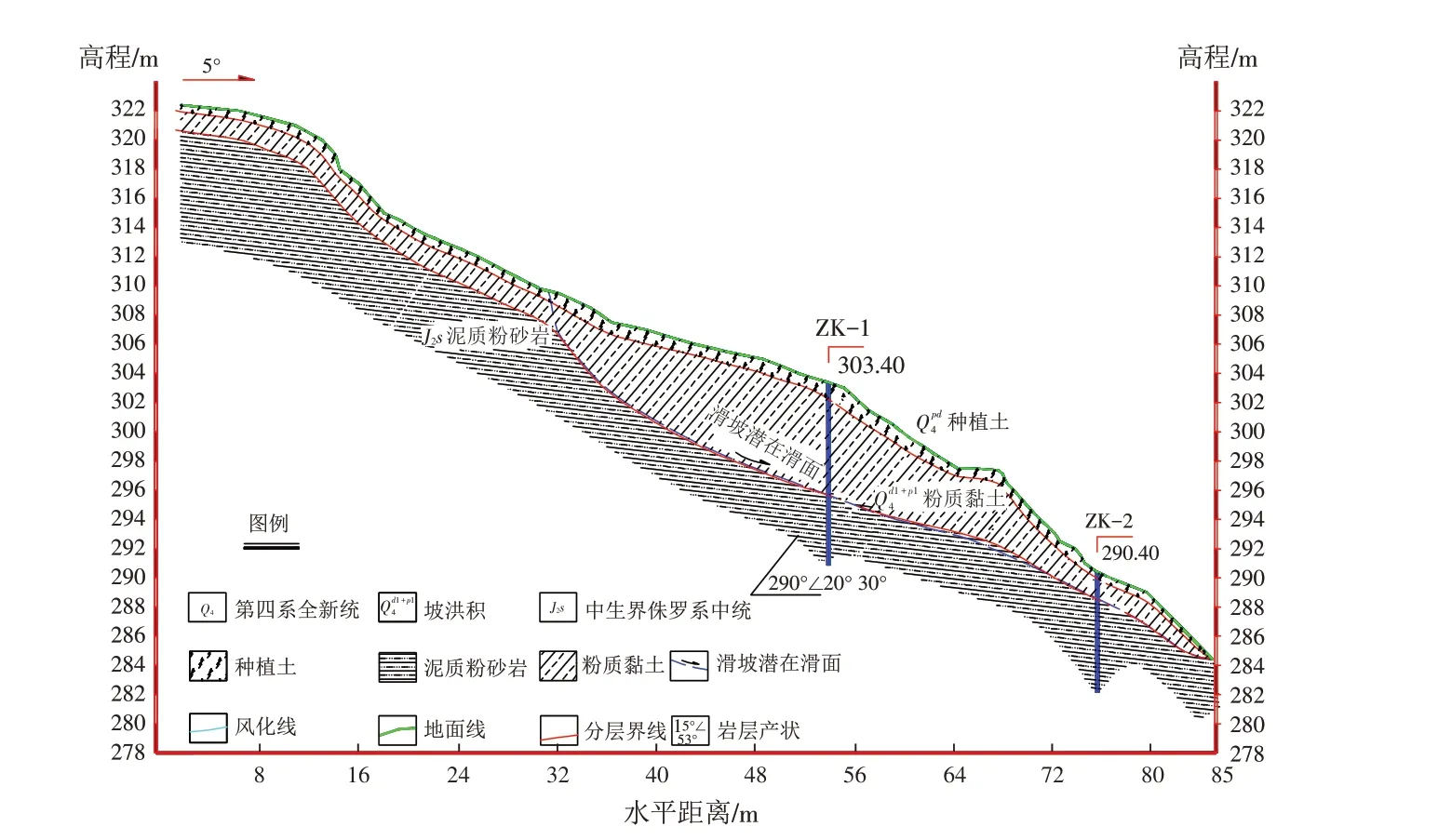
图1 滑坡地质剖面图Fig.1 Geological profile of landslide

2 计算模型建立

2.1 滑坡模型

基于ADINA软件建立动力有限元计算模型，研究滑坡在地震作用下破坏的发生和发展过程，判断滑坡的稳定性及其发展趋势［8-11］. 根据滑坡体地质构造和地层岩性建立滑坡有限元概化模型，地层岩性从表面依次分为：第四纪种植土、第四纪残坡积粉质黏土、侏罗系中统中风化泥质粉砂岩. 按其岩性分为三种材料，均是基于摩尔-库伦准则的理想弹塑性材料. 边界条件设定为：两侧为Y向约束，底边为完全固定. 模型采用四节点进行剖分，共3 个5038 节点，4908 个单元，具体见图2.

2.2 计算条件与参数设置

本计算参数是根据室内试验数据和勘查分析成果，结合类似工程经验和工程地质手册后，选取滑坡体物理力学参数值，见表1.

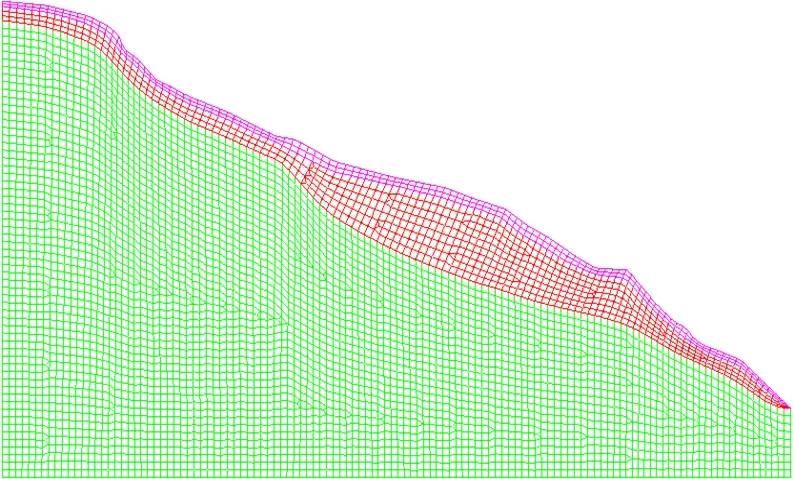
图2 有限元网格剖分图Fig.2 Finite element mesh subdivision

表1 滑坡体岩土体物理力学参数Tab.1 Physical and mechanical parameters of landslide rock mass

根据勘察报告，研究区地震烈度为VII度，地震峰值加速度0.15 g. 故模拟动力分析时采用最大峰值为0.84 m/s2的Kobe 波进行，具体见图3，模拟时间为10 s.

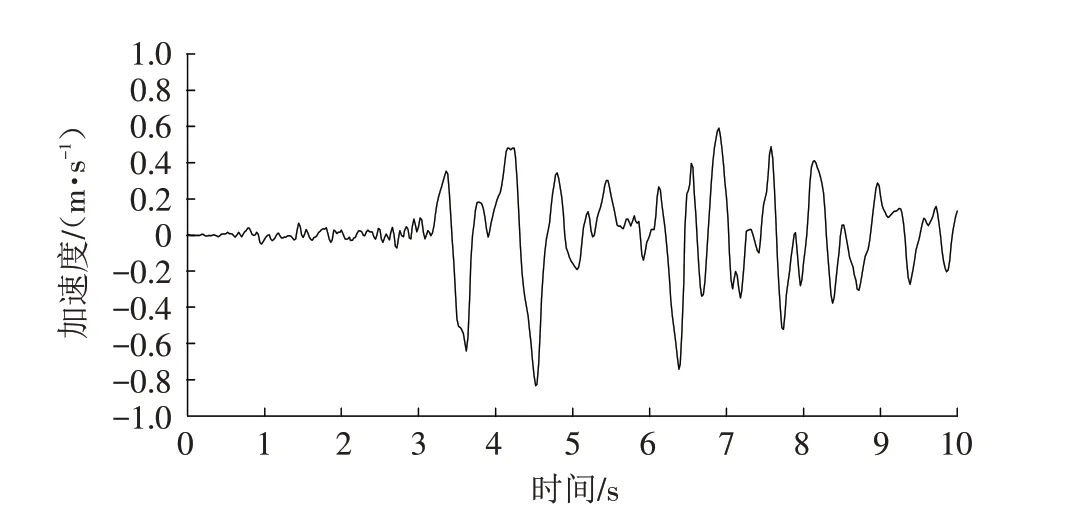
图3 地震加速度时程曲线Fig.3 Seismic acceleration time curve

3 堆积层滑坡动力响应及稳定性分析

3.1 堆积层滑坡动力响应分析

为准确地模拟出滑坡体在地震作用下的位移、加速度、应力和应变随时间的变化，在滑坡体前缘、中部、后缘各设置3个监测点，每个部位的3个监测点依次是从坡体表面垂直向下等间隔取［12-14］. 前缘设置监测节点由上而下依次为节点6214、节点5892、节点4904；中部监测为节点4874、节点4386、节点4471；后缘监测为节点4844、节点4490、节点2694.

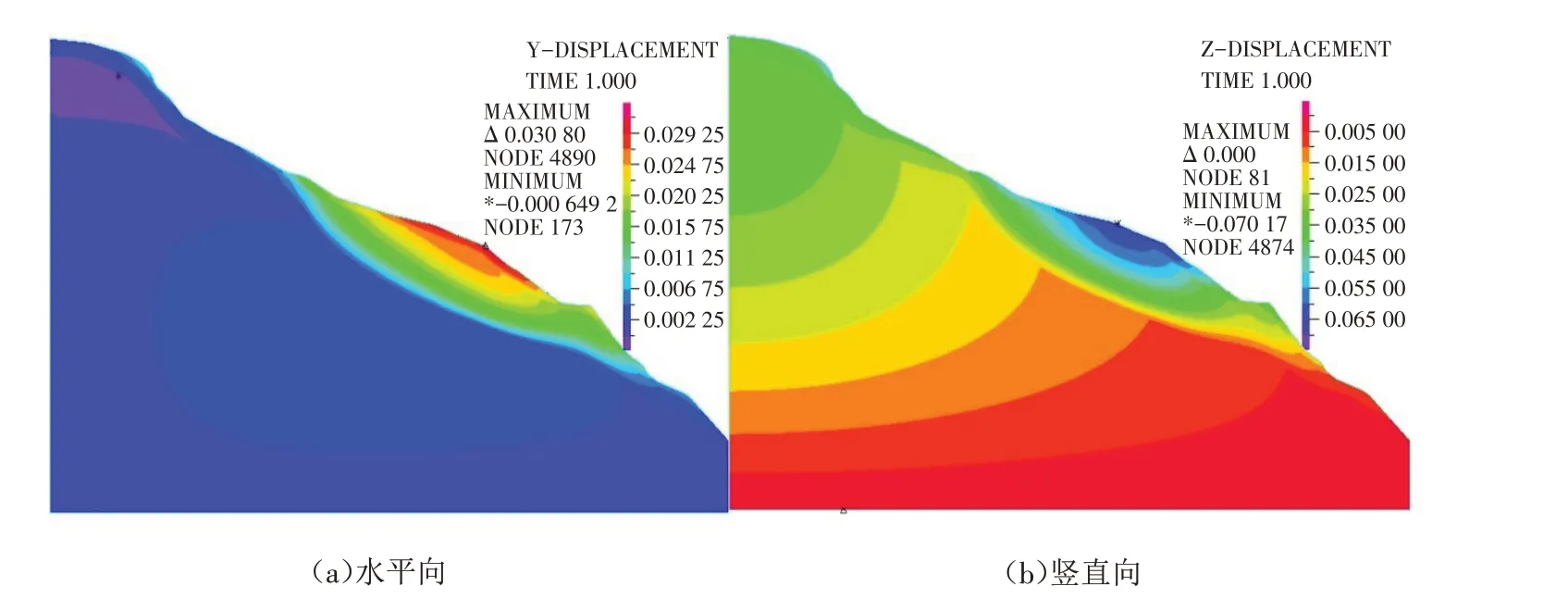
图4 拟静力作用下位移云图Fig.4 Displacement clouds under quasi-static action

3.1.1 位移、加速度响应规律分析 滑坡变形是多种影响因素下的结果，通过有限元法计算出滑坡的不同方向位移来确定滑坡的稳定状态［16］.图4（a）、（b）分别是地震作用下静力水平位移、竖向位移云图. 由图4可知，静力作用下滑坡最大水平位移3.08 cm，在滑坡中部；最大竖向位移为7.02 cm，分布滑坡表层距破顶1/3处中后部. 图5（a）、（b）分别是地震动力作用下水平位移、竖向位移云图. 由图5可知，动力作用下水平位移增大为4.45 cm，在滑坡后缘处；竖向位移增大为9.15 cm，在滑坡中部. 动力作用模拟出位移结果和现场勘查滑坡后缘出现多处拉伸裂缝相符合.

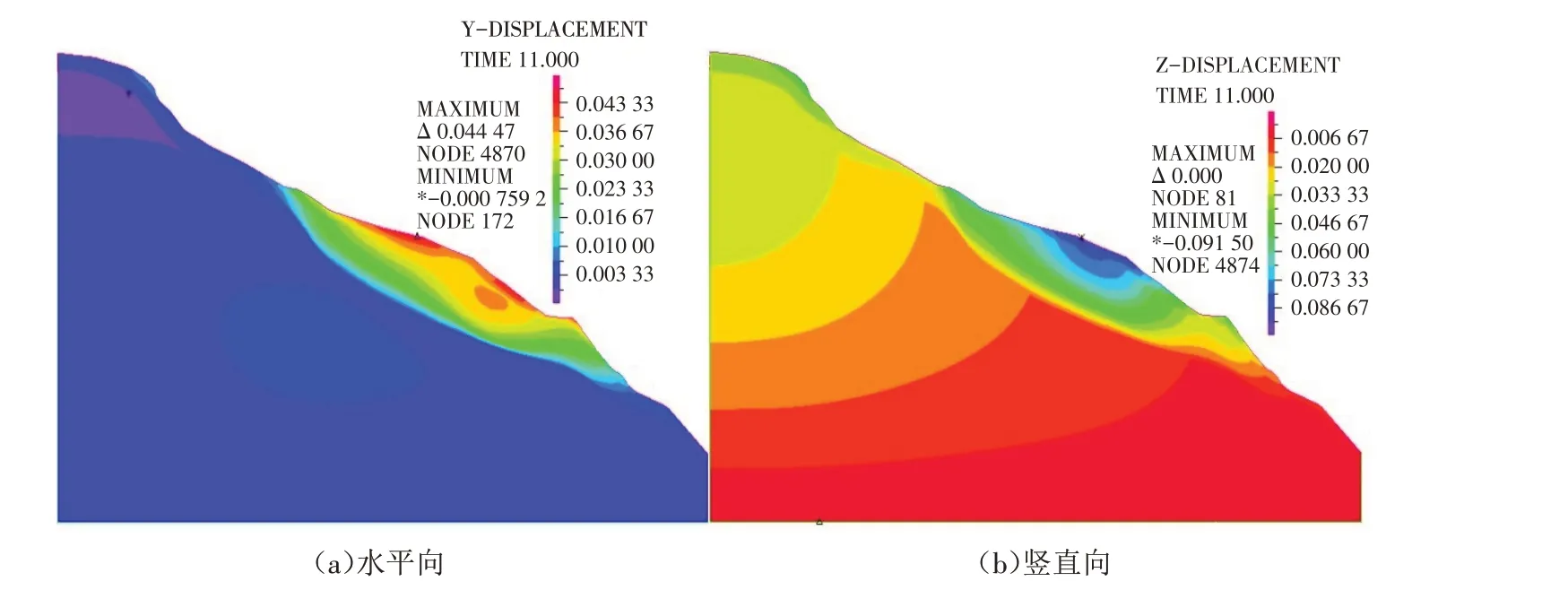
图5 动力作用下位移图Fig.5 Displacement cloud diagram under dynamic action

为体现动力作用对滑坡的影响，取坡体前缘6124节点、中部4874、4386、4471节点和后缘4844节点作为位移响应节点，计算出滑坡不同部位监测点位移响应曲线（图6）、滑坡中部不同高程监测点位移响应曲线（图7）. 地震波在滑坡体介质中通过岩土体的结构、节理、裂隙等构造改变了地震波的能量，促使滑坡前缘、中部和后缘发生变形破坏.

如图6 所示，在地震动力持续10 s 作用下坡体发生位移显著，其中坡体中部节点4874位移最大，前缘节点6124 位移最小，后缘位移居中. 滑坡中部监测点的位移时程曲线振幅较滑坡前缘和后缘都有明显放大、滞后现象. 如图7 所示，在动力作用下坡体中部随着监测点高程的增加，位移时程曲线振幅不断增大，位移峰值点在基本相同的时间点上. 这说明滑坡体中不同位移的位移响应基本一致，说明在动力作用下滑坡体的各部位是同步变化的.

加速度可以用来表示地震力，通过绘制坡面和坡体内监测点的加速度响应曲线来观察滑坡体对动力地震波的响应规律. 由图8 所示，在坡体表面从坡体前缘、坡体中部到坡体后缘，监测点加速度的振幅递增，中部表面节点4874地震加速度极值可达6.0 m·s-2. 由图9可知，基岩体内监测点4471 加速度变化较小，在滑带处节点4386加速度变化明显增大，坡体表面加速度振幅最大. 堆积层内部加速度变化幅度不明显，但越接近坡体表面加速度变化越大，即是坡体对地震波的放大效应.

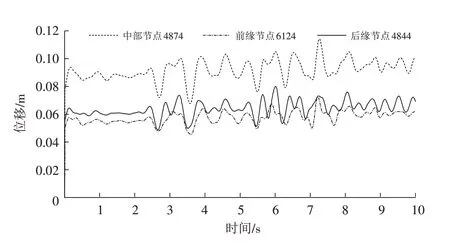
图6 滑坡不同部位监测点位移时程曲线Fig.6 Displacement-time curve of monitoring points in different parts of landslide

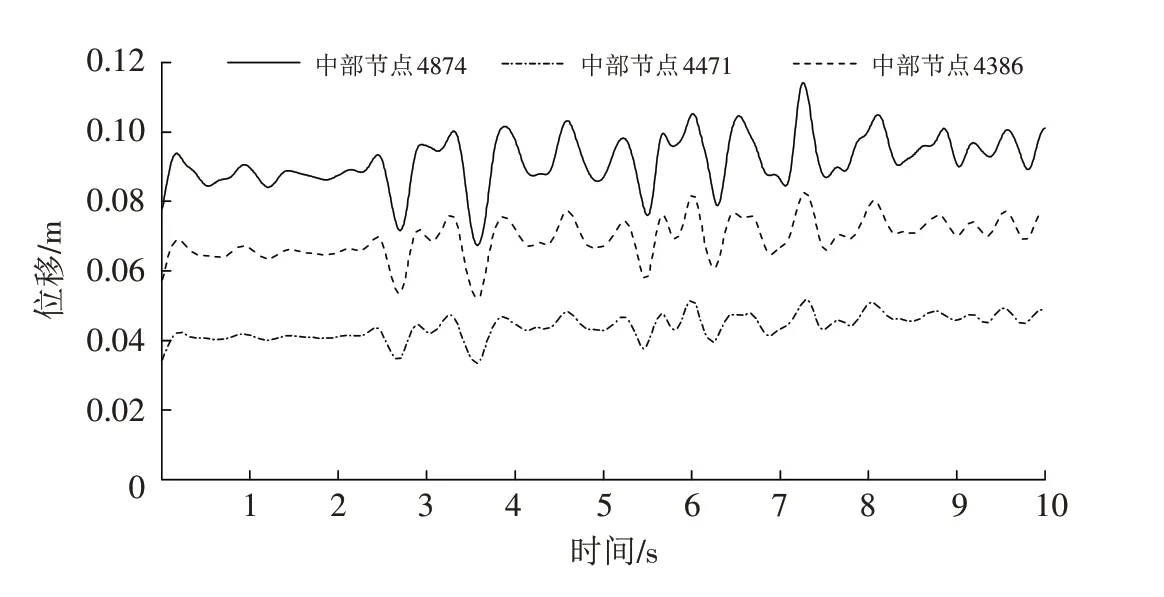
图7 滑坡中部不同高程监测点位移时程曲线Fig.7 Displacement-time curve of different elevation monitoring points in the middle of the landslide

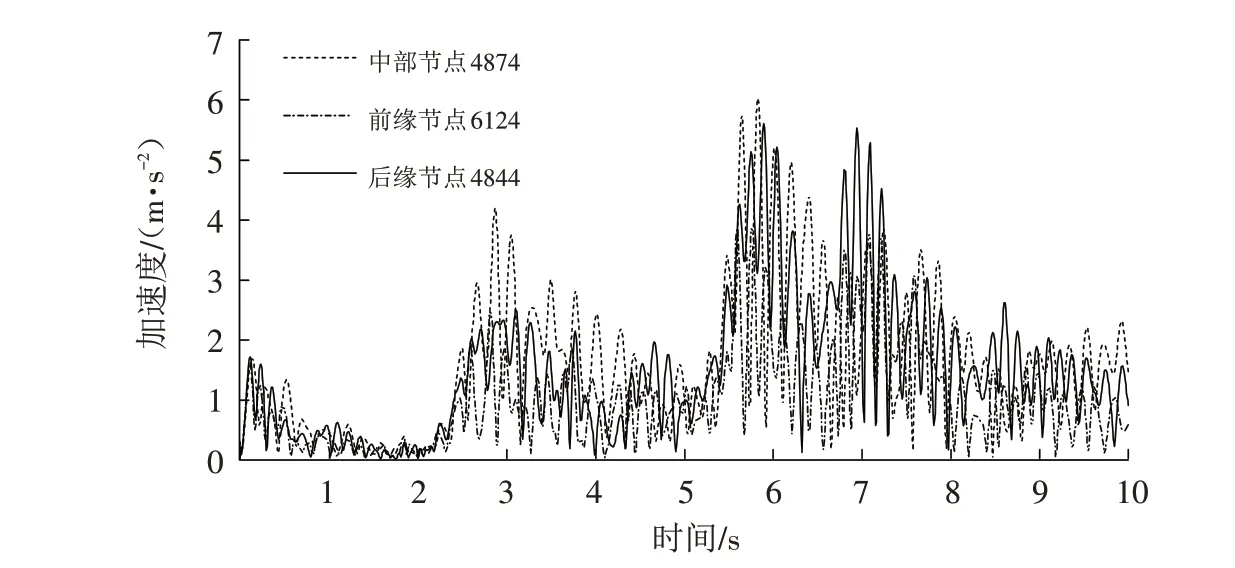
图8 滑坡不同部位监测点加速度时程曲线Fig.8 Acceleration-time curve of the monitoring points in different parts of the landslide

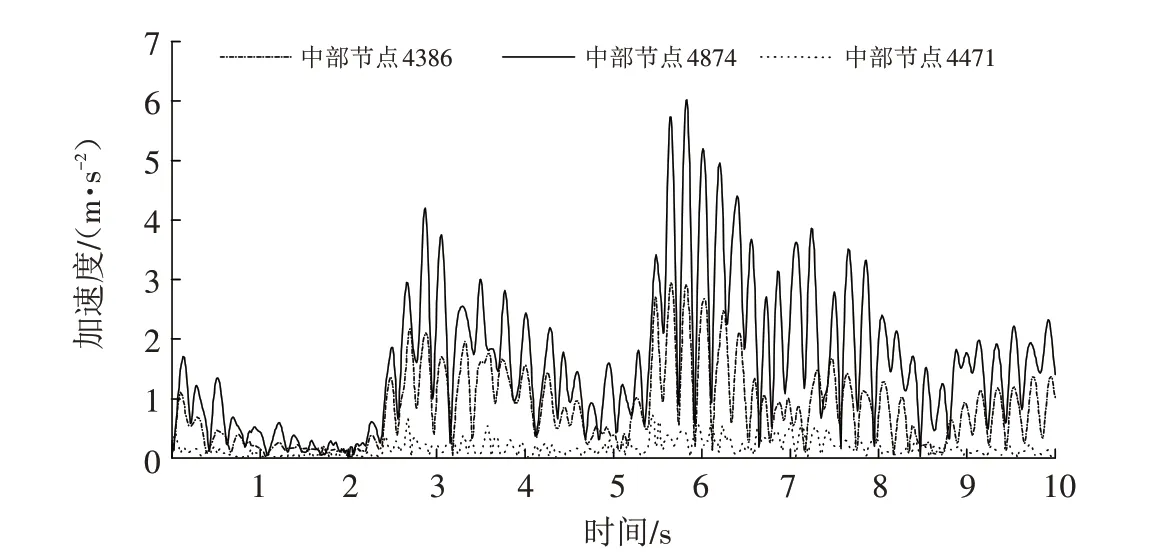
图9 滑坡中部不同高程监测点加速度时程曲线Fig.9 Displacement-time curve of different elevation monitoring points in the middle of the landslide

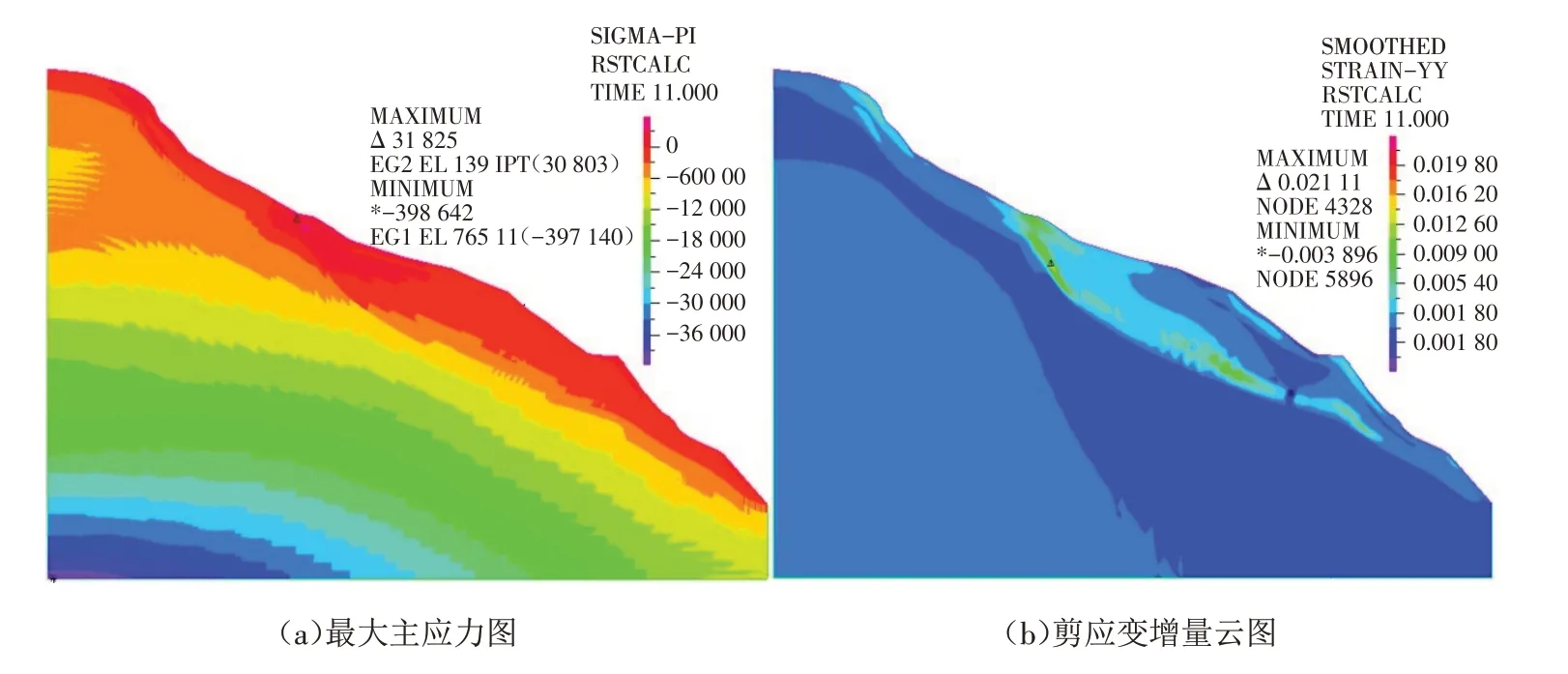
图10 动力作用下应力、应变增量云图Fig.10 Stress and increase strain cloud diagram under dynamic action

3.1.2 应力、应变响应规律 图10为动力作用下的应力、应变增量云图，图中压应力为正，拉应力为负. 由图10（a）可以看出，堆积层滑坡在地震动力作用下的最大压应力在基岩内部值为398.64 kPa；拉应力分布在坡体表层，最大拉应力31.83 kPa主要分布在后缘处，与现场勘查中后缘出现多处拉裂隙相吻合. 图10（b）是滑坡在动力作用下剪应变增量的云图，可知滑坡后缘出现最大剪应变为2.11×10-4，前缘处出现压裂破坏剪应变为3.89×10-3. 图中明显看出贯通区，即滑坡潜在滑动面，这一区域表明剪应变从坡脚开始向坡体内部扩散直到后缘，当塑性区贯通时滑坡将处于不稳定状态.

3.2 堆积层滑坡稳定性分析

有限元计算边坡的稳定性系数时通常运用的是强度折减法［16］，通过不断降低岩土体的抗剪强度指标直到岩土体达到临界破坏状态，然而岩土体不断折减的系数即为边坡稳定系数. 动力分析滑坡的稳定系数时是计算不同时刻下的稳定系数，并求取平均稳定系数. 采用特征点位移突变和塑性区贯通判据相结合的方法作为滑坡失稳依据，从而计算出动力作用下不同时刻的稳定系数.

基于拟静力通过强度折减法计算出滑坡折减系数为1.06，动力分析计算出的平均稳定系数为0.98，综合对比分析刘家滑坡在地震作用下处于不稳定状态. 因此动力分析计算出滑坡稳定状态更符合情况，具有一定的理论指导意义［17-19］.

4 结论

1）通过ADINA软件模拟对刘家滑坡在动力地震作用下不同监测点的位移、加速度的响应及其之间规律进行了分析，动力分析出水平位移和竖向位移都有所增加，其中最大竖向位移9.15 cm出现在后缘处. 滑坡中部监测点的位移时程曲线振幅较滑坡前缘和后缘都有明显放大、滞后现象. 随着监测点高程的增加，位移时程曲线振幅不断增大，位移峰值点基本同步. 在坡体表面从坡体前缘、坡体中部到坡体后缘，加速度的振幅递增，坡体中部地震加速度极值可达6.0 m·s-2.

2）通过动力响应研究，获得滑坡体不同部位的应力、应变的响应分析及其之间规律；滑坡后缘出现较大拉应力，易出现拉裂缝. 滑坡前缘发生压裂破坏，剪应变增量为3.89×10-3. 剪应变增量从坡脚开始向坡体内部扩散直到后缘，对坡脚应着重防护.

3）通过拟静力和动力分析计算出的滑坡稳定系数的对比分析表明，滑坡处于不稳定状态. 堆积层滑坡动力作用下稳定性分析具有一定必要性.