类方柱的气动性能和流场特性

杜晓庆 ，刘延泰 ，董浩天 ，施定军

（1.上海大学 土木工程系，上海200444；2.上海大学 力学与工程科学学院，上海200444；3.上海大学 风工程和气动控制研究中心，上海200444）

大长细比方形截面柱体结构在土木工程中有广泛应用，如超高层建筑和大跨度缆索承重桥的索塔，其抗风问题是结构设计的关键[1-4].气动控制措施是一种经济、有效的抗风设计方法，适当的气动措施可有效减小风荷载和风致响应，因而方柱的气动性能优化得到研究者的广泛关注[5-8].

超高层建筑的气动控制措施包括截面的角部处理、截面形状改变、沿高度的形状或尺寸变化等[9-13].Tanaka等[14-16]对角部处理、截面形状的优化和沿高度的形状或尺寸变化的模型进行了风洞试验，对比分析了不同气动外形柱体的倾覆力矩系数、风力响应等结果.

针对方形截面柱体，常用的平面形态气动优化措施为角部修正，包括圆角、倒角、切角等形式，这类气动措施可有效优化方柱结构的受力与风致振动问题[17].Tamura及其合作者[18-20]对标准方柱、圆角、切角方柱进行了数值模拟和风洞试验，结果表明，圆角和切角措施可以削弱涡脱强度，减小平均阻力和脉动升力系数.文献[21-26]中研究了圆角、切角、凹角等角部修正对方柱风致响应的影响，研究表明，3种角部措施中，圆角化方柱能最有效地抑制柱体的横风向响应.

对于圆角化方柱，圆角率会对柱体气动性能产生很大影响.Delany等[27]通过风洞试验研究R/B=1/50、1/6、1/3（R为模型圆角半径，B为模型名义边长）3种圆角率方柱气动力的雷诺数效应.Carassale等[28-29]针对R/B=0、1/15、2/15等3种圆角率的方柱模型，通过风洞试验研究了来流湍流度和雷诺数对其气动性能的影响.Zhang等[30]则通过数值模拟研究了低雷诺数（Re=1 000）下 R/B=0、0.125、0.250、0.375、0.5等5种圆角率方柱的流场特性和气动性能.杜晓庆等[31]对R/B=1/7的圆角方柱进行大涡模拟研究，解释了圆角化对方柱气动性能影响的流场机理.

从以往研究看，方柱平面形态的修正局限在角部处理气动措施，但随着超高层建筑的大量建设，出现了不少角部修正与凸边、凹边等形状相结合的类方柱结构，而目前尚未见到研究此类方柱气动性能和流场特性的文献.基于上述考虑，本文采用大涡模拟方法，在雷诺数为2.2×104时，以角（尖角、圆角）、边（直边、凸边和凹边）形状修正的类方柱为研究对象，研究了16种类方柱的气动性能和流场特性，以及凸边圆角柱的气动性能随边部曲率半径的变化规律，分析了角、边形状的改变对柱体气动性能的影响，并从流场角度探讨了形状修正对方柱气动性能的作用机理.

1 数值方法和计算模型

1.1 流动控制方程和亚格子模型

在大涡模拟（LES）方法中，大尺度涡通过滤波后的Navier-Stokes方程直接求解，而小尺度的涡则采用亚格子尺度模型（SGS）模拟.经过滤波函数的滤波，可得到大尺度涡的不可压缩Navier-Stokes方程：

式中：ui为滤波后速度分量；ρ为流体密度；p为滤波后压力；ν为流体动力黏度；τij为亚格子应力张量.

亚格子应力τij采用WALE亚格子尺度模型，WALE亚格子尺度模型具有以下形式：

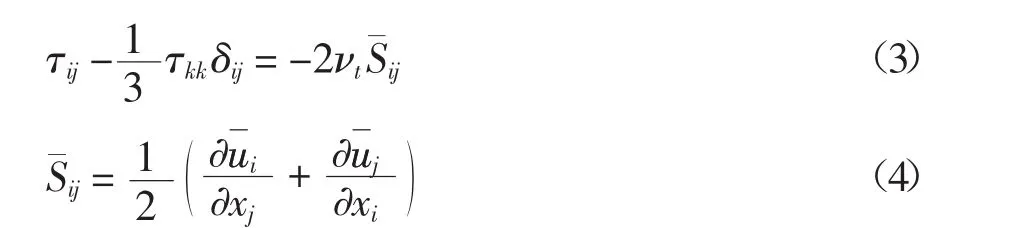
式中：νt是亚格子尺度的湍动黏度，在WALE模型中

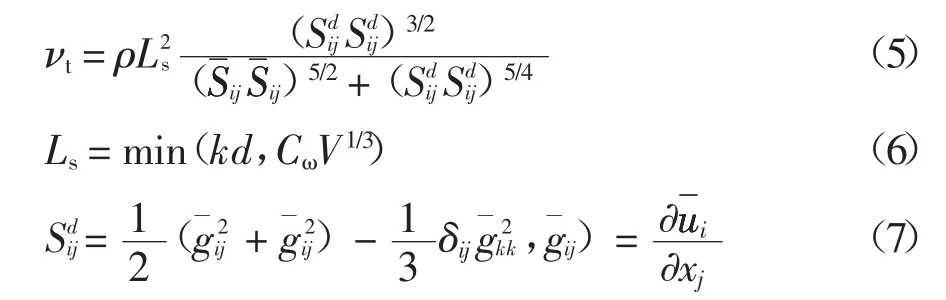
本文采用的WALE常数Cω是0.325，此为Fluent默认值，该取值下可取得比较满意的结果.计算采用SIMPLEC格式求解压力速度耦合方程组，空间离散采用中心差分格式，时间离散采用二阶全隐格式.

1.2 计算模型和计算域

图1为以凸边圆角柱为例的计算模型示意图.均匀来流速度为U，来流湍流度为0，所有模型的截面面积相等，即面积S=B2（其中B为计算模型的名义边长），风向角为0°，雷诺数为2.2×104（根据模型名义边长B和来流风速U计算得到）.模型的圆角半径定义为R，边部曲率半径定义为K.

图1 计算模型示意图Fig.1 Sketch of computational model

本文考虑了2种角部形状，其角部半径R/B=1/100和1/7（文中分别称为尖角和圆角）；考虑了3种边部形状，即直边、凸边、凹边.图2是本文所选取的6种截面类方柱，分别命名为：直边尖角柱（标准方柱）、凹边尖角柱、凸边尖角柱、直边圆角柱、凹边圆角柱和凸边圆角柱，边部曲率半径均为K/B=2.5.图3是本文所选取的部分不同曲率半径的凸边圆角柱模型示意图，本文考虑的曲率半径K/B=0.564（圆柱）、0.7、0.8、1.0、1.2、1.25、1.3、1.35、1.4、1.5、2.5、∞（直边圆角柱）.

计算模型的整体网格和角部局部网格放大图见图4.由图4（a）可见，入口边界圆弧顶点距离方柱中心为20B，方柱中心距离出口边界距离为30B，横风向计算域宽度为40B，计算域高度（方柱展向长度H）为4B，阻塞率为2.5%.计算域采用速度入口边界条件，自由出口边界，两侧采用对称边界条件，展向采用周期性边界条件，方柱表面为无滑移壁面边界条件.

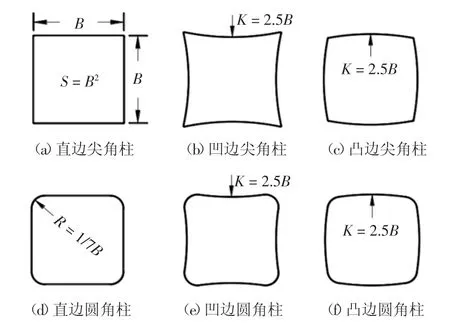
图2 6种柱体的截面形状Fig.2 Sectional configuration of six cylinders

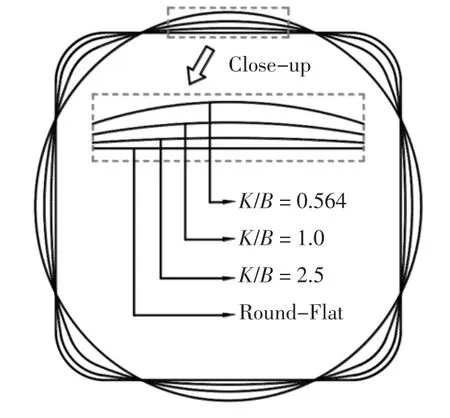
图3 不同边部曲率半径下的柱体Fig.3 Cylinders with different K/B

2 计算参数和结果验证

本文以标准方柱为研究对象，在文献[31]的基础上进行计算模型的结果验证，结果如表1和图5所示.文献[31]中，网格验证所采取模型展向长度为2B，为提高网格精度，本文以展向长度4B进行模型验证，且验证计算时间步和展向长度的参数范围更大.

与文献[31]网格验证部分相一致，分别考察了不同周向网格数量、计算时间步、展向长度和展向网格尺度对方柱气动性能计算结果的影响.本文方柱周向网格数的取值为120、200和320；无量纲时间步长Δt*= ΔtU0/B（其中 Δt为有量纲时间步，U0为来流风速），为 0.005、0.010、0.025 和 0.030；展向长度 H 为1B、2B、4B 和 6B；展向网格尺度为 0.15B、0.1B 和0.075B.

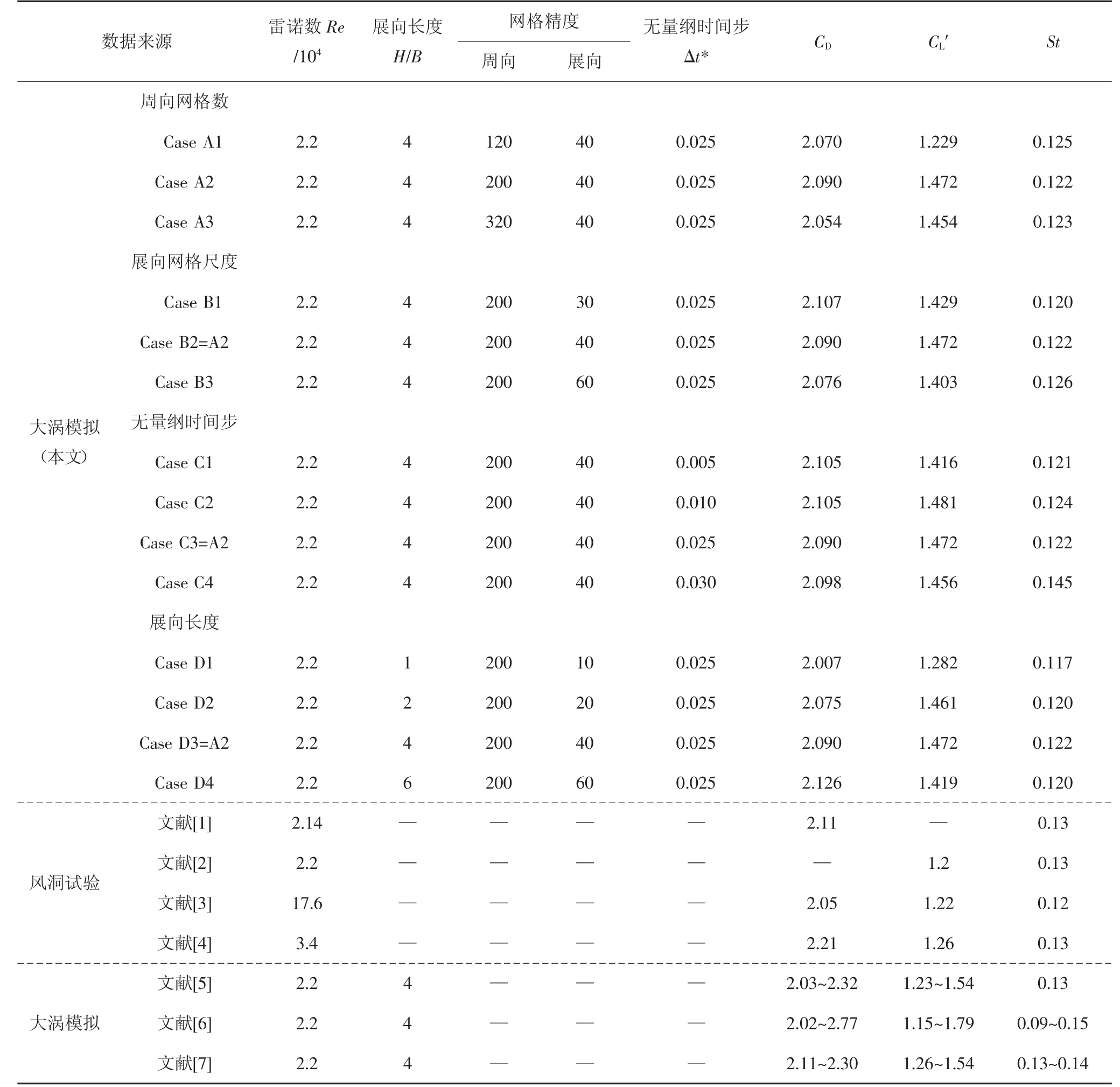
表1 α=0°标准方柱计算结果及其验证Tab.1 Present results of sharp corner square cylinders for α =0°and their comparison with previous data

图4 计算模型平面网格Fig.4 Plane computation grid scheme

由表1和图5可得，周向网格数量、计算时间步和展向网格尺度对计算结果的影响与文献[31]中的分析相似，故本文所采取的周向网格数量、计算时间步和展向网格尺度与文献[31]相一致，即周向网格数为200，无量纲时间步为0.025，展向网格尺度为0.1B.在工况A2的基础上，选取展向长度为1B、2B、4B、6B进一步研究展向长度的影响.比较表1中本文计算的各个工况，方柱展向长度为1B时，得到的气动力系数整体均偏小，对比长度为2B、4B和6B的计算结果，可以发现：随着展向长度的增大，平均阻力系数增大，脉动阻力系数和St数变化不大，其中展向4B和6B时平均阻力系数与文献中的风洞试验结果和大涡模拟结果更为相近.

图5 α=0°标准方柱表面风压系数Fig.5 Pressure coefficient distribution of sharp corner square cylinders for α =0°

综合考虑结果精度和计算资源，下文工况所选取的计算模型参数均与工况A3相近，即展向长度为4B，展向网格尺寸为0.1B，周向网格数为200，角部网格加密；近壁面最小网格厚度为0.001B，壁面附近沿径向的网格增长率为1.06，近壁面y+≈1，满足大涡模拟对近壁面的网格精度要求；无量纲时间步Δt*为0.025.

3 角边形状的影响

3.1 气动力系数和St数

图6给出了6种柱体的气动力系数和斯托罗哈数数的对比情况.总体上看，与标准方柱相比，只有凹边尖角柱的气动力系数升高，其余柱体的气动力系数均有一定程度的降低，凸边圆角柱的气动力系数均最小.

由图6（a）可知，与标准方柱相比，凹边尖角柱的脉动阻力系数升高，其余柱体的脉动阻力系数降低，且凸边圆角柱脉动阻力系数最小；与角部为尖角的柱体相比，圆角化柱体的脉动阻力系数显著降低；与直边柱体相比，凸边柱体的脉动阻力系数升高，凹边柱体降低.分析图 6（b）和 6（c）可得，角、边形状对脉动阻力和脉动升力系数的影响跟平均阻力系数的变化趋势一样.

从图6（d）可见，角、边形状对斯托罗哈数的影响与3种气动力系数的变化趋势相反.与标准方柱相比，凹边尖角柱的斯托罗哈数降低，其余柱体升高，且凸边圆角柱的斯托罗哈数最大，即6种柱体中凸边圆角柱的涡脱频率最大.

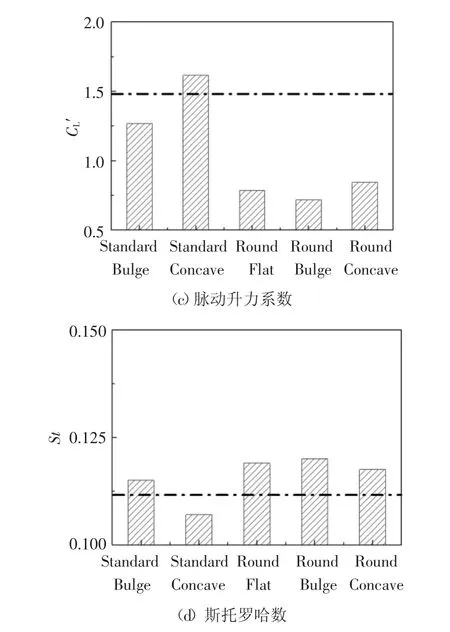
图6角边形状对气动力系数和斯托罗哈数的影响Fig.6 Effect of corner and edge shape on aerodynamic coefficients and Strouhal number

3.2 平均和脉动风压系数

图7 分别为6种柱体的表面平均风压和脉动风压系数分布图.总体上看，各柱体表面风压系数分布曲线整体趋势相近，但数值差异较大，特别是脉动风压系数.

由图 7（a）可见，迎风面（ab）上，各柱体平均风压系数基本一致；在上、下侧面（bc和ad）和背风面（cd），与角部为尖角的柱体相比，圆角化柱体平均风压系数绝对值均减小，3种圆角化柱体平均风压系数相差不大；对于3种尖角柱体，不同边部形状下，各柱体的平均风压系数在背风面角点（c点和d点）出现一定的差异，且凹边尖角柱的角点负压绝对值最大，其余位置则较为接近.分析图7（b）可知，角、边形状对柱体脉动风压系数的影响与平均风压系数的变化趋势基本一致.

3.3 平均风压场

图8给出了0°风向角下6种柱体的时间平均风压场.由图8可见，与直边柱体相比，凸边柱体上、下侧面及尾流区负压强度减弱，负压极值减小，这是凸边柱体平均阻力系数较小的主要原因；凹边柱体的平均风压场变化趋势与凸边柱体相反；尾流区风压场的差异是造成各柱体平均阻力系数不同的主要原因.此外，与角部为尖角的柱体相比，圆角化柱体的上、下侧面和尾流区负压强度大大减小.

从总体上看，6种柱体中，凸边圆角柱尾流区域负压绝对值最小，可见凸边修正和圆角措施的组合能最有效地减弱柱体周围平均风压场.

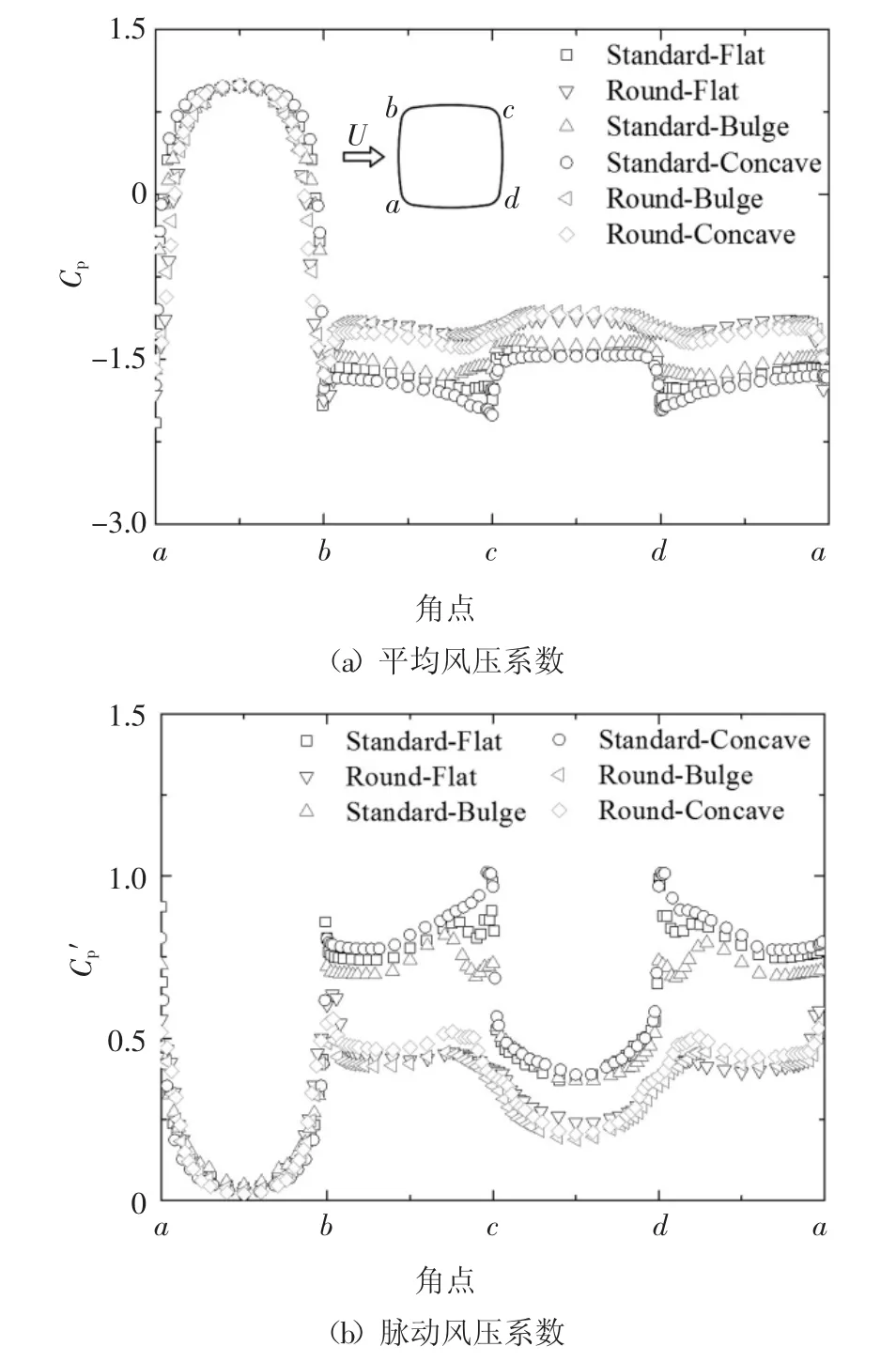
图7角边形状对表面风压系数的影响Fig.7 Effect of corner and edge shape on pressure coefficients

3.4 平均流态结构

图9 是6种柱体绕流场的时间平均流线图.总体上看，气流在各柱体迎风面角点（a点和b点）发生分离，并在柱体上、下侧和尾流中形成6个回流区，侧面和尾流的回流区在方柱的背风面角点附近连通.

由图9可见，与直边柱体相比，凸边柱体上、下侧回流区范围减小，气流分离后的剪切层更贴近柱体侧面，而凹边柱体变化趋势相反；即边部形状的改变主要影响柱体上、下侧边的流场结构.与角部为尖角的柱体相比，圆角化柱体上、下侧回流区范围显著减小，剪切层更贴近柱体侧面，尾流长度增大，宽度减小.

从总体上看，6种柱体中，凸边圆角柱上、下侧回流区范围最小，尾流长度最大，尾流宽度最小，这导致了凸边圆角柱受到最小的平均阻力系数，尾流的差异是造成各柱体的平均阻力系数不同的主要原因.

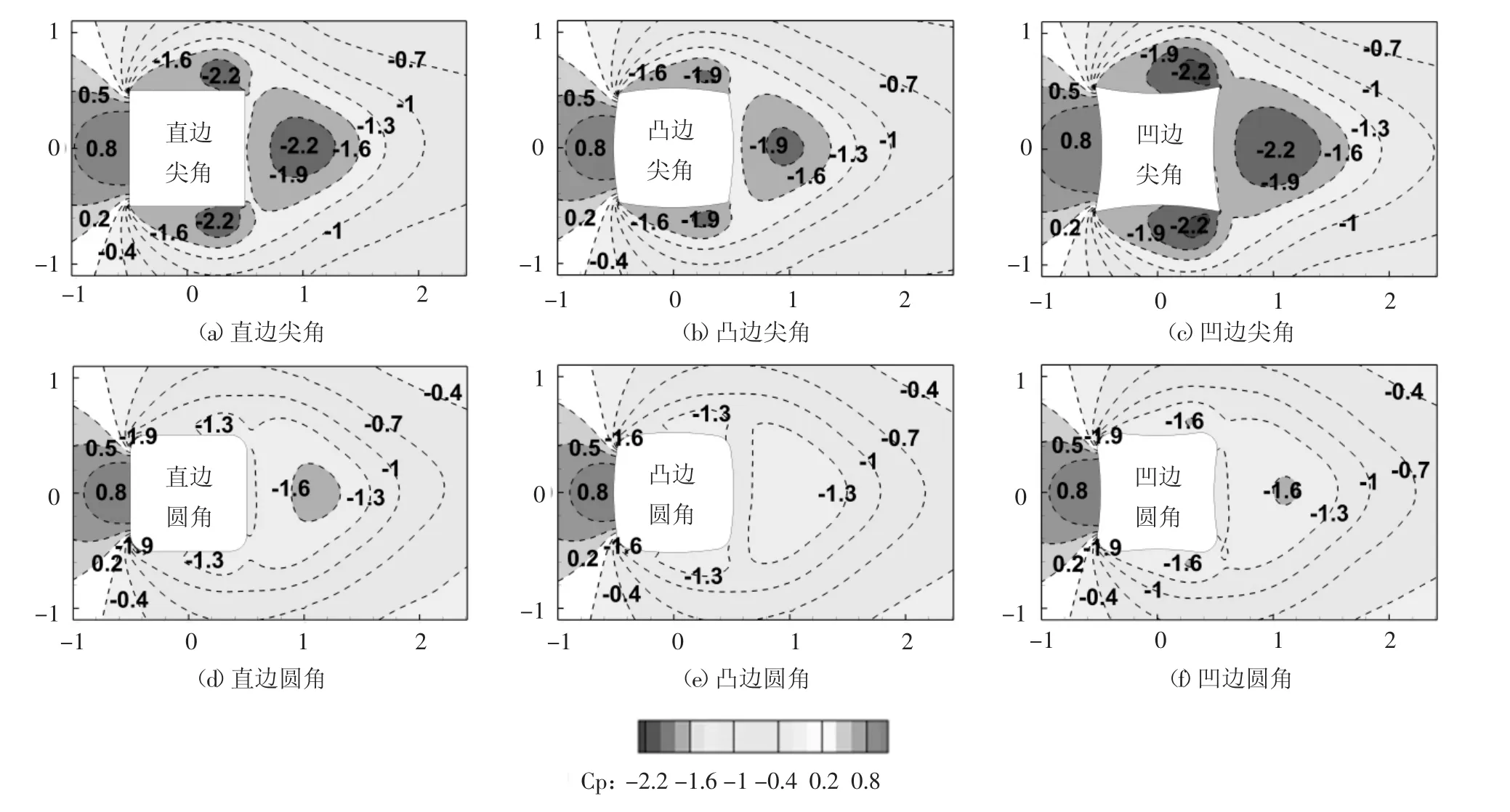
图8 角边形状对绕流场时均风压的影响Fig.8 Effect of corner and edge shape on time-averaged pressure fields

图9 角边形状对绕流场时均流线的影响Fig.9 Effect of corner and edge shape on time-averaged streamlines

4 边部曲率半径的影响

由上文结果可知，凸边修正和圆角措施的组合能最有效改善柱体的气动性能，本节以凸边圆角柱为研究对象，进一步探讨边部曲率半径对凸边圆角柱（角部率R/B=1/7）气动性能和流场特性的影响.

4.1 气动力系数和St数

图10给出了不同边部曲率半径下凸边圆角柱的气动力系数和斯托罗哈数.注意各柱体气动力系数均采用名义边长B无量纲化.

图10 边部曲率半径对气动力系数和斯托罗哈数的影响Fig.10 Effect of K/B on aerodynamic coefficients and Strouhal number

从图10（a）可见，随着边部曲率半径K/B的增大，柱体的平均阻力系数先减小后增大，在K/B=1.0时取得最小值，当曲率半径大于1.5时，K/B的改变对平均阻力系数的影响较小.与直边圆角柱和圆柱相比，不同边部曲率半径下凸边圆角柱的平均阻力系数均有不同程度的降低，即圆角措施和凸边修正的组合可以有效降低柱体的平均阻力系数.分析图10（d）可知，边部曲率半径对斯托罗哈数的影响与平均阻力系数的变化趋势基本相反，在K/B=1.0时斯托罗哈数最大，即涡脱频率最大.

由图10（b）可知，随着边部曲率半径的增大，柱体的脉动阻力系数经历了两次先减小再增大的变化，在K/B=1.0时第1次减小到极小值，在K/B=1.35时第1次增大到极大值，总的来看，在K/B=1.0时柱体的脉动阻力系数最小.分析图10（c）可得，边部曲率半径对脉动升力系数的影响与脉动阻力系数的变化趋势基本一致，在K/B=1.0时柱体脉动升力系数最小.

4.2 平均和脉动风压系数

图11分别为边部曲率半径K/B=0.564（圆柱）、1.0、1.35、2.5、∞（直边圆角柱）时凸边圆角柱的表面平均风压系数和脉动风压系数分布图.从图中可见，所有柱体中，当K/B=1.0时，柱体的平均和脉动风压系数均小于其余柱体.

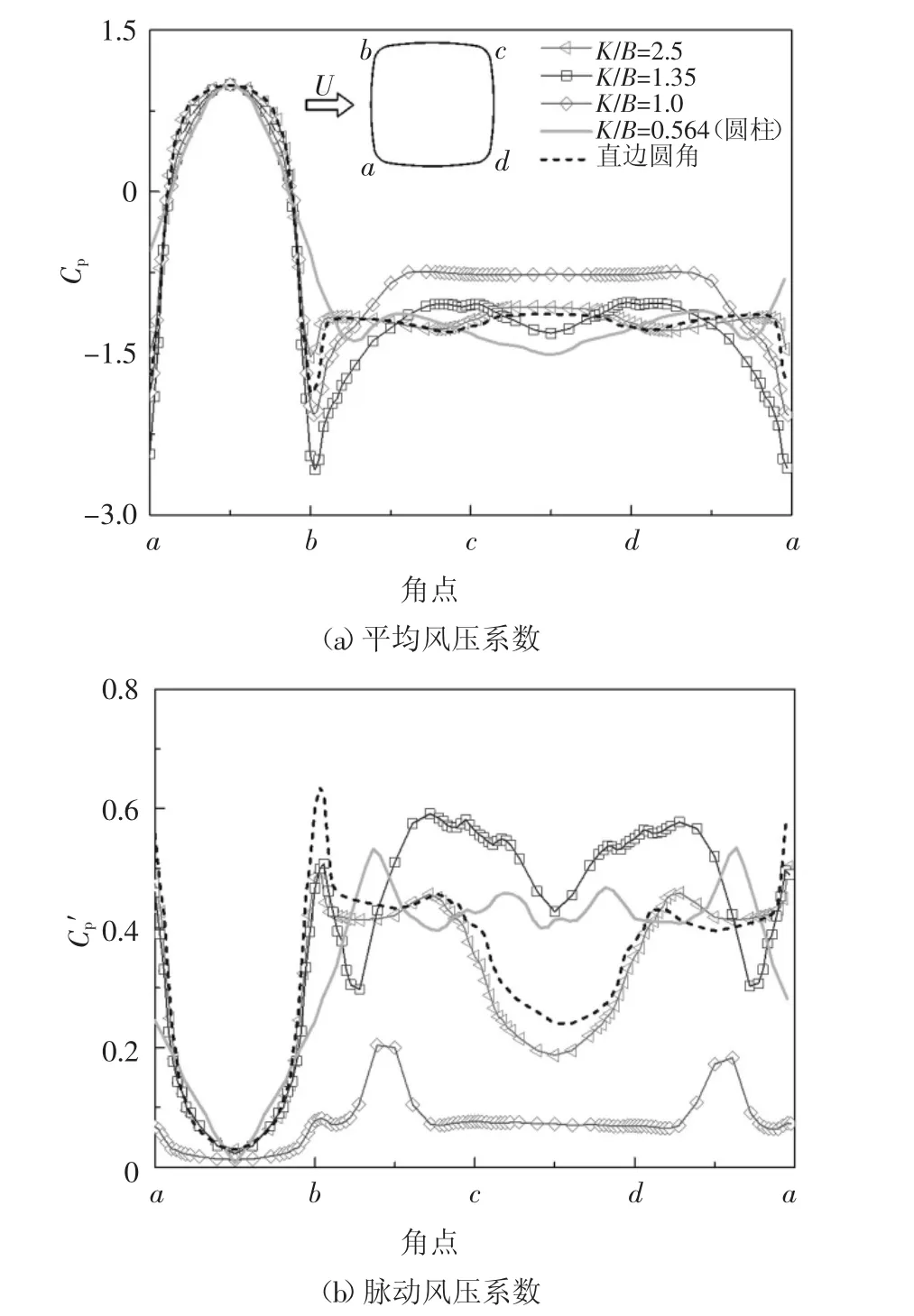
图11 边部曲率半径对表面风压系数的影响Fig.11 Effect of K/B on pressure coefficients

由图11（a）可知，迎风面上，各柱体平均风压系数基本一致；迎风面角点（a点和b点）至上、下侧边中点部分，圆柱和K/B=2.5的凸边圆角柱负压较小，K/B=1.35的柱体负压最大；上、下侧边中点至背风面，K/B=1.0的柱体平均风压系数最小，圆柱的负压最大，这导致K/B=1.0的柱体出现最小的平均阻力系数，圆柱平均阻力系数最大.值得注意的是，K/B=1.35凸边圆角柱的角部分离点附近的负压绝对值较大，从平均风速场（本文未给出）可知，这是由于该柱体气流分离点附近的局部风速更大造成的.

由图11（b）可知，整体上看，K/B=1.0时柱体的脉动风压系数在所有位置均小于其余柱体.迎风面上，除K/B=1.0的柱体外，其余柱体脉动风压系数基本一致；上、下两侧边处，圆柱和K/B=1.0的柱体在侧边中点处的脉动风压系数出现局部凸起，这可能跟后角点（c点和d点）的回流区有关；背风面c-d上，K/B=1.35的柱体脉动风压系数最大，这是该曲率半径下柱体背风面形成的两个回流区造成的.

总体上看，K/B=1.0下凸边圆角柱的平均和脉动风压系数普遍小于其余柱体，即该曲率半径下凸边修正和角部措施的组合效果最好.

4.3 平均风压场

图12给出了6种边部曲率半径下凸边圆角柱的时间平均风压场.总体上看，曲率半径K/B=1.0时，凸边圆角柱周边的负压强度最弱，负压极值最小.

由图12可见，边部曲率半径K/B＜1.0时，随着曲率半径的增大，柱体尾流强负压区强度逐渐减弱，直至强负压区消失；迎风面角点负压极值逐渐增大，K/B=1.0时柱体出现最大的角点负压.

K/B=1.35时，柱体迎风面角点和尾流区存在3个强负压区.由上文分析可知，K/B=1.35时，柱体出现较大的脉动气动力和脉动风压系数，这与平均风压场的分析结果相一致，从风压角度解释了该曲率下出现较大的平均阻力系数的原因.

随着K/B的继续增大，与K/B=1.0的柱体相比，各柱体上、下侧和尾流区负压强度均增强，迎风面角点处负压降低，这导致了平均阻力系数的增大和迎风面角点处平均风压系数的减小.

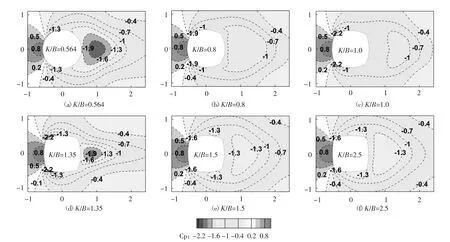
图12 边部曲率半径对绕流场时均风压的影响Fig.12 Effect of K/B on time-averaged pressure fields

4.4平均流态结构

图13给出6种边部曲率半径下凸边圆角柱绕流场的时间平均流线图.由图可见，不同边部曲率半径的柱体的平均流线有很大差异，尾流长度变化剧烈，K/B=1.0时的尾流长度最大，在两侧面背风面角点附近存在两个小回流区.

K/B＜1.0时，随着曲率半径的增大，气流初次分离点后移，柱体尾流长度逐渐增大，背风面角点附近的回流区范围逐渐减小，该回流区使得圆柱和K/B=1.0的柱体的脉动风压系数在两侧边出现局部凸起.

K/B=1.35时，柱体的尾流长度和宽度均达到最小值，背风面角点附近回流区消失，在背风面出现两个新的回流区，该曲率半径下出现柱体较大脉动气动力系数.

随着曲率半径的继续增大，与K/B=1.0的柱体相比，各柱体尾流长度逐渐减小，上、下侧边出现新的回流区.

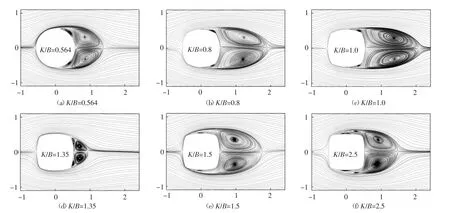
图13 边部曲率半径对绕流场时均流线的影响Fig.13 Effect of K/B on time-averaged streamlines

5 结论

以优化方柱气动外形为目的，采用大涡模拟方法，在雷诺数为2.2×104时，研究了16种类方柱的气动性能和流场特性，分析了角边形状和边部曲率半径对柱体气动性能的影响规律，并从流场角度探讨了形状修正对方柱气动性能的作用机理.主要结论如下：

1）对标准方柱的角、边形状的修正可明显改变其绕流场结构，会改善或劣化其气动性能；尖角柱体圆角化、直边柱体凸边化能显著降低气动力系数、表面风压系数和涡脱强度，从而改善了柱体的气动性能，且St数升高；直边柱体凹边化后会劣化气动性能.

2）不同角边形状的组合中，在凸边和圆角修正的组合下，柱体的平均阻力、脉动阻力和脉动升力以及负压区表面压力系数最小，体现出相对较好的气动性能；凸边和圆角的组合可导致分离剪切层更紧贴柱体壁面，上、下侧回流区范围变小，尾流回流区长度增大，涡脱强度减弱，气动力下降.

3）对于凸边圆角柱，其气动性能和流场特性对边部曲率半径非常敏感，研究发现存在一最优曲率半径，此时凸边圆角柱的平均和脉动气动力均达到最小值，负压区强度最弱，尾流回流区最长，涡脱强度最低.

本文研究表明，在风向角为0°时，K/B=1.0的凸边圆角柱具有较好的气动性能，但考虑到实际工程中来流风向是不确定的，今后应对不同风向角下K/B=1.0的凸边圆角柱绕流展开进一步研究.