基于颗粒流理论的颗粒材料振动流化特性研究
2020-06-03张谢东张志华
孙 仕 张谢东 张志华
(武汉理工大学交通学院1) 武汉 430063) (长江水利委员会长江科学院2) 武汉 430010)
0 引 言
静态摩擦和非弹性粒子间的碰撞形成了颗粒材料的一个重要特点——颗粒间的相互作用耗散[1].然而在振动过程中如果给颗粒材料提供足够的能量时,颗粒间耗散作用将得到弥补[2].当振动加速度a,超过某一临界值时,颗粒材料从固态到液态的转变叫振动流化(vibrational fluidization).例如,在垂直方向施加振动作用,当a大于1 g时,颗粒材料就会发生流化现象[3].
Richards等[4]提出了“动态流化”的概念,考虑了地震加速度在干燥土体颗粒的影响,当加速度施加在某一临界状态时,它改变了土体的状态导致增塑作用,在某种意义上讲,土体变成了一个各向异性的流体.这一概念同样被Fauve等[5-8]在试验研究中提到,他们假设引起流化的主要触发点是土体颗粒中的粒间惯性力作用.Taslagyan等[9]研究了振动强度的影响,结果表明流化主要取决于水平加速度,而不是垂直加速度,而且颗粒材料流化现象是通过在振动过程中剪切强度的损失反应出来的.在试验过程中发现,流化剪切带是一个狭窄的靠近剪切面的带状区域,但是在室内试验中很难得出其厚度.
为了克服室内试验确定流化剪切带厚度和深入了解颗粒材料流化特性的难题,本文基于离散元方法建立了三维颗粒流剪切振动流化数值模型.根据数值模型得到的宏观力学结果与室内试验值的吻合,更深入的分析在振动剪切过程中材料的力学特性.同时,根据测量局部体应变的变化规律,讨论流化剪切带在颗粒流模型中的分布情况.
1 室内剪切振动流化试验
室内剪切振动试验装置见图1[10],该装置根据传统直剪试验仪改装而成.剪切振动仪的测量装置包括两个传感器分别测量竖向位移和水平位移,两个载荷装置和两个单轴加速计分别加载和测量竖向和水平振动加速度.
此直剪测试方法遵循文献[11],在此基础上,当剪切试样达到残余强度时,增加水平振动强度.在水平振动过程中,下方剪切盒依然保持剪切状态.振动频率和强度调整到某一特定的大小进行土体试样的振动剪切试验.

图1 剪切振动流化试验装置
为了研究颗粒材料的振动流化现象,试验中运用直径为0.55 mm的玻璃珠作为颗粒材料.试验颗粒放置于60 mm×60 mm×32 mm(长(宽(高)的剪切盒中并振捣密实.竖向应力为23 kPa,下剪切盒剪切速率为0.61 mm/min,试样密度为1 566 kg/m3,孔隙比为0.692,上剪切盒振动频率为60 Hz、振幅为0.24 mm.
2 颗粒流模拟
2.1 模型建立
在数值模型中,根据室内试验的模型尺寸,颗粒分布的长度和高度由试验剪切盒实际尺寸确定.考虑到试验颗粒粒径极其细微,若按试样原尺寸建模,以0.55 mm粒径估算,颗粒总数将超过80万个,影响程序运行效率.为了尽可能提高模型的运算效率,数值模型中试样宽度取为8 mm,这一宽度取值满足模型最小长度尺寸Lmin与颗粒最大粒径dmax的比值大于10,即Lmin/dmax=8/0.55=14.5>10,此时模型计算得到的宏观力学性质具有较高的可靠性[12].
为了确保初始颗粒生成紧密,直接采用半径扩大法生成球颗粒,见图2.
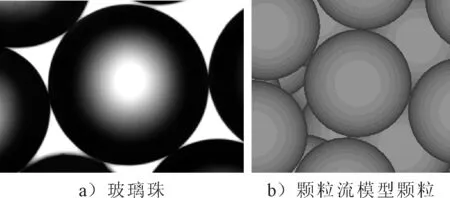
图2 室内试验显微镜下影像图
在生成颗粒分布的同时赋予相关的材料参数:摩擦系数、接触杨氏模量、法向与切向刚度比等.按照预设孔隙比确定颗粒的半径扩大系数,在达到指定孔隙比后执行应力初始化程序,释放由于半径扩大导致颗粒与颗粒间产生的过大接触力.在应力初始化完成后通过围压伺服控制系统对颗粒进行固结,固结完成后的试样和模型墙体分布见图3.
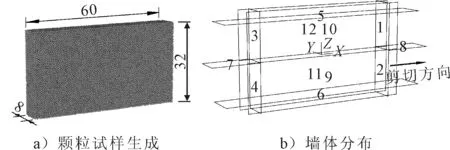
图3 颗粒试样生成和墙体分布图
墙1~4和墙9~12分别为左右和前后侧墙,控制试样剪切和振动;墙5为顶部伺服控制墙,在剪切过程中可以上下移动以维持不变的竖向应力;墙7和墙8为左右翼墙,在剪切过程中墙7会跟随下剪切盒移动,振动过程中墙8会跟随上剪切盒一起振动,其目的是为了防止颗粒溢出模型而影响试验结果.在试验过程中,下剪切盒剪切速率与室内试验保持一致,剪应力为
(1)
式中:F(4)为墙4上沿水平方向的不平衡力;L为试样长度,60 mm;Dh为剪切位移;W试样宽度,8 mm.
2.2 振动阶段模拟
为了模拟上剪切盒的简谐振动,将水平振动速度按时间等分的方法,将一个周期等分为m段相等的时间间隔,则每一段的时间间隔为
(2)
取墙体在施加振动阶段的运动方程满足正弦函数(或余弦函数),则墙体位移u为
u=Asin(ωt+φ)
(3)
式中:A为振幅;φ为初相位,这里取φ= 0;ω为角频率,ω=2πf.
对上式求导得墙体速度v为
v=2πfAcos(ωt)
(4)
将每一段ΔT的速度设为恒定,并取其速度为时段ΔT初始时刻速度,将式(2)代入式(4),则第i段ΔT的墙体速度为
(5)
上述推导实际上是将每一个周期分成多个微段,每一个微段的速度取其开始时刻的速度,图4为一个完整周期内上剪切盒的振动速度示意图.在同一个时间微段内,其速度保持为定值,曲线表示理论简谐振动,随着划分的微段数m增大,数值模拟振动将不断地逼近理论简谐振动.根据调试,当m≥15时可以较好的体现振动函数,实际数值模拟中m=21.
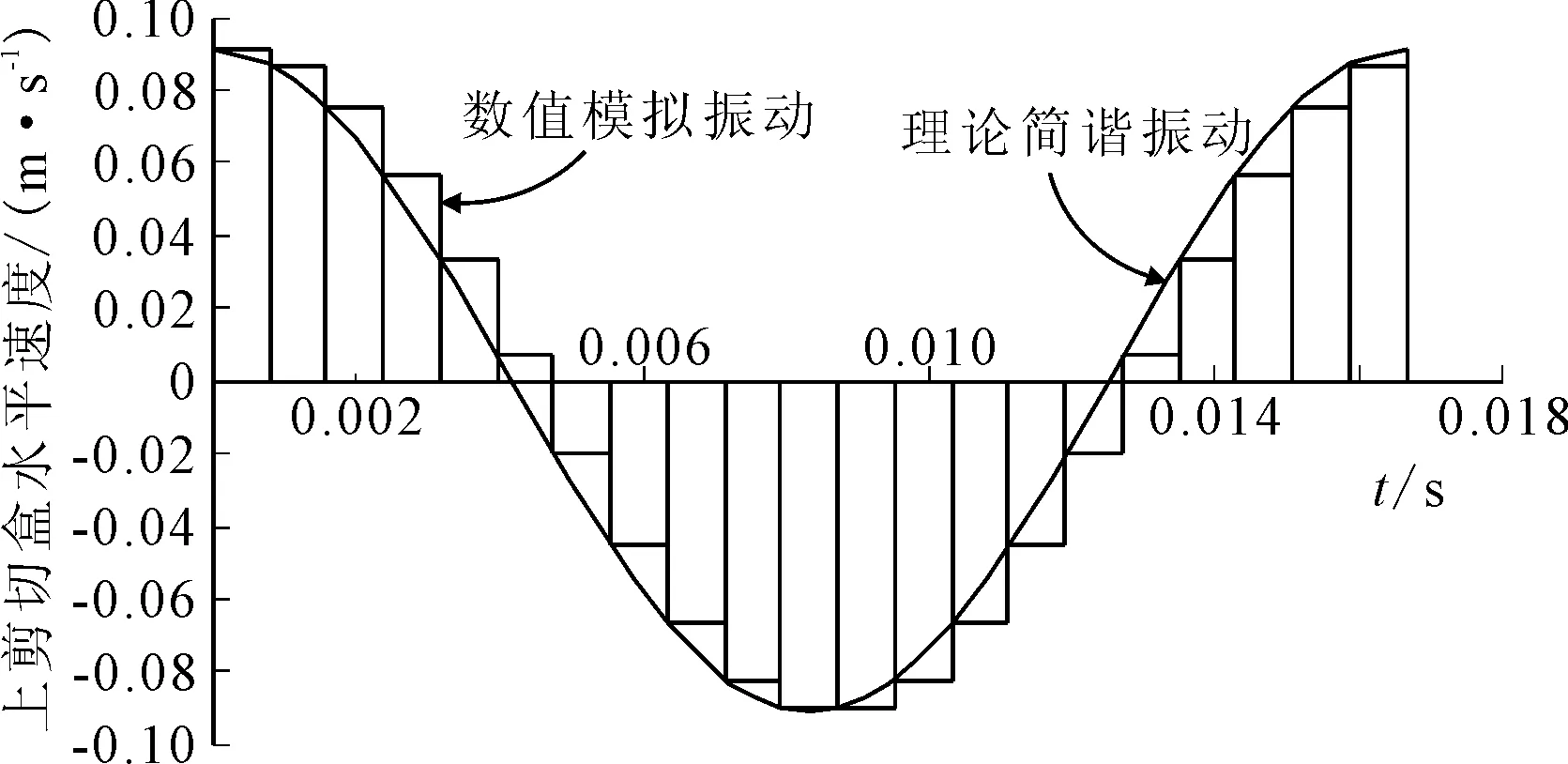
图4 上剪切盒在一个完整振动周期内的水平速度
当剪应变达到一定值时,按上述原理对上剪切盒施加振动速度.在振动过程中,墙5依然保持23 kPa的竖向应力.当振动结束时,上剪切盒固定不动,下剪切盒保持原有速率向右移动.
2.3 细观参数的标定
在颗粒流模拟中,与颗粒自身材料特性相关的细观参数和系统表现出来的宏观力学特性之间存在特定的联系.一般而言,模型的细观参数包括颗粒粒径、接触刚度与刚度比、颗粒摩擦系数、孔隙比、墙体刚度与摩擦系数等,对于任意一组给定的细观参数组合,均可在模型试验中获得唯一的宏观力学特性表征.对于颗粒的部分宏观力学性质可以通过试验得到,但由于材料各细观参数对整体宏观力学性质的影响存在较为显著的非线性,确定模型细观参数与对应的宏观性质之间的联系即模型的细观参数标定是一个关键而又复杂的过程,需要对各参数进行不断的取值和大量的试算.本次模型参数标定以振动前的室内试验结果为参照,通过一系列参数调整和数值试验,得到在竖向应力23 kPa下的玻璃珠试样各宏细观参数见表1.

表1 颗粒流模型中玻璃珠的细观参数
3 数值模拟结果
3.1 室内试验与数值试验结果对比
数值试验结果与室内试验结果见图5.由图5可知,数值试验曲线与室内试验曲线较为吻合,均表现出一致的变化特点:在振动前的剪切阶段,室内试验曲线在剪应变为0.02时达到峰值抗剪强度,随后开始软化并于剪应变为0.08时达到残余抗剪强度状态;在上剪切盒振动阶段,试样抗剪强度急剧下降甚至完全丧失,且呈现出明显的波动性;在振动后的剪切阶段,随着剪切继续进行,试样很快又再次达到峰值抗剪强度状态,且室内试验和数值试验均反映振动后的峰值抗剪强度大于振动前的峰值抗剪强度,这可能是因为在较高的振动强度下试样内部颗粒发生重组而变得更加密实,在一定程度上提高了抗剪强度.随后试样再次达到残余抗剪强度状态,且振动后的残余抗剪强度基本与振动前保持一致.
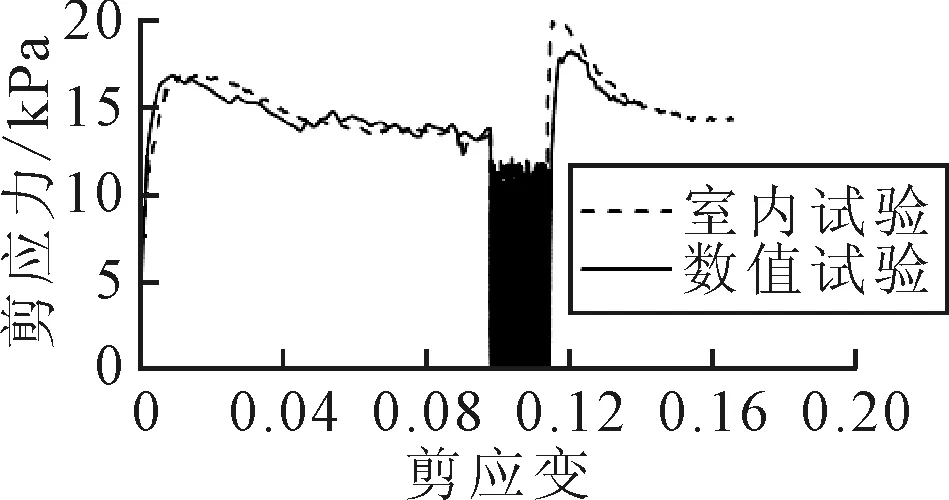
图5 数值试验与室内试验剪应力与剪应变关系曲线
数值试验和室内试验中模型顶部加载板竖向位移与剪应变关系曲线见图6.由图6可知,数值试验结果均与室内试验偏差较大,但整体趋势一致.在振动前的剪切阶段,室内试验竖向位移在剪切一段时间后开始上升并逐渐稳定于0.3 mm,数值试验竖向位移则在剪切开始阶段经历微弱的下降后随即上升至0.65 mm,这反映了试样表现出持续的剪胀作用;进入振动阶段,室内试验竖向位移急剧下降至-0.55 mm,而数值试验竖向位移则下降至0.2 mm,下降幅度小于室内试验,在这一过程中试样发生剪缩作用;振动结束后试样竖向位移再次上升,发生剪胀作用.
分析数值试验与室内试验存在偏差的原因可能有以下几点:①模型的建模误差.由于模型中在试样宽度方向的取值较小,试样在前后墙体的约束作用下可能更多地表现出沿高度方向运动的趋势,从而导致试样竖向剪胀较大[13];②试样的初始密实程度存在偏差.室内试验中的试样在固结过程很难使颗粒达到均匀的致密状态.在剪切开始后,颗粒相互挤压,沿水平向运动填补孔隙,因此并没有表现出明显的剪胀剪缩性,竖向位移在剪应变达到0.02之前几乎没有变化.而在模型试验中,经过应力初始化和伺服固结后试样已经较为密实,相比室内试验固结完成后的试样,其孔隙比更小且内部应力分布更为均匀,在剪切开始后剪胀性表现更为明显;③可能存在的颗粒破碎情况.在室内试验中,即使23 kPa的竖向应力取值不大,在试样剪切至较大应变时或是在上剪切盒的剧烈振动过程中也很难保证颗粒不会发生破碎.在数值试验中颗粒是理想的刚性体,在接触力较大时,颗粒之间只会发生少量重叠而不会破碎;此外,也不能排除室内试验颗粒摩擦分布不均产生的影响.
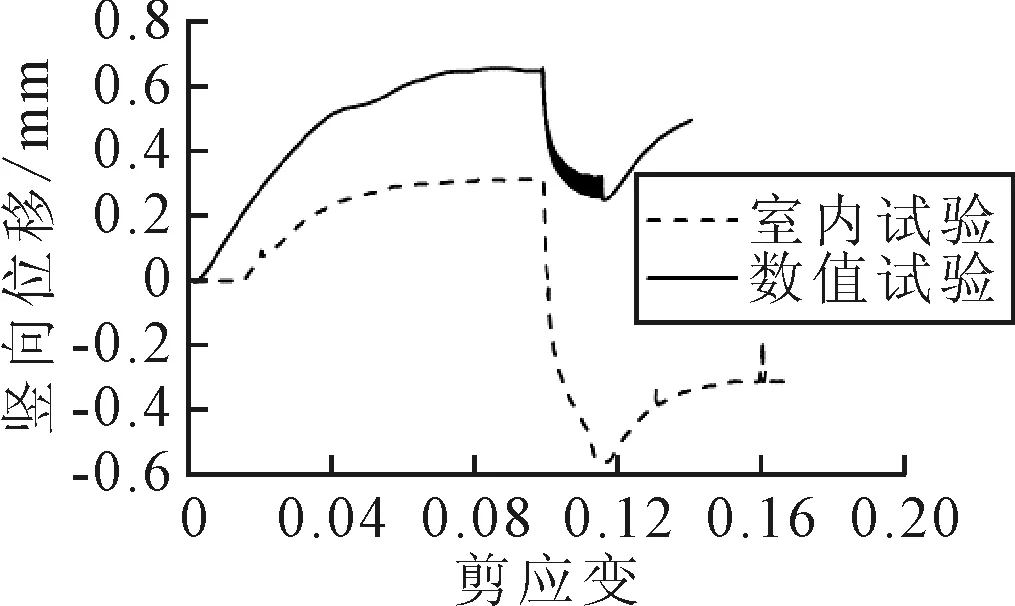
图6 数值试验与室内试验加载板竖向位移与剪应变关系曲线
3.2 剪切带厚度确定
为了测定流化剪切带的厚度,本文通过建立监测模型来记录剪切盒在剪切过程中体应变分布.监测模型由多个虚拟测量球组成,在本文的数值模型中,沿剪切盒自上而下共布置了7行直径相同的测量球(直径为2 mm),每行10个,共70个.测量球之间两两相切且按等间距排列.模型内的测量球分布见图7a),根据测量球监测局部体应变与振动前剪应变的变化规律,将整个模型分为五个区域,沿试样高度自上而下分别I,II,III,II’和I’.各区域内平均体应变随剪应变的变化规律见图7b),体应变分布在模型内部各区域具有明显差异.在剪切过程中,位于区域I内的颗粒体体应变变化较小,表明该区域颗粒体未发生剪切现象;位于区域II内的颗粒体体应变随着剪应变的增大而增大,颗粒体发生剪胀现象;位于区域III内的颗粒体,其体应变随着剪应变的增大而增大,且增值明显大于位于区域II内颗粒体体应变增值.因此可以推断出区域III为模型试样剪切带分布区域,且剪切带厚度为4 mm,见图7a).
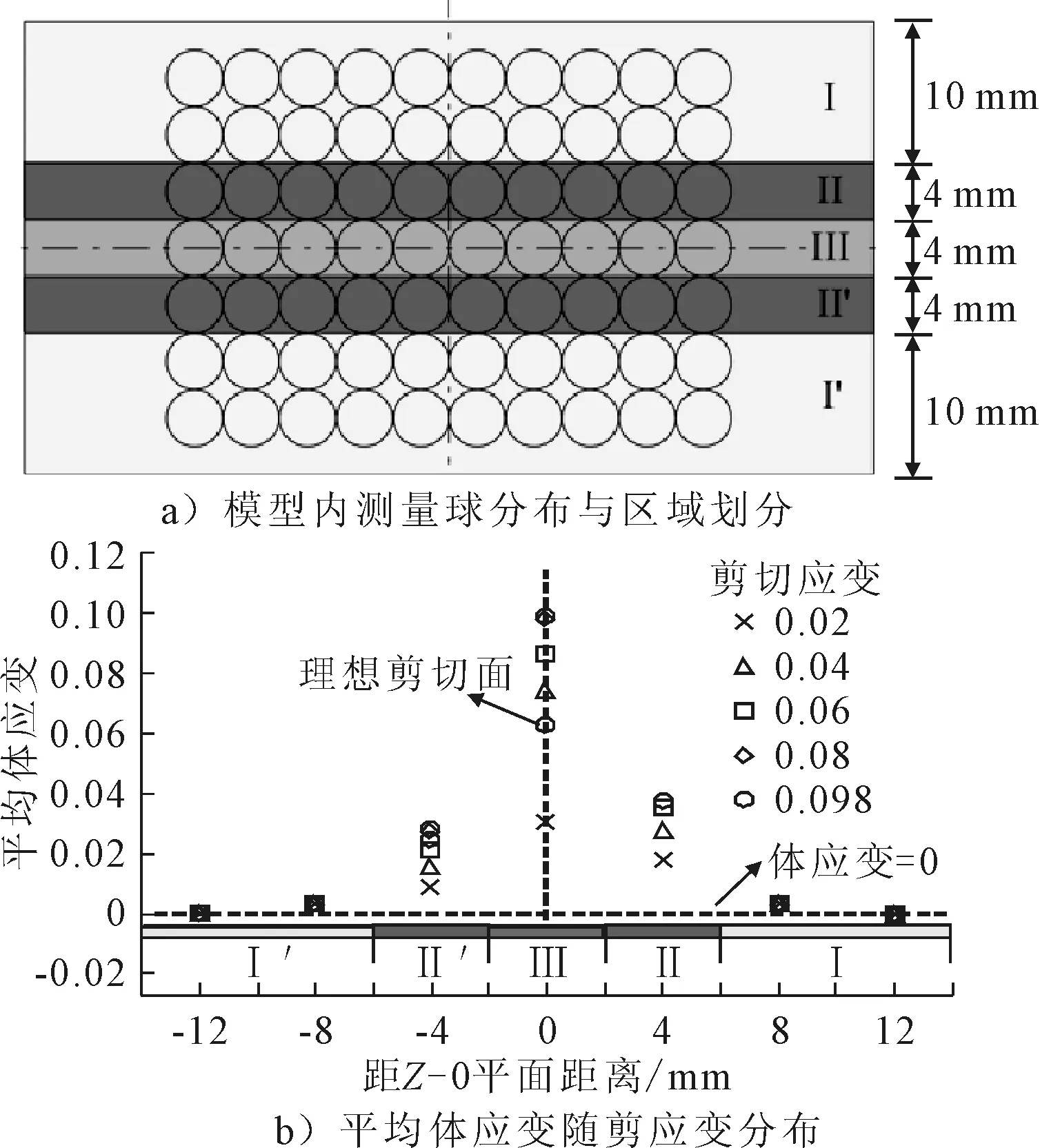
图7 模型内测量球分布与区域划分和平均体应变随剪应变分布
在剪切过程中,局部体应变分布可以描述试样在局部区域内的剪胀与剪缩特性,是反映应变局部化现象的一大特征参数.这里重点关注位于上剪切盒的三个主要振动区域(I,II和III)内的平均体应变演化与剪应变的关系,见图8.在振动剪切阶段,三个区域平均体应变演化具有显著的差异,区域I内平均体应变呈现微弱的下降,这反映了在振动剪切过程中该区域受剪切作用的影响较小,区域III内则出现急剧的下降,意味着在这一区域内的颗粒相互作用最为显著,颗粒在振动过程中不断改变其空间位置而反复重组,产生流化现象.区域II平均体应变则在短暂的降低后在小范围内波动,这是因为该区域位于区域III上方,受该流化剪切带内的颗粒影响,交界面的部分颗粒也会发生流化,这一现象也反映了流化剪切带与非剪切区域之间并没有明确的界限面,区域II可以认为是两者的过渡区域.综上所述,在振动剪切过程中模型内颗粒体局部体应变均减小,表明颗粒材料逐渐密实,导致振动结束后颗粒材料的抗剪强度增大,且峰值抗剪强度大于初始峰值强度.
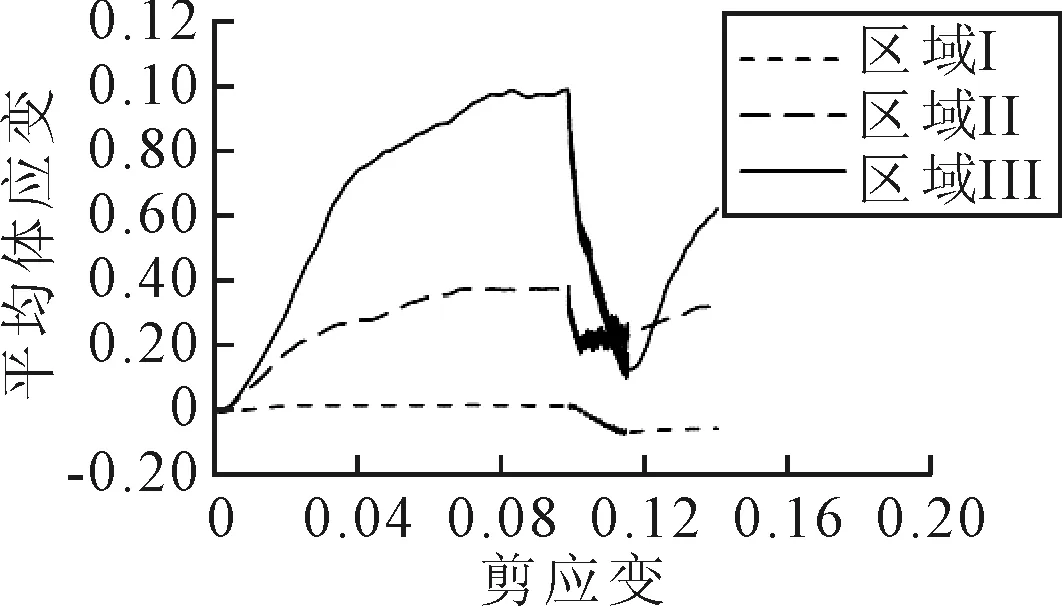
图8 上剪切盒不同区域内平均体应变与剪应变关系曲线
4 结 论
1) 室内试验和数值试验结果均显示在振动过程中,试样的抗剪强度会减小到一定值,出现流化现象.振动结束时,由于模型内部颗粒发生流化重组后试样整体变得更为紧密,导致试样表现出比振动前更高的抗剪强度.
2) 根据体应变的变化规律将模型划分为多个区域.流化剪切带出现在理想剪切面附近的狭小区域,其内部颗粒相互作用最为显著,应变局部化现象明显,流化剪切带厚度为4 mm.
3) 剪切振动过程中,颗粒材料抗剪强度、模型顶部墙体竖向位移以及局部体应变均减小,表明颗粒材料在一定水平振动加速度条件下进行振动剪切,具有流化特性.
