粉末燃料的沉降速度和最小流化速度分析①
2019-11-15霍东兴何俊卿马娟娟
霍东兴,何俊卿,马娟娟
(1.中国航天科技集团有限公司四院四十一所,西安 710025;2.中国航天科技集团有限公司四院四十七所,西安 710025)
0 引言
在航天领域,粉末发动机具有能量密度高、比冲高、可重复启动等优势,在导弹武器、空天运输等领域具有广阔的应用前景[1-5]。粉末燃料作为航天动力装置的能量源,其流量必须进行精确控制,才能够对发动机推力进行精确控制,研制体积小、重量轻、流量精确可控的粉末输送装置是航天动力系统的基本要求。粉末既具有固体的性质,又具有流体的性质,气力输送是工业上大量应用的一种粉末输送方式,即通过气体对粉末进行流化,由气体携带粉末实现粉末物质的输送。
铝、镁、硼等物质具有热值高、工艺性良好等特点,是粉末燃料的优选材料,它们的密度范围为1.7~2.7 g/cm3,粉末燃料粒度应同时满足高效燃烧和气力输送的需要。本文研究的粉末燃料粒度为20~300 μm;颗粒密度为2.5 g/cm3,堆积密度为1.3 g/cm3,孔隙率为0.48;球形度为0.85;流化气为空气,并假设在高温高压流化过程中粉末燃料的颗粒密度、粒径不发生变化。
1 粉末输送原理
在总结国内外研究的基础上,文献[5]提出的气压驱动活塞式输送装置见图1。流化气沿径向进入锥形的流化区,将粉末流化并经过球阀输出;驱动气形成一定的压强作用在活塞上,推动粉末不断进入流化区。通过控制驱动气压强、流化气流量以及球阀的面积实现对粉末流量的控制。可看出,这种输送装置和工业上大量应用的粉末流化床存在如下差异:
(1)流化区范围不同。本装置的流化区仅仅作用于粉末出口区域的很小范围内,而常规流化床的流化区作用于整个物料。
(2)粉末流动方向不同。本装置的粉末流向是远离物料的方向,流动过程中几乎没有受到固定床的影响,而普通流化床总是全局流化,并穿过“固定床”,必须克服重力作用。
(3)流化过程受到粉末压实程度的影响。常规的流化床,粉末处于自由堆积状态,堆积密度较小;而本装置粉末的压实程度主要取决于活塞的驱动压强,不同的压实程度会影响颗粒之间的作用力,从而影响流化过程。

图1 粉末输送装置结构示意图
粉末流化的原理是以气体的动量克服粉末重力、粉末之间的摩擦力、范德华力、静电力等,使粉末随着流化气一起流动,从而实现粉末的输送。尽管本装置和常规流化床有一定差异,但其流化原理相似。1884年,英国科学家Isaac Roberts在研究粮仓底面的压强时发现了粮仓效应[6],即当粮食堆积高度约大于2倍底面直径后,粮仓底面所受的压强不随粮食的增加而增加。由此可知,当活塞距流化区距离较远时,流化区内粉末所受的压强并不随驱动气压强的增大而增加。因此,粉末压实程度对流化过程,特别是流化启动过程的影响是很有限的。对本文研究的粉末输送装置,正常工作时的固气比范围约为10~120,对应的空隙率为0.97~0.71,与常规的气力输送没有差异,因而可用经验公式进行计算分析。
鉴于该粉末输送装置还处于概念设计阶段,分析粉末燃料的沉降速度和最小流化速度,能够为流化参数的设计提供一定参考。
2 沉降速度
置于无限大静止气体介质中的一个颗粒,在重力作用下会向下降落,受到的力包括重力、浮力和气流曳力。由牛顿第二定律得到:
(1)
随着气流速度ug的增加,曳力不断增大。到达某个速度ut时,作用在颗粒上的重力、浮力和曳力之和为零,颗粒以该速度匀速下落,这个速度为颗粒的终端沉降速度[7]。
对终端沉降速度可以这样理解:假定单颗粒静止在一个筛网上,气流穿过筛网对颗粒产生向上的作用力。当气流速度低于终端沉降速度时,颗粒将静止在筛网上不动;当气流速度等于终端沉降速度时,颗粒将漂浮在空中,不需要筛网的支撑而静止不动;当气流速度大于终端沉降速度时,颗粒将以绝对速度(ug-ut)随气流一起运动。
由式(1)当dup/dt=0时,可求得颗粒的终端沉降速度:
(2)
(3)
其中,ν为运动粘度,m2/s;常用的还有动力粘度μ,Pa·s。二者关系为ν=μ/ρg。
流化气为空气时,其粘度和温度的关系为μg=1.46×10-6×T1.504/(T+120),T为绝对温度。流化气的压强、密度、温度遵守理想气体方程。
阿基米德准则数Ar为
(4)
CD和雷诺数Re有关,具体为[7]:(1)当Re≤1时,CD=24/Re;(2)当700 (5) 对于一般的气力输送,颗粒直径、颗粒密度、流化气密度、流化气粘度可以得到。由式(4)可得到Ar,然后由式(5)得到Ret。最后,根据雷诺数的定义式,得到沉降速度ut。 对粉末燃料的沉降速度计算结果见图2。沉降速度随着颗粒直径的增大而增大,随着流化气温度的升高而减小,随着流化气压强的升高而降低。压强越高,温度对沉降速度的影响越弱。从图2(b)可见,25 ℃、0.1 MPa下的沉降速度最大为2.5 m/s,表明流化区域内流化气的速度至少需要2.5 m/s,才能实现粉末燃料的气力输送。 (a)0.026 5 MPa (b)0.1 MPa (c)1.0 MPa (d)3.0 MPa 将粉末颗粒置于一个敞口容器中,从底部均匀地加入气体,随着气体流量的增加,颗粒之间的结合力逐渐减弱。当气体对颗粒的曳力刚好等于颗粒的重力减去气体对它的浮力时,颗粒就像没有重量一样,可以横向移动。刚好使床层阻力不再增加的流化气速度称为最小流化速度。试验中,一般用沿床层厚度的气体压降来表征床层阻力,当通过床层的气体压降不再随着流化气的速度改变时,床层就处于临界流化状态,此时的气体速度叫做最小流化速度,也叫临界流化速度。针对特定的粉末颗粒和流化气,通过大量的流化试验获得一系列临界流化条件下的颗粒的临界雷诺数,并计算阿基米德数Ar,通过数据拟合获得类似于式(5)的关系式,这样就能够预测其他流化参数下的最小流化速度。 最小流化速度是针对有限空间内的颗粒群,而非单个颗粒,而沉降速度是针对无限大空间内的单个颗粒。实际流化床中,粉末颗粒均以颗粒群的形式进行输送,颗粒与颗粒之间、颗粒与壁面之间的碰撞,流化床沿横向的颗粒浓度不均匀性等均影响颗粒速度。因此,最小流化速度更能反映气力输送的实际情况。有研究者将其定义为床层孔隙率ε由0.4向大于0.4过渡时的速度[8],大于临界速度且小于沉降速度就是流态化速度。此时,床层孔隙率ε=0.55~0.75。而沉降速度下,床层孔隙率ε=1。 几十年来,各国学者对粉末气力输送问题进行了大量的理论研究和实验研究[9-14]。由于颗粒物料密度、粒径的宽广性,流化条件的多样性,尽管已经提出了上百个最小流化速度的经验公式,但还没有一个普适方法。根据本文粉末燃料的密度、粒度,选择了4种经验公式,它们均考虑了流化温度和压强的影响,可满足本文的分析需要,见表1。 从图3(a)可见,在常温常压下,随着粒度的增大,最小流化速度增大。除陈振东模型预示结果明显较高外,其余3个模型非常接近,主要原因是各作者的试验条件存在差异。同时,由于流化过程存在颗粒与颗粒、颗粒与壁面之间的碰撞以及动量的传递,使得最小流化速度比沉降速度小得多。 Nakamura、陈振东等用试验的方法研究了高温条件下的最小流化速度,提出了相应的经验公式,见表1。Fletcher研究了大量试验数据,提出了预示高温下的umf的方法[14]: (1)对于某个直径的颗粒,先选择一个温度,计算该参考温度下的umf; (2)然后,由kf=umf·T0.27计算kf; (3)根据各温度下kf相等,计算另一温度下umf。 图4为两种方法的计算结果。可看出,Nakamura和Fletcher的计算结果较为吻合。随着流化气温度的升高,最小流化速度减小。当粉末粒径小于100 μm时,温度对其最小流化速度的影响非常小,粒径大于300 μm时,温度的影响较为显著。 表1 计算umf的Remf-Ar经验关系式 (a)常温常压(298 K,0.1 MPa) (b)高温高压(600 K,1.0 MPa) (a)Fletcher(kf修正),0.1 MPa (b)Nakamura,0.1 MPa 常温下流化气压强对最小流化速度的影响规律见图5。可看出,Nakamura和Chitester的计算结果较为吻合。随着流化气压强的升高,最小流化速度减小。当粉末粒径小于100 μm时,压强对其最小流化速度的影响非常小,粒径大于300 μm时,压强的影响较为显著。 从图3(b)可见,在600 K、1.0 MPa流化工况下,各经验公式的计算结果趋势一致,即随着粒径的增大,最小流化速度升高。在高温高压下,粉末燃料的最小流化速度相比常温常压下明显降低。 (a)Nakamura,298 K (b)Chitester,298 K (1)沉降速度随着颗粒直径的增大而增大,随着流化气温度的升高而减小,随着流化气压强的升高而降低;压强越高,温度对沉降速度的影响越弱。文中的粉末燃料在常温常压下的沉降速度最大为2.5 m/s。 (2)最小流化速度与流化床的尺寸、颗粒直径分布、颗粒密度以及流化气的温度和压强有较大关系,不同试验条件所得到的经验公式不尽相同,但所得的影响规律一致:流化气温度和压强对粉末颗粒的最小流化速度的影响规律是相同的,即随着温度和压强的升高,最小流化速度降低,小于100 μm的颗粒,最小流化速度基本不随温度和压强的变化而变化;颗粒直径越大,最小流化速度越大。因此,应按照最大粒径的流化需求来设计流化气速度,对本文研究的粉末燃料流化问题,流化速度至少需要0.1 m/s。 (3)在相同条件下,由于颗粒与颗粒之间、颗粒与壁面之间的碰撞,最小流化速度比沉降速度小得多,实现粉末的流化和输送,按照沉降速度设计流化气的速度,自然能够满足最小流化速度的需求。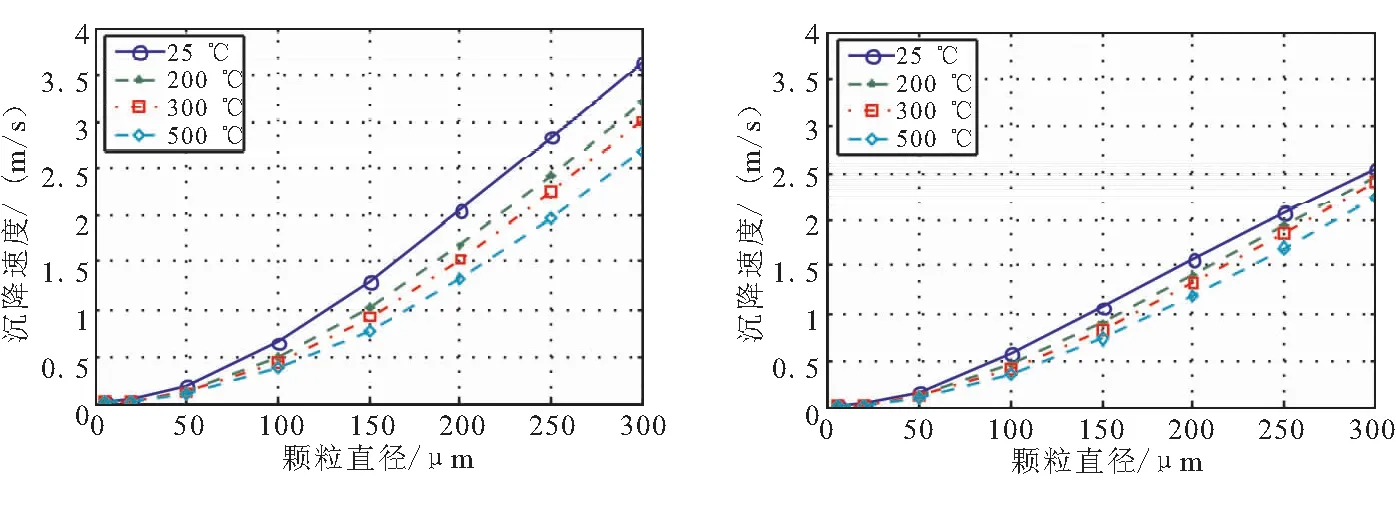

3 最小流化速度
3.1 常温常压下的最小流化速度
3.2 温度对最小流化速度的影响



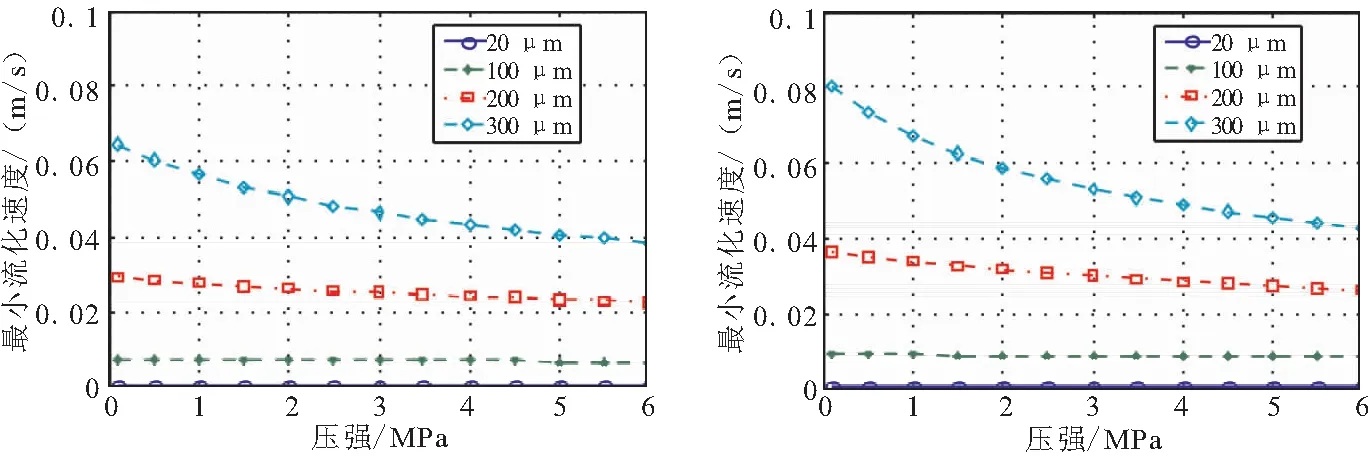
3.3 压强对最小流化速度的影响
3.4 高温高压下的最小流化速度
4 结论
