循环载荷下含裂纹加筋板承载力性能研究*

冯 帆 杨 平 胡 康 李 闯

(武汉理工大学交通学院 武汉 430063)

0 引 言

船舶航行时会同时受到多种载荷的作用，此时甲板和船底板会承受同时来自纵向压缩(拉伸)力和货物设备重量,以及水压力的作用.船体结构在海浪的往复作用下容易萌生出裂纹，对船舶结构的极限承载性能具有明显的削弱作用.加筋板具有结构简单，易于焊接制造等特点，是船体结构的主要组成部分，因此,考虑在纵向循环载荷和侧向压力共同作用下的加筋板极限承载性能具有实际意义.

目前国内外学者对加筋板在一次加载情况下的极限强度进行了比较充分的研究，而对循环加载下加筋板结构的承载性能研究则较少.Yao等[1]采用数值模拟的方法，通过改变循环载荷幅值、循环次数和板厚来探讨不同因素对板崩溃和屈曲行为的影响，计算结果表明板在循环载荷下的弹塑性变形性能与载荷的循环加载路径密切相关.Paik等[2-3]通过实验和有限元法，分析了含裂纹钢板在轴向压缩载荷下的极限强度，并给出了相应的经验公式，同时还研究了非线性分布侧向载荷对船体板材极限强度的影响.胡勇等[4]利用有限元法，研究了具有初始缺陷和裂纹损伤的板和加筋板在组合载荷作用下的极限承载性能，分析了各种参数和各种损伤对极限承载性能的影响，计算结果表明纵向拉伸极限强度会随横向压力的大小发生线性变化，并提供了相应的回归计算公式，具有一定的实用价值.李政杰等[5]采用非线性有限元法，对四种加筋板在不同载荷工况下的极限强度进行了计算，计算结果表明侧向载荷会大幅降低加筋板结构的极限强度，加筋板的崩溃形式也可能会发生变化.张婧[6]采用数值模拟对同时承受轴向和侧向压力作用的加筋板结构进行了分析计算，并将计算结果与模型试验进行对照，发现在联合载荷的作用下加筋板变形更大且塑性分布区域更广.任慧龙等[7]认为船舶结构在循环载荷下的极限承载能力与载荷的加载方式、载荷大小、载荷幅值,以及循环次数等因素都有关系，并基于递增塑性理论导出了循环弯矩下船体梁总纵极限强度的分析方法，并编写了相应的计算程序.崔虎威等[8]通过非线性有限元法，对承受复合受力作用的板和加筋板进行了计算，探讨了单元尺寸，边界条件，初始变形等多种因素对船舶基本结构的影响.

本文运用非线性有限元法，针对加筋板同时承受纵向循环载荷和侧向压力的情况，探讨了裂纹的分布位置、裂纹长度、侧向载荷大小和加筋板面板板厚对加筋板极限承载性能的影响.

1 有限元模型及相关理论

1.1 船体板的结构尺寸和材料属性

加筋板的结构尺寸和材料属性取自Zhang等[9]的算例，使用理想弹塑性材料建立模型，不考虑材料的强化作用，屈服准则设为von Mises屈服准则，屈服应力σy=313.6 MPa，弹性模量E=205 800 MPa，泊松比0.3，详细参数见表1.本文计算模型采取的是筋条与其带板组合而成的筋板组合模型，并以此组合模型为模型范围进行系列数值研究，其中筋条均为扁钢；根据裂纹分布的位置将模型分为图1的四类，所有裂纹的宽度均为3 mm，在裂纹的尖端用直径为3 mm的半圆来模拟.

表1 加筋板的几何参数

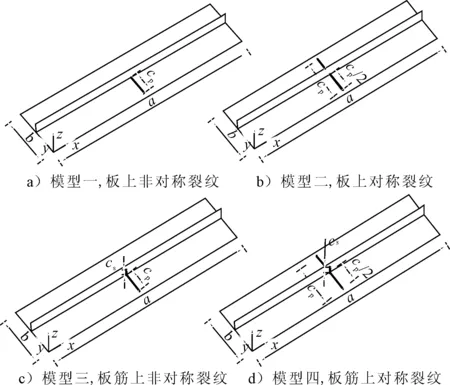
图1 加筋板裂纹分布图

1.2 加筋板的网格划分与边界条件

利用有限元软件Abaqus来进行含裂纹加筋板在不同情形下的极限承载力性能研究，采用S4R单元建立加筋板模型.已有的研究表明，网格的大小会影响裂纹尖端处的应力分布，但对加筋板整体的承载能力影响很小，因此,在裂纹尖端和附近区域细分网格，具体分布见图2.加筋板受到纵向或横向强构件的支撑作用，考虑到本文选取的一弯一跨模型，加载边取为简支条件并设置以中点为耦合点的刚域 ，非加载边则约束对应的角位移并设置沿y方向的耦合.

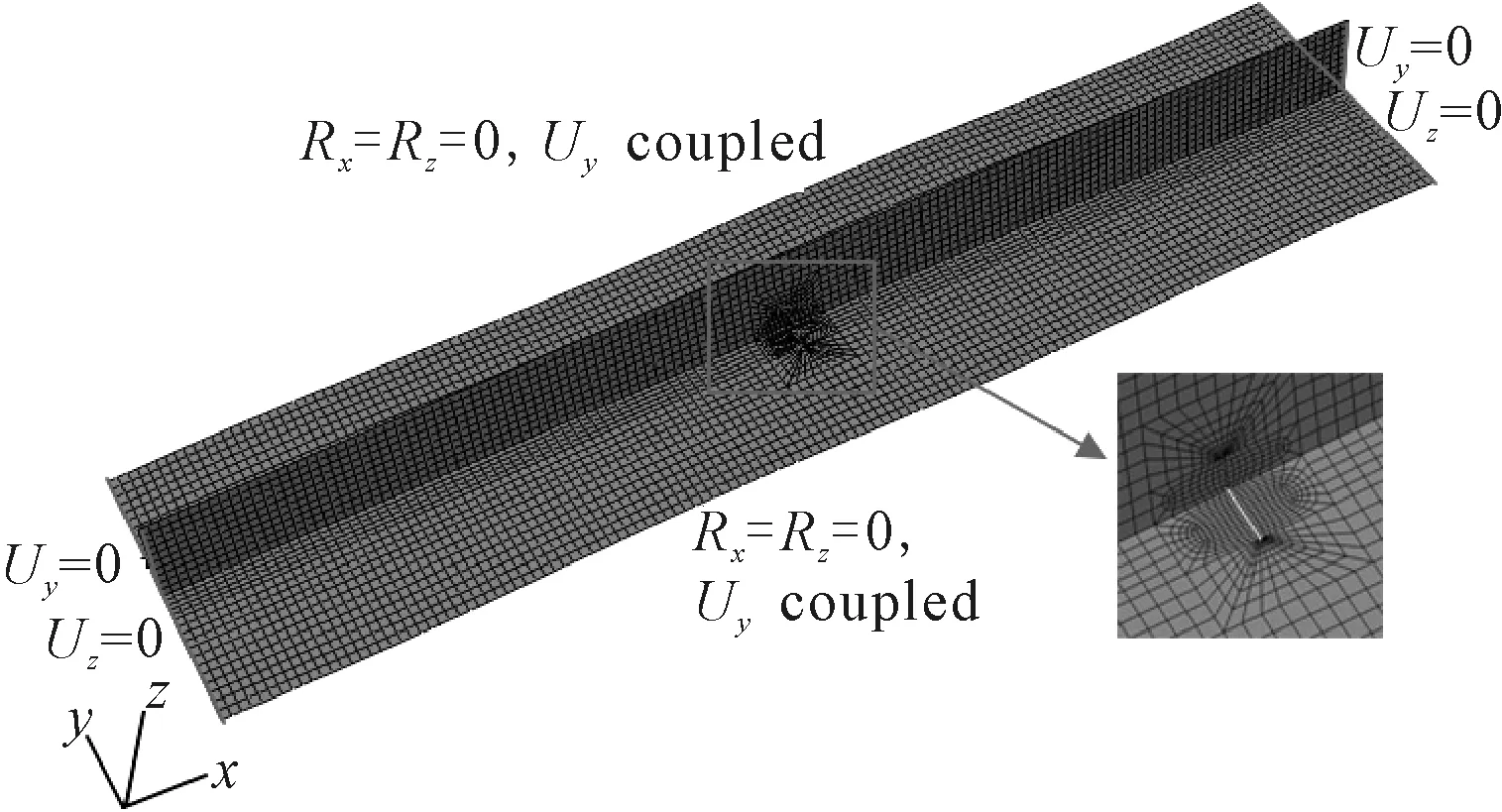
图2 加筋板网格划分与约束条件

1.3 加筋板的初始缺陷和载荷施加

船舶结构由板以及骨材焊接而成，在加工和焊接过程中加筋板不可避免地会产生初始缺陷，主要分为初始变形和焊接残余应力.现有的研究表明初始挠度对加筋板结构的极限承载能力有较大影响，而焊接残余应力的影响则较小，因此本文在进行有限元计算时只考虑初始挠度的影响.加筋板的初始变形一般由板格的初始变形、加强筋的初始变形和加强筋的侧倾变形组成，分别为

1) 板格的初始变形

(1)

2) 加强筋的初始变形

(2)

3) 加强筋的侧倾变形

(3)

式中：a为板长；b为板宽；hw为加强筋的高度；A0，B0，C0分别为三种初始变形的幅值；m为纵向屈曲半波数.考虑到直接将屈曲模态以指定幅值施加到计算模型会与真实情况存在差距，本文通过编写自定义扩展程序，直接偏移单元节点的坐标来实现初始变形的形状，这样会更符合实际情况.

对于甲板和船底板，会同时承受面内的纵向载荷以及面外的侧向载荷，侧向载荷的方向与海水作用于船底板的方向一致；在加筋板的纵向，采用位移控制的方式来施加循环载荷，在两条短边处施加大小相等方向相反的位移，写出不同时刻对应的载荷大小，建立多个计算载荷步；在加筋板的侧向，施加恒定均匀分布的面载荷，面载荷的大小取自文献[10].在进行非线性有限元计算时，均保证载荷的加载路径相同，即每一步的卸载点与该计算步的循环增量相同.

2 循环载荷下含裂纹加筋板的有限元计算

2.1 有限元法的验证

为了对船舶和海洋平台结构进行极限状态设计和强度评估，Paik运用非线性有限元法和半解析法对双向压缩和侧向压力联合作用下的板以及加筋板结构进行了极限强度计算.本文在相同的条件下选取对应的加筋板模型进行计算，并将得到的结果与Paik的计算结果进行对比，具体的计算结果参见表2.由对比可知，计算结果与文献的结果能够较好地吻合，验证了本文非线性有限元方法计算的准确性.

表2 有限元结算结果与文献结果比较

2.2 板厚对加筋板承载性能的影响

选取加筋板模型四来研究板厚对含裂纹加筋板承载能力的影响，其中面板上的裂纹长度cp/b取为0.2，加强筋的板厚均为25 mm，加强筋上的裂纹长度cs/hw=0.2.

图3为模型四承载力随板厚变化曲线，由图3可知，随着板厚的增加，加筋板的承载能力会显著的提高，原因是随着板厚增加，加筋板上的高应力区域明显增加，更多结构参与了抵抗变形的作用.虽然在同样的循环次数下，厚板的承载能力优于薄板，但随着循环次数的增加，厚板的承载能力会下降得更快，薄板的承载能力也在下降，但下降的速度越来越缓慢，原因是随着板厚的增加，循环载荷造成的累计塑性变形也会更严重，这导致了其承载能力的下降速度加快.

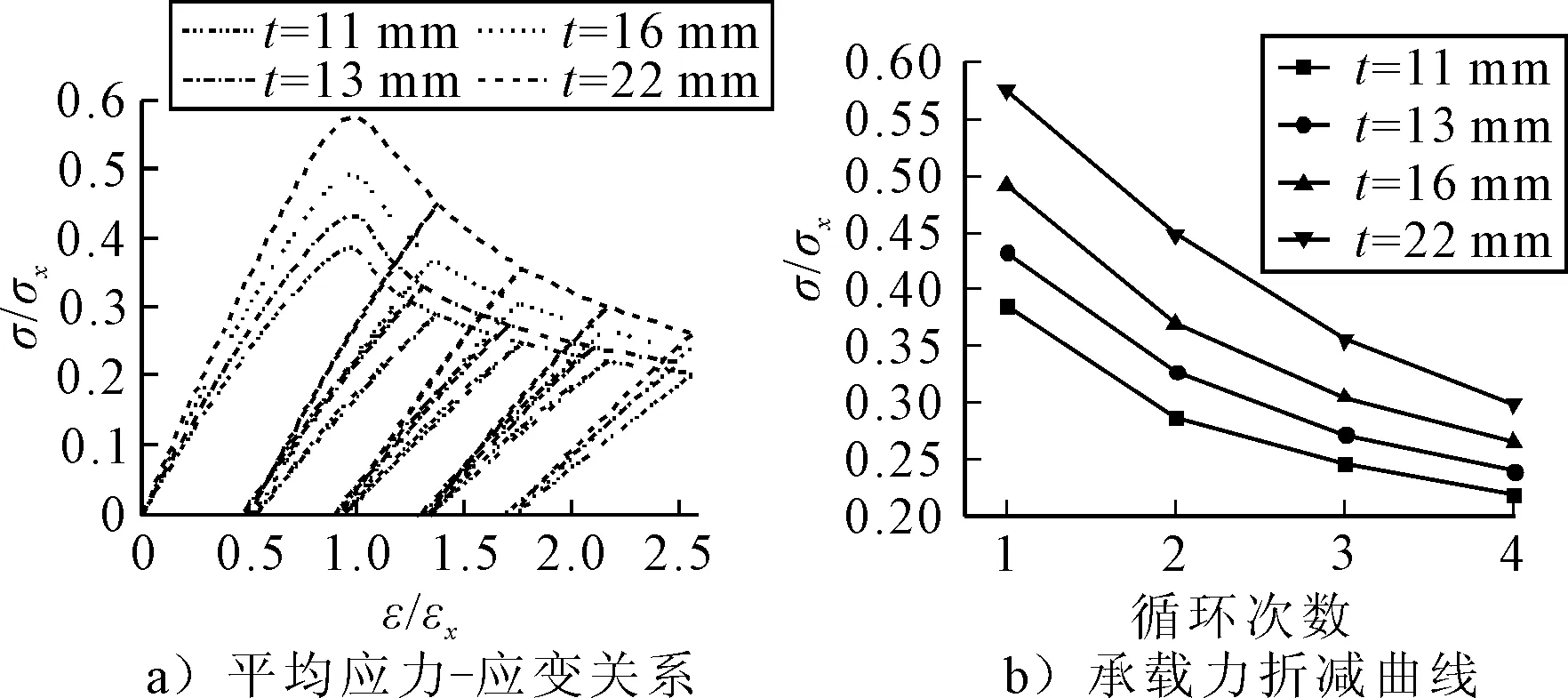
图3 模型4承载力随板厚变化曲线

2.3 裂纹长度对加筋板承载性能的影响

选取加筋板模型2和模型4来研究裂纹长度对加筋板承载能力的影响，其中加筋板的面板板厚均取为13 mm，加强筋的厚度则取为25 mm.为了方便进行对比，图4中也包含了完整板的无因次应力-应变曲线.

图4的无因次应力-应变曲线表明，在裂纹长度较小时，含裂纹加筋板的承载能力与完整加筋板并无太大差异，但随着循环次数的增加，两者之间的差距会逐渐加大.在第一个循环时，裂纹长度为0.1的加筋板的承载能力与完整板相差0.003 1σx，当进行到第四个循环时，两者之间则相差0.051σx.随着裂纹长度的不断增加，加筋板的承载能力会发生大幅地下降，与加筋板的承载能力和其有效承载面积相关这一结论相吻合.此外，随着循环载荷作用次数的增加，完整加筋板和裂纹加筋板的承载能力都发生了一定程度的下降，但裂纹加筋板的下降幅度明显高于完整加筋板，这与含裂纹加筋板在每次卸载后会产生较大的残余变形有关，但随着裂纹长度的增加，这种下降的趋势会减缓.

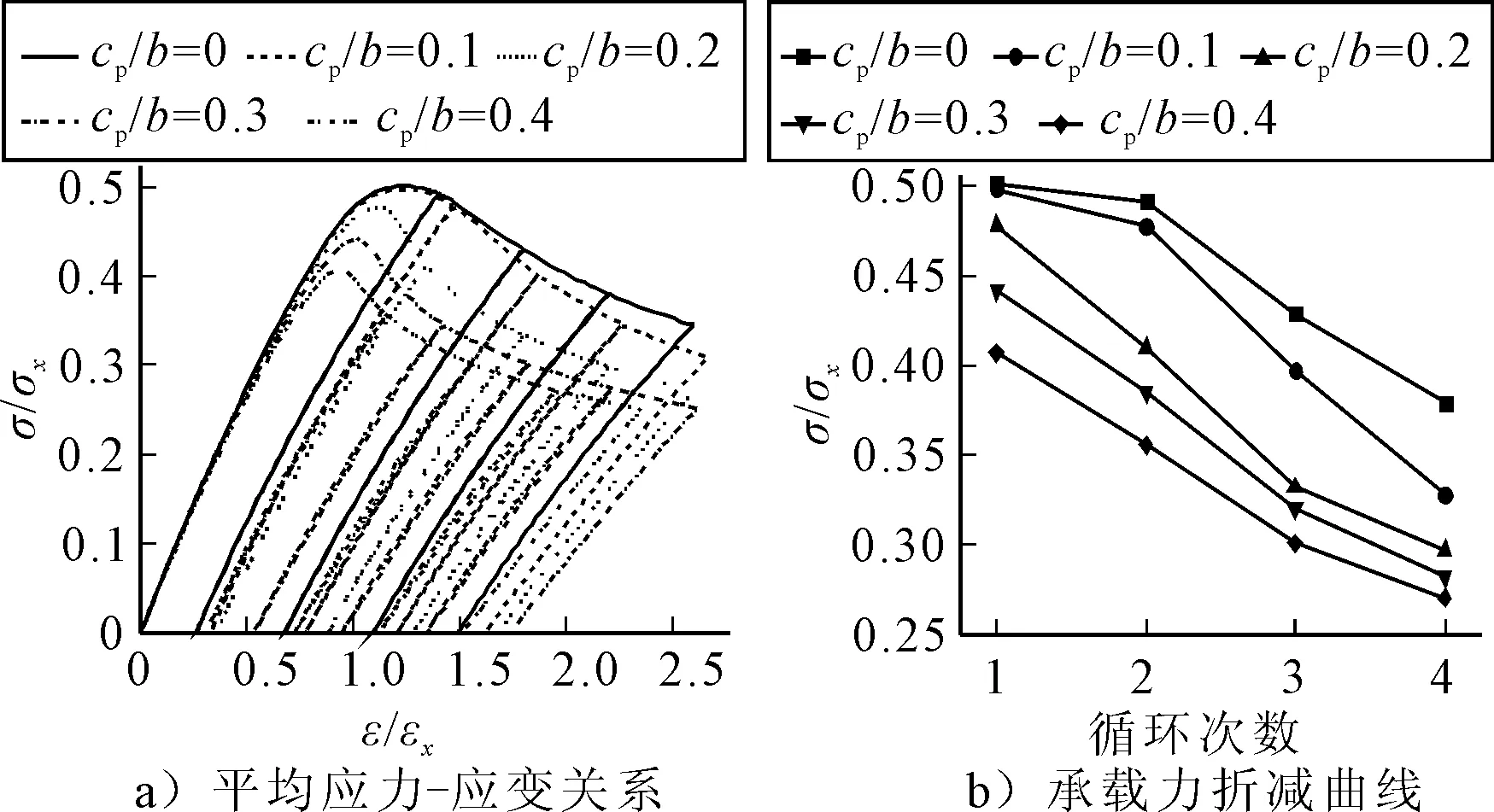
图4 模型二承载力随裂纹长度变化曲线

在相同的循环次数下，相比较模型二，加筋板模型四承载能力的下降幅度更大一些，这与加强筋上的裂纹削减了筋的一部分承载能力有关，见图5.此外，筋上的裂纹会恶化板筋交界处的应力分布，致该处塑性变形加大，对加筋板的承载能力也具有一定的减弱作用.总的来说，两种模型的下降趋势大体相同.

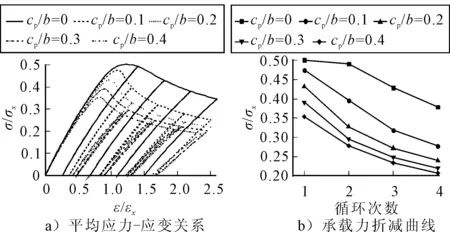
图5 模型四承载力随裂纹长度变化曲线

2.4 裂纹分布对加筋板承载性能的影响

选取图2的四种模型来探讨裂纹分布对加筋板承载能力的影响，加筋板上的裂纹长度cp/b取为0.2，加强筋上的裂纹长度cs/hw=0.2，加筋板的板厚均为13 mm.

图6的无因次应力-应变曲线表明，随着循环载荷次数的增加，四种模型的承载能力都发生了下降；模型一和模型二在所有循环中，承载能力的差距很小，表明在这种情况下裂纹的分布对加筋板承载能力的影响不大.在同样的循环次数下，模型三和模型四因为筋上存在裂纹，其承载能力明显低于模型一和模型二，并且其承载能力下降的幅度也明显高于模型一和模型二.在四种模型中，模型四表现出最为危险的情况，随着循环载荷作用次数的增加，在板筋裂纹交接处出现明显的应力集中现象并伴随着严重的变形，并且这种现象随着载荷作用的次数增加在不断加剧，这导致其承载能力下降的幅度高于另外三种模型.

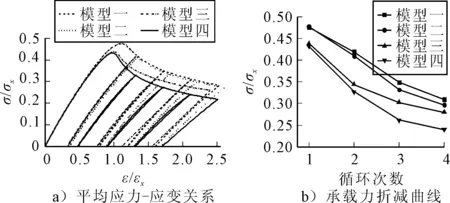
图6 四种裂纹分布对承载力的影响

2.5 侧向载荷对加筋板承载性能的影响

选取加筋板模型二和模型四来研究侧向载荷对加筋板承载能力的影响，其中加筋板上的裂纹长度cp/b取为0.2，加强筋上的裂纹长度cs/hw=0.2，加筋板的板厚均为13 mm，侧向载荷大小的选取文献[9]，载荷类型为均布面载荷，按大小分为四组，为了便于对照，不受侧压的含裂纹加筋板也包含在图中.

图7的承载力折减曲线表明，当侧向载荷的大小较小时，加筋板的承载能力与不受侧向载荷的加筋板差别不大，这表明较小的侧向载荷对加筋板的承载能力无太大影响；当侧向载荷不断增大时，加筋板的承载能力不断减弱，以模型四为例，当侧向载荷的大小为0.16 MPa时，加筋板的承载能力较不受侧向载荷的加筋板下降了16.4%，原因是当侧向载荷不断增大时，会使加筋板的初始面外变形加剧，这会极大的削减加筋板的承载能力.随着循环载荷作用次数的不断增加，两者承载力之间的差距在不断缩小，当进行到第四个循环时，两者之间的差距基本上可忽略不计，原因是随着载荷作用次数的增加，侧向载荷所引起的面外变形会在载荷往返作用时有一部分抵消，另一方面不受侧向载荷的加筋板的面外变形会随着循环次数的增加而不断加剧，这导致了两者之间的差距在不断缩小， 同时也与图7反映的两者承载能力下降速度相一致.所以侧向载荷对加筋板承载能力的影响主要体现在前些次循环，当载荷的循环次数达到一定的数目时，侧向载荷的影响可忽略不计.

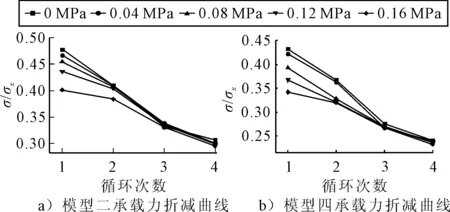
图7 侧压对加筋板承载能力的影响

3 结 论

1) 裂纹的存在会加剧加筋板的残余变形，使得在同样的循环次数下含裂纹加筋板的承载能力明显低于完整加筋板，并且裂纹的长度越长所造成的差距越大.

2) 侧向载荷对加筋板承载能力的影响取决于侧向载荷的大小，当侧向载荷较小时，两者的承载能力并无太大差距；当侧向载荷较大时，会导致加筋板出现较严重的初始面外变形，使加筋板的承载能力发生较大下降，但该变形会随着循环载荷作用次数的增加而抵消部分，因此当载荷的循环次数达到一定次数时，侧向载荷的影响可忽略不计.

3) 随着加筋板板厚的增加，其承载能力也会不断增加，这与厚板有更多结构参与抵抗变形有关；但随着循环载荷作用次数的增加，厚板的承载能力较薄板下降的更迅速，这应该是厚板的累计塑性变形更严重所导致的.

4) 在本文研究的四种模型中，板筋上都含有裂纹的加筋板表现为最危险的情形，应力最大区域出现在板筋裂纹交界处，导致该处出现较大塑性变形，对加筋板的承载能力起到削减作用，因此在实际的结构设计中应尽量避免出现裂纹交汇的情形.