气动冲击作用下钢桥疲劳裂纹闭合深度影响因素研究*
2020-06-03吉伯海袁周致远傅中秋
孙 童 吉伯海 袁周致远 傅中秋
(河海大学土木与交通学院 南京 210098)
0 引 言
钢材具有强度高、质量轻、塑性韧性好等优点,广泛应用于桥梁领域中[1].为了减轻质量,大跨径桥梁往往采用扁平钢箱梁作为主要截面形式[2].然而由于其特殊的结构体系及受力特性,在顶板与纵肋、横肋连接焊缝等重要构造细节处,疲劳问题较为突出[3],严重影响大跨度桥梁的服役性能.因此,当结构产生疲劳裂纹时,应当及时采取有效的维修措施,进行局部补强或消除裂纹裂尖应力集中,减少疲劳裂纹对结构造成的损伤[4].
常用的疲劳裂纹维修方法有止裂孔法[5]、钢板补强法[6]等.止裂孔法通过在裂纹尖端钻圆孔,消散裂纹尖端应力集中现象,是阻止疲劳裂纹扩展的临时性措施;钢板补强法则是在裂纹处固定高性能钢板,从而达到局部补强、延缓裂纹扩展的作用,但实际应用时往往由于连接件老化而达不到理想修复效果.近年来,钢桥裂纹气动冲击维修新技术得到了一定的发展[7],该技术以压缩空气为动力源,带动冲击头对母材表面进行高速冲击而产生塑性变形,使母材裂纹开口两侧自由面相互靠拢、挤压,形成裂纹闭合.裂纹开口闭合后局部区域应力重分布[8],裂纹面靠拢挤压引起的残余压应力可以减小甚至抵消焊接残余拉应力,改善裂纹周围的应力状态[9].国内外学者针对该技术已经展开了大量的研究.结果表明[10-11]:气动冲击作用下,裂纹尖端附近产生应力重分布,应力幅降低,能够有效延缓裂纹沿深度、长度方向的扩展,同时与传统的止裂孔修复措施相比,气动冲击维修技术具有更好的维修效果;有限元结果表明[12]:对裂纹闭合后的模型进行重新加载,拉伸荷载需克服闭合面压应力后才能重新张开,即裂纹重新张开前,冲击区域近表面均获得了一定的承载能力.总体而言,作为一种创新型的疲劳裂纹维修方法,该技术具有设备简单、操作方便、对母材构件损伤较少等优势,但对于裂纹的冲击维修方式尚无相关规定,同时评价该技术维修效果往往从改善应力状态、表面裂纹不可见等角度出发,而针对不同冲击影响因素下裂纹开口闭合深度以及不同闭合深度对裂纹扩展的影响等一系列研究相对较少.
针对以上问题,本文针对五种不同强度钢材带人工裂纹试件,开展不同冲击方法以及不同冲击参数下的冲击试验.分析了多种冲击因素组合下裂纹开口闭合形态以及闭合深度.同时,基于扁平椭圆裂纹模型建立扩展有限元模型,分析了不同裂纹闭合深度下应力强度因子的变化规律,并于基于Newman-Raju理论解进行对比,从裂纹闭合深度、延缓裂纹扩展等角度对气动冲击修复技术的维修效果进行简要评价.
1 试验概况
1.1 试件细节
试验所用试件为矩形钢条带裂纹试件,试件采用桥梁用钢,牌号分别为Q235qD,Q345qD,Q420qD,Q500qD,Q620qD,力学性能满足文献[13]的基本要求.由于只研究裂纹冲击后表面宏观形态的变化,在钢条宽度方向采取电火花线切割工艺制作人工裂纹,试件尺寸几何参数见图1a).矩形钢条尺寸为300 mm×25 mm×12 mm,沿钢条长度方向每隔30 mm设置人工裂纹,裂纹深度为6 mm,宽度有0.2,1.0 mm两种尺寸.裂纹从左到右以及编号,记为C1~C9.

图1 试件尺寸
1.2 冲击试验
首先选取强度为Q345qD、裂纹宽度为0.2 mm试件,开展不同冲击方式下裂纹开口闭合试验.将试件固定于台座,冲击头端部距离试件不大于5 mm,并与试件垂直,冲击参数采用5 mm×5 mm冲击头,90 Hz冲击频率.针对C1~C3裂纹,对裂纹开口部位进行单侧冲击;针对C4~C6裂纹,对裂纹开口部位进行双侧冲击;针对C7~C9裂纹,对裂纹开口部位进行三次冲击,见图2.
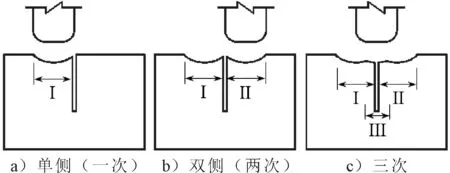
图2 不同的冲击方式
一次冲击-仅在裂纹开口部位一侧进行冲击;两次冲击-在裂纹开口部位的两侧分别进行冲击;三次冲击-在两次冲击的基础上,在裂纹开口部位正上方再进行一次冲击.
选取五种不同强度试件,开展不同冲击参数及影响因素下裂纹开口闭合试验.采取如上试验中三次冲击的方式进行试验,冲击参数包括:冲击头尺寸、冲击频率,冲击影响因素包括:试件强度、裂纹宽度,见表1.采取完全试验方案开展试验,共40种冲击工况组合,每种工况重复1次,最终进行80次冲击试验.
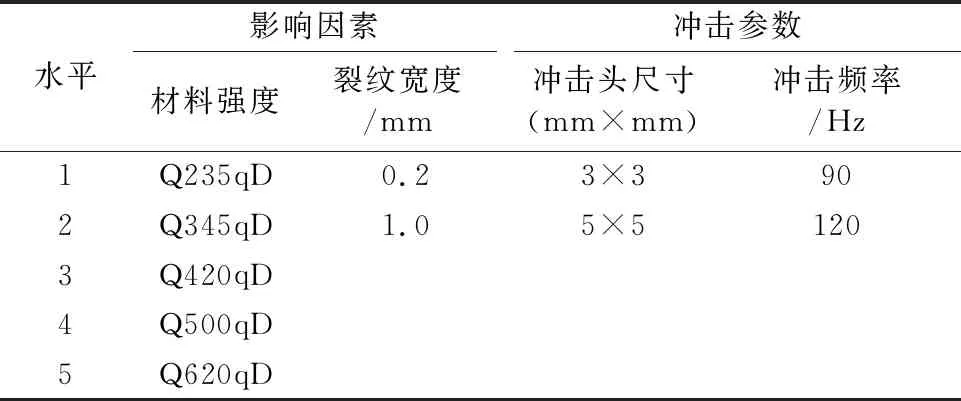
表1 试验参数表
1.3 裂纹闭合深度测量
在对裂纹开口部位进行冲击后,原先的裂纹开口消失,表面产生不规则的塑性变形.为了能够对裂纹闭合情况进行更加细致的测量及分析,将试件侧面打磨平整,采用“钢结构裂缝综合测试仪(ZBL-F800)”对裂纹开口部位的局部变形及闭合情况进行观察,并通过仪器的自主判断功能对裂纹的宽度、闭合深度等进行测量,见图3.

图3 裂纹闭合深度测量
2 试验结果分析
2.1 不同冲击方式下裂纹闭合深度
图4为不同冲击方式下裂纹开口局部闭合情况及其轮廓图.图4a)为一次冲击后裂纹开口局部变形.由于仅冲击裂纹右侧,右侧裂纹自由面在冲击应力波作用下产生横向与纵向的塑性变形,横向变形导致裂纹右侧自由面靠向左侧,形成一定深度的裂纹闭合,纵向变形导致试件右侧产生明显的凹陷.
图4b)为两次冲击后裂纹开口局部变形.在对裂纹左侧进行第二次冲击后,左侧自由面产生与右侧裂纹自由面相似的变形,两次冲击效应相互叠加,导致裂纹闭合深度明显增大.但同时裂纹两侧自由面的相对变形超过裂纹的实际宽度,在形成残余压应力的同时,约束作用下裂纹表面材料难以向四周变形,使得两侧接触面相互挤压,形成如图所示的凸起外形.凸起处形状不规则,容易引起新的应力集中,因此需要对凸起处作进一步处理.
图4c)为三次冲击后裂纹开口局部变形.第三次冲击后,裂纹表面凸起消失,裂纹表面相对平坦.同时由于凸起部位被压缩,使得局部塑性变形向下发展,但是由于裂纹闭合部位以及周围材料的环向约束作用,使得产生的塑性变形传递至未闭合的部位,进一步增加了裂纹的闭合深度.

图4 裂纹闭合面及轮廓图
图5为三种不同冲击方式下裂纹开口闭合深度柱形图.由图5可知,随着冲击次数的增加,平均裂纹闭合深度也不断增加;当对同一条裂纹进行三次冲击后,其平均裂纹闭合深度可达2.5 mm.
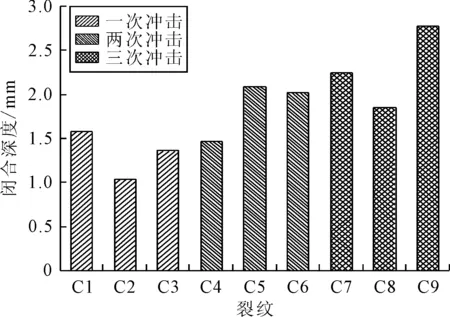
图5 不同冲击方式下裂纹闭合深度
2.2 不同影响因素下裂纹闭合深度
开展五种不同强度钢材不同参数冲击作用下的裂纹开口闭合深度试验,试验考虑0.2,1.0 mm两种不同宽度裂纹,分别代表疲劳裂纹萌生阶段和疲劳裂纹扩展阶段.前文可知,对同一条裂纹采用三次冲击的方式可以获得较平整裂纹表面以及较大的裂纹闭合深度,因此试验考虑两种冲击参数,采用三次冲击的方式进行冲击维修.
图6为不同冲击参数及影响因素下裂纹开口闭合深度.由图6可知,裂纹宽度为0.2 mm时,五种强度钢材的裂纹闭合深度均较深,最大深度可达2.0 mm,当裂纹宽度较大时(1.0 mm),冲击后裂纹开口闭合深度明显减小甚至无法闭合,表明气动冲击技术对小宽度裂纹具有更好的修复效果.同时对于高强钢材,近似的冲击波会产生相对较小的塑性变形,但同时塑性变形引起的塑性损伤更小,对于宽度较小的裂纹,采用合理的冲击参数也能使裂纹开口产生较大的闭合深度(1.5 mm),但总体而言,随着钢材强度的增大,裂纹闭合深度相对减小.

图6 五种强度钢材的裂纹闭合深度
总体而言,对于不同强度钢材,采用5 mm×5 mm的冲击头及90 Hz的气动工具可以使裂纹产生较大的闭合深度.相关研究表明,5 mm冲击头与3 mm冲击头可以产生较为相似的冲击深度,但5 mm冲击头冲击范围更大,冲击波在钢材内的传播深度更深,产生的横向变形更大,导致裂纹闭合深度较大.相较于120 Hz冲击频率,试验中90 Hz冲击频率下裂纹开口闭合深度更大,可能原因是:90 Hz冲击频率下,试验所用小型空压机达到气压稳定时可以达到较高的供气压力,即使冲击频率较低,但在单次冲击下可以获得更大的冲击力,综合而言,采用90 Hz冲击频率可以使裂纹自由面产生较大的塑性变形,获得更大的裂纹闭合深度.
3 不同裂纹闭合深度应力强度因子分析
3.1 有限元模型
气动冲击试验表明,采取适当的冲击方式以及冲击参数可以获得较大的裂纹闭合深度,但裂纹冲击闭合深度与延缓裂纹扩展之间的关系尚不明确.为此,建立带扁平椭圆裂纹的三维有限元模型[14],见图7,采用ABAQUS扩展有限元单元法,从应力强度因子的角度分析不同裂纹冲击闭合深度对延缓裂纹扩展的影响.模型尺寸为600 mm×300 mm×12 mm,材料本构为Q345qD本构模型,弹性模量E为206 GPa,泊松比υ为0.3,同时考虑了材料的弹塑性特征.采用扩展有限元XFEM模拟裂纹,在模型的中央位置,设置了一条长40 mm、深5 mm的扁平椭圆裂纹.模型的左侧部分固定区域,约束其各个方向的自由度,在其右侧表面设立100 MPa的拉应力,模拟典型的Ⅰ型张开型裂纹.在裂纹部位对网格进行了加密,最大网格尺寸为20 mm,最小网格尺寸为1 mm,网格单元采用C3D8R单元.
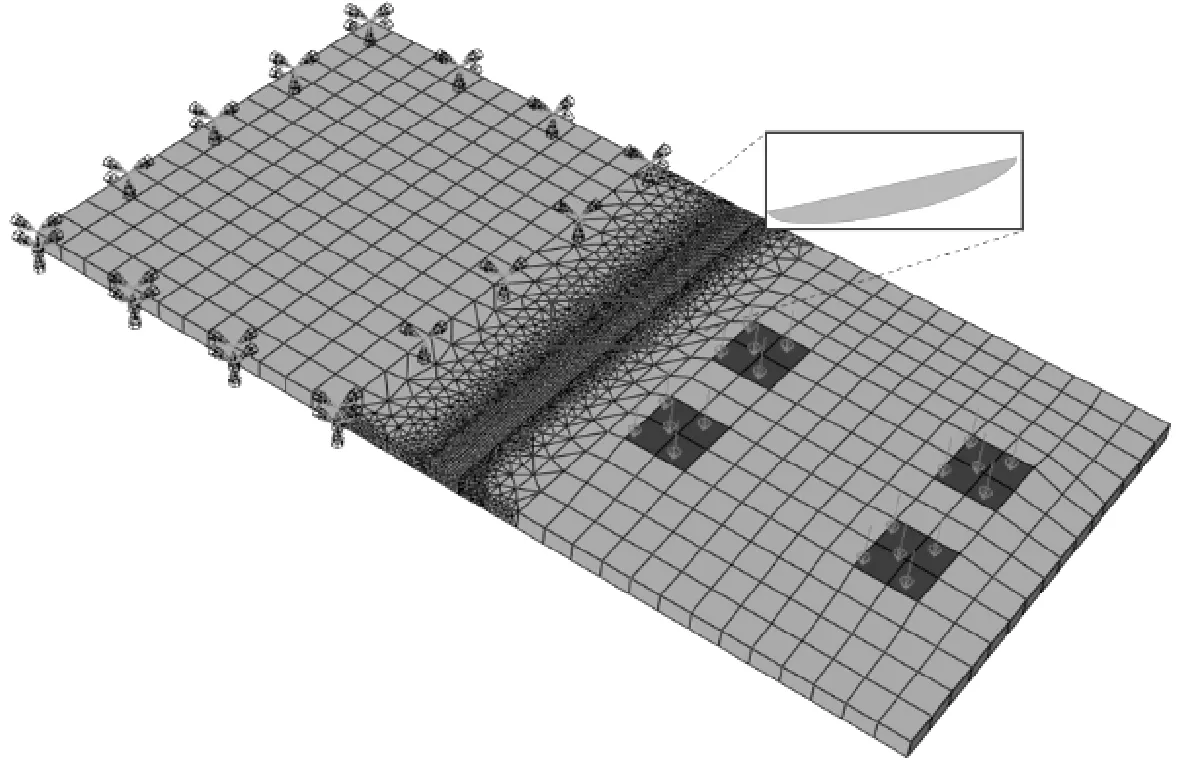
图7 有限元模型
在拉弯组合循环荷载作用下,扁平椭圆裂纹断面更符合实际桥梁中的疲劳裂纹.经过气动冲击维修后,裂纹表面的开口产生闭合,同时由试验可知,裂纹开口闭合深度可达2.0 mm.由此可以给出扁长型椭圆表面裂纹经过气动冲击维修后表面各点(B点)的应力强度因子K计算模型,见图8.裂纹闭合后,裂纹半椭圆模型的短半轴a的大小发生变化,为a-h,裂纹边缘有效范围为图中A~C区域.依据此裂纹闭合模型,建立裂纹闭合深度分别为0,0.5,1.0,1.5,2.0 mm五种工况下有限元模型,并比较不同裂纹闭合深度下裂纹尖端处应力强度因子变化情况.
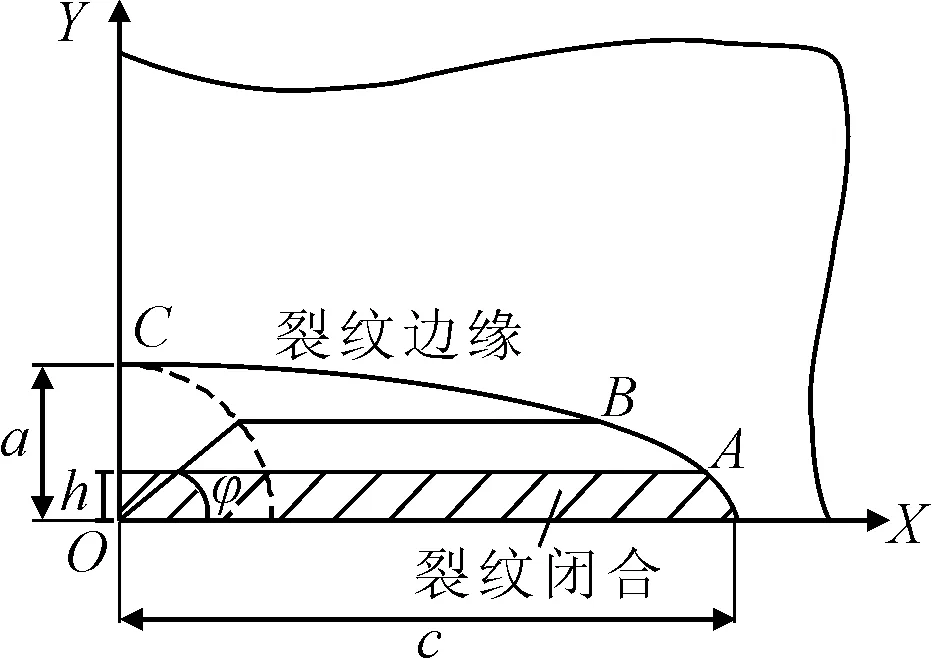
图8 冲击维修后裂纹模型
3.2 应力强度因子
采用Newman-Raju计算拉弯组合荷载下半椭圆形裂纹周边任一点的应力强度因子的公式为[15]
(1)
式中:σt和σb分别为名义拉伸应力及弯曲正应力;a为裂纹深度;c为裂纹长度的一半;t为板厚;w为板宽的一半;φ为Newman裂纹角;Fs等公式含义详见参考文献[16-17].
将裂纹未闭合时裂纹尖端应力强度因子理论解与有限元解相比较,见表2.扩展有限元方法求得的数值解在裂纹角为10°~30°时与理论解误差较大,误差值达到20%,其原因一方面网格仍较大,计算点未落在网格点上;另一方面当裂纹角为10°~30°时,所对应的裂纹边缘点相距较远,由于裂纹边缘具有奇异性,且有限元方法对处理高度非线性的扩展有限元仍存在一定误差,导致计算结果与理论解存在略微偏差.其余位置处误差较小,误差值仅为10%左右.同时随着裂纹角的大,理论解与有限元解在裂纹边缘处的应力强度因子变化趋势一致,当φ=90°时,即图8中的C点处,应力强度因子达到最大.因此,可以认为用该方法求得的数值解与理论解基本吻合,满足计算精度的要求.

表2 应力强度因子有限元解与理论解对比
提取在不同的裂纹闭合深度下,裂纹尖端C点与裂纹表面A点的应力强度因子,见图9.裂纹开口表面在冲击作用下产生闭合,其应力强度因子得到大幅度下降,在裂纹闭合深度仅为0.5 mm时,A点与C点的应力强度因子分别下降58.8%与37.5%,表明开口闭合后能够大大延缓裂纹扩展速率.随着冲击深度的增加,裂纹尖端的应力强度因子逐渐减小,但减小幅值趋于平稳,在裂纹闭合深度达到1.5 mm时,裂纹尖端A点与C点应力强度因子均达到较稳定值,从应力强度因子的角度表明气动冲击作用对延缓疲劳裂纹扩展速率起到了积极作用.同时,疲劳裂纹开口闭合后,裂纹前缘应力强度因子大幅度降低,但深度方向C点处KC仍然大于KA,表明冲击作用无法改变裂纹扩展状态,即沿深度方向扩展速率仍然大于沿长度方向扩展速率.
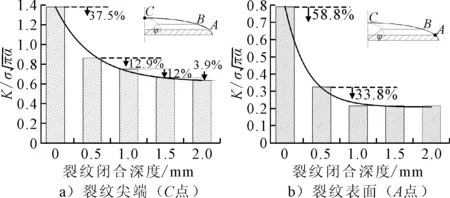
图9 不同裂纹闭合深度下应力强度因子
4 结 论
1) 冲击试验表明,对裂纹采取三次冲击的方式可以获得较大的裂纹开口闭合深度,同时冲击后表面更加平整,减少因表面坑洼引起的应力集中、冲击损伤等问题.
2) 当裂纹宽度较小时,采用合理的冲击参数可获得较大的裂纹闭合深度,本文试验中,最大裂纹闭合深度可达2.0 mm.当裂纹较宽时(1 mm),裂纹闭合深度较小,冲击作用不明显、
3) 有限元结果表明,裂纹开口闭合后,裂纹尖端应力强度因子大幅降低,且随着裂纹闭合深度增大,降低幅值趋于平缓.从应力强度因子的角度表明气动冲击作用对降低裂纹扩展速率起到了积极作用.
