基于TOBIT模型的越江隧道事故率影响因素分析*

陈 瑶 邢莹莹 陆 键 郎 洪

(同济大学交通运输工程学院 上海 201804)

0 引 言

越江隧道作为沿江(河)城市联结两岸的重要构造物已成为城市(如上海、武汉等)交通网络中必不可少的组成部分.由于隧道封闭性使得行车环境较为复杂，空气流通性差，一旦隧道内发生事故，其产生的烟雾和热量难以消散，极易引发火灾又阻碍了消防人员的救援行动[1].

国内外学者对隧道事故开展了大量研究，主要基于事故数据分析交通流、道路几何设计以及环境等因素对隧道安全的影响.Amundsen等[2]以挪威587条隧道的事故数据为基础，将隧道划分为4个区域，发现隧道事故率与隧道长度、交通量、车道宽度之间存在显著相关关系，并且发现不同区域的事故率及其严重程度也不尽相同.Lemke[3]通过分析德国68条隧道的事故时距，发现事故率与隧道长度之间存在正相关的关系，车道路肩的存在一定程度上会减少事故发生的可能性.Abedlaty等[4-6]研究通过建立相应的事故模型发现，隧道事故随着隧道长度、交通量的增大而增加.Kircher等[7]通过驾驶模拟试验发现隧道墙体的颜色的照明的亮度对驾驶员的行为产生了一定的影响，其中浅色墙体比强光照更能使驾驶员保持注意力的集中.

城市隧道其功能与城市快速路相似，其交通流状况影响着整个城市路网的通行效率.隧道结构的特殊性以及行车环境的突变，使得城市隧道易成为事故多发路段.胡文娟[8]通过分析城市隧道的交通特性与事故的特征，发现隧道出入口事故率较高，同时隧道事故与隧道长度存在一定相关性.通过分析隧道事故成因，得出车辆性能、隧道线形、天气情况、管理措施等也是影响隧道安全的重要因素[9].王雪松等[10]通过分析上海市翔殷路越江隧道的交通运行数据，认为车速运行的不一致性和隧道内车辆的变道是导致隧道追尾和侧碰事故的主要原因.驾驶人心理生理特征的变化与行车安全存在紧密联系，为掌握隧道驾驶员心理生理特征的变化规律，潘姝等[11]利用眼动仪，分析了驾驶员在城市隧道中的视觉分布特性，发现相对于隧道外部，驾驶人在隧道内部的视觉搜索效率降低，相同区域需要进行多次重复注视才能获取充分信息.冯忠祥等[12]利用生理测试仪采集了驾驶员在城市下穿隧道中的心率值，发现纵坡对驾驶员的心率存在显著影响，其敏感度高于速度的影响，其中下坡段心率增长率高于上坡段，驾驶员在下坡段更紧张.陈鹏等[13]通过分析隧道入口段驾驶员的瞳孔直径变化规律，计算得到隧道入口段不利于行车安全的区域.

国内外的研究主要关注隧道交通运行的特征以及隧道事故及其影响因素之间的关系，但研究对象多为公路隧道，对于越江隧道安全性的研究较为缺乏.John等[14]研究了越江隧道风险因素对隧道事故严重程度的影响，Jiang等[15]对越江隧道内的驾驶行为特性展开了分析，研究成果具有一定的实用价值和启示意义，仍缺少能从越江隧道的设计和管理的角度提供建设性指导的研究.城市越江隧道是城市交通网络的重要链接，且由于跨越河床的需求，其均为下穿式隧道，其入口和引导段的坡度较大，隧道出入口的标高差异较大.较大的坡度易增加控制行车速度与跟车间距的难度，出入口较大的高差缩减了驾驶员的视距.尤其在进入隧道的下穿段，驾驶员由于环境变暗、视线受阻，无法准确捕捉到前方的道路信息与交通状况，引起心理紧张程度提高，操作不当极易导致追尾事故.不同于普通城市下穿隧道，上海越江隧道横穿黄浦江，其长度均在2 km以上，其中崇明隧道长度达到了8.95 km.较长的隧道长度不利于隧道内事故及时撤离，从而容易引发二次事故，这也导致越江隧道的事故率高于普通隧道.

对于交通事故的研究分析多选用事故数作为评价指标或者预测变量，从量的角度描述影响因素与事故之间的关系.相对于事故数，事故率是一个相对指标，它既能反映事故的规模又能反映道路的安全水平，常作为评价交通安全水平的量化指标.因此，本文以越江隧道事故率为研究目标，结合越江隧道事故数据，着重从交通、道路线形以及环境等方面深度剖析其与隧道事故率之间的联系，分析事故发生的原因, 鉴别隧道事故的显著影响因素，从隧道设计和管理上改善隧道交通运营状况，提高隧道运营的安全性.

1 隧道路段划分

常用的路段划分方法有定长法和不定长法.定长法是指按一定长度将路线划分为均匀、等长的若干个路段，较少考虑事故点的分布状态.不定长法是指按事故点的集疏程度或道路特征对路段进行划分，路段长度不完全相同.

隧道不同于开放道路的显著特点是车辆进出隧道过程中光照的显著变化，在驾驶员的视觉上形成“白洞”和“黑洞”效应.同时，为了跨越河床，越江隧道通常比一般的城市道路或公路隧道具有更大的坡度和长度.因此,考虑到越江隧道的坡度特性以及隧道的进出口区域对驾驶员的视觉影响.本文采用不定长法将隧道分成五部分,其中路段区域1和区域5分别进入前和驶离后的区域，其长度为隧道洞口到地面交叉口的距离.区域2和区域4分别代表进入隧道和驶离隧道前的过渡区域，研究表明离隧道洞口的一段距离内，其隧道事故率显著发生变化，其距离的数值会随着不同的隧道而改变，为使过渡段充分包含这段距离，选取250 m作为过渡段的长度.剩下的部分即为隧道内部的区域3,见图1.

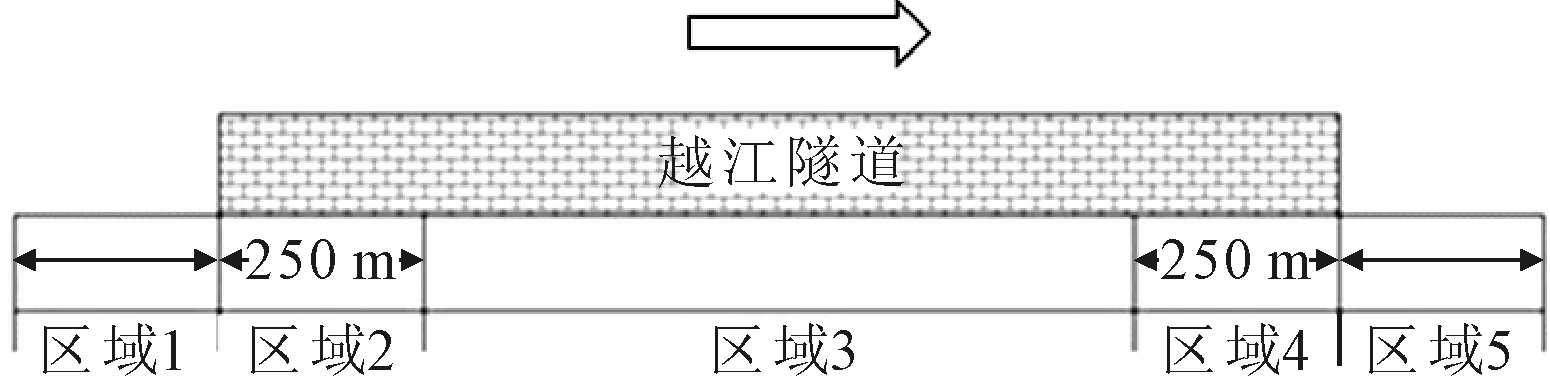
图1 隧道路段划分示意图

2 Tobit回归模型

事故数据是在有限的期间内进行统计的，某些路段可能没有事故记录，导致事故数据呈截尾数据.采用标准最小二乘对事故率进行建模可能会导致参数估计出现偏差.Tobit模型是解决截断数据建模分析的有效方法.考虑到事故率是连续非负的，因此取下界阈值为0，建立起隧道事故率与解释变量之间的关系，为

(1)

(2)

运用最大似然估计法对分布参数和模型参数进行估计, 似然函数为

(3)

式中：Φ为多元正态分布函数;φ为多元正态密度函数.

为了更好地理解变量对隧道事故的影响程度，引入弹性系数进行分析.在Tobit模型中弹性系数为

(4)

(5)

相应的似然函数为

(6)

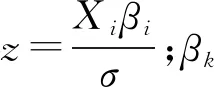
3 实证分析

本文从上海市公安事故数据库获取了上海市14条越江隧道2015—2016年的交通事故数据，共获取了4 467起隧道交通事故.每条事故数据包括事故时间和地点、事故类型、车辆类型、涉及车辆的数量、驾驶员信息、天气状况和伤害严重程度.另从和上海市交通委员会和上海市交通综合年报获取了14条越江隧道的年交通量、限速以及隧道的几何线形数据.14条隧道中有3条为双层越江隧道，外环隧道为三管隧道，其余隧道均为双管隧道，每条管道中均承载着单向越江交通.将每条管道划分为5个区域，以2015—2016年2年的数据为基础，共得到了350个路段单元.

隧道交通事故的发生是多种因素综合作用的结果，综合考虑道路线形、交通要素以及越江隧道的特性对事故的影响，选取了11个因素作为解释变量，见表1.其中，平均坡度指隧道不同区段坡度(绝对值)的加权平均值；最大坡度差表示下游段隧道坡度减去上游段坡度的最大绝对值.隧道长度变量为二元变量，根据文献[15]，1 000～3 000 m的隧道长度为记为“0”，超过3 000 m的隧道长度为记为“1”.同时为了反映同一段水平曲线与垂直曲线相互作用，引入“平纵组合比”变量表示纵向坡度与曲线半径之比.因变量为隧道不同路段的事故率，该指标定义为百万辆车事故率.

为了探究影响越江隧道安全的因素，首先采用Tobit模型进行回归预测，将全部自变量代入模型.其次，为了确定各变量对隧道事故率的影响程度，针对显著变量计算了各变量的弹性系数值，结果见表2～3.

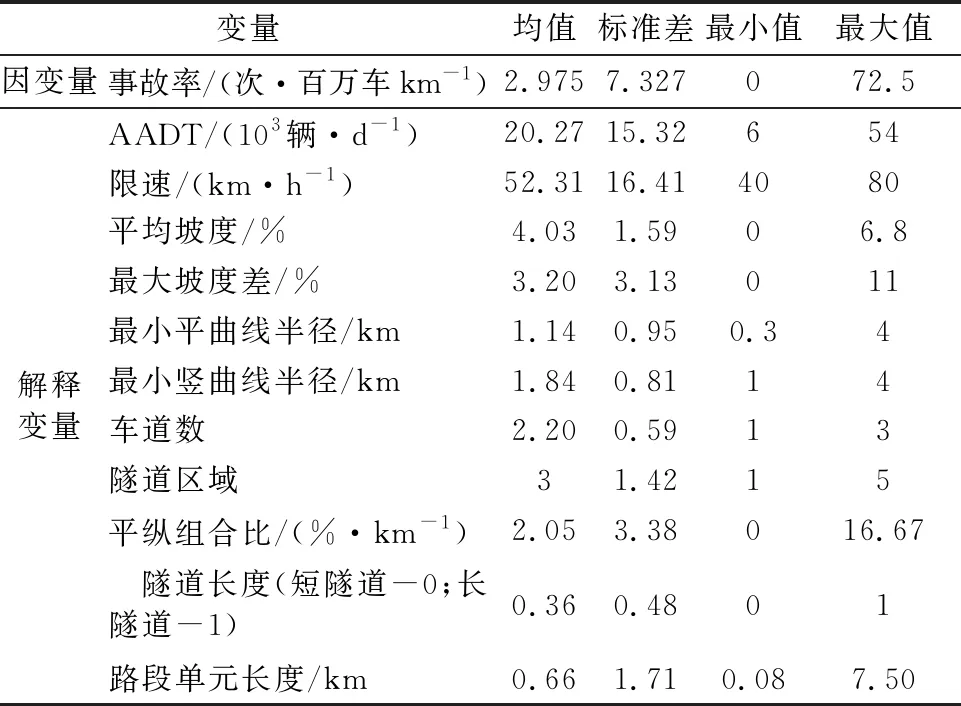
表1 越江隧道影响因素统计特性

表2 事故率tobit模型回归结果

注：**和*-95%和90%的置信度水平.

由表2可知，AADT、限速、坡度绝对值、最大坡度差、最小平曲线半径、最小竖曲线半径、平纵组合比、车道数以及隧道区域是影响隧道事故率的显著因素.

交通要素中，事故率随着交通量、限速的增大而增大.主要是因为随着交通量的增大，车辆间的间距逐渐缩小，车辆间的相互干扰也逐渐增多.若周围车辆出现不恰当的驾驶行为，极易影响驾驶员的驾驶状态，容易诱发交通事故.弹性系数表明，AADT每增加1%，则事故率上升0.135%.较高的限制速度使得驾驶员速度选择的区间变大，易造成较大的速度差，而较大速度差对安全存在负面影响.同时车辆以较高速度行驶时，同等条件下驾驶员的反应时间变短，操作不当则极易导致追尾事故.

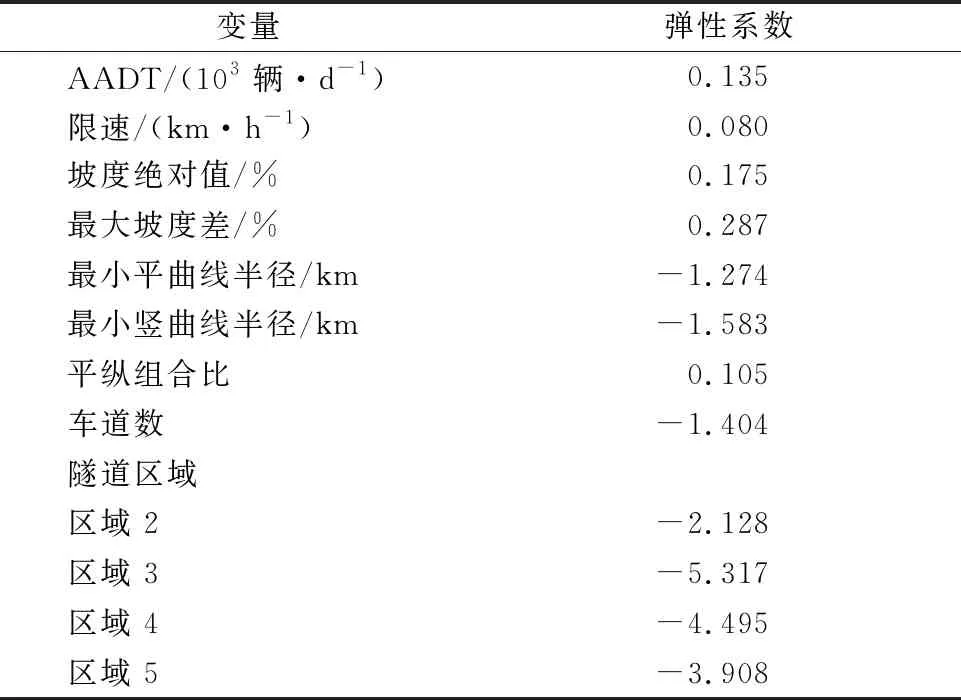
表3 弹性系数分析

在道路线形要素点中，坡度是影响隧道事故率的显著变量，并且事故率随着坡度绝对值的增大而增大.较大的坡度增加了驾驶的难度，尤其是在下坡路段，驾驶员可能需要采取频繁制动来保持稳定行驶，频繁制动易造成车辆制动性能下降，同时也易诱发追尾事故.坡度的弹性系数也表明，坡度绝对值每增加1%，则事故率相应地增大0.175%.同时坡度差也对事故率存在着负面影响，坡度差每增加1%，事故率随之增大0.287%.

事故率与隧道最小平曲线与最小竖曲线之间均呈负相关.较小的平曲线半径下，道路线形的变化将变得急促，而隧道边墙的遮挡使得这种急剧的变化难以被驾驶员识别，并且小半径曲线也会来带离心力的急剧变化，致使驾驶员无法及时做出相应的反应，容易导致事故的发生.同样，小半径的竖曲线半径也使得车速更加难以控制.并且城市越江隧道多为凹形竖曲线，相比于凸型竖曲线，在凹曲线上车辆行驶时产生的增重感会使驾驶员感到不适.已有研究也表明，同一半径下，凹形竖曲线事故率也高于凸型竖曲线.平曲线和竖曲线的弹性系数表明，半径每增大1%，事故率分别降低1.274%和1.583%.小半径的平曲线和竖曲线都会导致视距不足的问题，不利于保证行车的安全性.为了衡量平纵断面共同作用的影响，本文引入平纵组合比参数对其进行分析.回归结果表明，隧道事故率随着平纵组合比的增大而增大.

车道数与隧道事故率之间呈负相关，随着车道数的增加，路面宽度也随之增加，一定程度上可以减轻隧道边墙对于驾驶员的负面影响，从而提高了行车的安全性.其弹性系数表明，车道数每增加1%，其事故率降低1.414%.

由模型结果可以看出，隧道区域位置是影响隧道事故率显著变量.从回归系数可以看出，隧道进口前的路段(区域 1)事故率最高，其次为靠近隧道进口的过渡段(区域2).隧道进口处是地面道路与隧道的连接处，其在限速、坡度、车道、行车视距等方面的变化，增加了驾驶难度.此外，部分隧道进口紧邻城市交叉口与城市高架快速路出口，其车流量较大，交通运行的状况也较为复杂，地面、地下交通流交织运行产生大量交通冲突，极易诱发事故的产生，因而导致区域1的事故率最高.相比白洞效应，黑洞效应造成的行车危险性更高，因而区域1和区域2的事故率高于区域4和区域5.弹性系数表明，相比于区域1，区域2至区域5的事故率分别下降2.128%、5.317%、4.495%、3.908%.

对于隧道中间段(区域3)，由于越江隧道中间段坡度、线形变化均为平缓，见图2，并且驾驶员已经经过了明暗适应性的阶段，配合隧道内的行车指引与提示设施，驾驶员在隧道内的行驶更加谨慎，因而隧道中间段事故率最低.

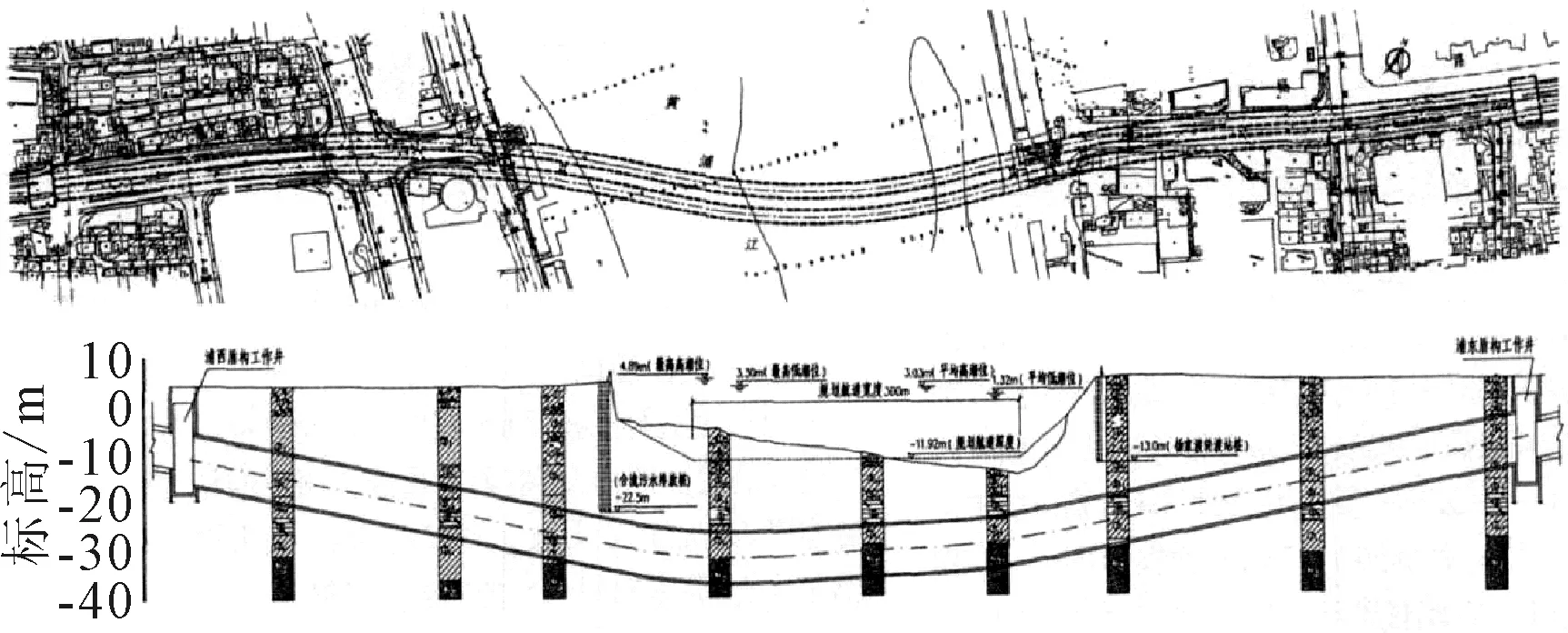
图2 复兴东路隧道平面及纵断面图

4 结 论

1) 隧道事故率随着交通量的增大而增大.交通量的增大使得车辆间的间距减小，车辆间相互干扰易诱发交通事故.

2) 隧道限制速度的增大，事故率也随之升高.较高的限制速度易导致较高的行驶速度，同时更易增大车辆之间的速度差异，对行车安全不利.

3) 隧道平均坡度越大，对车速的控制难度也越大，因而事故率也随之增大.隧道事故率也随着最大坡度差的增大而增大.

4) 平曲线半径越小，驾驶员越难识别线形的变化；竖曲线半径越小，视距越小，驾驶员对速度越难控制；避免纵坡较大的路段设置小半径的平曲线.

5) 隧道进口处(区域1)事故率最高，其次为进口处过渡段(区域2).隧道出口处(区域5)及其过渡段(区域4)事故率较低，中间段(区域3)事故率最低.