一类高分数阶微分方程边值问题解的存在性
2020-06-03禾丁予
禾丁予
(天津大学数学学院, 天津 300350)
(2010 MSC 34A08,34B15)
1 引 言
分数阶微分方程在粘弹性力学、非牛顿流体力学、高分子材料和自动控制理论等领域有着广泛的应用[1-2].近年来,国内外学者对分数阶微分方程边值问题解的存在性研究也取得了重大进展[3-10].如,文献[8]研究了以下分数阶微分方程边值问题
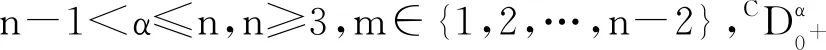
2 预备知识
定义2.1[1]函数y:(0,)→R的阶数为α>0的Riemann-Liouville分数阶积分定义为
定义2.2函数y:(0,)→R的阶数为α>0的Caputo分数阶导数定义为
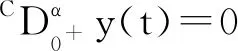
y(t)=C0+C1t+…+Cn-1tn-1,
其中 Ci∈R,i=0,1,…,n-1,n如定义2.2所述.
引理2.4设y∈Cn(0,1)∩L(0,1)有α>0阶分数阶导数.则
Cn-1tn-1,
其中 Ci∈R,i=0,1, …, n-1,n如定义2.2所述.
记
(2)
其中h=0,1,…,n-1. 选取适当的λ,使得
(3)
引理2.5设y∈C[0,1],n-1<α≤n,n≥3,λ∈R+,m∈{1,2,…,n-2}.若(3)式成立,则边值问题
有唯一解
(7)
证明 设u为方程(4)的解.由引理2.4知
Cn-1tn-1,Ci∈R,0≤i≤n-1
(8)
(8)式可以变形为
Cn-1tn-1]eλt.
上式两边在0到t上积分可得
(9)
由(5)式可得
Ci=0,i=0,1,2,…,m-2,m+1,…,n-2,
且λCm-1-mCm=0.将上式代入(9)式可得
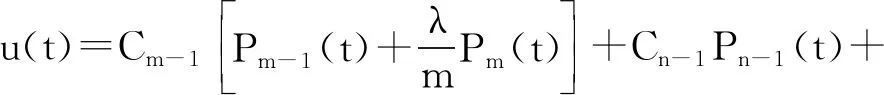
由Ph(t)的表达式(2)计算得
所以
(10)
由边值条件(6)可得
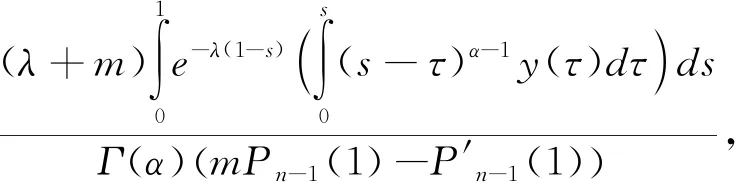
因此
证毕.
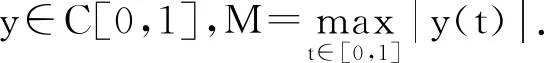
证明 仅证(ii).
证毕.

引理2.8(Banach压缩映像原理[10]) 设(X,‖·‖)是一个Banach空间,Ω⊂X是一个非空闭集,且T:Ω→Ω.若存在α∈[0,1)使得对任意的x,y∈Ω,有‖Tx-Ty‖≤α‖x-y‖,则有唯一的x*∈Ω,使得Tx*=x*,即 x*是算子T的唯一不动点.
3 主要结果
令E=C1[0,1].取范数
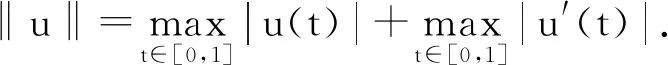
则(E,‖·‖)为Banach空间.定义
令
引理3.1算子T:E→E为全连续算子.
证明 由函数f的连续性可知,算子T连续.设Ω⊂E为有界集,则存在常数N>0,使得对任意的u∈Ω,有‖u‖≤N.记
L=max{|f(t,u,v)|,(t,u,v)∈[0,1]×[0,
N]×[0,N]}.
由引理2.6,对任意的u∈Ω,有
所以T(Ω)一致有界.
另一方面,设0≤t1 所以T(Ω)等度连续.由Arzela-Ascoli定理知,算子T全连续.证毕. 记 2+M2}. 定理3.2设f:(0,1)×R×R→R是连续函数,且存在非负连续函数ρ0,ρ1,ρ2使得 |f(t,u,v)|≤ρ0(t)+ρ1(t)|u|+ρ2(t)|v|, t∈[0,1],u,v∈R, 且满足 则边值问题(1) 至少存在一个解. 证明 由引理3.1知算子T:E→E为全连续算子.下证集合V={u∈E:u=μTu,0≤μ≤1}有界.对任意的u∈V,t∈[0,1],有 u(t)=μTu(t),u′(t)=μ(Tu)′(t). 放缩得 |u(t)|+ρ2(t)|u′(t)|), |u(t)|+ρ2(t)|u′(t)|). 因此, ‖u‖≤ 所以集合V是有界的.由引理2.7,算子T至少有一个不动点,即边值问题(1)至少存在一个解.证毕. 定理3.3设f:(0,1)×R×R→R是连续函数,且存在非负连续函数γ1,γ2,使得 |f(t,u1,v1)-f(t,u2,v2)|≤ γ1(t)|u1-u2|+γ2(t)|v1-v2|, t∈[0,1],ui,vi∈R,i=1,2. 且满足 则边值问题(1)有唯一解. Br={u∈E:‖u‖≤r}, 其中 先证T(Br)⊂Br.对任意的u∈Br,有 同理 因此‖Tu‖≤r. 另一方面,对任意的u,v∈Br,t∈[0,1],有 同理 则 例4.1考虑边值问题 f(t,u,u′)=k1(t)sinu+k2(t)sinu′+g(t). 计算可得 M1=1,M2=1.6150, A1=1.3823,A2=2.2384. 又因为 |f(t,u,u′)|≤|k1(t)||u|+ |k2(t)||u′|+|g(t)|, 由定理3.2,只要 该边值问题就至少存在一个解. 例4.2考虑边值问题 计算可得 M1=1,M2=1.3540. A1=0.3893,A2=0.5442. 另外,我们有 |f(t,u,u′)-f(t,v,v′)|≤ 取 则有 0.6601<1. 由定理3.3,该边值问题有唯一解.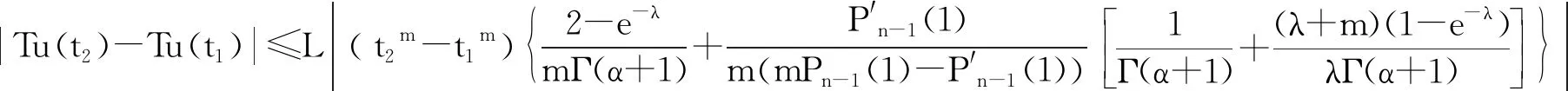
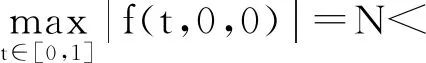
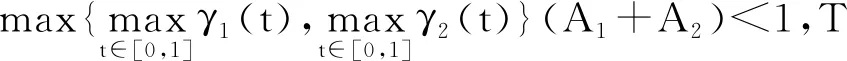
4 例 子