基于速度选择切换型视线法的无人帆船循迹航行

袁鹏，徐泓燊，张雪飞，谭俊哲,2，王树杰,2，惠文海,2

1 中国海洋大学 工程学院，山东 青岛 266100

2 青岛市海洋可再生能源重点实验室，山东 青岛 266100

0 引 言

无人帆船在水域航行时，主要受风以及由风引起的浪和流等许多因素的影响，这些复杂的环境因素决定了帆船航行比其他机动艇航行的难度更大。因此，无人帆船的循迹航行需要考虑多种环境因素，根据观测点的气象信息来实现其循迹航行。

目前，多所高校和科研院所开展了一系列无人帆船路径规划和循迹航行方面的研究。王倩等[1]根据操舵的专家经验制定出了245 条模糊控制规则，直接以舵角作为单输出，实现了一个1.5 m 帆艇的循迹航行。邢慧丽等[2]针对帆船在海上行驶所具有的模糊性和不定性特点，提出了基于分区段优化和进化规划的帆船航行路径优化方法，对每一个分段都制定相关决策评价函数，利用全局优化搜索路径，得到最优方案。葛艳[3]提出了基于进化规划理论的无人帆船行驶最优路径规划方法。康梦萁等[4]针对无人帆船短途路径规划问题提出了速度最优法，并将其与传统的A*算法进行了对比，结果证明了速度最优法在短途路径规划中的合理性。董早鹏等[5]针对水面无人艇（Unmanned Surface Vehicle, USV）的非对称和欠驱动特性，提出了一种非对称模型下的改进视线法导向路径方法，有效解决了针对欠驱动无人艇的航路点路径跟踪问题。曾江峰等[6]设计了一个新的切换型视线法制导律，可以引导USV 始终以最佳视线圆半径趋向期望路径。

帆船的动力来源主要依靠风力，且只要有风就会伴随有浪、流对船体的影响，这些影响在实际航行中是不容忽视的因素；依靠流体动力学、通过设置流场环境得到的帆船航速往往需要插值才可以使用。在此基础上，再结合诸如遗传算法、蚁群算法、模拟退火算法之类的算法进行路径规划，这使得整个求解过程时间较长。而视线(Line of Sight，LOS)法因简单、快速、高效，已在路径规划跟踪系统设计中得到了普遍应用[7-9]。在传统的LOS 路径规划中，路径跟踪点的LOS 视线圆半径通常设定为固定不变[10]，虽然其整体形式简单，但会导致收敛时间过长。后来，学者们又提出了比例型LOS[11]和指数型LOS[12]。与比例型LOS 相比，指数型LOS 在路径跟踪误差收敛性方面得到了显著改善，但因为其数学模型中引入了指数函数、朗伯W 函数，使得求解LOS 角的运算时间较长。

针对上述问题，本文拟提出一种速度选择切换型LOS 法，通过无人帆船速度预测程序（Velocity Prediction Program，VPP）模块，使无人帆船在每个航速方向能够达到的较大速度的基础上，再结合切换型LOS，使得路径跟踪误差收敛性得到改善，并使LOS 角求解运算量明显减小。

1 无人帆船循迹航行流程

无人帆船的循迹航行必须具有应对水面波、流多变情况的适应性以及实时控制的灵活性，整个控制流程如图1 所示。根据在气象站点测量得到的风况信息判断是否满足帆船航行的基本条件，并通过帆船各个传感元器件为智能航行进行初步调节，在得到相应的风速、风向与实时坐标之后进行速度预测，同时通过循迹模块获得最佳期望航向角与帆角，然后，再通过下层搭建的控制模块实现无人帆船的循迹航行，并通过传感器模块对帆船的姿态、航向、位置等信息进行实时监控。因此，在无人帆船的自动循迹航行中，求解出航行速度是算法实现的关键所在。

图 1 无人帆船循迹航行流程图Fig. 1 Flow chart of unmanned sailing boats path tracking control

2 算 法

LOS 法的原理是在预期航迹上设定一参考点，并有一定的距离在帆船的前方，通过实时不断地调整航向，使被控帆船保持对准LOS 角，并达到期望路径的位置，从而实现航迹跟踪的效果[7-8]。帆船在行进过程中受风力影响造成的横向偏移较大，一般的横向轨迹误差法无法保证稳定性[13]，而LOS 法能使航向偏差不断减小直至为零，因此在航向角偏差较大时适宜采用LOS 法。同时，结合不同帆船所具有的不同速度极曲线图对应的速度数据即可完成无人帆船的循迹航行。

2.1 无人帆船速度预测

由于帆船属于无动力航行，因此需要尽可能考虑风对帆船升力或阻力的影响。在陆地上感知的是绝对风速和风向，在船上感知到的风速是相对风速和相对风向，引入船速后，三者满足如图2所示的速度矢量三角形关系。图中：VB为静水船速；VW为相对风速；θW为相对风向角；θT为绝对风向角；VT为绝对风速。

图 2 速度矢量三角形Fig. 2 Triangle of velocity vector

根据余弦定理可得如下公式[1]：

帆船是依靠自然风力作用于帆上产生伯努利效应而推动船只行进的。帆船在海上的运动可以近似看作六自由度刚体运动。为了方便研究，只考虑水平运动而忽略横摇、纵摇、垂荡运动，将其简化为三自由度运动模型。帆船平面运动的各角度关系如图3 所示。图中：α为迎风角，即帆与相对风之间的夹角；β为帆的调整角，又称转帆角，即帆与航向之间的夹角；θW=α+β-θ，其中θ为船的漂角；δ为舵角；V为船速。以大地坐标正北方向为基准，顺时针方向风向角为正值，逆时针方向风向角为负值。

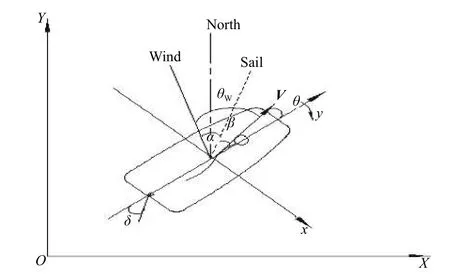
图 3 帆船行驶平面角度示意图Fig. 3 Schematic diagram of sailing plane angle

通过对行驶中帆船的受力分析，在平静的海面上如果不考虑海流和波浪对船体的各种干扰力以及力矩时，船速和风速之间的关系近似为[1,6]

式中：ρ为水的密度；S为帆的面积；C为阻力系数[14]。

因此，在帆船实际求解速度的过程中，需要结合帆船的帆、舵以及船舶主尺度参数和水面实时气象数据进行综合运算，通过VPP 模块实现对无人帆船航速的求解。VPP 建立在风帆空气动力模型和船体水动力模型的基础之上，通过风帆空气动力与船体水动力建立力平衡方程与力矩方程[15]，进而求得帆船在各种航行状态下的速度。VPP 的速度求解需要迭代计算。首先，由绝对风速、风向以及初始船速，结合速度三角形求出相对风速、风向，从而求出风帆空气动力；然后，利用初始横倾角，结合横倾方程求解相应的横倾角，对计算出的横倾角进行校核，重复计算直到横倾角迭代收敛，依据计算出的横倾角和初始船速，利用水动力与空气动力平衡方程联立求解力系平衡，计算出相应的船速和偏航角等。帆船最佳航线是以VPP 速度计算为基础，以航行时间最短为目标函数，求得各条航线上的航行时间。

无人帆船首先根据目标点确定航速方向范围，根据风速、风向在排除逆风不可航行区域，即−36°～36°范围后（不同船只范围有所不同），对剩余的方向角度通过VPP 模块进行速度计算得到航速，并将每一个航速投影到起始点连线上，从中选择较大航速值，则选择的航速方向就是帆船下一目标点的航向。同时利用切换型LOS 对无人帆船的航迹进行实时调节修正，直到到达期望航向点。

2.2 无人帆船速度选择切换型视线法

只要使无人帆船的航向保持对准LOS 角，并结合速度选择法进行角度选择，在行进过程中不断修正调整，帆船就能达到期望的目标点，所以获得LOS 角是算法的关键所在。

图4 所示为LOS 算法原理图。图中：P（x,y）为帆船的当前位置；Pk(xk，yk)为帆船在航段内的期望位置，Pk-1(xk-1，yk-1)为上一次的期望位置，两点之间的距离可以进行测量[11]；PLOS(xLOS，yLOS)为帆船的期望可视距离点；Δ为前视距离，即帆船当前位置与期望点PLOS(xLOS，yLOS)在预期航迹上投影点间的距离，根据经验可知，Δ=nLD，其中LD为帆船的总长，n为整数，通常取为3～5；d为帆船的横向跟随误差；α1为正北方向与预期航线的夹角；ψ为帆船的航向角；ψ1为航向偏差角；α2=ψLOS，为LOS 角。由图中可知，ψ1=α2-ψ，在航行过程中，当ψ1趋于无限小的时候帆船就向目标点行进，并将最终达到预期航线。

LOS 角ψLOS可以通过式（4）计算得到。

图 4 LOS 算法原理图Fig. 4 Schematic diagram of LOS algorithm

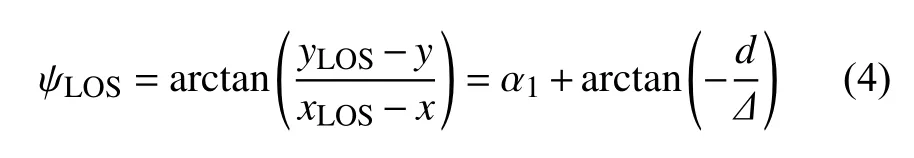
式中，ψLOS的范围为（−π，π）。

图5 所示为切换型LOS 算法的示意图。当帆船进入该预期航向点Pk(xk，yk)一定范围内时，便自动放弃向该航向点的行进，转入跟踪下一个预期航向点Pk+1(xk+1，yk+1)，而当帆船偏离期望航迹一定距离d之后，前视距离Δ会进行切换，更新原目标点，保证帆船偏离预定航迹较小。这样就需要一个标准来对期望航向点进行判别和切换，本文采用的是一种基于最短距离、同时具有快速收敛特性的切换型LOS 法。图5 中：Pt(xt，yt)为帆船在t时刻的位置；R1为切换型LOS 的切换圆半径；R2为比例型LOS 的切换圆半径；Rmin为LOS 最小切换圆半径；Rk为下一个预期坐标点的圆半径。LOS 位置通过式（5）确定。

式中，R为LOS 圆与预期航线相交或相切的圆的半径，也就是切换型和比例型这2 种圆的半径。为了保证式（5）有解，需要保证R≥d[16]。因此，在条件允许的情况下R必须设置得充分大。但是，这会映射出较大的前视距离Δ，导致帆船到达期望路径的收敛时间较长。为此，提出了切换形式的R1以及比例形式的R2来缩短收敛时间。切换形式满足式（6）：

比例形式满足式（7）：

与比例型LOS 相比，切换型LOS 是一种全新并基于最短距离趋近方法且运算量较小的策略。在式中规定：当|d|≤Rmin时R=Rmin，这能使帆船以较大的速率消减由于风力所造成的路径跟踪误差；当|d|＞Rmin时R=|d|，该策略可以使帆船在行进过程中按最短距离的方向趋近于预期路径。在图5 中，基于所提出的切换型LOS，LOS 圆半径的变 化 为R1→Rmin，其 中R1为|d|＞Rmin时 的LOS 圆半径。比例型LOS 圆半径的变化情况为R2。

无人帆船路径规划速度最优法是一种动态规划方法，其核心思想是保证无人帆船具有以较快速度达到终点的能力，因此可能会存在为获得最优速度而偏离期望航线过大、造成路径长度较大的问题，而利用切换型LOS 不断趋近期望路径的优点，可有效减少无人帆船为获得最大速度导致横向跟随误差较大的问题，将两者结合，既保证了无人帆船速度较优，也防止了循迹航行的不合理。

3 仿真分析

图 5 切换型LOS 算法示意图Fig. 5 Schematic diagram of switching LOS algorithm

无人帆船模型的主要参数及物理模型分别如表1 和图6 所示。通过VPP 模块得到了帆船的速度极曲线，如图7 所示。图7 表示在不同绝对风速下，帆船与风向所成的不同角度所具有的较优船速。一般认为帆船在相对风向角处于−40°～40°，即处于顶风航行阶段时，为了具有合理船速，就不能按照预定的最短路线行驶。例如，在正顶风航段，即相对风向角为0°～36°时，帆船处在不可航行区域，所以在速度极线图中0°～36°之间没有速度显示，帆船处于失速状态。为了使帆船获取动力，就需要按照之字形路线行驶，不断地迎风换舷，而在逆风状态下，不同间隔对路径轨迹与耗时有一定影响，本次规定逆风仿真路径的计算间隔为40 m进行一次迎风换舷的调整，以保证帆船以合适的速度行驶。

表 1 无人帆船尺寸参数Table 1 Size parameters of unmanned sailboats

图 6 无人帆船物理模型Fig. 6 Physical model of unmanned sailing boat

图 7 无人帆船速度极线图Fig. 7 Polar diagram of unmanned sailing boat's velocity

在风向恒定、风速为6 级（10.8～13.8 m/s）情况下测试无人帆船完成一个边长为100 m 的正方形闭环区域的循迹航行。设置风向为正北方向，以此可以完成横风、顺风与逆风等不同情况下的航行，仿真结果如图8 所示。由图中可以看出，速度选择LOS 法相比单一的速度选择法具有更好的规划路线。图9 所示的位置误差和图10 所示的航向角偏差结果也表明，速度选择LOS 法具有相对较小的误差数据。表2 所示为2 种方法在每一段规划路径所花费的航行时间。由表中可以看出，速度选择LOS 法循迹航行的时间更短，均方根误差（RMSE）较小。

图 8 路径规划仿真对比图Fig. 8 Comparison of path planning simulation

图 9 位置误差对比图Fig. 9 Comparison of position errors

图 10 航向角偏差对比图Fig. 10 Comparison of heading angle deviation

表 2 两种算法不同航段耗时Table 2 Time-consuming of two algorithms in different sections of voyage

4 试验对比

试验使用的控制板有主控板和驱动板，配备的传感器包括超声波风速风向仪、帆角编码器、电子罗盘和GPS，信号传输采用GPRS 与2.4 GHz无线通信。在地面基站处采用无人帆船监控软件监视实时返回的数据和控制数据。无人帆船监控软件是使用Visual Studio 编写的MFC 应用程序，可实时监控船舶状态、修改参数、记录数据文件等。该执行信号由基站通过Modbus 传输至船载主控模块，再将控制信号通过CAN 总线传输到驱动模块，对帆舵进行控制。

本次试验在中国海洋大学工程学院的人工湖内进行，平均水深1.2 m，水域面积较大，周围环境良好，用风速仪测得当天风力等级为5～6 级，环境条件适合本次无人帆船航行试验。无人帆船实物和湖面航行情况如图11 和图12 所示。

图13 所示为横风、逆风以及顺风这3 种常见帆船航行工况下，无人帆船利用速度选择LOS 法和速度选择法这2 种循迹方法的对比结果。由图可知：在横风（图13（a））与逆风（图13（b））工况下，2 种方法最终都可以到达期望位置，但速度选择LOS 法的轨迹（黑色实线）相对于速度选择法的轨迹（橘色实线）具有明显行程优势，更加贴合目标航线（蓝色虚线）。在顺风（图13（c））工况下，速度选择LOS 法相对速度选择法的优势不太明显，两者都可以到达期望位置。结果表明：速度选择LOS 法在实际应用中基本可以满足无人帆船的航行要求，且相对于速度选择法可以较好地贴合目标航线，证明该算法具有较高的可行性。

图 11 无人帆船实物图Fig. 11 Picture of the unmanned sailing boat

图 12 无人帆船湖面航行图Fig. 12 Lake trial of the unmanned sailing boat

图 13 横风、逆风和顺风工况下无人帆船试验结果Fig. 13 Lake trial results of the unmanned sailing boat in crosswind, headwind and tailwind conditions

5 结 语

本文提出了一种基于速度选择切换型LOS的无人帆船循迹航行控制算法，对无人帆船循迹航行进行了Matlab 仿真与湖上试验。对实船进行了等比例建模，通过速度预测模块获得了无人帆船每一个航向上的速度，并以速度极线图的形式进行了呈现。试验对比结果表明，在多变风向的情况下该算法优于单纯的速度选择法，切换型LOS 有效克服了无人帆船在水面航行时由于风、浪、流等因素所造成的航迹偏离影响，使偏航误差可以及时减小，并通过帆船的速度极线图获取最佳速度，从而快速到达期望点。本文研究结果对无人帆船智能循迹航行具有一定参考价值。