基于离散傅里叶变换的多旋翼无人机循迹检测系统设计

闵小翠，朱 君，李 鹏,2，周益全

(1.广州华立科技职业学院 计算机信息工程学院，广州 511325;2.华南理工大学 计算机科学与工程学院，广州 511325)

0 引言

无人机作为无线信息通信技术、远程控制技术、空气动力学技术等多学科快速发展应用下的综合性产物，已经广泛应用于工业生产、农业生产、地质勘探以及国防安保等多个领域。其主要应用价值在于无人操控的精准性。无人操控解决了作业环境条件对人员的限制，通过高精度控制，完成目标任务的操作。其中，无人机飞行轨迹的循迹功能，能够使无人机根据环境变量关系[1]，自主学习、分析环境物体关系[2]，自行寻找最优飞行线路。在循迹过程中，图像。坐标等数据的识别精度是决定循迹效果的关键。

根据对现有不同旋翼无人机循迹检测系统的作业日志分析发现，随着旋翼数量的增加，传统多旋翼无人机循迹检测系统的循迹数据开放聚合程度越高。不同传感器异步数据所产生的不对称数据，在很大程度上降低了循迹检测系统的检测效率，导致无人机在空中悬停时间过长，电量判断异常无法成功返航等循迹相关问题。为了解决开放聚合方案在传统多旋翼无人机循迹检测系统上出现的问题，有必要提出一种新的多旋翼循迹检测系统，从根源上解决上述问题。

1 基于离散傅里叶变换的多旋翼无人机循迹检测系统总框架设计

基于离散傅里叶变换的多旋翼无人机循迹检测系统总框架设计如图1所示，总共分为两个部分：

图1 基于离散傅里叶变换的多旋翼无人机循迹检测系统总框架设计示意图

1)基于离散傅里叶变换的多旋翼无人机循迹数据变换算力支持硬件，主要通过多路传感器信息采集控制主控，对多旋翼无人机轨迹进行数据综合分析，利用基于傅里叶变换计算架构设计处理器，配合多路数据离散电路，对开环数据进行闭环数据转换处理。其中主要依托外部接入的远端大型云服务器提供数据离散转换过程中需要的浮点计算能力。设计硬件功能侧重点在于数据的采集与转换过程中计算数据的本地数据化处理。为软件算法以及程序代码运行提供硬件平台。

2)基于离散傅里叶变换的多旋翼无人机循迹数据变换计算程序，即设计系统的算法执行软件。根据设计软件程序的作用面，可分为数据离散处理程序与循迹数据傅里叶变换输出程序两部分。通过两组程序的功能设计，实现在硬件数据资源与算力的支持下，将多旋翼无人机循迹数据相关参量由聚合形态，经离散傅里叶变换计算，转换为闭环数据处理形态[3-4]，从而优化循迹数据识别精准度，提升系统对循迹任务的整体效果。

2 基于离散傅里叶变换的多旋翼无人机循迹检测系统硬件结构设计

多旋翼无人机循迹数据采集硬件包括：数据传感器、数据逻辑变阻器与信号分量控制器；在功能实现过程中，首先通过RX5403数据传感器对多旋翼无人机多路传感器数据进行数据接口链路对接，然后由AD4431数据采集控制器通过对接链路采集无人机轨迹数据，并将数据传输至数据逻辑变阻器进行离散前的信号电路值变换，以此完成离散处理设备工作，最后由信号分量控制器调制输出。多旋翼无人机循迹数据采集硬件设计结构，如图2所示。

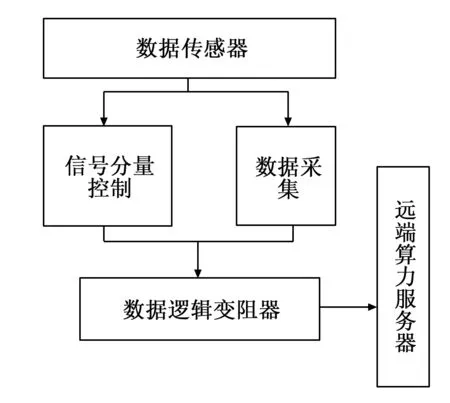
图2 多旋翼无人机循迹数据采集硬件设计结构

2.1 数据传感器

通过RX5403数据传感器对多旋翼无人机多路传感器数据进行数据接口链路对接，RX5403数据传感器包括采集系统、检测元件、转换电路。检测元件可分为光栅尺和直线感应同步器。这种检测元件具有很强的无线传输能力。RX5403数据传感器的传输速率可以达到3 Mbps。设定输出功率和频率后，就可以很好地完成信号的发送和无线交互收发。

2.2 数据逻辑变阻器

选用B722 系列变阻器作为系统硬件的数据逻辑变阻器。它具有允许工作温度较高，宽额定电压范围较大的特点，过数据逻辑变阻器进行离散前信号电路值变换，包含一组信号差量运算，算式如下所示:

(1)

其中:Δζ代表设计硬件的离散数据采集变量，L1、L2、L3分别是控制量、采集量、离散量的硬件预置系数，上述参数为B722 系列变阻器的系统预制参数。

2.3 信号分量控制器

在大多数情况下，信号适调是由具有一种或多种信号适调功能的独立仪器单元及其组合完成的。但是，随着技术的发展，一部分信号适调功能并入传感器中，而另一部分信号适调功能并入数据记录仪器或数据采集与记录仪器系统。信号适调器主要采用两种前置放大器：电压放大器和电荷放大器。在多旋翼无人机循迹检测系统硬件结构中，信号GL827L适调器是检测系统的重要组成部分。传感器的输出信号均需要经过适调，以系统传输的要求。信号适调器主要包括信号变换器、放大器、滤波器、微分器和积分器及电源。

3 基于离散傅里叶变换的多旋翼无人机循迹检测系统软件设计

3.1 数据离散处理程序设计

考虑到多旋翼无人机不同传感器信号同步存在一定量的误差，因此在循迹过程中需要与不同旋翼数据进行数据对称，以此提升循迹数据识别处理的精准度。基于上述思想，需要对统一的数据处理结构进行离散处理，利用设计硬件的算力基础条件，配合数据离散处理程序，完成对多旋翼无人机循迹数据的离散处理。设计程序原理与实现过程如下：

首先对无人机不同传感器反馈的轨迹数据信息进行权值与阈值关系梳理优化。通过梳理将多旋翼无人机反馈数据的权值与阈值转换为实数量值，并对其量值的赋予，赋予值范围定义为0～1[5]之间的任意数。然后，通过离散算法来实现对数据结构的离散转换输出。在此之前，需要将无人机循迹数据网络对应的函数进行离散激活，使其满足S型函数条件[6]，然后通过离散数据构成与数据特征，获得不同类型数据所对应的最佳循迹特征，从而减小不同传感器反馈循迹数据之间的均方差。程序功能实现的函数表达方式如下：

(2)

式中，yz,w，代表第w个传感器反馈的第z个循迹数据量；Uz,w代表第w个传感器反馈的第z个离散值；f代表载入旋翼反馈数据总量；d代表程序调用算法的总线程数量。下面是数据离散处理程序算法实现的伪代码示例:

category.msgbus=WARN/Win32DbgAppender, ConsoleAppender//离散/open

log4j/.categor/TBarBiz=WARN/

Win32DbgAppender/ConsoleAppender/TBarBizFileAppender*

log4j.category/TBarMsgMgr=WARN

Win32DbgAppender//ConsoleAppender/ TBarMsgMgrFileAppender

log4j.category.IMWebBridge=INFO/

/

Win32DbgAppender/ConsoleAppender*

IMWebBridgeFileAppender

log4j.additivity.SdkRender=FALSE

#log4j.additivity.msgbus=5

#log4j.additivity.TBarBiz=FALSE

#log4j.additivity.TBarMsgMgr=1

log4j.additivity/ChatMsgMgr=FALSE

log4j.additivity/IMWebBridge=0

#log4j/additivity/Http=FALSE

Log5/appender.Win32DbgAppender=org.apache/log4j/Win32DebugAppender

log4j.appender.Win32DbgAppender.layout.ConversionPattern=%d{} %p %c %m%n

log4j.appender.ConsoleAppender.layout.ConversionPattern=%d{} %p %c %m%n

数据离散处理程序功能实现流程，如图3所示。

图3 数据离散处理程序功能实现流程

通过上述对不同旋翼反馈循迹数据的离散计算后，程序将得到一组循迹轨迹的IMF分量数据[7]，通常情况下，分量数据由6阶函数构成[8]，因此将其定义为6阶IMF分量数据。根据分量数据可得到不同分量对旋翼移动轨迹的坐标、高度、气压等循迹相关指数信息，为了保证设计系统最终循迹输出结果的精准满足0.5 m级精度，将获得分量定义为下级傅里叶变换计算的样本数据。具体定义实现流程如图4所示。

图4 离散分量样本化转换实现过程

3.2 循迹数据傅里叶变换输出程序设计

完成对多旋翼无人机循迹数据的离散程序设计后，对系统循迹数据傅里叶变换程序进行设计。程序设计主要目的在于对离散数据传输通道内的回路进行闭环转换，防止开环通道的聚合特性[9-11]引入冗余数据，干扰精准数据离散循迹特征的对比识别。从而保证输出的循迹检测结果的精准度[12-14]。

ty代表离散循迹信号。离散后的信号隶属于正弦零均值信号，对其进行变换权值系数的赋予权限并输出。

循迹数据傅里叶变换输出程序闭环变换功能实现分为以下 3 个步骤：

1)对载入的离散循迹信号o0进行傅里叶信号振荡，振荡后得到傅里叶变换信号o0g，对载入离散循迹信号的振荡频率与幅值进行计算[15-18]。

(3)

式中，s0、sl、ml代表傅里叶系数，ξ代表程序变换过程中载入的预置角频率。

2)在计算环境中释放一个小幅值、频率一致的测试信号tv，利用测试信号获得循迹信号测试载入接口与识别输出接口之间的数据精度相位差与优化比[19-21]。

tv=Svsin(ξy+φv)

(4)

式中，对幅值Sv取值范围设置为15%～25%；最大化匹配相近的循迹数据相位φv，保证振荡信号在变换过程中的精度损失最小。将变换后的数据信号进行输出前的二次傅里叶变换，可得到：

(5)

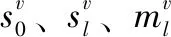
od=Sdsin(ξy+φs)

(6)

由此程序可通过变换计算获得相位差φdv=φd-φv与增益比i=Sd/Sv两组变换核心数据量。

3)进一步，程序可通过相位差计算，获得优化后的循迹数据识别输出信号为：

(7)

4 对比实验

对设计的基于离散傅里叶变换的多旋翼无人机循迹检测系统多旋翼无人机循迹效率进行对比实验。

4.1 实验设计

实验采用对比方式来进行，实验共分为两个部分，分别为多旋翼无人机循迹检测精度对比实验与多旋翼无人机循迹检测响应对比实验，然后通过多旋翼无人机循迹效率公式计算得出实验系统的循迹效率，根据效率值得出实验结论。

具体实验步骤如下：

1)利用X86架构计算与Windows平台构建测试环境，并将设计系统接入测试环境，同时引入传统无人机循迹检测系统作为对比实验系统；

2)在测试环境中导入一组常规型多旋翼无人机飞行数据；

3)分别由设计系统与传统检测系统进行循迹数据的精度检测，数据采用随机抽取的方式获得。抽取样本数据量为10；

4)对比数据得出小结实验结论；

5)在相同环境条件下，分别获取设计系统与传统检测系统循迹数据的响应数据；

6)对比数据得出小结实验结论；

7)根据无人机循迹效率公式计算得出实验系统的循迹效率；

对比效率值，得出最终实验结论。

4.2 设计系统与传统多旋翼无人机循迹检测系统循迹检测精度对比实验

根据上述4.1实验步骤，得到设计系统与传统多旋翼无人机循迹检测系统循迹检测精度对比结果，如表1所示。

表1 设计系统与传统多旋翼无人机循迹检测系统

通过对比表1中的实验结果发现，提出设计的系统能够将无人机轨迹数据检测识别误差控制在0.010～0.090 m范围内，在循迹检测误差实量转换下的误差控制范围小于0.1 m；相比之下，传统多旋翼无人机循迹检测系统的无人机国际数据检测识别误差范围较大，且不稳定；基于上述数据对比，可证明设计系统具有改善循迹检测精度的效果。

4.3 设计系统与传统多旋翼无人机循迹检测系统循迹检测响应对比实验

根据上述4.1实验步骤，得到设计系统与传统多旋翼无人机循迹检测系统循迹检测响应对比结果，如表2所示。

表2 设计系统与传统多旋翼无人机循迹检测系统

通过表2实验结果对比发现，提出设计的基于离散傅里叶变换的多旋翼无人机循迹检测系统，在循迹检测响应时间上，明显快于传统多旋翼无人机循迹检测系统，且响应时间毫秒值提升效果明显，由此可证，在此次实验中，设计的基于离散傅里叶变换的多旋翼无人机循迹检测系统通过了多旋翼无人机循迹检测响应测试。

4.4 循迹检测效率数据计算

对上述两组实验中表1、表2的结果数据进行多旋翼无人机循迹检测效率计算，通过计算获得设计系统与传统多旋翼无人机循迹检测系统的检测效率，计算公式如下：

(8)

式中，F代表多旋翼无人机循迹检测效率；Q代表多旋翼无人机循迹检测精度；T代表多旋翼无人机循迹检测响应系数。根据公式得到计算后的设计系统与传统多旋翼无人机循迹检测系统的检测效率，如表3所示。

表3 设计系统与传统多旋翼无人机循迹

4.5 综合实验结论

综上所述，根据表3计算结果可以看出，提出设计基于离散傅里叶变换的多旋翼无人机循迹检测系统，循迹检测整体效率较传统多旋翼无人机循迹检测效率提升效果明显。由此可以证明，提出设计的基于离散傅里叶变换的多旋翼无人机循迹检测系统，满足设计与实际应用要求，具有较高的推广性与应用性。

5 结束语

文章对传统多旋翼无人机循迹检测系统存在的问题进行了深入研究，针对性提出了基于离散傅里叶变换的多旋翼无人机循迹检测系统设计，并对设计系统的硬件与软件功能、结构进行了详细描述。通过对比实验数据证明了提出设计的有效性。基于离散傅里叶变换的多旋翼无人机循迹检测系统设计的提出与完成，为无人机循迹研究与应用，提供了新的研究思路与应用解决方案。