太赫兹波计算鬼成像：原理和展望

2020-06-02陈思潮杜良辉朱礼国

光电工程 2020年5期

陈思潮，杜良辉，朱礼国*

太赫兹波计算鬼成像：原理和展望

陈思潮1,2，杜良辉1,3，朱礼国1,3*

1中国工程物理研究院流体物理研究所，四川绵阳 621900；2中国科学技术大学光学与光学工程系，安徽合肥 230026；3中国工程物理研究院微系统与太赫兹研究中心，四川成都 610200

本文立足于太赫兹波成像领域近年来备受关注的研究热点—太赫兹波计算鬼成像，首先回顾了鬼成像从量子到经典再到计算的历史过程，然后阐述了计算鬼成像的数学原理，随后综述了计算鬼成像在太赫兹波段的发展历程，及其在超衍射分辨成像、石墨烯光电导成像、太赫兹光谱成像等方面的应用，并在最后展望了太赫兹波计算鬼成像的发展前景：计算鬼成像作为一种成像手段，可以绕开在太赫兹频段缺乏经济高效的焦面阵列式探测器的难题，但目前的成像帧率还难以满足快速成像的应用需求，相信在未来随着器件性能的提升和成像算法的优化，其成像帧率可以得到大幅提升。

鬼成像；单像素成像；关联成像；太赫兹波

1 引言

1.1 鬼成像技术的发展

与传统的采用焦面像阵(focal-plane array, FPA，比如CCD相机等)成像方式不同，鬼成像(ghost imaging, GI)是通过光场的关联运算(或称符合运算)来获得物体的空间或相位分布，故又称为关联成像(correlated imaging)或符合成像(coincidence imaging)。回顾鬼成像发展历程，可总结为量子鬼成像、经典鬼成像、计算鬼成像等三个过程[1]。

鬼成像的历史最早可以追溯到1956年，Hanbury Brown和Twiss提出将光场的二阶关联(强度)应用到遥远天体(天狼星)的角直径测量[2-3]，为关联成像技术的发展奠定了基础。

1995年，Maryland大学的Pittman等人[4]利用纠缠光子对，首次在实验上实现了量子鬼成像，其实验装置如图1(a)所示。他们利用自发参量下转换(spontaneous parametric down-conversion, SPDC)制备了两路正交偏振的纠缠光子对，其中一路称为信号光(signal beam)，用来照明目标，其光强值最终被没有空间分辨率的探测器探测并记录；另外一路称为闲置光(idler beam)，不经过成像目标，其空间光强分布被具有空间分辨能力的探测器探测并记录。当对两路光子进行关联计数时，实验人员成功地获得了目标的空间图像。

Boston大学的Abouraddy等人[5]分析认为鬼成像是利用量子效应实现的，纠缠光子作为光源在鬼成像技术中扮演了不可或缺的角色。然而在2002年，Rochester大学的Bennink等人[6]用氦氖激光器作为光源，利用一片旋转的毛玻璃对光场引入随机的扰动，仍然实现了对目标的鬼成像(图1(b))，从而将鬼成像技术推广到基于经典相干光源的应用场景。

但是，无论量子鬼成像或者经典鬼成像在对目标进行关联测量时，都需要搭建测量光路(test arm)和参考光路(reference arm)，并需要给两个光路都配备探测器，这在一定程度上增加了成像系统的复杂度。2008年，麻省理工(MIT)的Shapiro发表了名为“Computational ghost imaging”的文章[7]，从理论上提出了仅需要一路测量光路同时配备一个单像素探测器(single-pixel detector)实现鬼成像的方案。该方案如图1(c)所示，需要用到空间光调制器(spatial light modulator, SLM)按照预设生成随机起伏的光强图案(掩膜版)来照明目标，以代替参考光路在传统鬼成像中起到的关联作用。同年，Rice大学的Duarte等人[8]利用一种振幅型的空间光调制器¾数字微镜阵列(digital micromirror device, DMD)，独自从实验上实现了对目标的计算鬼成像，由于该方案使用到的唯一探测器不具有空间分辨能力，所以该课题组又称这种方式为单像素成像(single-pixel imaging)。

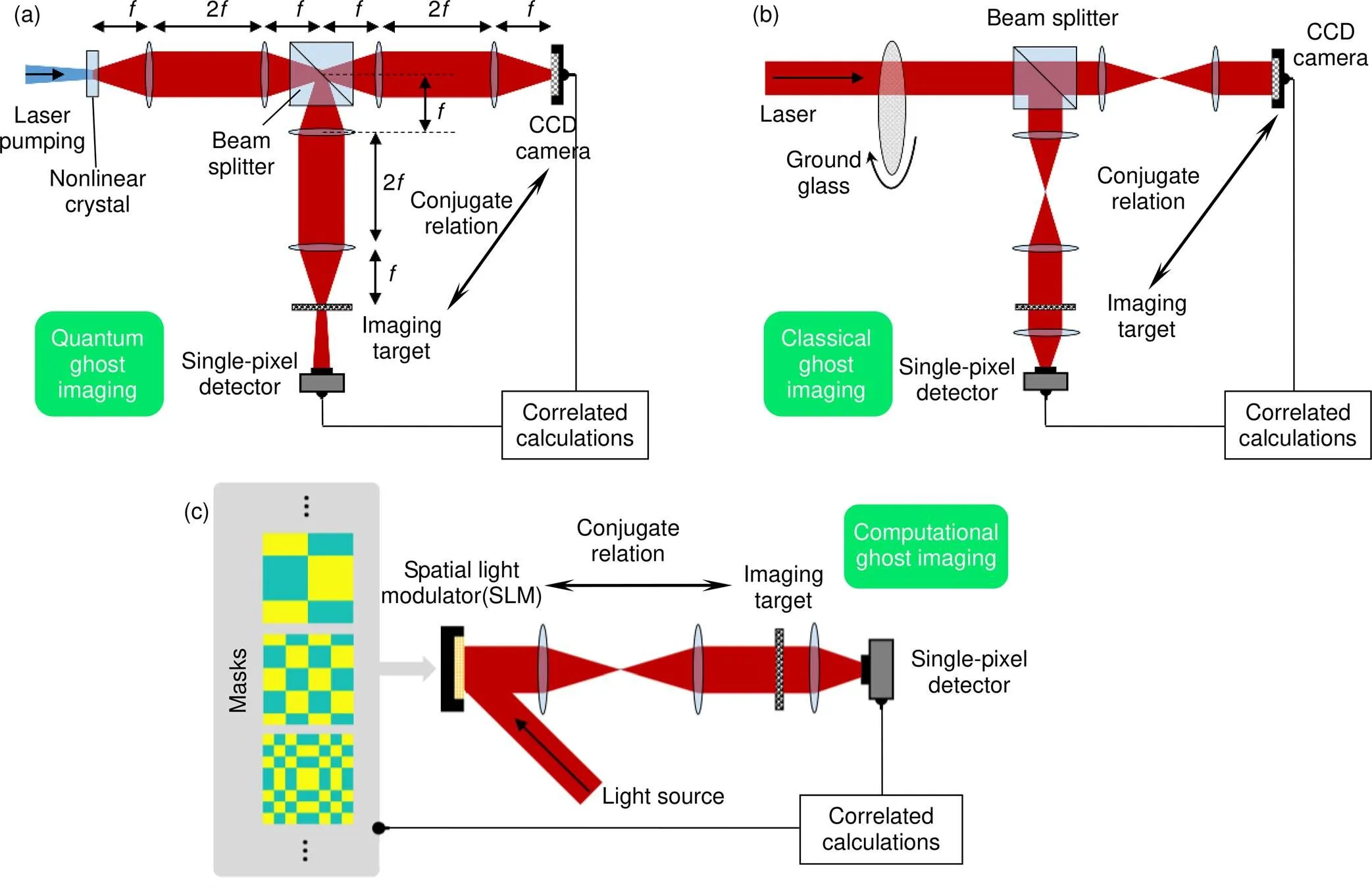
图1 (a) 量子鬼成像示意图；(b) 经典鬼成像示意图；(c) 计算鬼成像示意图

然而，与传统的FPA成像方式相比，鬼成像的本质是在时间序列上对关联光场光强随机涨落的采样统计，所以存在成像时间较长的弊端。而就在计算鬼成像被首次提出的两年前，即2006年，三位数学家Tao，Candes和David共同提出[9-11]一种新的图像压缩采样理论¾压缩感知(compressive sensing，也称为compressive sampling)，它基于图像的稀疏特性，允许在大幅减少采样次数的同时恢复出高保真度的图像。该理论要求的采样过程与计算鬼成像的成像原理十分契合，很快就被实际应用到了计算鬼成像之中[8, 12]，这使得鬼成像的速度得到了大幅提升。

1.2 鬼成像技术的比较

如上文所述，鬼成像技术经历了量子鬼成像到经典鬼成像再到计算鬼成像等三个重要发展阶段。在2004年，Bennink等人[13]指出，根据傅里叶理论，用经典光源获取的图像必须满足关系ΔΔ≥1，其中Δ和Δ分别表示关联图像在像空间和傅里叶空间的分辨率。他们通过改变鬼成像系统中透镜的位置，利用经典光源，依次在像平面和傅里叶平面获得了目标的经典关联图像，此时获得的ΔΔ=1.5。当他们用纠缠光子(参量下转换)对目标进行量子鬼成像时，得到的实验结果ΔΔ=0.35±0.15，证明了量子鬼图像的分辨率积与经典衍射理论相比提高了三倍。根据Bennink等人的分析，在量子鬼成像中所用的纠缠光子比经典相干光源具有更好的关联特性，量子鬼图像相较于经典鬼图像，具有更高的对比度和空间分辨率。但同时，纠缠光源的制备难度高，且容易受外界噪声影响，所以量子鬼成像对成像环境的要求较高，应用范围也相应地受到一定的限制。

而利用经典光源实现鬼成像，虽然其图像质量与量子鬼成像相比相对差一些，但是光源更容易获得的，具有更广阔的应用场景。在2009年，中国科学院的韩申生研究员课题组[14]在经典鬼成像的实验架构上也实现了超越经典衍射极限的成像分辨率。为了直观地比较鬼成像与传统成像方式在分辨率上的差别，他们将常规鬼成像系统中的测量光路设计为一个成像光路，用CCD相机代替单像素探测器以直接获取目标的传统图像，同时，将CCD获取的总强度值(对图像做面积分)与参考光路测得光场分布做二阶关联可获得目标的鬼图像。对于传统图像，其分辨率受限于衍射极限，即Δ0=0.61/T，其中为照明光源波长，T表示测量光路里光学系统的数值孔径；而对于鬼图像，根据对整个衍射受限系统脉冲响应函数的分析，韩等人从理论上得出其分辨率为ΔG=0.61/(T2+R2)1/2，其中R表示参考光路里光学系统的数值孔径。该结果表明，利用光场的二阶关联计算出的鬼图像，其空间分辨性能会因为参考光路而提升，具体地，与测量光路的衍射极限相比，其空间分辨性能可以提高[1+(R/T)2]1/2。他们用倍频的Nd:YAG脉冲激光(=0.532 μm)对狭缝(缝宽20 μm，狭缝中心相距40 μm)做了成像实验，实验系统的Δ0≈40.1 μm(T=0.008)，用CCD直接获取的传统图像处于恰可分辨的状态，而通过光场二阶关联获得的鬼图像的分辨率得到明显提升，并且随着R的增加(增大参考光路的通光孔径)，相应鬼图像的空间分辨率也越精细，实验结果和理论预测定量符合得很好。

而随后在经典鬼成像的基础上发展起来的计算鬼成像，由于只需要一路测量光路，简化了成像系统的同时，也不再需要对光源有相干性的要求。计算鬼成像所获得的空间分辨率由掩膜版与目标关联作用时掩膜光场的精度决定，由于计算鬼成像可以较为方便地把目标放置在掩膜光场的近场范围之内，在这种情况下可以大幅打破衍射极限，获得分辨率极精细的图像。此外，计算鬼成像可以方便地与压缩感知理论相结合，在保证相当的图像保真度的情况下大幅提高成像速度。正是由于计算鬼成像的这些特性，近年来在太赫兹成像方面，计算鬼成像得到了越来越多的应用。

2 计算鬼成像的原理

2.1 计算鬼成像的数学描述

如图2(a)所示，计算鬼成像在第次关联测量中，需要用一个大小为×的掩膜版对光源进行空间调制，以获得对应空间分布的结构光。空间编码的结构光随后照明成像目标并携带了目标空间信息，最终结构光强度被没有空间分辨能力的单像素探测器探测并记录。

我们可以假设将成像目标(连续图像)在空间上离散为大小也为×的数字图像m，该矩阵的像素与掩膜版的单元在空间上一一对应，那么探测到的光强就可以表示为

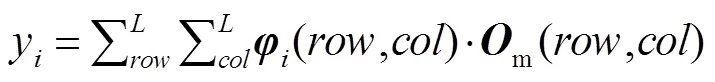
其中：和分别表示掩膜版单元(图像矩阵像素)所在的行数和列数。如果将矩阵和m按照行(或者列)重新排列成长度为=×的向量和，那么式(1)可以方便地写为两个向量的内积：

其中表示元素在向量中的位置。

现在考虑有个线性无关的掩膜行向量1，2，…，，将它们按列方向组成一个大小为×的方阵，称为观测矩阵。那么，如图2(b)所示，对成像目标的整个关联测量过程就可以被表示为

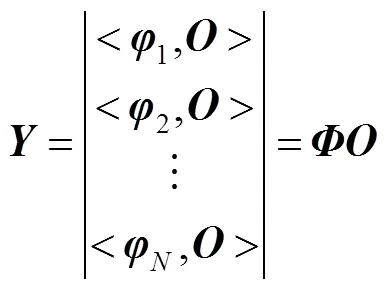
其中：是由关联测量值组成的列向量，其长度为，如图2(c)所示。而由于要求这个掩膜向量都是线性无关，即观测矩阵一定存在逆矩阵-1，那么便可以根据下式重构出目标图像：

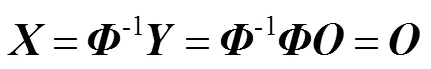
2.2 不同观测矩阵在噪声环境中的特性

在理想情况下，只要观测矩阵可逆，便可以通过式(4)精确地恢复出图像。但在实际情况下，由于噪声的存在，式(3)应写为

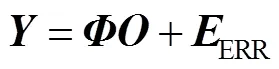
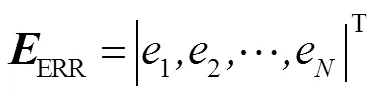
那么式(4)便写为

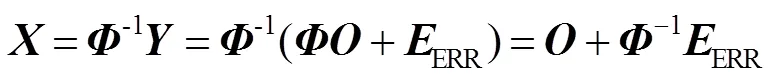
用均方根误差(root mean square error，RMSE，用RMS表示)来描述重构图像与目标图像的差别：

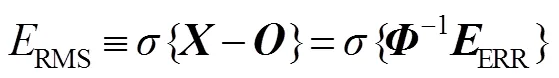
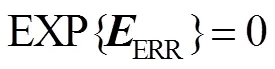
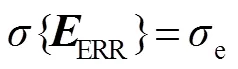
那么，可以证明[15]，式(8)可写为

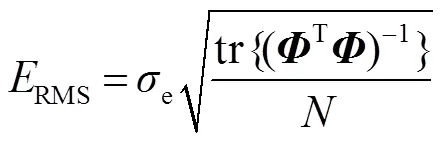
其中tr表示对括号内的矩阵求迹。常用的观测矩阵有扫描矩阵，随机矩阵n，余弦矩阵和Hadamard矩阵等(如图3(a))。而Harwit和Sloane证明了[15]观测矩阵满足不等式：

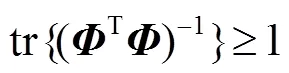
并且，当且仅当观测矩阵为时，式(12)取最小值1。图3(b)所示为相同噪声情况下，不同观测矩阵重构图像的计算仿真结果。

3 计算鬼成像在太赫兹波段的应用

太赫兹(1 THz=1012Hz)波通常指频率处于0.1 THz~10 THz间的电磁辐射(对应波长3 mm~30 μm)，在过去相当长的一段时间里，由于缺乏有效的太赫兹源与探测器件，这一波段一直没有得到广泛的应用而被称为“太赫兹间隙”。而20世纪80年代以来，得益于超快光电子技术与半导体技术的发展，太赫兹科学与技术获得了越来越广泛的关注并取得了飞速的发展。

太赫兹波由于其诸多独特的性质[16]，在许多领域都有着广泛的应用前景：1) 太赫兹波的光子能量很低(1 THz，4 meV)，是一种非电离辐射，在辐照剂量不引起可观热效应的前提下，太赫兹辐射对生物是相对安全的，可以应用于生物医学的研究[17-19]。2) 太赫兹波在诸如塑料、纸张、陶瓷等极性材料中有很高的透过率，可以应用于无损检测[20]。3) 许多大分子在太赫兹频段有本征吸收峰，利用这种指纹谱特性可以实现物质的特异性传感[21]。4) 水分子在太赫兹波段有较强的吸收[22]，利用该项特性可以用来区分不同含水量的生物组织[23]。5) 与毫米波相比，太赫兹波带宽更宽，可实现更高速的无线通讯[24-25]，是未来实现6G通讯的基础。6) 太赫兹时域光谱技术能够提供高信噪比，宽频谱，亚皮秒量级时间分辨率的信号，是研究材料科学的有效手段，再结合相干光泵浦，可以应用于载流子动力学[26]，材料相变过程[27-29]的研究。

图3 常用观测矩阵及其在噪声环境下的鬼成像仿真结果

Fig. 3 The common observation matrix and simulation results of ghost imaging in noisy environment

基于上述性质，太赫兹成像也有巨大的应用前景，在多个领域实现了诸如无损检测[30]、化学成像(chemical mapping)[31]、生物检测[32]、肿瘤成像[23]等应用。但是在太赫兹波段，由于性能优越的阵列式探测器制造比较困难，以往的太赫兹成像通常采用逐点扫描的方式。而将鬼成像与太赫兹成像相结合，是避开以上难题的有效途径。

3.1 太赫兹计算鬼成像的首次实现

在2008年，美国Rice大学的Chan等人[33]利用印刷电路板(printed-circuit boards, PCB)技术制作了600个随机掩膜版(掩膜单元数量为32×32，尺寸为1 mm)，利用光电导天线(photoconductive antenna，PCA)产生太赫兹辐射，首次在太赫兹波段(0.1 THz，0=3 mm)实现了压缩感知(采样率为60%)的计算鬼成像，如图4所示。Chan等人的工作为太赫兹成像开辟了新的技术路线，但同时，这种采用难以重构的“固态”的PCB作为掩膜版的方案存在许多缺点。首先，在成像之前需要预先制备大量的PCB掩膜版；其次，在成像过程中这些PCB掩膜版的机械切换速度会大大制约该系统的成像速度；此外，PCB掩膜版一旦制备完成，系统成像参数(比如像素大小、视场等)便难以灵活调节。

图4 莱斯大学实现太赫兹波段计算鬼成像。(a) 实验示意图；(b)∼(d) 鬼成像结果[33]。(b) 为成像目标的光学图像，(c)和(d)分别是采样率为30%和60%情况下的，基于最小变分法重构的压缩图像(0.1 THz)，像素大小为1 mm，像素阵列为32×32

Fig. 4 First demonstration of THz computational ghost imaging[33]. (a) Schematic of the THz computational ghost imaging;(b) The photography of the imaging target; The compressive THz ghost images with sample ratio of 30% (c) and 60% (d)

3.2 动态可重构的空间太赫兹调制器

2013年，Boston学院的Padilla课题组[34]为了克服“固态”掩膜版的缺点，提出利用空间编码的红外光泵浦高阻硅(silicon, Si)以实现动态可重构的空间太赫兹波调制器(spatial THz wave modulator, STWM)，进而实现太赫兹波的计算鬼成像。如图5所示，他们利用DMD对980 nm的红外光按照掩膜版进行空间调制，空间编码的红外光投影到高阻Si表面，会激发高阻Si内部产生相应空间分布的光生载流子，从而处于光泵浦区域的Si对太赫兹辐射的吸收也会增加，以此实现对太赫兹辐射的动态可重构的空间掩膜效果。该方案不再需要制备“固态”的掩膜版，而仅需预先把掩膜图案通过电脑输入到DMD的存储器上，目前商用DMD最快的调制速度能达到20 kHz，而且系统的成像参数可以通过光学系统灵活地调节。然而，该方案使用连续光源泵浦，在光电导材料Si中存在光生载流子扩散的问题，导致其掩膜单元(像素)的边缘是弥散的，无法应用于高分辨率甚至超衍射分辨的太赫兹鬼成像。

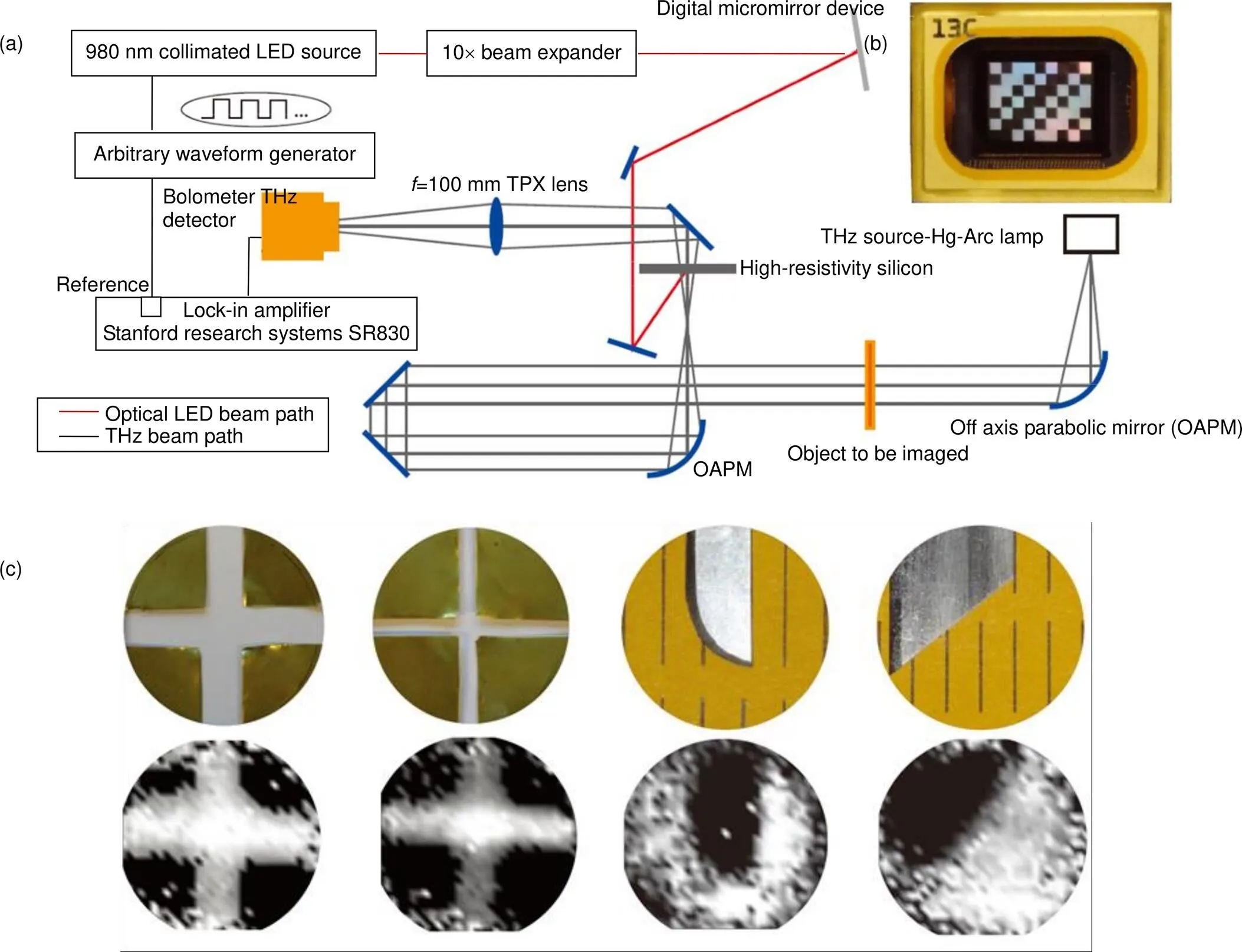
图5 Padilla团队利用动态可重构的STWM实现太赫兹计算鬼成像[34]。(a) 实验示意图；(b) DMD光学照片；(c) 成像目标光学照片(上)及相应的太赫兹计算鬼成像结果(下)

2014年[35]，Padilla团队也提出了一种基于“固态”的、动态可重构的STWM来实现太赫兹波段的计算鬼成像。他们利用工作在太赫兹波段的超材料完美电磁波吸收器(metamaterial absorbers，MMA)[36]组成一个8×8的阵列(阵列中每个单元包含18×18个MMA，单元面积为600 μm×600 μm)。当对阵列里任一单元施加偏置电压时(15 V)，其太赫兹波段的吸收谱会发生显著的变化，利用这一差异，便可以对这64个单元实现单独的空间动态操作。最终，他们利用这个“固态”的、动态可重构的STWM在太赫兹波段成功实现了对目标的计算鬼成像。不过，该方案由于掩膜单元尺寸较大，也难以满足超衍射分辨的太赫兹鬼成像需求。

3.3 超衍射分辨的太赫兹计算鬼成像

在传统的太赫兹成像中，由于受到衍射极限的制约，其空间分辨率很难突破亚毫米量级(1 THz~300 μm)，这大大制约了太赫兹波在微观领域的研究。近年来，有研究人员将近场感知理论与计算鬼成像相结合，成功实现了太赫兹波的超衍射分辨成像。

2016年[37]，英国Exeter大学的Hendry课题组在Padilla的工作基础上，采用相干的光泵浦/太赫兹探测系统来解决连续光泵浦所带来的载流子扩散问题，同时，他们将成像目标置于太赫兹掩膜的近场范围，首次实现了超衍射分辨的太赫兹波计算鬼成像，获得的太赫兹图像空间分辨率为103 μm±7 μm(~0/4，太赫兹脉冲中心波长0=375 μm)。他们利用飞秒激光脉冲(中心波长800 nm，重频1050 Hz)泵浦高阻Si，通过控制光路中的时间延迟线，太赫兹脉冲到达Si表面的时间被精确地设置到Si被光激发5 ps之后，而此时载流子的扩散可以忽略不计。该工作用的Si片厚度仅有115 μm，他们把成像目标贴在Si片光激发面的背面，使结构太赫兹波在近场感知成像目标，最终打破衍射极限，实现了~0/4空间分辨率的太赫兹波计算鬼成像(如图6所示)。

由于携带高频空间信息的倏逝波随传播距离是呈指数衰减的，所以要想获得更高的空间分辨率便需要缩短太赫兹掩膜与目标间的距离。次年[38]，同一课题组将Si片厚度缩减为6 μm，进一步将太赫兹图像的空间分辨率提高到9 μm±7 μm(~0/45)。同时，他们还结合了压缩自适应计算鬼成像[39]算法，用35%的采样率(采样数除以Nyquist采样极限)清晰地获得了目标图像，并且，他们还将该方法与常用的压缩感知算法相比，发现在相同采样率下，自适应算法表现出了更好的成像效果。

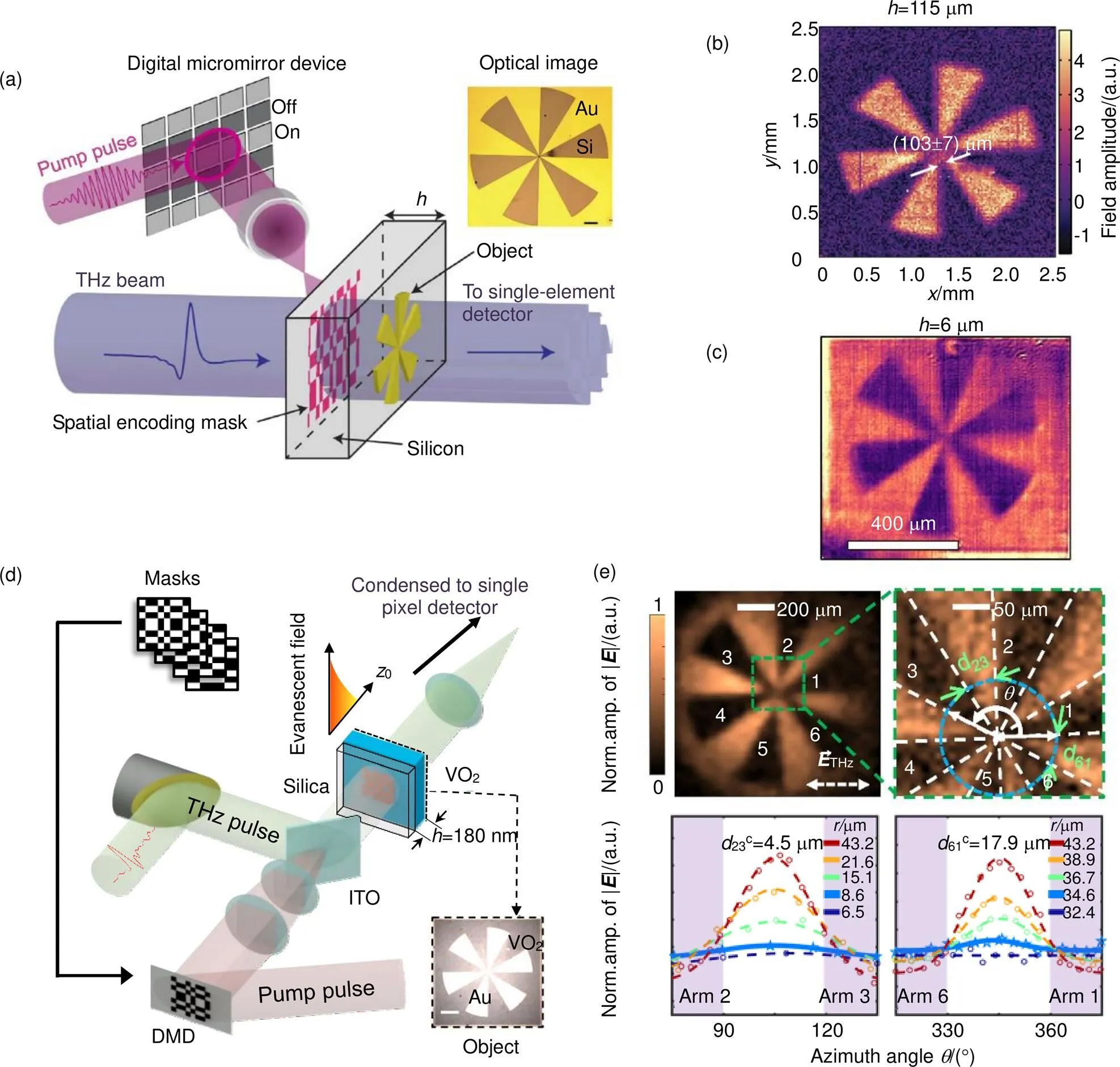
图6 超衍射极限分辨的太赫兹计算鬼成像。(a) 基于空间光泵浦Si的实验示意图；(b), (c) 在Si片厚度分别为115 μm[37]和6 μm[38]时的太赫兹超分辨计算鬼成像结果；(d), (e) 分别是基于空间光泵浦VO2的实验示意图及其太赫兹超分辨计算鬼成像结果[41]

但是由于800 nm激光在Si中的穿透深度为~12 μm[40]，如果进一步缩减Si的厚度，就会导致载流子数量下降，从而对太赫兹波的调制性能也会呈指数下降。2018年[41]，本课程组提出利用相变纳米薄膜材料二氧化钒[42](vanadium dioxide, VO2)的光致金属-绝缘相变[43](metal-to-insulator phase transition, MIT)特性，结合DMD空间编码的飞秒激光，实现对相干太赫兹脉冲高效的空间调制。同时，VO2薄膜厚度通常为~100 nm，在这一量级的近场区域理论上可以实现亚微米量级空间分辨率的太赫兹图像。最终，利用厚度为180 nm的VO2实现了4.5 μm空间分辨率的太赫兹波计算鬼成像，首次通过计算鬼成像的方法将空间分辨率提升到小于百分之一中心波长(0/133，0=600 μm)。

2019年[44]，美国Rochester大学的张希成教授提出另一种实现超衍射分辨的太赫兹计算鬼成像的方法。如图7(a)所示，他们将近场理论、计算鬼成像技术和电光采样技术三者相结合，将待测目标与电光晶体ZnTe紧贴，利用空间编码的探测光(800 nm)实现对携带目标高频信息的近场太赫兹倏逝波实现空间编码的探测，从而实现62 μm空间分辨的太赫兹计算鬼成像，其结果如图7(b)所示。张教授团队所提出的方法不需要再依赖特殊的空间太赫兹波调制器，同时，也因为该方案不再需要相干的泵浦光而具有更简化的光路系统。

3.4 石墨烯光电导分布的太赫兹计算鬼成像

光泵浦太赫兹探测系统是研究许多材料载流子动力学的重要手段，但在薄膜材料，尤其是诸如石墨烯等二维材料的制备过程中，材料的沉积在空间上很可能是不均一的，而通常的光泵浦太赫兹探测系统给出的都是在空间上平均后的结果，这便可能对材料性质的解读带来偏差。

2016年[45]，Hendry的课题组在光泵浦太赫兹探测系统的基础上，结合计算鬼成像的方法，成功获得了石墨烯在太赫兹波段的亚波长尺度的瞬态光电导分布图像，其结果如图8所示。

3.5 太赫兹光谱计算鬼成像

利用太赫兹波的指纹谱特性识别特异性物质是太赫兹成像的一个重大应用，这允许在获得目标形态学图像的同时，还能识别/分析目标的物质成分，其中的关键在于获取具有频谱信息的太赫兹图像。

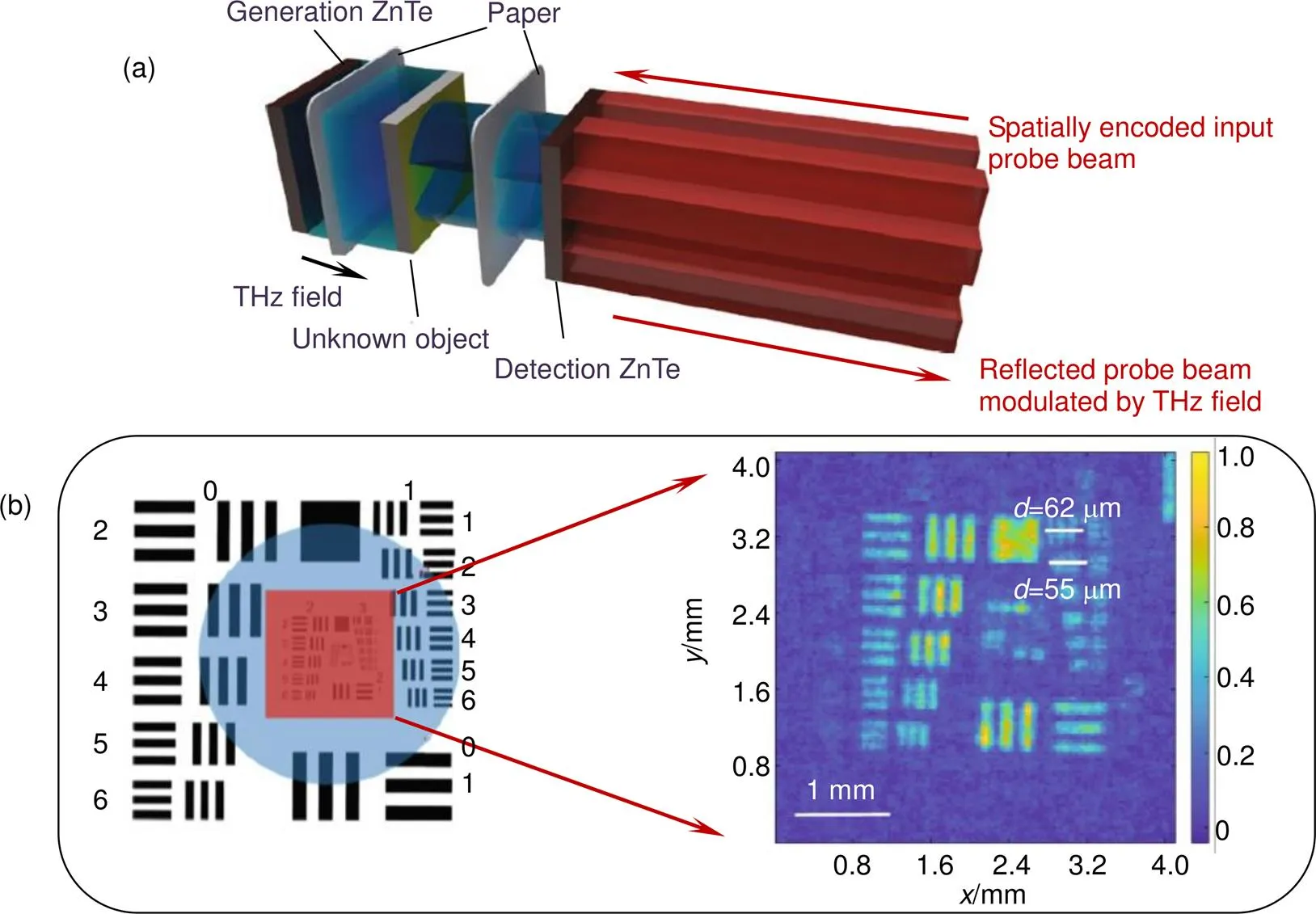
图7 空间采样以实现超衍射分辨的太赫兹波计算鬼成像[44]。(a) 采样方法示意图；(b) 成像目标示意(左)及太赫兹波成像实验结果(右)

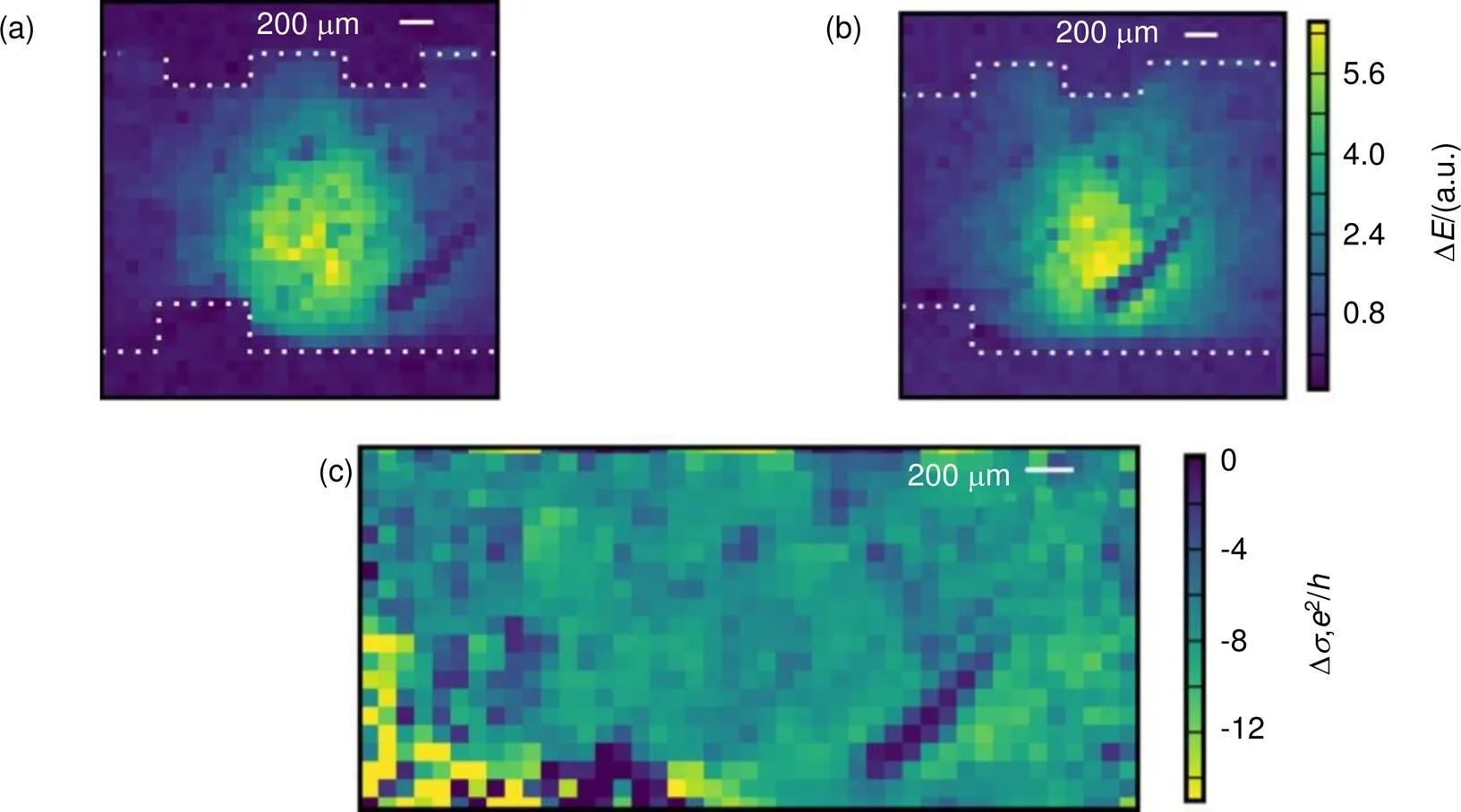
图8 石墨烯光电导分布的太赫兹计算鬼成像[45]。(a) 光泵浦石墨烯在某个视场下导致的太赫兹场透射场强变化空间分布ΔE；(b) 石墨烯横向移动了450 μm后的ΔE；(c) 计算出的石墨烯在太赫兹频段的光电导变化的空间分布Δσ。(a)~(c)中可以明显观察到石墨烯有一处缺陷

2018年，来自英国Sussex大学的Olivieri等人[46]提出了时间分辨的非线性鬼成像(time-resolved nonlinear ghost imaging, TNGI)技术以获取目标的太赫兹光谱图像。他们设计的技术方案利用空间光调制器形成空间编码的飞秒激光，用以激发非线性晶体(如ZnTe等)直接产生空间编码的太赫兹波辐射，随后结合太赫兹波照明后方目标和太赫兹时域光谱技术将透射太赫兹脉冲的时域波形记录下来，最终通过关联计算便可以获得某个延迟时刻所对应的太赫兹鬼图像，而其太赫兹光谱图像也可以通过傅里叶变换获得。他们将金、特氟龙(Teflon)、聚酰亚胺(Kapton)等三种材料制成的物体作为成像目标，用仿真的方法模拟了对该目标实现TNGI的过程，并获得了目标的太赫兹光谱图像，如图9所示。由于Kapton和Teflon在太赫兹频段有非常不同的频谱响应，在不同频点的太赫兹图像可以非常明显地区分出相应的物质。最近，Olivieri等人[47]给出了他们利用TNGI技术获得目标的太赫兹光谱图像的实验结果。需要指出的是，在TNGI技术中，计算鬼成像的关联测量是一个线性过程(如2.1节所述)，Olivieri等人所提出的“非线性”是指需要利用非线性晶体的光整流效应来产生空间编码的太赫兹脉冲。

4 前景展望

将计算鬼成像的方法应用到太赫兹波成像中，回避了太赫兹波段的焦阵面式探测器难以获得的困难，开辟了新的太赫兹成像手段。从太赫兹波计算鬼成像的首次证明到现在的十年时间里，随着空间调制方法和技术的不断发展，已经发展出了如上文所述的诸多应用。但是由于需要不断变换掩膜(按照Nyquist采样定理的要求，掩膜数量至少与像素数量相同)，与焦阵面成像方案相比，计算鬼成像的采样时间较长。在保证图像信噪比的前提下，如何提高采样速度，以达到准实时乃至实时的成像帧率(>26 frame/s)是目前太赫兹波计算鬼成像需要发展解决的问题。文献[35]的工作实现了1 frame/s的帧率，但是它的像素阵列仅为8×8大小(每个掩膜测量时间22.4 ms)，难以满足实际成像应用场景。而目前的超分辨鬼成像工作[37-38, 41, 44-45]都是基于太赫兹时域光谱系统，受限于系统信噪比，每个掩膜的测量时间都是在秒量级，要得到一幅64×64的图像约需要花费几十分钟甚至数小时的时间。

目前提高帧率的思路主要有两种。一是结合更优化的算法，诸如压缩感知或者自适应成像等，在采样率仅为Nyquist极限的一半甚至四分之一的情况下，仍能获得高保真度的图像。二是提高系统的信噪比，目前的超分辨工作中，都是利用空间编码的激光实现太赫兹波的掩膜测量，而商用的空间光调制器(DMD)最快帧率能达到20 kHz(对应单掩膜测量时间=50 μs)，如果能让单个掩膜测量时间在很短的情况下(小于1 ms)仍能有相当的太赫兹信噪比(SNRµ1/2)，就有望实现准实时的太赫兹波计算鬼成像。

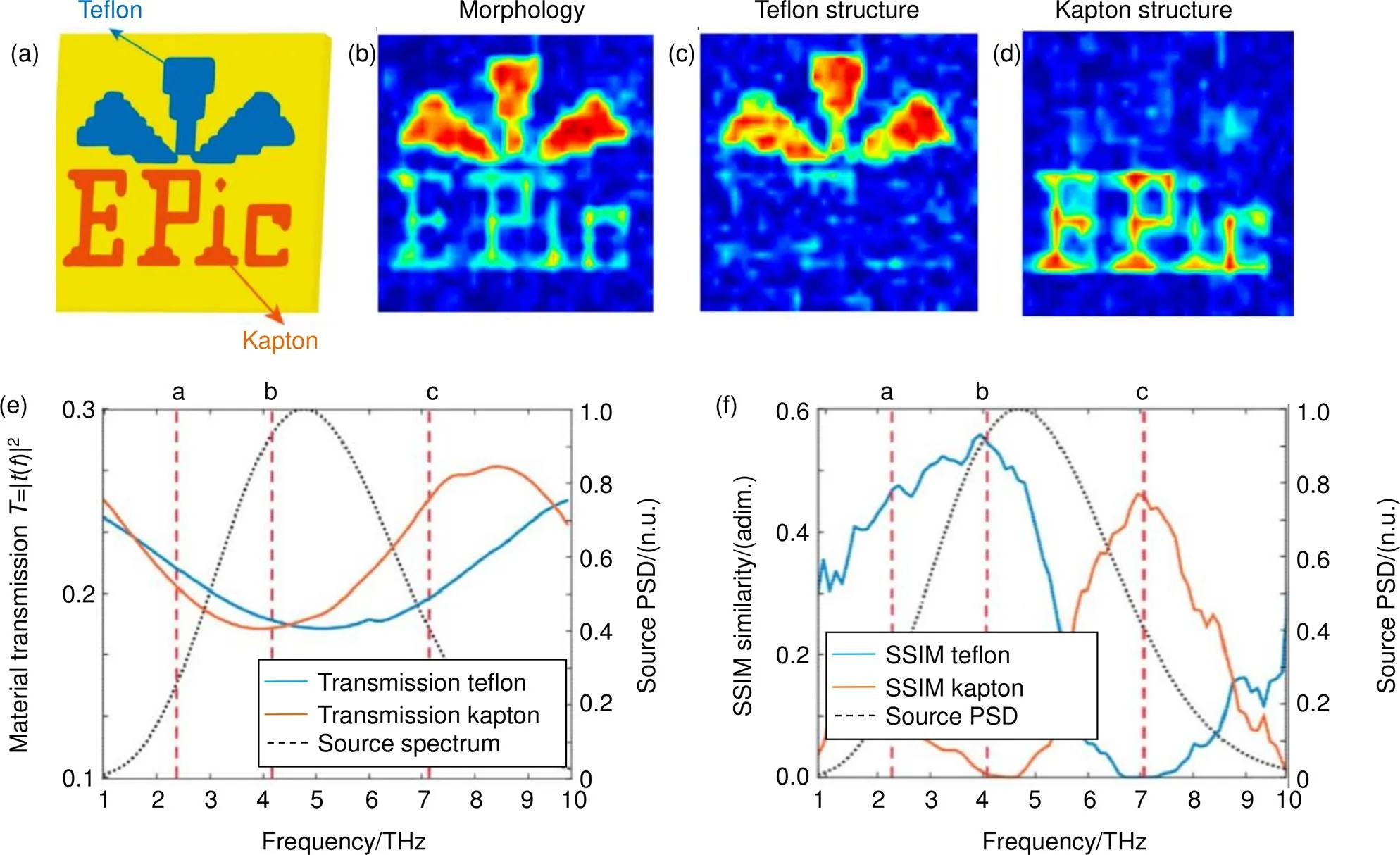
图9 由TNGI技术获得的目标太赫兹光谱图像[46]。(a) 成像目标的示意图，其中黄色部分表示金，蓝色部分表示teflon，红色部分表示kapton；(b)~(d) 目标在不同频点的太赫兹图像；(e) 厚度为10 μm的teflon(蓝色)和kapton(红色)的太赫兹透射幅度谱，其中黑色点线表示入射太赫兹幅度频谱；(f) 不同频点处光谱图像的SSIM (structural similarity index method)。(b)~(d) 所对应的频点在(e)和(f)中用对应的红色垂直虚线标出

[1] Erkmen B I, Shapiro J H. Ghost imaging: from quantum to classical to computational[J].,2010, 2(4): 405–450.

[2] Brown R H, Twiss R Q. Correlation between photons in two coherent beams of light[J].,1956, 177(4497): 27–29.

[3] Brown R H, Twiss R Q. A test of a new type of stellar interferometer on sirius[J].,1956, 178(4541): 1046–1048.

[4] Pittman T B, Shih Y H, Strekalov D V,. Optical imaging by means of two-photon quantum entanglement[J].,1995, 52(5): R3429–R3432.

[5] Abouraddy A F, Saleh B E A, Sergienko A V,. Role of entanglement in two-photon imaging[J].,2001, 87(12): 123602.

[6] Bennink R S, Bentley S J, Boyd R W. "Two-Photon" coincidence imaging with a classical source[J].,2002, 89(11): 113601.

[7] Shapiro J H. Computational ghost imaging[J].,2008, 78(6): 061802.

[8] Duarte M F, Davenport M A, Takhar D,.Single-pixel imaging via compressive sampling[J].,2008, 25(2): 83–91.

[9] Candes E J, Romberg J, Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J].,2006, 52(2): 489–509.

[10] Candes E J, Tao T. Near-optimal signal recovery from random projections: universal encoding strategies?[J].,2006, 52(12): 5406–5425.

[11] Donoho D L. Compressed sensing[J].,2006, 52(4): 1289–1306.

[12] Katz O, Bromberg Y, Silberberg Y. Compressive ghost imaging[J].,2009, 95(13): 131110.

[13] Bennink R S, Bentley S J, Boyd R W,. Quantum and classical coincidence imaging[J].,2004, 92(3): 033601.

[14] Zhang P L, Gong W L, Shen X,. Improving resolution by the second-order correlation of light fields[J].,2009, 34(8): 1222–1224.

[15] Harwit M, Sloane N J A.[M]. New York: Academic Press, 1979.

[16] Tonouchi M. Cutting-edge terahertz technology[J].,2007, 1(2): 97–105.

[17] Meng K, Chen T N, Chen T,.Terahertz pulsed spectroscopy of paraffin-embedded brain glioma[J].,2014, 19(7): 077001.

[18] Zou Y, Li J, Cui Y Y,.Terahertz spectroscopic diagnosis of myelin deficit brain in mice and rhesus monkey with chemometric techniques[J].,2017, 7(1): 5176.

[19] Zou Y, Liu Q, Yang X,.Label-free monitoring of cell death induced by oxidative stress in living human cells using terahertz ATR spectroscopy[J].,2018, 9(1): 14–24.

[20] Hu B B, Nuss M C. Imaging with terahertz waves[J].,1995, 20(16): 1716–1718.

[21] Tang P R, Li J, Du L H,.Ultrasensitive specific terahertz sensor based on tunable plasmon induced transparency of a graphene micro-ribbon array structure[J].,2018, 26(23): 30655–30666.

[22] Van Exter M, Fattinger C, Grischkowsky D. Terahertz time-domain spectroscopy of water vapor[J].,1989, 14(20): 1128–1130.

[23] Nakajima S, Hoshina H, Yamashita M,. Terahertz imaging diagnostics of cancer tissues with a chemometrics technique[J].,2007, 90(4): 041102.

[24] Koenig S, Lopez-Diaz D, Antes J,.Wireless sub-THz communication system with high data rate[J].,2013, 7(12): 977–981.

[25] Nagatsuma T, Ducournau G, Renaud C C. Advances in terahertz communications accelerated by photonics[J].,2016, 10(6): 371–379.

[26] Tang H, Zhu L G, Zhao L,.Carrier dynamics in Si nanowires fabricated by metal-assisted chemical etching[J].,2012, 6(9): 7814–7819.

[27] Xiao Y, Zhai Z H, Shi Q W,.Ultrafast terahertz modulation characteristic of tungsten doped vanadium dioxide nanogranular film revealed by time-resolved terahertz spectroscopy[J].,2015, 107(3): 031906.

[28] Zhai Z H, Zhu H F, Shi Q,.Enhanced photoresponses of an optically driven VO2-based terahertz wave modulator near percolation threshold[J].,2018, 113(23): 231104.

[29] Zhai Z H, Chen S C, Du L H,.Giant impact of self-photothermal on light-induced ultrafast insulator-to-metal transition in VO2nanofilms at terahertz frequency[J].,2018, 26(21): 28051–28066.

[30] Karpowicz N, Zhong H, Zhang C L,.Compact continuous-wave subterahertz system for inspection applications[J].,2005, 86(5): 054105.

[31] Charron D M, Ajito K, Kim J Y,. Chemical mapping of pharmaceutical cocrystals using terahertz spectroscopic imaging[J].,2013, 85(4): 1980–1984.

[32] Yang X, Zhao X, Yang K,.Biomedical applications of terahertz spectroscopy and imaging[J].,2016, 34(10): 810–824.

[33] Chan W L, Charan K, Takhar D,.A single-pixel terahertz imaging system based on compressed sensing[J].,2008, 93(12): 121105.

[34] Shrekenhamer D, Watts C M, Padilla W J. Terahertz single pixel imaging with an optically controlled dynamic spatial light modulator[J].,2013, 21(10): 12507–12518.

[35] Watts C M, Shrekenhamer D, Montoya J,.Terahertz compressive imaging with metamaterial spatial light modulators[J].,2014, 8(8): 605–609.

[36] Landy N I, Sajuyigbe S, Mock J J,. Perfect metamaterial absorber[J].,2008, 100(20): 207402.

[37] Stantchev R I, Sun B Q, Hornett S M,.Noninvasive, near-field terahertz imaging of hidden objects using a single-pixel detector[J].,2016, 2(6): e1600190.

[38] Stantchev R I, Phillips D B, Hobson P,.Compressed sensing with near-field THz radiation[J].,2017, 4(8): 989–992.

[39] Aβmann M, Bayer M. Compressive adaptive computational ghost imaging[J].,2013, 3: 1545.

[40] Green M A. Self-consistent optical parameters of intrinsic silicon at 300 K including temperature coefficients[J].,2008, 92(11): 1305–1310.

[41] Chen S C, Du L H, Meng K,.Terahertz wave near-field compressive imaging with a spatial resolution of over λ/100[J].,2019, 44(1): 21–24.

[42] Liu K, Lee S, Yang S,. Recent progresses on physics and applications of vanadium dioxide[J].,2018, 21(8): 875–896.

[43] Cavalleri A, Tóth C, Siders C W,.Femtosecond structural dynamics in VO2during an ultrafast solid-solid phase transition[J].,2001, 87(23): 237401.

[44] Zhao J P, E Y W, Williams K,. Spatial sampling of terahertz fields with sub-wavelength accuracy via probe-beam encoding[J].,2019, 8(1): 55.

[45] Hornett S M, Stantchev R I, Vardaki M Z,. Subwavelength terahertz imaging of graphene photoconductivity[J].,2016, 16(11): 7019–7024.

[46] Olivieri L, Totero Gongora J S, Pasquazi A,. Time-resolved nonlinear ghost imaging[J].,2018, 5(8): 3379–3388.

[47] Olivieri L, Gongora J S T, Peters L,.Hyperspectral terahertz microscopy via nonlinear ghost imaging[J].,2020, 7(2): 186–191.

THz wave computational ghost imaging:principles and outlooks

Chen Sichao1,2, Du Lianghui1,3, Zhu Liguo1,3*

1Institute of Fluid Physics, China Academy of Engineering Physics, Mianyang, Sichuan 621900, China;2Department of Optics and Optical Engineering, University of Science and Technology of China, Hefei, Anhui 230026, China;3Microsystem & Terahertz Research Center, China Academy of Engineering Physics, Chengdu, Sichuan 610200, China

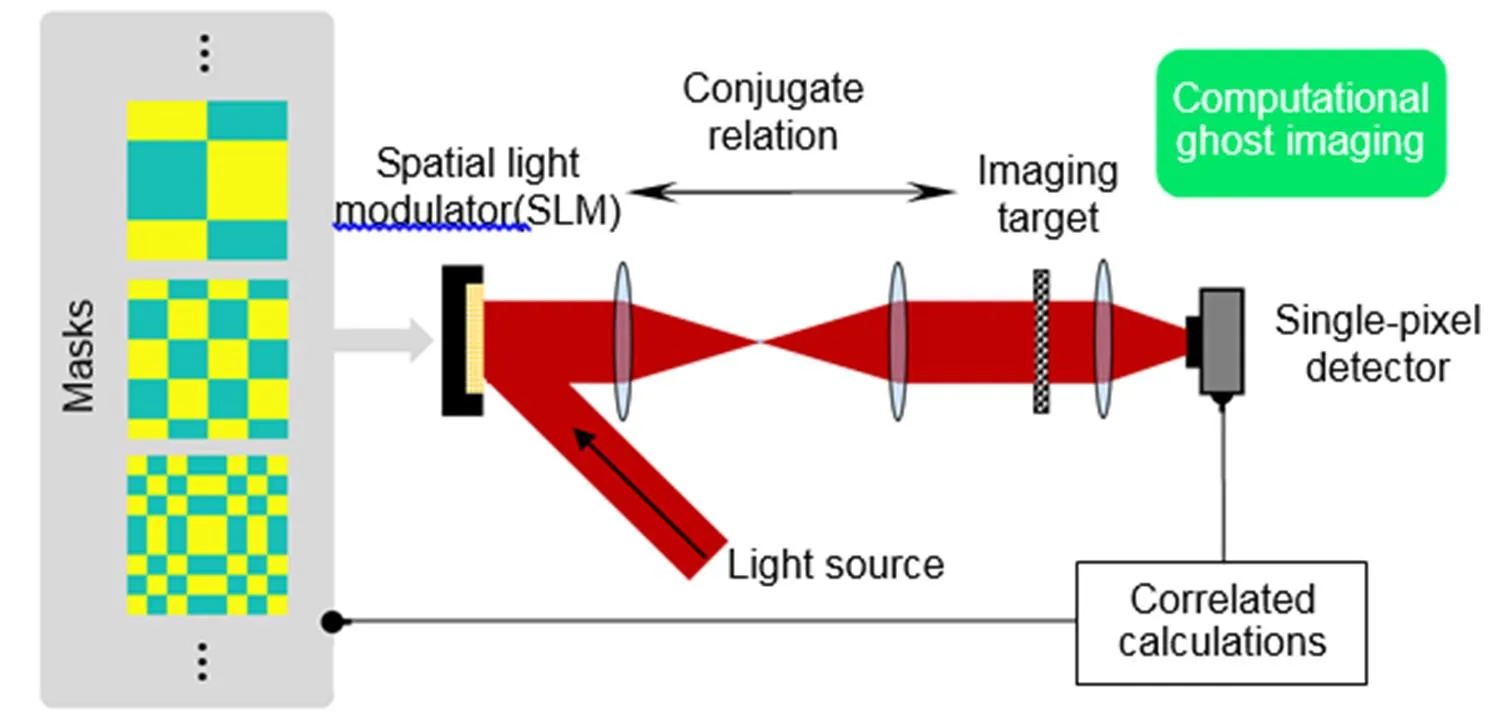
Computational ghost imaging

Overview:Distinguishing from the widely used focal-plane-array imaging (e.g., the charge coupled device, CCD), another novel imaging scheme, computational ghost imaging (which is also called single-pixel imaging or correlated imaging) acquires object’s image by computing the correlations between the varied illuminating field and the imaging target with a no-spatial-resolution detector (single-pixel detector). Comparing with the well-developed silicon-based focal-plane-array cameras, computational ghost imaging is simpler, smaller, and, most significantly, can operate efficiently across a much broader spectral range. Moreover, this imaging methodology can be combined with some novel acquisition technologies, such as compressed sensing and adaptive imaging, making it suitable for many specific imaging applications. On the other hand, terahertz (THz) waves, covering the frequencies ranging from 0.1 THz to 10 THz, have many unique properties, such as the spectral fingerprint, high transmittance in most polar materials, high absorption by water, non-ionizing photon energy (1 THz, 4 meV). There are a lot of applications within THz waves, covering the fields of medical and biology sciences, non-destructive detection, security check, high-speed wireless communication and so on. Imaging with THz waves is also significant in many situations. However, since the focal-plane-array detector available within THz waves is expensive or complicated to fabricate, the main method for THz wave imaging was usually based on raster scanning. The computational ghost imaging within THz waves was firstly demonstrated in 2008, which paves a new route for THz wave imaging and inspires many applications including sub-diffraction-limit THz wave imaging and spatially resolved photoconductivity of graphene. In this article, we firstly review the historical developing process of ghost imaging, namely from the quantum ghost imaging to classical ghost imaging and then to computational ghost imaging. Secondly, the computational ghost imaging is described mathematically in details, including the linear mapping during the imaging process, algorithm for recovering the ghost image and a discussion about the performance of various measurement matrices in noisy imaging environment. And then, we introduce several computational ghost imaging applications within THz waves, including the first demonstration of THz wave computational ghost imaging, the invention of the dynamic spatial THz wave modulator, the sub-diffraction-limit THz wave computational ghost imaging and the photoconductivity mapping of graphene in THz region. At last, we outlook the prospects of the THz wave computational ghost imaging. We hope this review article can help the readers better understand the principles, applications, and prospects of the THz wave computational ghost imaging.

Citation: Chen S C, Du L H, Zhu L G. THz wave computational ghost imaging: principles and outlooks[J]., 2020,47(5): 200024

THz wave computational ghost imaging: principles and outlooks

Chen Sichao1,2, Du Lianghui1,3, Zhu Liguo1,3*

Based on a research hotspot in field of terahertz (THz) wave imaging—THz wave ghost imaging, we first reviewed the development history of ghost imaging: from quantum to classical and then to computational. Second, the mathematical principles of the computational ghost imaging were described in details. Then, we reviewed the development history of computational ghost imaging within THz regime, and its applications including sub-diffraction imaging, photoconductivity mapping of graphene, and hyperspectral THz imaging. At last, we looked towards the prospects of THz wave ghost imaging: as an imaging scheme, ghost imaging avoids the problem that economic and efficient focal-plane-array detectors within THz regime are lacking, whose present frame rates, however, are too slow to meet the requirement for fast imaging. With the improvement of devices’ performance and the optimization of imaging algorithms, we believe that the frame rate of THz wave computational ghost imaging can be significantly enhanced in the future.

ghost imaging; single-pixel imaging; correlated imaging; terahertz waves

National Key Basic Research Program of China (2015CB755405), National Natural Science Foundation of China (U1730246, 11704358, 61427814), and Foundation of President of China Academy of Engineering Physics (201501033)

* E-mail: zhuliguo@tsinghua.org.cn

TN29；O433.1

陈思潮，杜良辉，朱礼国. 太赫兹波计算鬼成像：原理和展望[J]. 光电工程，2020，47(5): 200024

10.12086/oee.2020.200024

: Chen S C, Du L H, Zhu L GTHz wave computational ghost imaging: principles and outlooks[J]., 2020, 47(5): 200024

2020-01-13；

2020-04-13

国家重点基础研究发展规划项目(2015CB755405)；国家自然科学基金资助项目(U1730246, 11704358, 61427814)；中国工程物理研究院院长基金资助项目(201501033)

陈思潮(1992-)，男，博士研究生，主要从事太赫兹计算鬼成像及太赫兹时域光谱技术的研究。 E-mail：amjack@mail.ustc.edu.cn

朱礼国(1983-)，男，博士，研究员，主要从事光学、光电子学、太赫兹科学等的研究。E-mail：zhuliguo@tsinghua.org.cn