基于质心特征和重要敏感区域分类的分形图像压缩算法*
2020-06-02刘增力
王 丽,刘增力
(昆明理工大学信息工程与自动化学院,云南 昆明 650000)
1 引言
随着数字技术的发展,越来越多的信息通过图像形式传递,对大量图像数据信息进行高效的存储和传输是当今信息时代所面临的重要问题,除硬件本身需要改善外,高性能的图像压缩技术变得越来越重要。以分形为研究对象的分形几何是现代数学的一个新分支,其本质是一种新的世界观和方法论。
常用的图像压缩技术可以分为有损压缩和无损压缩2类,无损压缩包括Huffman编码、行程编码、LZW编码和算数编码等,有损编码包括预测编码、JPEG编码、变换编码和矢量编码等。2种类型的编码满足不同需求,无损压缩完全保留图像质量,而有损压缩以牺牲一定的图像质量,在确保恢复效果的前提下,大幅度提高了图像传输速度和存储量,面对大量的数据交互,具有广阔的应用前景。分形编码是一种有损图像压缩技术,它是图像压缩的一个重要工具。分形图像压缩利用了自然景物的自相似性来进行数据压缩,以迭代函数系统为理论基础。Barnsley等[1]最早给出了分形编码的大致过程,即利用提取的分形子图,寻找整体与局部之间存在的某种自放射特征。在实用化研究中,Jacquin[2]提出了分形块编码,通过对图像的分割分别获得互不重叠的小方块和重叠的大方块,然后对每个小方块搜索与之最仿射相似的大方块。Jacquin型编码把分形编码从“专家算法”变成“大众算法”,分形编码才真正被运用到众多领域中。
2 相关研究
近年来,国内外涌现出越来越多基于Jacquin型编码的分形图像编码技术。研究者主要从图像分割方式、结合变换域、码本缩减、匹配方式和解码方式等方向展开研究,研究的目的都是减少分形编码时间过长对编码效率带来的影响,以及确保重构图像质量。基于变换域的分形图像编码方法在分形编码之前对图像进行处理,对处理后的图像采用分形编码,文献[3 - 5]提出的分形与小波变换结合的混合编码方法、谢敏等[6]提出的分形与DCT结合的混合编码方法,都取得了良好的图像恢复效果。Gupta等[7]提出的空域和频域结合的方法,将块分类转换为空域分类,简化了分类方式。结合其它编码方式的混合分形编码方法也被研究者尝试,其中王春梅等[8]将算数编码结合分形编码的方法很大程度上提高了编码效率。朱志良等[9]提出的基于像素的三角分割方式,可以对图像不同纹理分布采取不同大小的块分割,有效保留了图像的重要信息。基于码本缩减的分形编码方法有很多,其中李高平等[10]提出的方差剔除条件的快速分形图像编码方法、何传江等[11]提出的基于平均偏差排序的快速分形图像编码方法、Roy等[12]提出的基于缩放参数上限的方法,将原始码本中不符合条件的码本剔除,减少了匹配次数,编码时间大大缩短。Ismail等[13]提出的结合布谷鸟搜索优化算法的分形编码算法,改变以往传统欧氏距离搜索方式,取得了不错的效果。孔玲君等[14]根据人眼对图像的视觉选择特点,提出了感兴趣区域压缩方式,使得人眼对恢复图像视觉效果增强,也间接地缩减了码本。为了达到缩短编码时间的目的,最直接的方式就是以图像恢复质量换取编码时间。相比直接剔除码本,块分类是一种折衷的方法,如汪玮玮等[15]提出的分类父块方法、何传江等[16,17]提出的叉迹特征分类方式以及张璟等[18]提出的双交叉和特征分类方法,都实现了块分类过程,达到了缩减编码时间的目的。
本文提出一种基于质心特征和重要敏感区域划分的分类算法,质心被广泛应用于目标跟踪和目标识别中,可以作为特征使用,本文将质心应用到灰度块图像匹配中,提取子块不同的质心坐标,达到分类块的目的。同时,考虑人眼对图像的整体轮廓和部分细节较为敏感,以及对重要区域选择关注的特点,对人眼视觉专注部分着重处理,增加图像恢复好感度。
3 本文算法
3.1 基本算法
在基本分形编码算法中,原始图像首先被分割成互不重叠且大小为n×n的Range块(简称R块)和允许重叠且大小为2n×2n的Domain块(简称D块)。然后,将每个D块通过4-邻域像素平均算子压缩为n×n的子块,与R块大小匹配,而所有压缩后的D块经过8种等距变换后就构成码本Ω。
在编码阶段,对每一个R块,按照全搜索方式在码本Ω中寻找其最佳匹配D块和自仿射变换ω,使得ω(D)与R的均方误差均达到最小。为了寻找R块的最佳匹配块,需要求解下述极小化问题[19]:
‖R-(s·Dm+o·I)‖=
(1)
其中,m表示R块的最佳匹配块序号,s表示对比度收缩因子,o表示亮度偏移,I∈Rn×n是所有元素均为1的常值块。
直接求解式(1)十分困难,耗时很长,为了降低复杂度,先忽略内层约束|s|<1,将极小化问题(1)转化为下述问题求解:
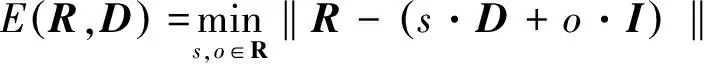
(2)
问题解为:
(3)
(4)
3.2 质心特征
分形编码的绝大多数时间都是花费在R块与码本中D块进行全局搜索匹配的过程中,特征算法的目的就是避开全局搜索,将搜索过程转换成为局部搜索,每次搜索限定在一定特征下的有限区域内。
质心在几何图形中可以表示质量中心,即重心,对于规则的均匀物体,质心在其几何中心,图像同样存在质心。下面证明在分形图像压缩编码中,利用质心特征进行分类的可行性。假设子块G,G(i,j)表示G中(i,j)处的值,其质心定义如下:
(5)
定义1子块G=(G(i,j))∈Rn×n的归一化定义为:
(6)
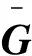
取归一化后的值为特征值,定义子块x和y方向的质心特征如下所示:
(7)

定理1对于R块和D块,设R,D∈Rn×n(n为偶自然数),则有如式(8)所示的关于R块和D块匹配误差的不等式成立:
(8)
其中,C′trx(R),C′try(R),C′trx(D),C′try(D)分别是定义的新质心特征。
证明过程见附录。
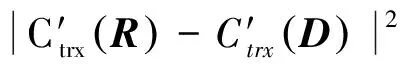
3.3 质心特征选取
用一个子块的质心特征代表整幅图像过于宽泛,因此本文采用求取R块的多个质心的方法,联合进行特征划分。假设图像块X=(xi,j)∈Rn×n,n=8,如图1a所示,将图像块X分为如图1b所示的4个部分,Xk∈Rm×m,k=1,…,4,m=4,对每一个Xk求质心。大量的实验表明,图像质心分布于4个可能的位置,如图1c中a、b、c、d所示。对于图像块X而言,质心的分布情况有44=256种。为了减少质心分类数,本文采用如图1d所示的处在对角线位置的2个部分的质心作为分类标准,将质心分布情况减少到42=16种,从实验中发现,图像块质心的分布具有相似性,往往分类不会达到16种。

Figure 1 Centroid position图1 质心位置
4 重要敏感区域划分
4.1 敏感区域划分
在分形图像压缩中,需要对图像进行分割处理,与整幅图像相比,子块的结构比较单一,且往往在很多结构上具有相似性。通常根据R块的结构分布可以将R块划分为不同的归属类,其中一个评判标准是方差。对于子块而言,方差小表示该子块像素值变化波动趋于平缓,即结构平滑;方差大表示该子块像素值变化相对很大,即属于纹理或边缘等细节区域。
研究表明,人眼视觉系统对边缘比对平滑区域更敏感,也就是说,人眼的注意力会更集中在提供信息的区域,对于图像的边缘、纹理、平滑区域,人眼敏感程度逐渐递减。为此,根据人眼对图像区域的敏感程度,将图像划分为敏感区域和非敏感区域。R块在码本中的最佳匹配块一定与该块最接近,包括灰度级的接近和灰度变化的接近,非敏感区域采用均值替代参数的方式,以此来缩短编码时间。假设R块的非敏感区域划分阈值τ是固定的,R块划分方法如下所示:
σ<τ
(9)
其中,σ为R块方差,若满足式(9)即可认为R满足非敏感区域条件,便用均值取代搜索匹配参数,否则认为R块为敏感区域。
4.2 重要区域
人眼视觉能感觉到的重要区域一般为图像的中心1/4部分,因此对这部分着重处理会增加人眼对图像的好感度。这部分图像往往会被第一眼看到,基于此,本文将原始图像分为2部分,分别为中心1/4面积部分的重要区域和其余的非重要区域。对重要区域的编码采用更加精细的匹配编码,对该区域内的非敏感区域划分使用的阈值τ′不同于式(9)中的阈值τ,二者满足τ′<τ,这样可以使得更多处在重要区域内的R块进行全局匹配,进而使重要区域图像灰度质量提高。重要区域划分如图2所示。

Figure 2 Sensitive area图2 重要区域
5 算法分析与实现
对于输入的R块和D块,由式(8)知,如果R块和D块的质心特征相差较大,则二者的均方误差Ex(R,D)和Ey(R,D)也相差大,即整体均方误差E(R,D)也会大,从而导致D块不能与R块匹配。对应地,如果D块是R块的匹配块,那么二者的整体均方误差就会较小。因此可以认为,如果R块和D块互为匹配块,那么二者也是在质心特征下的近邻。需要指出,R块和D块在质心特征下相差小,不一定代表E(R,D)也小,从而R块和D块在特征意义下的最佳匹配并不能保证D块是R块在最小均方误差下的最佳匹配块。尽管特征意义下R块和D块匹配不能保证均方误差下二者的匹配,但是最佳匹配D块距离也不会太远。本文采用扩大搜索半径的方法,在特征意义下以最佳匹配D块为中心,距离L为半径,步长K进行搜索,寻找更大范围内的最佳匹配块。
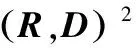
(10)
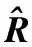
基于以上推导,本文算法的具体步骤如下所示:
步骤1将原始图像分割成为不重叠的大小为n×n的R块,以横纵方向步长为Δ生成可重叠且大小为2n×2n的D块,采用邻域平均方法将D块大小变为n×n,并构成码本Ω。
步骤2将原始图像划分出重要区域和非重要区域,设置阈值τ′、τ、η、搜索半径L以及步长K。
步骤3对重要区域使用阈值τ′进行敏感区域划分。若R块满足σ<τ′,则认为其是敏感区域,求取并存储其平均值aver作为参数;若R块满足σ>τ′,则认为其是非敏感区域。对敏感区域R块在码本Ω中进行质心特征匹配,寻找匹配块Dm,以Dm为中心,L为搜索半径,K为步长搜索最佳匹配块D′m,并存储参数。当满足E(R,D′m)<η,搜索结束。
步骤4对非重要区域使用阈值τ进行敏感区域划分。满足σ<τ认为是敏感区域,求取并存储平均值aver作为参数;满足σ>τ认为是非敏感区域。对敏感区域R块在码本Ω中进行质心特征匹配,寻找匹配块Dm,以Dm为中心,L为搜索半径,K为步长搜索最佳匹配块D′m,并存储参数。当满足E(R,D′m)<η,搜索结束。
步骤5对于所有R块,重复步骤2~步骤4,其中将处在重要区域与非重要区域边界的R块判定为重要区域。
6 实验结果与仿真
实验中采用的图像是Matlab标准库中图像,大小分别有256×256和512×512,R块大小取用4×4,D块大小取用8×8,D块划分间隔为8像素,半径L为40像素,步长K为4像素,图像恢复效果采用人眼观察、峰值信噪比PSNR(Peak Signal to Noise Ratio)、重要区域峰值信噪比SAPSNR(Sensitive Area Peak Signal to Noise Ratio)、编码时间、解码时间和压缩比进行评价。其中SAPSNR值作为重要区域的峰值信噪比[5],即等于恢复图像中心1/4部分的PSNR。
本文参考2种特征类似的算法,分别是张璟等人在文献[18]提出的双交叉和特征算法、何传江等人在文献[16,17]中提出的叉迹特征算法,以及基本分形图像压缩方法,对重要区域峰值信噪比(SAPSNR)进行对比;同时为了观察图像敏感区域恢复效果,计算恢复图像子块均方根大于4的部分的峰值信噪比。李高平等人在文献[10]中认为均方根小于4的部分的子块为敏感块,对比实验中采用统一阈值τ=4。本文算法非重要区域采用敏感区域阈值τ=4,对于重要区域阈值τ′=3。
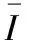
(11)
(12)
(13)
SAPSNR=
(14)
恢复图像的压缩比CR(Compression Ratio)的计算方式如式(15)所示:
(15)
其中,Num1表示图像经过压缩后传输过程中数据量,Num2表示图像不经过压缩直接传输所需要数据量。
表1所示为基本分形算法、双交叉和特征算法以及本文质心特征算法的实验结果,其中C代表Cameraman图像,L代表Lena图像,P代表Peppers图像,PSNR(Sensitive area)代表恢复图像中满足敏感区域条件的PSNR值的和。从表1可看出,本文算法相比文献中算法压缩效果更好。
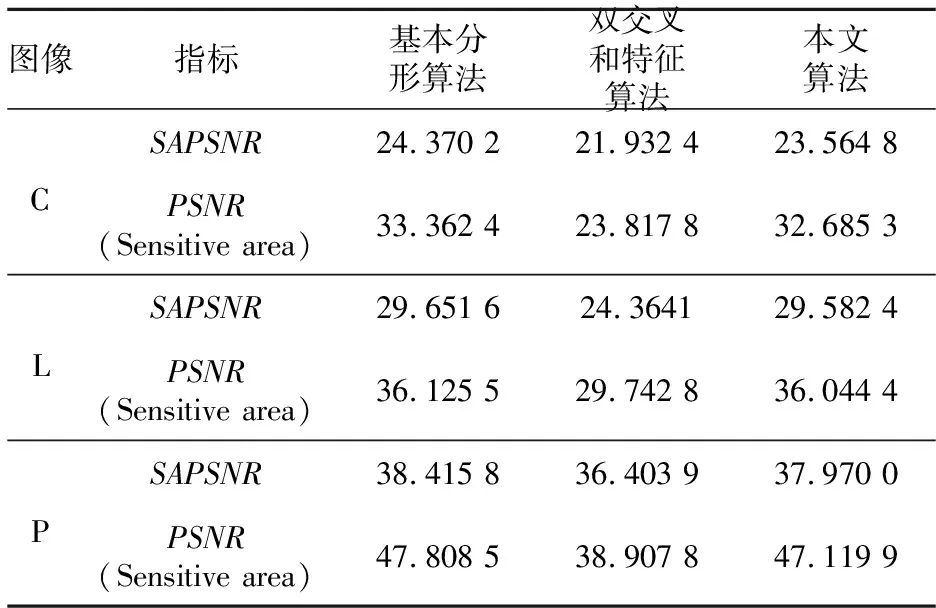
Table 1 PSNR(Sensitive area) and SAPSNR value comparison
如表2所示,实验中选用的搜索半径L与R块长度相同,步长K为R块长度的10倍,本文算法在PSNR值可以接受情况下,编码时间相较于基本分形图像压缩算法,最高可节省大约64%。
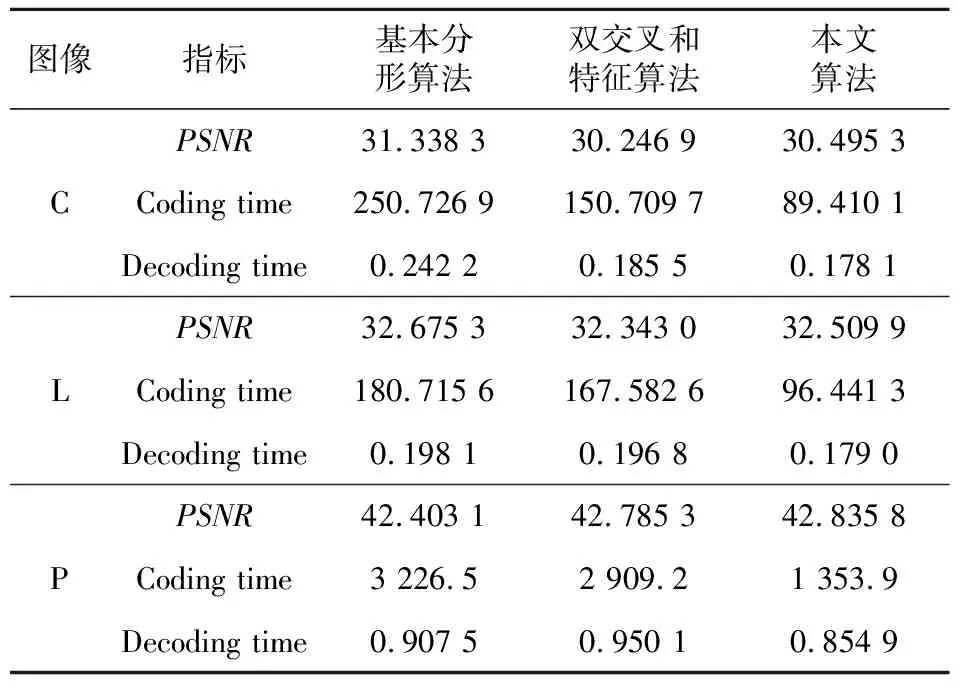
Table 2 Image PSNR,encoding time,decoding time simulation results of C image
分形图像压缩算法未划分敏感区域和重要区域,采用全局搜索方法,从表3中可以看出,CR值与块大小成反比。双交叉和算法非敏感区域阈值τ都取4。本文算法中,重要区域内敏感区域划分阈值取3,非重要区域内敏感区域阈值取4。
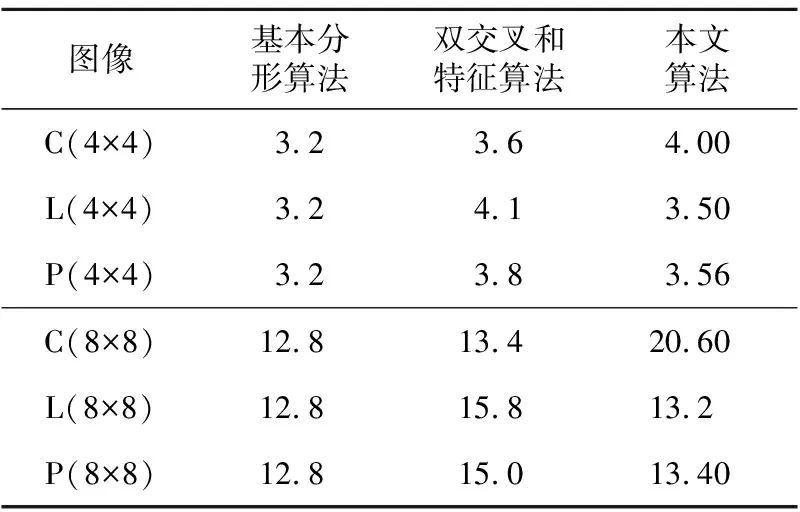
Table 3 Compression ratio of algorithms under different block sizes
图3是实验图像在不同算法以及不同块大小下的恢复图像,图像大小分别为256×256,256×256,512×512,512×512,从左至右分别为原始图像、基本算法恢复图像(4×4)、本文算法恢复图像(4×4)、交叉和算法恢复图像(4×4)、基本算法恢复图像(8×8)、本文算法恢复图像(8×8)。从图3中可以看出,本文算法恢复的图像效果比双交叉和算法恢复的效果更好。
7 结束语
本文提出了一种质心特征和重要敏感区域分类的分形图像压缩算法,利用图像块质心特征,对相似图像块进行近似匹配,在分形图像压缩编码阶段,利用质心特征对R块和D块进行匹配,有效缩短了编码阶段的时间。同时考虑人眼对图像敏感区域和重要区域的选择,采用重要区域和敏感区域划分方法,增加人眼对恢复图像效果的好感度。实验结果表明,质心特征分类和重要敏感区域划分处理的分形图像压缩算法相比传统算法可以在编码时间和恢复图像效果上取得优良效果,同时分类过程中的参数可调整,例如敏感区域划分阈值、搜索步长和半径等,具有较强的灵活性和直观性,具有较好的应用前景。

Figure 3 Recovery results图3 恢复结果
