带电跨越施工被牵导线与封网碰撞仿真分析

孟遂民 申 威 唐 波

(三峡大学 电气与新能源学院， 湖北 宜昌 443002)

近年来，特高压工程建设发展十分迅速，输电线路之间的交叉跨越日益频繁，在交叉跨越施工中如何保证施工安全是问题的重中之重[1].经过多年的实践与发展，无跨越架封网在跨越高压超高压带电线路等施工中应用得越来越广泛[2].无跨越架架线施工技术通常采用局部封网，其典型结构由承载索、绝缘网、绝缘网撑杆等部件组成.封网结构主要用于预防张力牵引和紧线过程中牵引绳或导线断裂后跌落造成的闪络停电事故.由于这种突发故障对不停电跨越架线施工是最危险的工况，因此，研究封网受跌落导线冲击过程中的垂直位移与结构强度变化十分必要.

跌落导线与封网结构发生碰撞的动力过程具有高度非线性，目前主要通过数值模拟技术进行研究.夏拥军，胡院生，万建成，等[3]建立封网有限元模型进行动态冲击仿真，将结果与静力学结果进行对比分析后，指出采用静力学方法不能准确地评估封网的安全性.陈保家，朱晨希，周幼辉，等[4]使用棒料等效断线导线与跨越架封网碰撞，模拟计算了不同工况下承载索受冲击的变化规律.胡院生[5]研究了导线对于封网杆的冲击，指出动态冲击载荷具有持续作用时间较短，冲击过程呈瞬时性的特点.然而，以上研究采用集中载荷或冲击系数的方法模拟导线对封网的冲击，而对导线-封网跌落碰撞模拟尚未见诸报道.然而封网装置受张力导线跌落冲击时，其载荷分布、载荷类型、几何拓扑改变与等效质量块或冲击系数模拟导线截然不同.因此，如何通过已有研究成果对导线-封网碰撞进行模拟，分析封网在导线冲击过程中垂直位移与结构强度的变化成为难点.

本文综合隐式-显式有限元仿真方法[6]，建立一套导线-封网从建模到碰撞的全过程仿真流程，并以某带电跨越架线工程为例，再现导线跌落对封网装置产生碰撞冲击的全过程.实现了对封网装置受跌落导线冲击碰撞过程仿真，并对碰撞过程中封网的垂直位移与结构强度变化进行了分析，可为封网结构弱点分析、安全设计提供重要参考.

1 断线事故及仿真难点

输电线路架设施工导线被牵引过程中，导线经过放线滑车时，放线滑车可能发生偏移，使导线或牵引绳受力过大断裂，被牵导线跌落后对封网产生冲击，给被跨带电线路带来极大安全隐患(如图1所示).因此，研究断线事故对确保跨越架线施工安全具有重要意义.

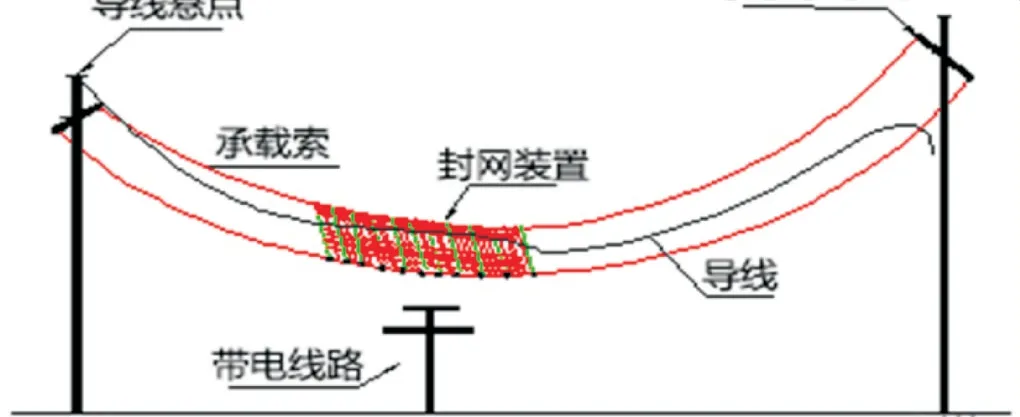
图1 导线与封网结构碰撞事故状态图

然而导线与封网的冲击过程是非常复杂与困难的动力学问题.传统方法通过集中载荷或冲击系数模拟导线对封网的冲击，而不考虑预应力导线对整个结构动力响应的影响显然是不准确的.若充分考虑预应力对结构动态响应的影响，则需要将导线与封网碰撞过程的数值仿真分为两步进行：第一步搭建施加预应力的导线-封网模型；第二步预应力导线冲击封网.传统意义上这两步需分别用到隐式分析与显式分析，会使得这类问题变得无法解决.因此，为了解决这类多工步加载的复杂问题，需要综合隐式与显式求解器，即序列求解.

采用隐式-显式序列求解法，先通过隐式求解器得到导线与封网装置的预应力，然后在显示动力分析之前将其施加于结构之上，最后通过显式求解器对导线冲击封网时的动力响应进行分析.通过隐式-显式序列求解法，解决了单独使用显式或隐式无法解决的多工步加载的问题，使模拟与实际更加符合.

2 碰撞仿真原理与流程

2.1 碰撞仿真原理

导线与封网的碰撞过程中存在大变形、大位移等多维非线性问题.LS-DYNA 方程因其非耦合，且具有不需要进行非线性刚度矩阵逆运算的优点，因此能够有效解决高度非线性问题求解不收敛的问题[7-8].

进行跌落导线冲击作用下封网动力分析时，其动力方程可表示如下：

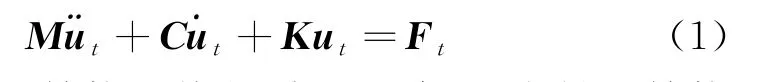
式中：M为封网结构系统的质量矩阵；C为封网结构系统的阻尼矩阵；K为封网结构系统的刚度矩阵；¨ut为加速度矩阵，˙ut为速度矩阵，u为位移矢量矩阵；Ft为导线冲击引起的载荷向量.

将式中的加速度与速度通过位移表示，并使用中心差分替代微分，则可分别表示为：

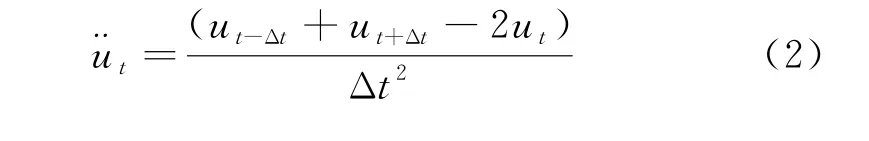
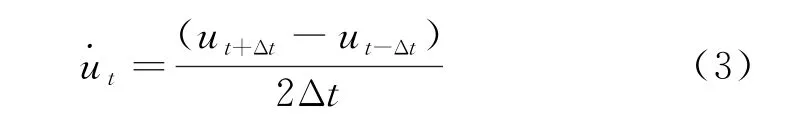
将式(2)、(3)代入式(1)通过整理得：

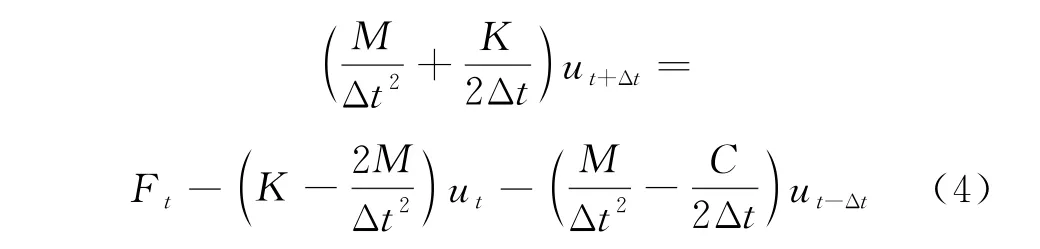
由上述推算可知，使用中心差分法只需将初始条件代入，即可得t+Δt

时刻的瞬时封网结构的各个位移量ut+Δt，再将ut+Δt代入物理与几何方程中便可求得t+Δt时封网结构各个单元的应力与应变[9-10].由此，可以得到封网结构各个时刻的垂直位移量与对应时刻的结构强度参数.

2.2 仿真流程

采用ANSYS/LS-DYNA 软件，运用隐式-显式联合算法的导线与封网结构碰撞仿真流程如图2所示.

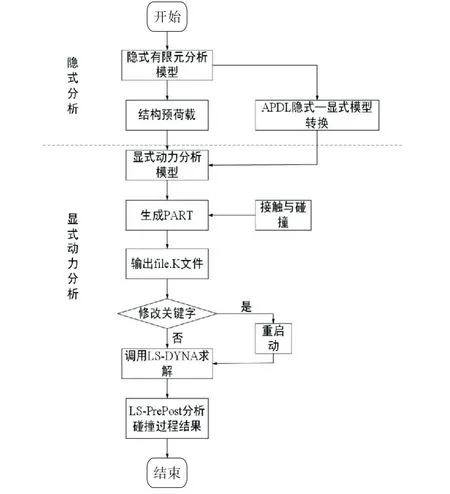
图2 导线与封网结构碰撞仿真流程

由图2可知，由隐式分析实现导线与封网结构预应力的施加，通过APDL 编制程序将隐式与显式模型等效转换后，显式分析应用LS-DYNA 技术，求解导线跌落冲击封网过程的非线性问题，充分考虑了冲击过程中的接触与碰撞，进而实现导线跌落冲击封网的动力学仿真.

3 工程实例及参数设定

3.1 工程概况

某带电跨越张力架线工程，档距369m，高差4.3m；导线悬挂于封网上方，型号为LGJ-500/45，与封网承载索悬挂点高差2.2m；封网部分长70m，宽6m，左侧距左悬挂点的水平距离260m.封网装置下方带电线路电压等级500kV，该线路与新建线路交叉角为90°.架线采用一牵四放线，放线张力为104000N.

3.2 材料参数

选用规格为Ф16mm 迪尼玛绳作为封网结构的承载索，其单根应力为40.52MPa，绝缘网撑杆则选用规格为Ф50mm 圆形环氧树脂绝缘杆，绝缘网选取规格为Ф12mm 的高强度锦纶绳网，具体参数见表1.

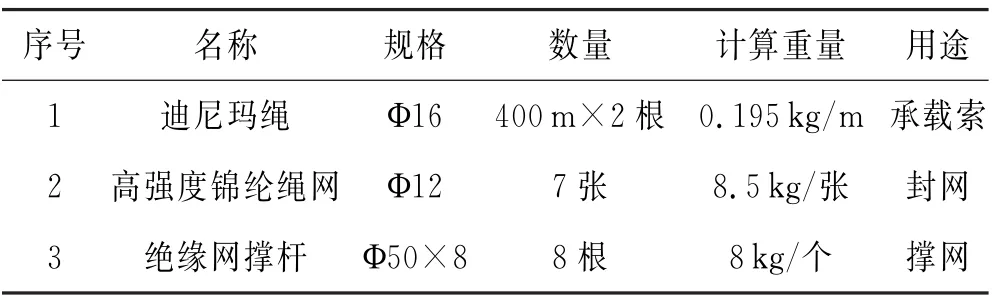
表1 封网跨越结构参数

3.3 仿真关键参数

导线、承载索、绝缘网视为柔性结构，选用LINK10单元.绝缘网撑杆能够承受拉力和弯矩，使用BEAM4梁单元.撑杆与承载索铰接[11-13].假设导线在跌落过程中不受风荷载等环境因素影响，导线跌落于封网中央.导线跌落与封网结构碰撞属于大变形，为防止模拟仿真构件间发生不真实穿透，选用

LS-DYNA 提供的罚函数法作为接触算法，并设置接触类型为自动单面 AG[14-15].

4 仿真结果与分析

为了分析出现断线事故时封网结构的位移与力学特性，采用上述方法，对LS-DYNA

动力有限元模型施加预应力，对导线与封网的碰撞过程进行仿真.根据有关参数搭建导线-封网有限元模型，如图3所示.

图3 导线-封网跨越结构有限元模型

4.1 导线封网碰撞过程分析

导线-封网模型建立后进行碰撞仿真，仿真以牵引绳断线时刻作为起始点，计算时长10s，得到的不同时刻导线与封网碰撞的变形仿真结果如图4所示.

图4 导线与封网变形图

由图4(a)可知，t=0s时，在牵引张力和重力作用下导线出现一定形变位移，牵引绳断线，导线开始下落.当t=1.28s时，导线与封网结构右侧第一个绝缘网撑杆接触(如图4(b)所示)，冲击碰撞开始.图4(c)为导线跌落在封网结构上，封网受到冲击，承载索形变由最开始受到冲击的最右侧绝缘撑杆处向左传播，导致封网各段绳索产生振动，跌落在封网外的导线以最右侧的绝缘杆为节点，作锤摆运动.图4(d)为封网装置上的绝缘网与绝缘撑杆继续振动，绝缘撑杆1与撑杆8(如图4(b)所示)均有较大形变.

4.2 垂直位移分析

承载索与封网结构在承接跌落导线的过程中，需要始终保证与下方被跨带电线路有足够的安全距离.在实际工程中多以封网两端跨越点(封网装置末端和承载索的连接处)到被跨线路的垂直距离为准，因此需要确定封网两端跨越点在垂直(Y)方向的最大位移.为此选取封网结构两端作为跨越点的两个节点965、627，以及绝缘网撑杆1和8中间位置的两个节点1615、1604(如图4(b)所示)进行分析，其Y方向的位移时程曲线如图5所示.

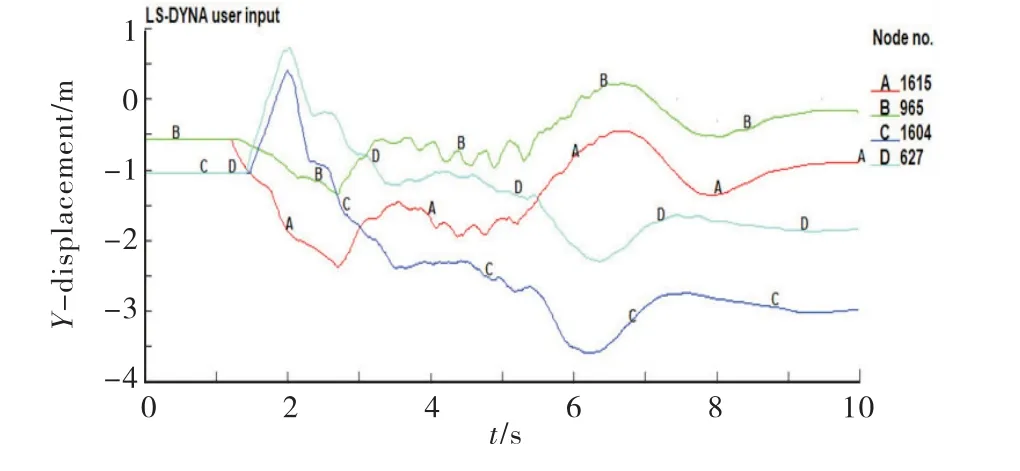
图5 有关节点的位移时程曲线

由图5可知，上述节点垂直方向均具有初始位移，其中1615号与965号节点，1604号与627号节点垂直位移趋势相同，表明绝缘撑杆中间节点与其承载索连接处节点位移基本同步.但两组节点运动趋势不同，靠近断线点一侧节点运动呈一侧先下降后上升，另一侧先上升后下降，且绝缘撑杆中间节点位移大于其承载索连接处节点垂直位移.在t=2.76s时，1615号节点运动至最低点，相对其初始位置向下垂直运动了1.93m.在t=6.21s时，1604号节点达到最低点，相对其初始位置向下垂直运动了2.65m.1604节点最大位移大于最先受到冲击的1615节点.因此，封网装置最先受到冲击点的垂直方向上的最大位移不一定最大，考虑电气距离时，应以整个碰撞过程中封网两端绝缘杆中间位置的最大垂直位移为准.

4.3 结构强度分析

绝缘网撑杆和承载索是封网结构中的主要受力部件，其中绝缘网撑杆用于支撑绝缘网，在封网结构受到导线冲击后仍能保证绝缘网张开足够的保护面积来承接跌落导线.撑杆1最先受到断线冲击，其承受冲击力最大，故选取撑杆1的跨中截面进行分析，截面压弯应力时程曲线如图6所示.

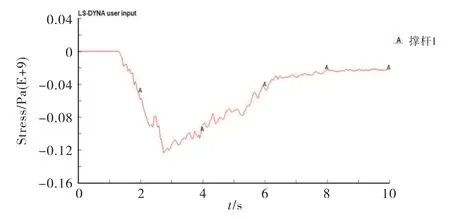
图6 绝缘网撑杆1跨中截面压弯应力

由于碰撞过程中撑杆1受力状态复杂，且存在较多的相互作用，截面压弯应力存在震荡现象.观察图中曲线走势，可以发现碰撞过程中撑杆1跨中截面压弯应力方向没有改变，其承载机制反映出撑杆1一直是受压杆件，承受压弯应力.此外，由图6可知撑杆1跨中截面压弯应力在t=2.81s时达到最大，最大值为-123.1MPa.其最大压弯应力小于撑杆可承受的极限应力，由此可知，封网结构最右端绝缘网撑杆在导线与封网结构碰撞过程中撑杆1不会被破坏.

导线跌落至封网结构上时，承载索同样承受着较大的冲击荷载，因此承载索的安全也至关重要.为了确保承载索在该工况下不被破坏，就需要了解其主要单元所要承受的最大张力.

由于导线跌落于封网中央，所以两承载索的冲击情况相同，为此仅需要对一根承载索进行分析，其选取的承载索单元具体位置如图3所示.由表2可知，靠近断线点一侧承载索单元的最大张力大于另一侧，靠近断线点的封网装置末端与承载索连接处的969号单元最大张力最大，最大值为33193.1N.

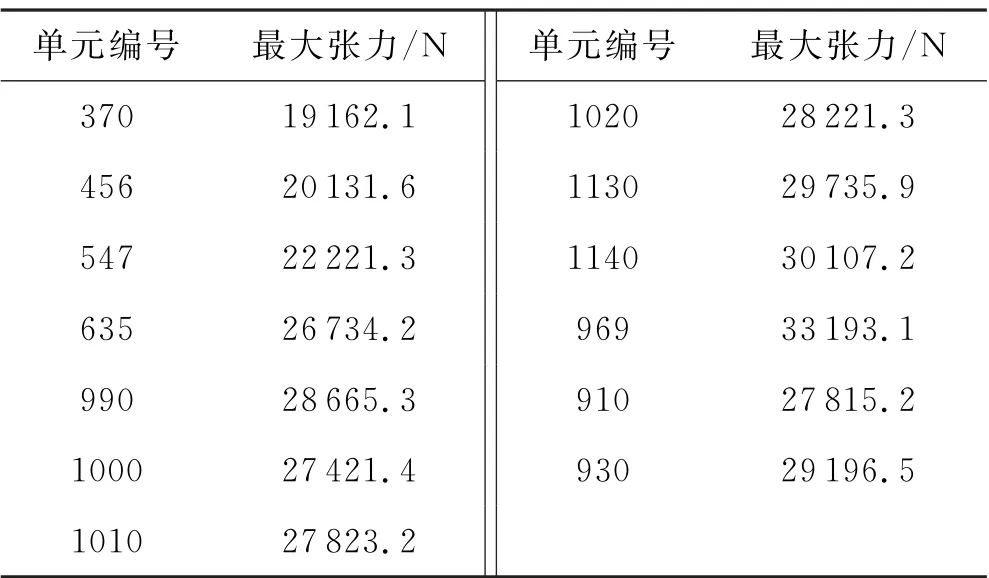
表2 承载索主要单元最大张力

依据本文相关参数，通过等效载荷与架空线状态方程计算，分别得到事故状态下撑杆1截面压弯应力-119.4MPa，承载索张力32329N，其与仿真结果相比误差均小于5%，误差值在允许范围内，证明了仿真计算的可行性与有效性.

5 结 论

1)为了准确分析断线事故状态下封网结构的动态响应，充分考虑导线与封网预应力的影响，建立相应数值仿真技术流程，通过隐式-显式序列求解法，解决了结构预应力施加与碰撞的多步仿真问题.

2)实现了导线与封网碰撞的全过程模拟，分析了碰撞过程中封网结构垂直位移变化与结构强度，通过理论计算验证仿真的可行性，可为后续封网结构材料选择、强度设计提供理论依据.