水轮发电机组多回路鲁棒调速控制研究

李文武 余 跃 徐 康 石 强 吴永华 童华敏

(1.三峡大学 电气与新能源学院， 湖北 宜昌 443002； 2.梯级水电站运行与控制湖北省重点实验室(三峡大学)， 湖北 宜昌 443002； 3.国网湖北省电力公司孝感供电公司， 湖北 孝感 432000； 4.国网湖北省电力公司宜昌供电公司， 湖北 宜昌 443002)

水轮发电机组调速系统是实现水电快速响应负荷变化的重要控制系统.该非线性系统包含液压部分、机械部分和电气部分，其动态特性在很大程度上取决于内部不确定性和外部扰动[1].水轮发电机组调速系统的一般研究均假设其模型参数等均为常数，PID 控制因简单实用而得到广泛应用[2].

实际上水轮发电机组调速系统的很多模型参数并不确定，例如波传播时间、水启动时间、发电机转动惯性时间系数、发电机阻尼系数、伺服电机和伺服系统时间常数等[3].传统控制方法已不能满足水电机组非线性特性以及负荷变化等扰动的需求[4].随着新能源大量接入电网，水轮发电机组承担电网更频繁的负荷变动，其调速系统的设计仍是一个有待深入研究的问题.

PID 控制不适用于水轮发电机组调速这类复杂的非线性系统，并且很难处理模型参数不确定问题[5].文献[6-8]采用预测控制、自适应控制、模糊控制等处理水轮发电机组调速器中的不确定因素.以上几种方法对模型的精度要求比较高且水轮发电机组调速系统对大干扰的响应不够理想.

鲁棒控制是处理不确定系统的常用控制理论，已在航天控制、电动车控制等领域得到成功应用[9].鲁棒控制系统可在不确定情形下仍能保证闭环系统的控制性能[10].文献[11]运用混合灵敏度方法设计水轮发电机组双回路鲁棒调速控制系统.文献[12]在文献[11]应用不足的基础上使用μ综合方法设计PI控制系统.由于混合灵敏度方法没有达到理想的鲁棒性能，文献[13]则在文献[11]的基础上用μ综合方法对外环进行控制，水轮发电机组调速系统具有良好的鲁棒稳定性.

上述采用鲁棒控制理论进行水轮发电机组调速系统设计时，仅针对伺服系统、水轮机和发电机整体建立双回路控制模型，未针对水轮机和发电机单独设置控制回路，导致鲁棒控制效果仍有待提高.因此在文献[13]的基础上，提出水轮发电机组多回路鲁棒调速控制策略，构建分别包含伺服系统、水轮机和发电机的3个互相嵌套的控制回路，并使用鲁棒控制中的混合灵敏度方法和μ综合方法进行设计.

1 水轮发电机组单回路控制模型

1.1 水轮发电机组调速系统结构

水轮发电机组由水力系统、水轮机、发电机、伺服系统和调速器组成.水库上游来水经压力管道流入蜗壳，带动水轮机和发电机旋转.发电机与水轮机一般通过轴联器连接，调速器控制水轮机导叶开度来调节转速.调速系统的典型方框图如图1所示[14].

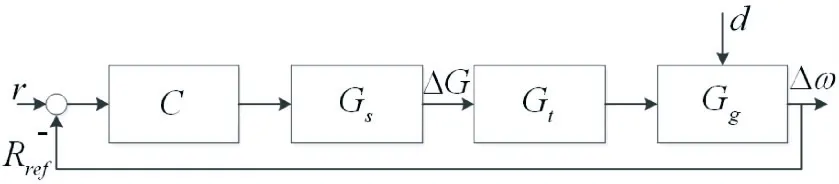
图1 水轮发电机组调速系统结构图

图1中：C(s)为系统控制器传递函数，Gs(s)为伺服系统模型的传递函数，Gt(s)为水轮机模型的传递函数，Gg(s)为发电机模型的传递函数，r是给定参考转速，水门开度偏差ΔG(s)作为提高性能的中间输出，Δω(s)是输出的发电机转速偏差，Rref为反馈，d为电网负荷变化量.

1.2 水力系统模型

水轮发电机组调速控制中，水头Ht和水在压力管道中的流速V是两个关键变量，两者之间存在关系.水锤效应是指光滑管道内水流量发生急剧变化时阀门会受到压力的效应.由于压力钢管弹性和水的可压缩性，将造成压力波在柱上传播，所以波传播时间就变得十分重要.本文讨论单管单机，则水轮机涡轮进口处水头增量与水流增速度之比为[15]：

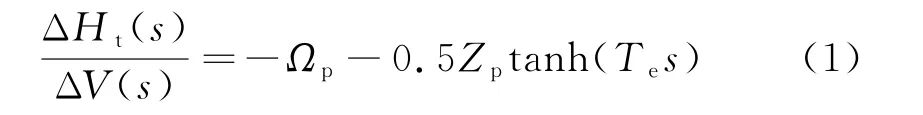
式中：ΔHt为水头增量；Ωp为压力管道的摩擦系数；Te为波传播时间.

标准压力管的浪涌阻抗Zp为：

式中：Tw为水启动时间，满足下式[16]：

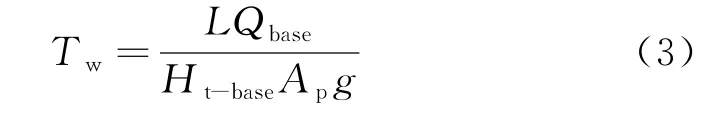
式中：L为压力管道的长度；Ap为压力管道的截面积；Ht-base为水柱水头单位基准值；Qbase为水的流速基准值；g为重力加速度；Tw是在标准水头作用下，水流流量从0增加到1所需要的时间；式(2)中波传播时间Te是压力管道长度L与水波速度a的比值，见式(4)：

式(1)中的摩擦系数Ωp取决于摩擦系数kp和水流稳态速度V0，其关系见式(5)：

式(1)中的正切双曲函数可由无穷乘积展开表示：

1.3 水轮机模型

水速度增量和机械功率增量为：

式中：ΔV为水速度增量；ΔPm为机械功率增量.

结合式(1)，(7)和(8)，考虑水锤效应、摩擦引起的水头损失和非弹性压力管道影响，水轮机模型Gt如下：

1.4 发电机模型

发电机模型如下[16-19]：

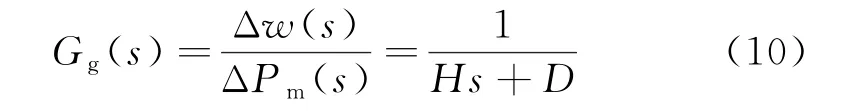
式中：H为转动惯性时间系数；D为发电机阻尼系数.

1.5 伺服系统模型

伺服系统模型如下[16-17，19-20]：

式中：Tp为伺服系统时间常数；Ts为伺服电机的时间常数.

2 水轮发电机组多回路鲁棒调速控制系统模型

由于水轮发电机组调速系统存在波传播时间、水启动时间、发电机转动惯性时间、伺服电机和伺服系统时间常数、发电机阻尼系数等多种模型参数不确定性，还有水锤效应以及来自外部负荷的干扰，因此对水轮发电机组调速系统进行多回路控制.

发电机组转速受阀门开度的直接影响，为保证电网频率稳定，将导叶开度作为第一控制回路的输出；并在第一控制回路基础上与水轮机组成第二控制回路来有效减少水锤效应；最后将第二控制回路与发电机组成第三控制回路来抑制电网负荷各类干扰.水轮发电机组多回路鲁棒调速控制系统的结构如图2所示.

图2 多回路鲁棒调速控制系统结构图

图2中：Gs(s)是伺服系统的模型传递函数；Gt(s)是水轮机模型的传递函数；Gg(s)是发电机模型的传递函数；U(s)是控制输入信号；Ux(s)是操作输入信号；ΔG(s)表示阀门开度偏差；ΔPm(s)表示机械功率增量；d表示负荷扰动输入；Δw(s)表示输出的发电机转速偏差；Rref1、Rref2、Rref3分别为控制器C1(s)、C2(s)、C3(s)的输入反馈.

为了减少水轮发电机组调速系统对参考输入信号的跟踪误差和有效抑制导叶开度干扰的影响，使用混合灵敏度方法设计控制器C1(s)第一控制回路.但是混合灵敏度方法设计不能始终保证闭环系统的鲁棒稳定性和鲁棒性能，所以引入μ综合方法分别设计控制器C2(s)第二控制回路和控制器C3(s)第三控制回路来提高闭环系统的鲁棒稳定性和鲁棒性能.

3 水轮发电机组多回路鲁棒调速控制系统设计

水轮发电机组调速系统不确定参数如下：波传播时间常数Te∈[0.2，0.5]，水启动时间常数Tw∈[0.5，4]，伺服系统时间常数Tp∈[0.005，0.02]，伺服电机时间常数Ts∈[0.05，0.5]，转动惯性时间常数H∈[4，13.2]，发电机阻尼系数D∈[0，1].标称系统取Te=0.35、Tw=2.25、Tp=0.0125、Ts=0.275、H=8.6、D=0.5.水轮发电机组调速系统模型见第一部分，模型参数见文献[19].下文对水轮发电机组多回路鲁棒调速控制系统按照不同回路依次分析.

3.1 第一控制回路分析

为了减少水轮发电机组调速系统对参考输入信号的跟踪误差和有效抑制导叶开度干扰，使用混合灵敏度方法设计第一控制回路的控制器C1(s).

该回路抗干扰能力的目标是扰动等输入的变化对输出的变化影响应尽可能小，即：

式中：‖S‖∞表示系统抗干扰能力的强弱.

该回路具有鲁棒性要求，即受控对象在受到设定范围内的摄动时仍能保持稳定的能力.可以通过使用范数界来约束R与T，即分别限制高频未建模动态及中低频参数摄动来保证鲁棒性，可表示为：

式中：‖R‖∞表示加性不确定性中不确定性大小的度量，‖T‖∞表示乘性不确定性中不确定性大小的度量.

在一定范围内，W2的选取越大会使得‖R‖∞过小，在实际设计过程中，常常将W2设定为一个常数权以获得中低频内有较好鲁棒稳定性的参数摄动范围.根据以上原则进行参数的选择并仿真，直至得到合适的权函数W1、W2、W3.

根据以上权函数选取原则，可得第一控制回路的3个权函数的值为：

通过混合灵敏度方法设计得到C1(s)：

C1(s)=(1.353×107s3+5.526×1010s2+

4.531×1012s+1.575×1013)/(s4+2.129×104s3+

1.495×108s2+3.88×1011s+5.819×1010)(18)

3.2 第二控制回路分析

为了减少水锤效应带来的不利影响，对水轮发电机组调速系统中水轮机进行控制，引入μ综合方法设计第二控制回路的控制器C2(s).

参照第一控制回路选取权函数的原则，可得第二控制回路的3个权函数值为：

通过μ 综合方法设计得到C2(s)为97 阶控制器，阶数太高不便于计算，而且可能不是很必要.对控制器降阶有时能够在不影响控制性能的前提下降低控制器的复杂性，便于计算.如果降阶至5阶及以下会严重失真，因此取6阶控制器为：

第二控制回路单位阶跃响应如图3所示.从压力管道来水时，大约在0.457s时有一个冲击作用，随后水轮机转速开始逐渐上升，标称系统可以在2.64s达到稳定状态，对于不确定系统的随机取值均可在2.64s达到稳定状态，其中红色曲线代表标称系统.

图3 水轮机单位阶跃响应图

3.3 第三控制回路分析

为了有效抑制电网负荷干扰及获得更好的闭环系统鲁棒稳定性和鲁棒性能，引入μ综合方法设计第三控制回路的控制器C3(s).

参照第一控制回路选取权函数的原则，可得第三控制回路的3个权函数值为：

通过μ 综合方法设计得到C3(s)为99 阶控制器，由第二控制回路降阶的原因可得，降阶至3阶及以下会严重失真，因此取4阶控制器为：

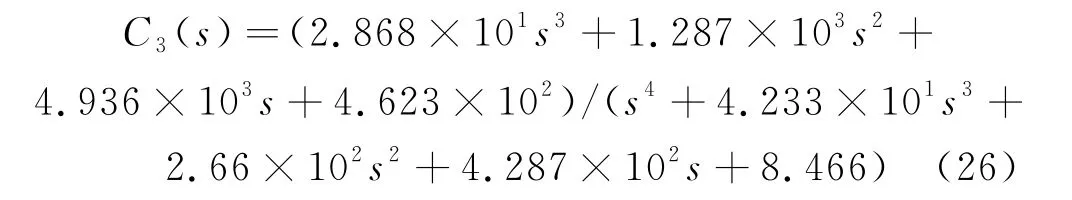
水轮发电机组多回路鲁棒调速控制系统单位阶跃响应如图4所示.

图4 多回路鲁棒调速控制系统单位阶跃响应图

从图中可知，水轮机转速达到稳定的第1.34s之后，也就是在3.59s时，整个标称系统能够达到稳定状态.系统不确定参数的随机取值均可在16.4s时达到稳定状态，其中红色曲线代表标称系统.

4 不同类型调速控制系统对比分析

将水轮发电机组多回路鲁棒调速控制系统与传统PID 单回路调速控制系统及水轮发电机组双回路鲁棒调速控制系统作对比分析.其中，传统PID 单回路调速控制系统中控制器的传递函数为[11]：

双回路鲁棒调速控制系统中控制器的传递函数为[13]：

水轮发电机组多回路鲁棒调速控制系统与传统PID 单回路调速控制系统及双回路鲁棒调速控制系统相对比的阶跃响应如图5所示，其中红色代表水轮发电机组多回路鲁棒调速控制系统的标称系统的阶跃响应.

图5 不同类型调速控制系统对比图

各个控制系统的标称指标如表1 中2～4 列所示.通过时域指标分析可知，水轮发电机组多回路鲁棒调速控制系统较传统PID 单回路调速控制系统在控制效果上有明显优势，传统PID 单回路调速控制系统在75.3s左右才能够达到稳定状态，且振荡次数较多.多回路鲁棒调速控制系统较双回路鲁棒调速控制系统在超调和振荡大致相当的前提下可以更快达到稳定状态，大约需3.59s，而双回路鲁棒调速控制系统则需7.46s才能达到稳定状态.

表1 时域指标

为保证电网频率稳定，适应电网负荷随机变化，需要水轮发电机组调速系统以最快速度来响应.本文考虑电网负荷突然增加或减少时对系统控制效果的影响.当水轮发电机组调速系统稳定后，在100s时突然增加或减少50%负荷.

分别对传统PID 单回路调速控制系统和双回路鲁棒调速控制系统进行同样的干扰测试.如图6～7和表1中5～7列所示，多回路鲁棒调速控制系统的控制效果比传统PID 单回路调速控制系统和双回路鲁棒调速控制系统能够更快地且经过更少的震荡达到稳定状态，可见在受到干扰时其也具有很好的鲁棒性能.

图6 突加50%负荷单位阶跃响应图

图7 突减50%负荷单位阶跃响应图