高压输电线路救援机器人机械臂壳体拓扑优化设计

田启华 段龙飞 周祥曼 黄佳康 杜义贤

(三峡大学 机械与动力学院， 湖北 宜昌 443002)

本文以救援机器人机械臂壳体为研究对象，先对其进行静力学分析，并在此基础上对其进行拓扑优化设计，然后综合考虑加工制造、装配等因素对其进行模型重构，最后对重构前后的模型进行力学性能的分析与比较，验证该设计的合理性和有效性.

1 机械臂壳体工况分析

救援机器人的机械结构如图1 所示，其由机械臂、夹紧机构、行走机构、刹车机构、支撑架及吊篮等组成，能实现自主越障和救援任务.

图1 救援机器人机械结构

机械臂壳体如图2所示，其总体结构尺寸为长×宽×高=100mm×100mm×510mm，质量为3.8883 kg，材料为铝合金.机械臂壳体通过连接销和滑杆将救援机器人的上下两部分连接在一起，是最为重要的受力件之一，且机械臂壳体体积大、质量重，优化空间大，因此本文以机械臂壳体为研究对象，对其进行轻量化设计.

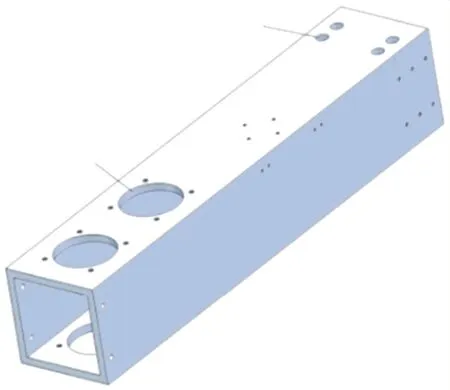
图2 机械臂壳体

救援机器人设计的有效载荷为500kg，其在线上作业时，机械臂壳体承受的拉力主要来自支撑架、吊篮和检修人员，且救援机器人在线上行走越障时无论如何至多只有一个机械臂悬空，则单个机械臂壳体所受的最大拉力F为：

式中：m1为支撑架的质量；m2为吊篮的质量；m3为检修人员的质量；α为导线的坡度；g为重力加速度；r为安全系数.

2 拓扑优化数学模型的建立

在对连续体结构进行拓扑优化时，变密度法是最常用的方法之一，因此本文采用变密度法对机械臂壳体进行拓扑优化设计.变密度法的基本思想是人为假设材料单元的密度是可变的，并假设这种材料单元的密度与材料的物理属性之间存在某种函数关系，根据以上假设建立材料模型，以材料密度的分布情况来确定结构材料的布局情况.但在使用该方法时会出现大量的中间密度材料单元，这显然是不希望看到的，因此通过SIMP法引入惩罚因子p，使材料的中间密度值向0和1两端聚集，从而得到最终的优化结果[9-10].

结合载荷与位移边界条件，可得到基于SIMP法的结构拓扑优化模型为：

式中：ρ为拓扑设计变量；Xe为每个单元的相对密度；ρi为每个单元的固有密度；Ke为单元的刚度；Ki为单元的固有刚度；p为惩罚因子.当Xe=1时，保留结构的材料；当Xe=0时，去除结构的材料.

以机械臂壳体总体柔度最小为目标函数，则机械臂壳体的拓扑优化数学模型[11-12]为：

式中：目标函数C为机械臂壳体的总体柔度；F为载荷矢量；U为结构位移向量；K为优化前结构总刚度矩阵；M为充满材料的体积；M0为结构设计域的体积；M1为密度小于1的材料体积；f为剩余材料百分比；Xmin为单元相对密度的下限；Xmax为单元相对密度的上限.

3 机械臂壳体拓扑优化设计

3.1 静力学分析

以现有的外型尺寸为起点进行优化设计.在进行网格划分之前先对结构进行适当简化，清理掉一些不影响分析结果的螺栓孔、倒圆角等，使用SolidWorks构建的机械臂壳体原始模型如图3所示.铝合金弹性模量为E=7.1×104MPa ，泊松比μ=0.33，密度ρ=2.8×103kg/m3，采用ANSYS Workbench智能网格划分技术对该模型进行网格划分，其中关联性为100，单元大小为2 mm，得到459404 个节点和276466个单元.

图3 机械臂壳体原始模型

对连接销孔施加固定约束(Fixed Support)，对滑杆孔施加轴承载荷(Bearing Load)[13].经分析可得，当导线的坡度为0时，机械臂壳体受到的拉力最大，最大为3000N.机械臂壳体施加的载荷与约束如图4所示.

图4 机械臂壳体载荷与约束

静力学分析结果如图5所示.通过对机械臂壳体进行静力学分析求解运算可得，当拉力最大时，机械臂壳体的最大应力为6.0509MPa，位于滑杆孔两侧的表面上，如图5(a)所示，最大变形量为0.010342 mm，位于滑杆孔的下方，如图5(b)所示.由图5分析可知，基于经验设计的机械臂壳体的强度与刚度均足够，能够满足救援机器人的实际工作需求，但机械臂壳体有很大部分所受应力及变形都比较小，材料冗余量较大，存在很大的优化空间.

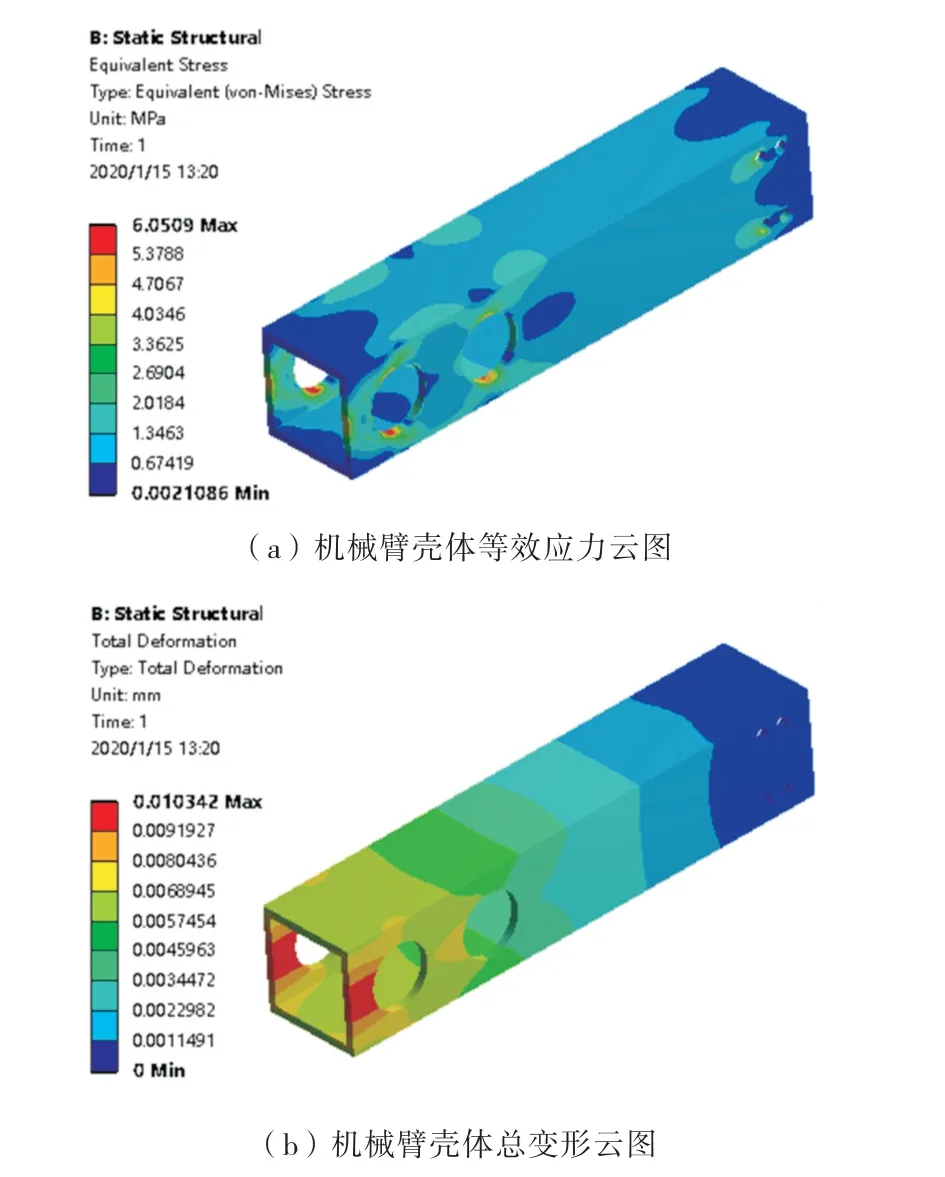
图5 机械臂壳体重构前静应力分析

3.2 拓扑优化设计

本文在Static Structural模块基础上调用Topology Optimization模块对机械臂壳体进行拓扑优化.合理有效的参数设置才能得到更佳的优化效果，因此在优化前先对设计参数进行设置，见表1.

表1 优化设计参数设置

参数设置后执行迭代计算，机械臂壳体拓扑优化结果如图6所示，其中透明部分表示可去除材料，从图中可以看出，可去除材料多分布在滑杆孔的上方及滑杆孔的左右两侧(以图1中机械臂壳体装配状态下的方位来进行观察).

图6 机械臂壳体拓扑优化结果

根据拓扑优化结果并综合考虑加工制造、装配等因素对机械臂壳体进行重构.重构时保留具有特定作用的部分，如图7所示.对重构后的模型再进行静力学分析，得到应力及变形云图如图8所示.

图7 机械臂壳体重构后模型

图8 机械臂壳体重构后静应力分析

从图8 可以看出，机械臂壳体最大应力为8.7145MPa，远小于材料的抗拉强度.最大变形量为0.018015mm，也满足设计要求.重构后机械臂壳体的质量为2.2787kg，减轻了41.40%.结果表明重构前后的模型在最大应力与最大变形相差不大的情况下质量减轻了许多，从而达到了减重的目的.

4 结 论

1)针对机械臂壳体经验设计的不足，应用ANSYS Workbench对其进行拓扑优化，确定了机械臂壳体的可优化区域，为机械臂壳体的减重设计提供了一种科学依据.

2)在拓扑优化的基础上，综合考虑机械臂壳体的装配、加工制造及配件的安装等因素，对机械臂壳体进行了重构，大大减轻了机械臂壳体的重量.通过对重构前后机械臂壳体的静力学分析，结果表明该重构模型满足实际工况需求，达到了减重的目的.

3)该优化方法对救援机器人的其他结构及同类型结构的优化具有一定的参考价值，同时救援机器人质量的减轻可有效减少运输过程中人力物力资源的浪费，为救援工作赢得宝贵时间.