锂离子动力电池组发热功率试验研究
2020-06-02王明强郭月明许淘淘方勇
王明强,郭月明,许淘淘,方勇
(中航锂电(洛阳)有限公司,河南洛阳 471003)
0 引言
近年来,电动车辆发展迅猛,动力电池作为电动车辆的关键部件,在技术上也得到了快速发展。锂离子动力电池以其能量密度高、比功率高、寿命长、自放电率低以及存储时间长等优点,成为电动车辆首选动力来源。而受政策、市场等方面的影响,具有高能量密度的三元锂离子电池应用越来越广泛。锂离子电池作为电动车辆动力输出的主要能量来源,其放电容量、工作电压、循环寿命以及状态一致性等都与电池的工作温度密切相关[1],因此对锂离子电池的性能研究及热管理系统设计开发具有重要意义。
目前,广泛使用的电池生热模型为Bernardi方程[2],该模型是基于电池内部产热均匀的假设提出的,方程计算简单。文献[3]中建立了方形锂离子单体电池的三维热模型,文献[4]和文献[5]中建立了方形锂离子电池组的三维热模型,模型可用于电池组、热管理系统结构细节方面的改进,但其计算复杂。文献[6]和文献[7]中在考虑极片中参数空间差异的前提下建立了锂离子电池的热模型,模型中均忽略了电池内生成的可逆热。但相关研究表明,可逆热约占锂离子电池内部产生的全部热量的30%[8]。
本文作者通过理论产热计算和试验测试对电池模组的发热功率进行研究,通过对比验证理论产热模型的准确性,并通过CFD软件对所设计的电池模组进行热仿真分析,将仿真结果与试验结果进行对比,验证模拟分析的有效性及模拟精度。
1 电池发热功率理论计算
锂离子动力电池充放电过程中,其内部发热量主要来自于内阻产生的欧姆热和化学反应热。D BERNADI等基于电池内部产热均匀的假设提出了目前较为常用的锂离子动力电池发热功率计算公式:
(1)
以上三项分别表示不可逆内阻热、可逆熵热和混合热。随后THOMAS和NEWMAN证实:在电池的设计过程中,如果减小极化浓度差,混合热也可以忽略不计。公式(1)可以简化为
(2)
式中:E为电池在平衡状态下的开路电压,V;U为电池工作电压,V;I为电池工作电流,A,充电取正,放电取负;T为电池温度,K;E-U=IR,R为电池总内阻,包括欧姆内阻和极化内阻,Ω。
对锂电池在不同温度下进行1C充放电,SOC为50%时,试验测试得电池的工作电压、开路电压及直流内阻如表1所示。
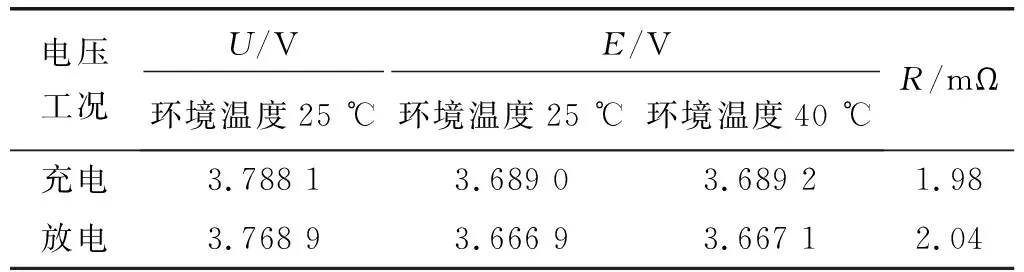
表1 不同温度下锂电池工作电压和开路电压
结合表1和公式(2)可计算得到单体电池及电池模组1C充放电过程中,50%SOC状态下的发热功率,如表2所示,其中,模组为3并4串,共12支电池。

表2 电池充放电发热功率 W
由以上计算结果可知,当三元锂离子电池进行1C充放电试验,50%SOC时,充电发热功率略小于放电发热功率。
2 电池发热功率试验测试
2.1 试验设备
试验所需设备包括:三元锂离子动力电池模组、充放电设备、液冷机及冷却液管路、温度记录仪、数据采集系统。试验过程中需要对模组进行绝热保温,如图1所示,此试验共对电池模组设置泡沫板、纸箱和保温棉三层保温。

图1 电池模组保温设置
2.2 试验对象
试验研究对象为三元锂离子动力电池模组,电池模组由12支单体电池通过3P4S的形式连接在一起,单体电池标称容量为50 A·h,电池单体及模组三维模型如图2所示。

图2 电池单体及模组
2.3 试验方案
图3为电池模组发热功率测试试验系统图,按照图示连接试验设备,调整模组SOC为50%,在室温下静置20 h后将电池模组进行绝热保温包裹;以 150 A 恒流充电10 s,再以150 A 恒流放电10 s,重复该恒流充放电循环,同时开启液冷,设置冷却液(体积分数50%的乙二醇水溶液)入口流量为1.25 L/min,入口温度为20 ℃;当电池模组温度不再变化(即各温度采集点的温度变化率小于0.5 ℃/30 min),试验停止,试验过程中记录冷却液进出口温度、流量。试验过程中,模组温度采集点布置如图4所示。
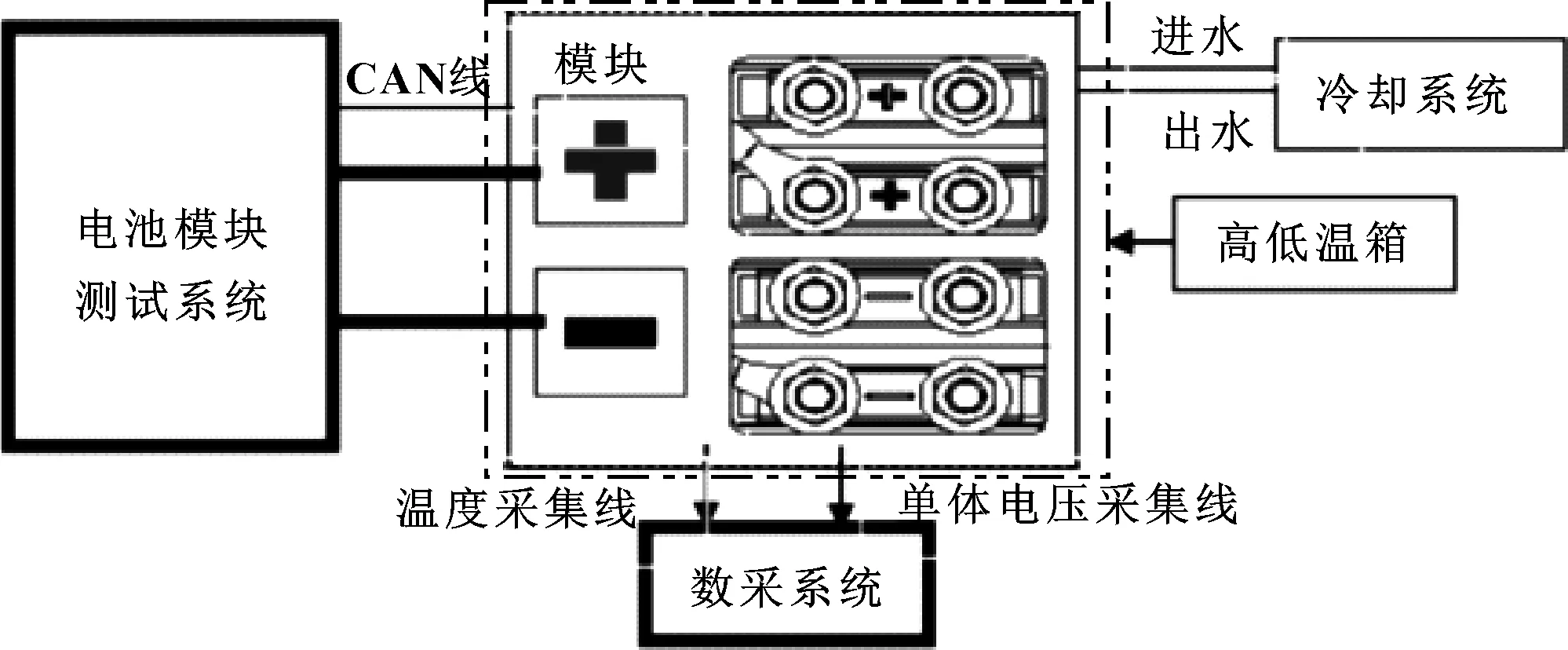
图3 电池模组发热功率测试试验系统图

图4 试验过程中模组温度采集点布置
2.4 试验结果及分析
图5反映了在150 A(1C)循环充放电过程中,电池模组顶部的温度分布情况。随着循环充放电的进行,模组顶部温度逐渐升高,温升速率逐渐降低,温度曲线最终趋向平稳。当模组顶部6个温度采集点最大温度变化率为0.1 ℃/30 min,试验停止。试验结束时,模组顶部最高温度为34.3 ℃,位于1号温度点,最低温度为33.0 ℃,位于6号温度点,温度点之间最大温差为1.3 ℃。
图6反映了在150 A(1C)循环充放电过程中,电池模组底部的温度分布情况。模组底部温度随着循环充放电的进行有短暂的快速降低后缓慢升高,最终趋向平稳。模组底部温度快速降低是由于当试验开始刚通入20 ℃冷却液时,模组底部迅速通过铝质液冷板向冷却液传递热量Q1,温度快速降低。降低到最低点后又缓慢升高是由于随着充放电的进行,模组顶部温度升高,热量Q2向模组底部传递,当Q2=Q1时,底部温度达到最低,但此时Q2小于模组自身发热量Q,模组顶部温度仍继续升高,使得Q2继续增大,而当Q2>Q1时,模组底部温度开始升高;随着模组底部温度的升高,Q1也开始增大,直到再次Q1=Q2=Q时,模组温度整体达到稳定。图中锯齿形波动是因为冷却液流量较小,冷却液温度不稳定。试验结束时,模组底部最高温度为30.2 ℃,位于7号温度点,最低温度为28.0 ℃,位于12号温度点,模组底部最大温差为2.2 ℃。
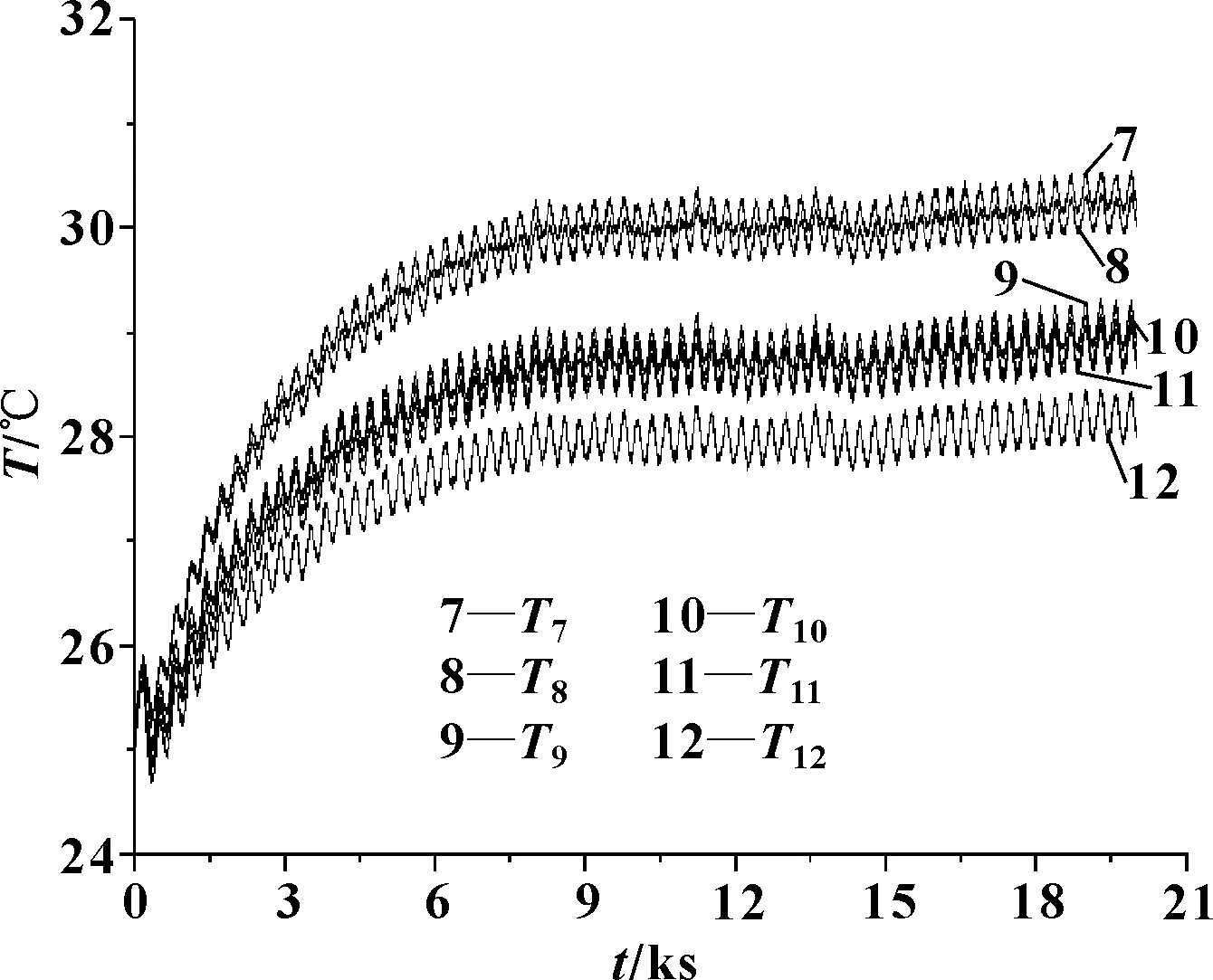
图6 试验过程中电池模组底部温度分布
图7反映了在电池模组在150 A (1C)循环充放电过程中冷却液进出口的温度变化。初始阶段冷却液温度由25 ℃(室温)快速降低至21 ℃附近,随着试验的进行稳定在21 ℃并呈锯齿形周期性波动,这是因为液冷机流量太小,温度调整具有一定的滞后性。
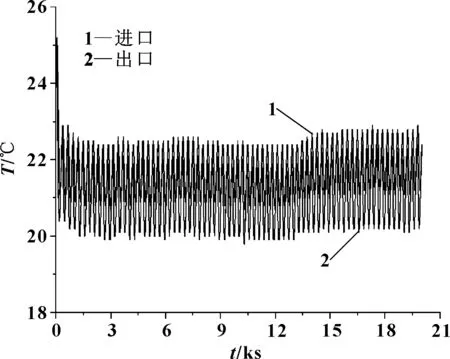
图7 试验过程中冷却液进出口温度
试验结束时,模组顶部、底部及冷却液进出口温度如表3所示。

表3 试验结束时模组及冷却液温度
备注:由于冷却液进、出口温度有较大波动,在对冷却液进、出口温度进行数据处理时,分别取试验结束前30 min整周期的平均值作为进出口温度进行温差计算。
从表3可以看出:在试验结束时,模组顶部最高温度为34.3 ℃,模组底部最低温度为28.0 ℃,最大温差为6.3 ℃,结合冷却液进出口温差,电池模组发热功率按下列公式进行计算
(3)
式中:Q为模组发热功率,W;c为冷却液比热容,J/kg·K;L为冷却液体积流量,L/min;ρ为冷却液密度,kg/m3;Δt为冷却液进出口温差,℃。
冷却液的物性参数可以通过查表得到,代入数据得:
与第1小节理论计算所得的模组发热功率相比,二者之间的误差为
3 电池充放电温度场模拟
3.1 物理模型
仿真分析模型与试验相同(图8),包括电池模组和液冷板,生成网格数为92万。

图8 模组及液冷板三维数模
3.2 控制方程
由于电池内部复杂,为便于进行仿真计算,对电池模组进行如下简化假设:电池内部材料各向同性,物理性质均一,且各项物性参数不随温度、时间变化;电池为均匀发热体;忽略电池内部的对流和热辐射,热量的传递为稳态三维导热;忽略电池与周围环境的对流换热。基于以上假设,电池模组能量控制方程为
(4)
式中:ρ为电池密度,kg/m3;Cp为电池比热容,kJ/(kg·K);λi为电池在i方向上的导热系数(i=x、y、z),W/(m·K);Φ表示电池发热功率,W;Φ′表示散热功率,W。
3.3 边界条件及初始条件
参照第2节试验工况,设置模拟环境温度为25 ℃,液冷板进出口冷却液流量为1.25 L/min,进水温度为21 ℃,电池按1.0C循环充放(20 s一个周期),电池模组总发热功率60.3 W,三维数模与环境接触面设置为绝热壁面。
3.4 模拟结果及分析
当迭代计算t=3 000 s时,结果收敛,得到电池模组温度场分布如图9所示。

图9 模拟电池组温度场分布
从图9可以看出:由于模组底部设置液冷板,模组温度从上到下依次降低,呈现一定的温度梯度。电池模组极柱最高温度约为33.9 ℃,最低温度约为32.9 ℃,二者相差1 ℃,且模组顶部极柱温度最低点位于靠近冷却液进口处的单体电池,极柱温度最高点位于靠近冷却液出口处的单体电池,这是由于冷却液吸收热量后温度升高导致的。将模拟仿真数据与试验数据对比如表4所示,可以看出:二者之间的误差约为9.5%。所以认为该模拟仿真结果精度较好,可对前期热管理设计提供一定的参考价值。

表4 模拟仿真数据与试验数据对比
4 结论
本文作者通过理论计算、试验研究与仿真分析的方法对三元锂离子动力电池发热功率进行了研究,得出结论如下:
(1)按Newman公式进行理论计算所得电池模组发热功率与试验测得模组发热功率误差为8.7%,试验测得发热功率低于理论计算值;
(2)按理论计算电池模组发热量对电池模组进行底部带液冷板模拟仿真,结果表明:模拟收敛后电池模组最高温度和最低温度与试验结果比较接近,二者之间的误差约为9.5%,该模拟结果可对电池热管理设计提供一定的参考价值;
(3)通过理论计算、试验研究与仿真分析三者之间的对比,Newman公式可以用于电池模组发热功率计算,依此计算结果进行模拟仿真,结果误差较小。
