某扭转梁扭转疲劳工况应力分析以及结构优化

2020-06-02梅一丹薛仁杰郁呈祥施宇峰熊文文

汽车零部件 2020年5期

梅一丹，薛仁杰，郁呈祥，施宇峰，熊文文

(中汽研汽车零部件检验中心(宁波)有限公司，浙江宁波 315104)

0 引言

一般车辆的悬架零部件损坏大多是由于结构疲劳失效引起的[1]。在悬架零部件设计过程中，要对零件的结构和功能进行耐久性分析。而悬架零部件耐久性验证方法主要有：整车道路试验，实验室道路模拟试验，其中实验室道路模拟试验又分为零部件的单独台架试验和路谱迭代整体台架试验。单独台架试验是用标准的试验工况来模拟等效试验场路试对零部件所造成的疲劳损伤，其优点在于针对性强、周期短等。

在后悬架的结构中，扭转梁结构因具有质量轻[2]、成本相对低、车辆布置方便等特性而被广泛采用。扭转梁总成一般由横梁、横梁加强板、减振器支架、弹簧座、套管、衬套、法兰板、纵臂内外板、稳定杆等组成，详见图1。

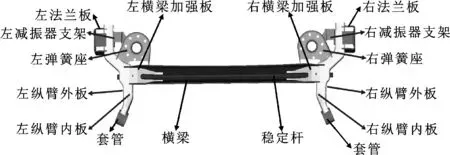
图1 扭转梁结构示意

1 扭转梁耐久试验方法

扭转梁的主要功能是在后轮与车架之间传递力和力矩，其结构尽管简单，但是受力情况复杂，左右轮心作用相互间影响。扭转梁疲劳耐久试验典型工况有扭转疲劳工况、纵向疲劳耐久工况、侧向力疲劳耐久工况，详见表1。

表1 某扭转梁疲劳耐久试验标准

其中扭转疲劳工况是扭转梁耐久试验中条件最苛刻、受力变化最大的一项试验，其加载示意图见图2。试验过程中重点关注的易出现裂纹区域，见图3。

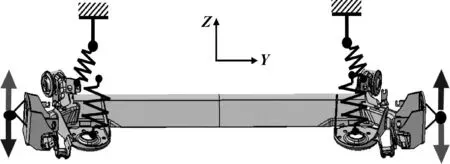
图2 扭转疲劳工况示意

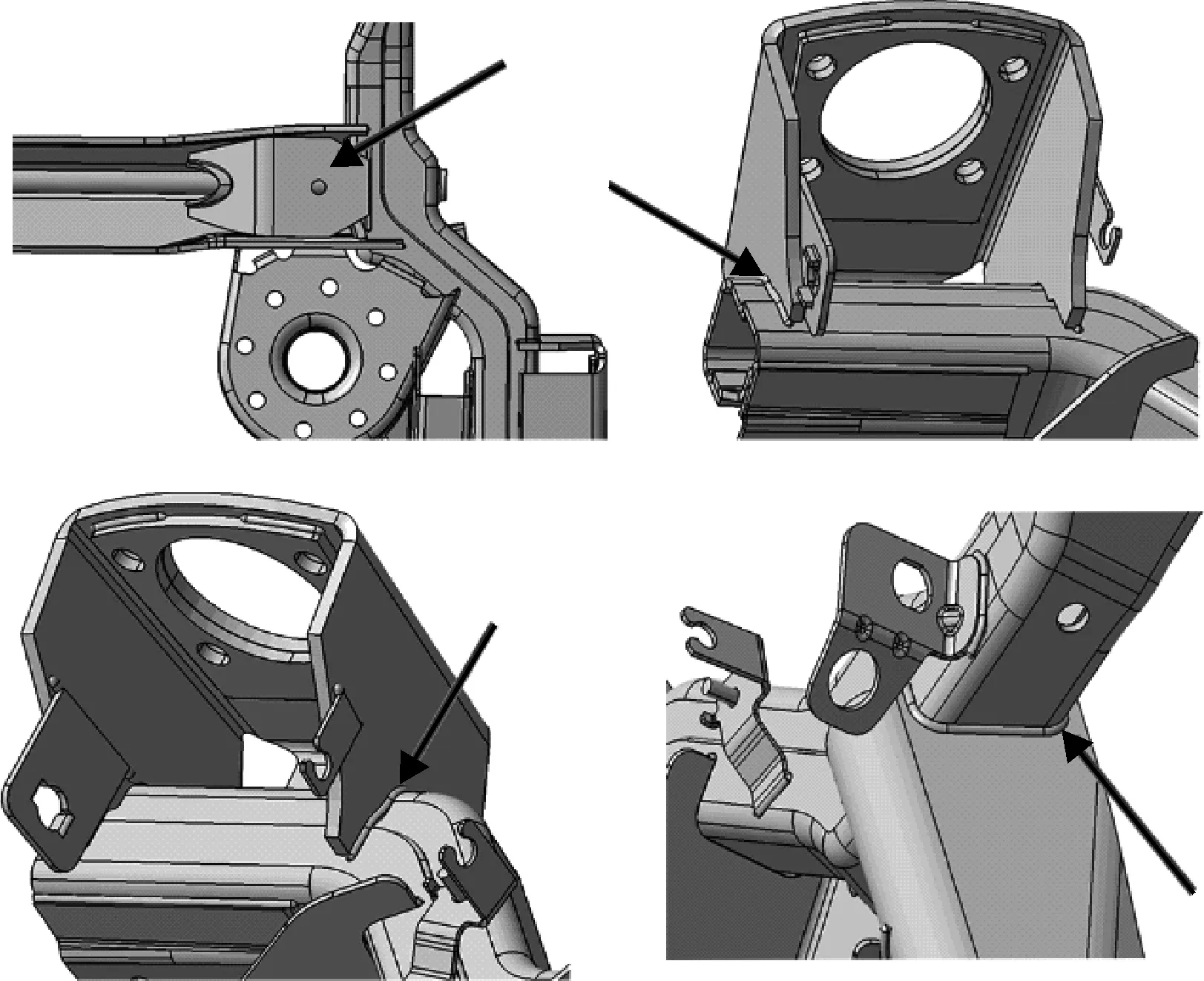
图3 扭转疲劳重点关注区域

2 开裂问题分析

某扭转梁在扭转疲劳试验进行到85 200次时，横梁右加强板的点A出现裂纹，进行到93 000次时，横梁右加强板的点B出现裂纹，见图4。该样品设计标准要求在扭转疲劳工况下，耐久次数要达到50万次，故不能满足标准要求。初步分析该横梁加强板强度不足，横梁右加强板的点B在点A出现裂纹后，迅速开裂，因为点A开裂后，点B的应力急剧上升。

图4 扭转梁裂纹位置示意

3 扭转梁结构优化

3.1 有限元建模

扭转梁采用CATIA建模，主要组成部件的材料牌号及厚度信息见表2，材料物理性能参数见表3。扭转梁总成有限元数模使用HyperMesh来构建。稳定杆使用六面体实体单元。扭转梁的其他零件采用壳体单元[3]，其中三角形单元的数量少于单元总数量的1%。应力风险位置不能有三角形单元。焊缝用壳单元模拟，采用Volvo方法建模。单元特征尺寸为 5 mm，模型单元数量为16.5万。分析中考虑了结构变形的几何非线性。

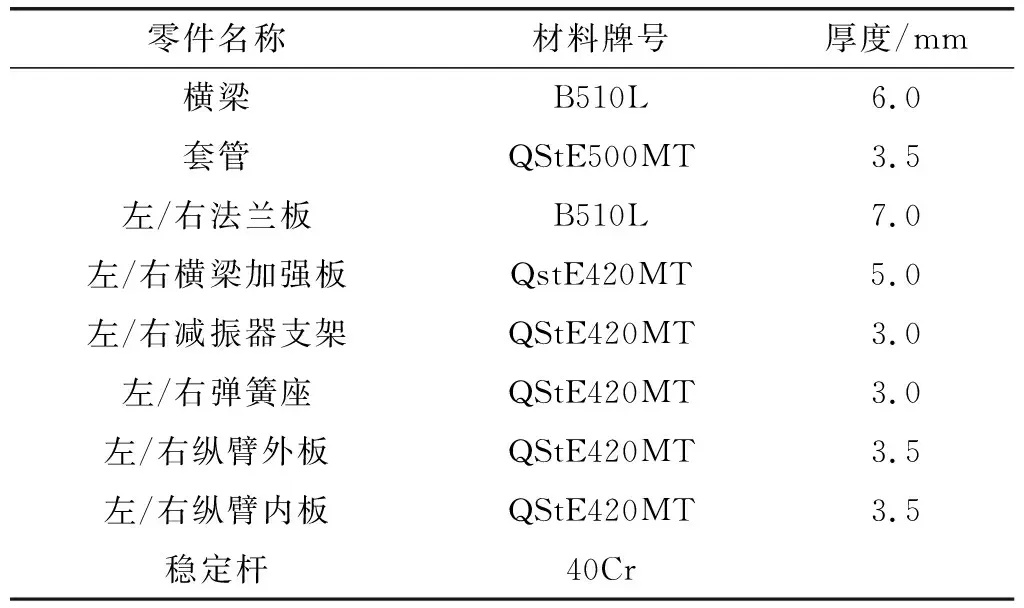
表2 扭转梁零件牌号及厚度参数

表3 扭转梁材料物理性能参数

使用ABAQUS做求解器，对扭转疲劳工况进行静力学强度分析[4]，得到后处理结果。

通过分析，在扭转疲劳工况下点A最大应力264 MPa，点B最大应力231 MPa。

3.2 结构改进优化

从图5可以看出，横梁加强板上A、B两点局部应力非常大。结构局部疲劳开裂导致产品整体失效，需要对横梁加强板进行结构疲劳优化，避免结构上局部应力过分集中，尽量使结构上的应力比较均匀[5]，从而使结构不同位置的疲劳寿命比较均衡。

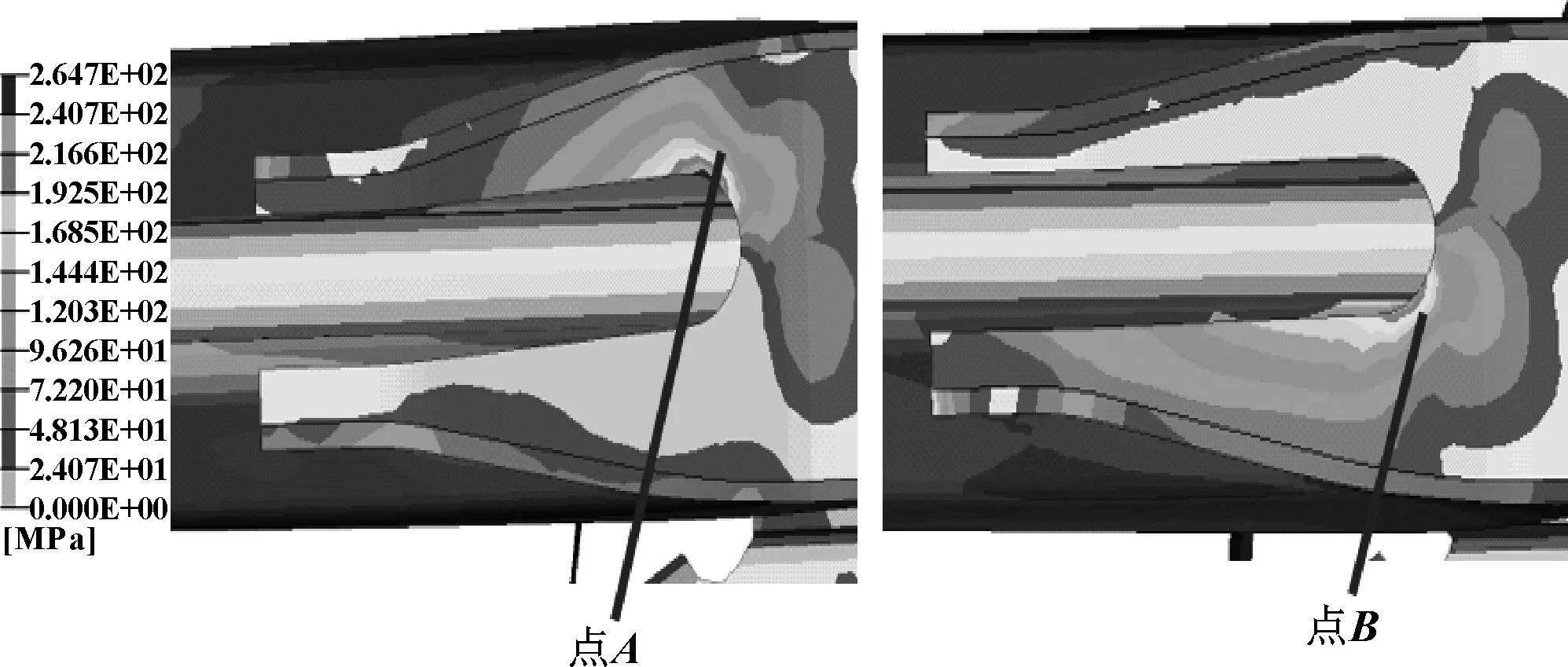
图5 失效部件最大应力示意

优化措施为：减小横梁加强板开口长度，调整加强板开口处切边过渡弧段的曲率半径，防止应力集中，达到增加结构疲劳强度的目的。横梁加强板开口处切边过渡弧段经过了若干次反复的细微调整与分析验算，调整横梁加强板的开口处的切边形状。最终横梁加强板优化方案如图6所示。

图6 横梁加强板优化后结构示意

优化后的横梁加强板开口边处应力相对较大，但应力大小比较均匀。仿真分析后点C的最大应力为195 MPa，见图7。

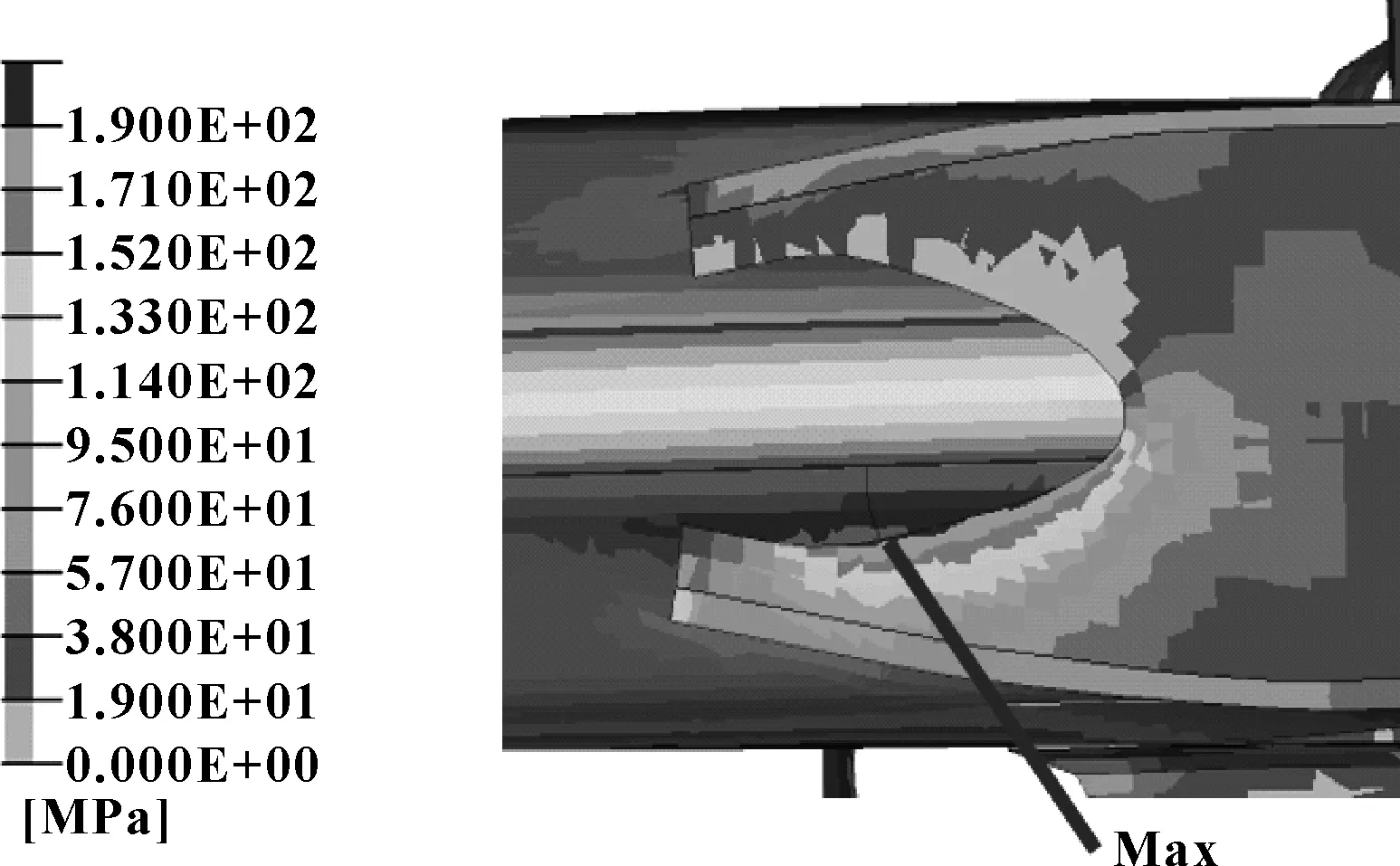
图7 点C最大应力示意

针对修改后的扭转梁，分析纵向疲劳工况和侧向力疲劳工况的最大应力状况，详见图8、图9。可见：纵向疲劳工况下，最大应力为234 MPa；侧向力疲劳工况下，最大应力为236 MPa。横梁加强板优化后几乎不对这两种工况的扭转梁寿命产生影响。

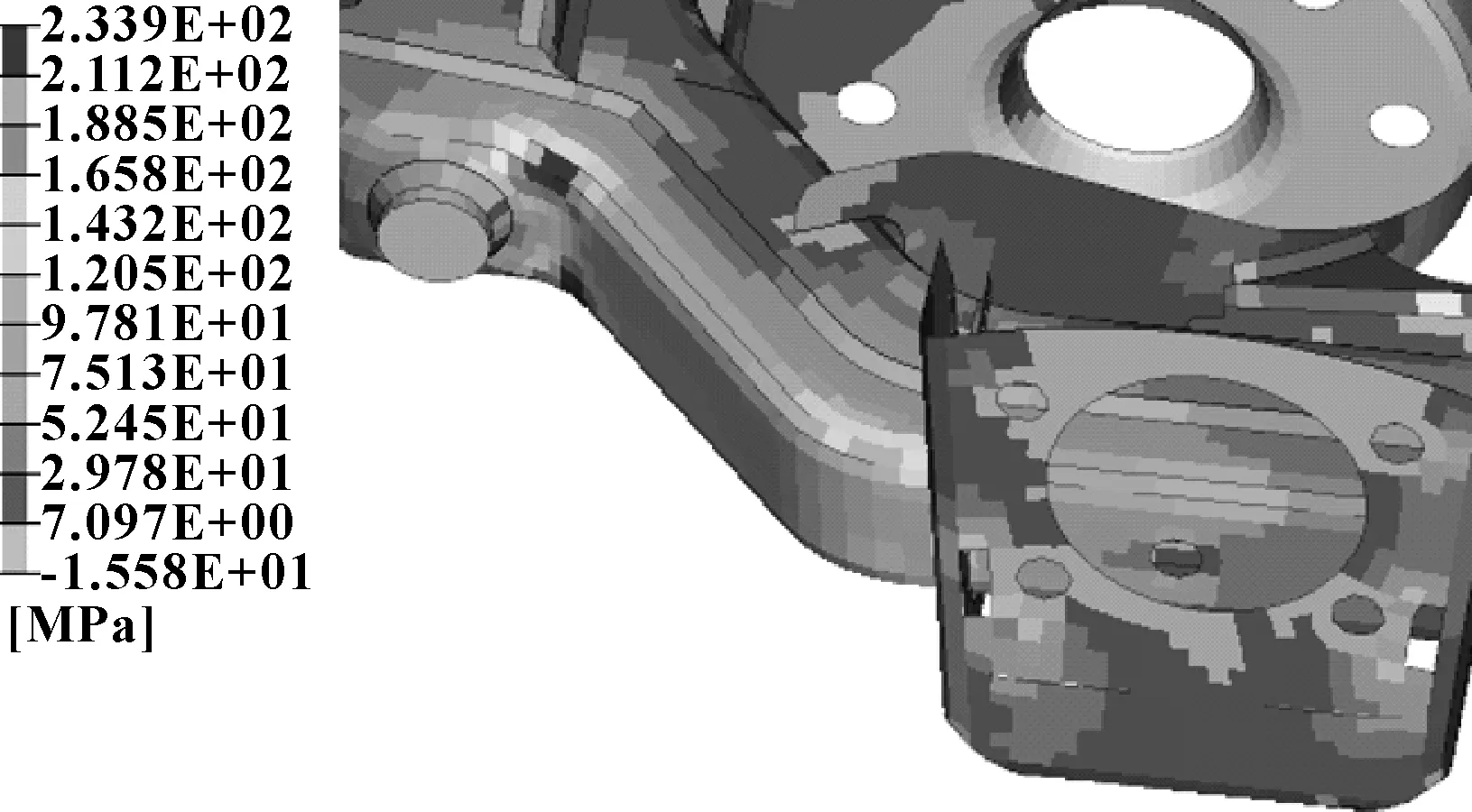
图8 纵向疲劳工况最大应力点

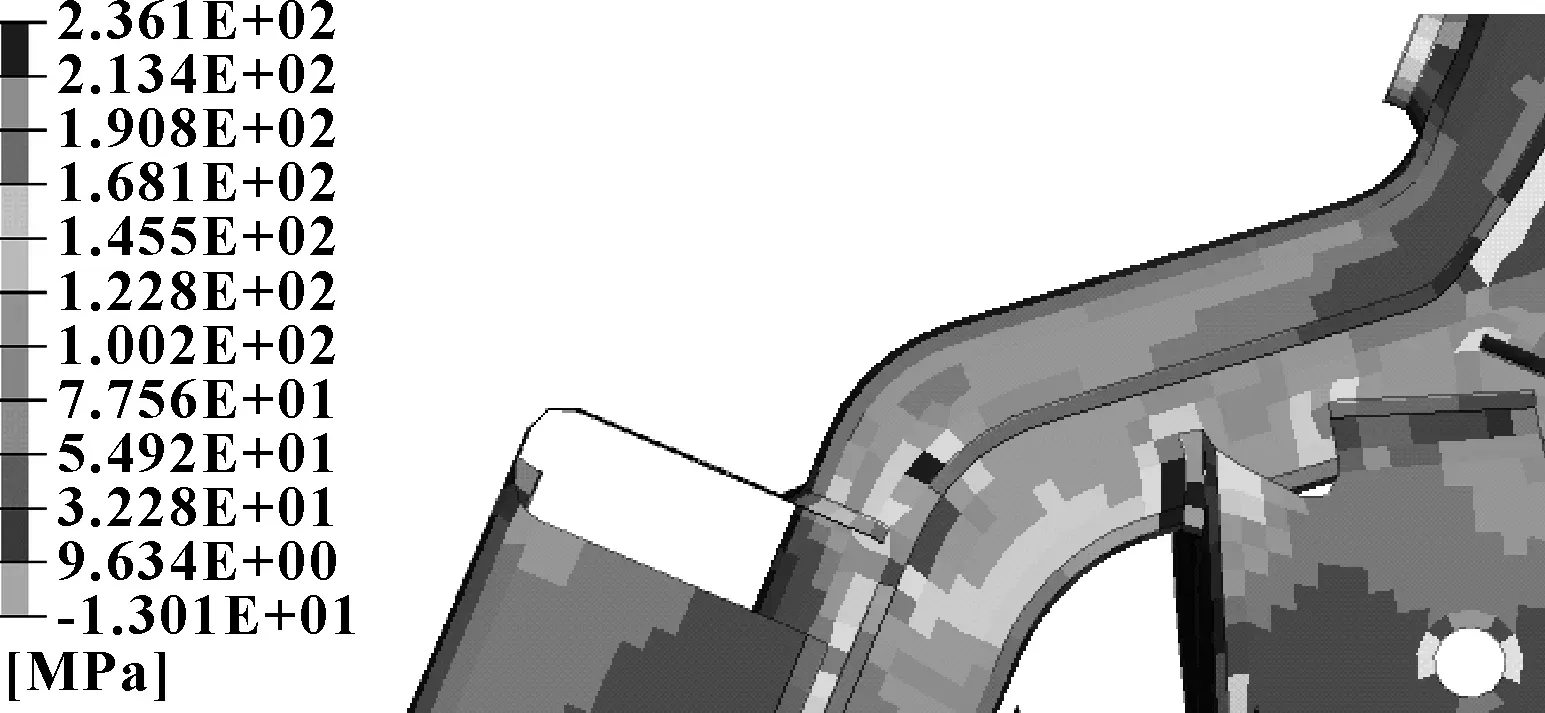
图9 侧向力疲劳工况最大应力点

4 疲劳寿命验证

4.1 台架试验验证

制作优化后的扭转梁，分别进行疲劳耐久试验验证。

扭转疲劳台架试验照片见图10，优化后的扭转梁在扭转疲劳试验进行到630 000次时横梁加强板出现裂纹，见图11，满足50万次疲劳试验要求。纵向疲劳试验进行到180 000次时纵臂外板出现裂纹，满足12万次疲劳试验要求。侧向力疲劳试验进行到95 000次未出现裂纹。

图10 扭转疲劳试验台架照片

图11 优化后的横梁加强板裂纹示意

该方案成本低，仅对现有加强板的模具进行更改，在产品开发后期更具有可行性。后期进行的整车道路试验中，扭转梁未出现开裂现象，证实该结构优化可行。

4.2 材料S-N曲线在疲劳寿命试验中的应用

结合文中的疲劳试验结果以及应力分析数据进行分析可以积累材料的疲劳性能数据，初步绘制出QStE420MT材料的S-N曲线。具体计算如下：在双对数坐标下，以寿命为横轴，以应力幅值为纵轴，在该坐标系上取两点(即是优化前点A与优化后点C的疲劳寿命以及对应的计算应力)，一点为(85 200,264)，另一点为(630 000,195)，将这两点直线连接得到近似的S-N曲线。分析纵向疲劳工况最大应力234 MPa，出现在纵臂外板处，因材料相同，按照S-N曲线预测疲劳寿命为17.8万次，跟实际试验的18万次出现裂纹试验结果非常接近。出现差异的原因是因风险位置位于材料的非边界区域，而材料的非边界区域比边缘有更好的疲劳性能。

Miner准则给出了材料疲劳损伤线性累计的一个假设。即:(1)经过特定载荷的疲劳循环加载后，材料中会出现损伤(对于单一幅值的载荷而言，损伤=1/疲劳寿命)。当损伤达到1的时候，材料疲劳失效，损伤小于1，材料尚未疲劳失效；(2)材料承受不同幅值的疲劳载荷时，材料的损伤等于各种载荷分别产生的损伤之和。

当应力幅值为264 MPa时(大载荷)，材料的寿命为85 200次，即每经过一个载荷循环，材料的损伤为1/85 200(经过85 200次，损伤达到1，材料疲劳失效)；应力幅值为195 MPa时(小载荷)，寿命为630 000次，即每经过一个载荷循环，材料的损伤为1/630 000(经过630 000次，损伤达到1，材料疲劳失效)；如果经过5万次大载荷和6万次小载荷，损伤为50 000/85 200+60 000/630 000<1，未疲劳失效。同理，85 200次大载荷与630 000次小载荷产生的疲劳损伤是等效的。可见在大载荷工况下，试验的次数少很多，可以节省大量试验时间与资源。

根据S-N曲线与Miner准则，可得到非常实用的结果。如可得出任意恒定幅值载荷对应的材料疲劳寿命；可通过损伤叠加，得到幅值变化的载荷产生的疲劳累计损伤；可以根据损伤相同的原理，制定疲劳寿命加速方案(变小载荷为大载荷，试验次数相应减小)。