基于CATIA二次开发的微透镜阵列仿真

2020-06-02严敉平

汽车零部件 2020年5期

严敉平

(常州星宇车灯股份有限公司，江苏常州 213003)

0 引言

汽车灯具的发展日新月异，近年来出现的新型灯种Logo灯逐渐流行。Logo灯可以根据客户要求将图形投射至地面，比较常见的是安装在车门上的Logo灯可在车门下方投射出公司标志，起到迎宾的效果。另一些前沿的科技中Logo灯也被集成进大灯作为超小型投影仪使用，在车辆行驶过程时可以向其他交通参与者发出警告的信息，产生双向的交互。例如迈巴赫S级的大灯可以在地面投射出诸如前方修路、雪天路滑、车距保持、行人斑马线等标识，为道路安全提供保障。图1给出了一个实例。

图1 AMS微透镜阵列MLA数字灯光[1]

Logo射灯虽然种类众多，但其基本结构和原理大致相同，即光源发出的光通过图案灯片形成形状后经过灯内的成像透镜投影至地面形成图像。与安装在车门的Logo灯不同，安装在车前侧的Logo灯光线是倾斜地投射至地面的，光型会被拉伸产生畸变，因此设计时需要对光源的图像进行修正避免失真。

CATIA是汽车行业的首选辅助设计软件，CATIA的二次开发接口和开放式的内部命令集合可用于解决各专业领域问题。本文作者具体介绍了一种在CATIA平台上开发的用于微透镜阵列仿真的程序。开发此程序的目的是对Logo灯中的光源原像进行快速设计。

1 原理概述

图2所示的Logo灯内关键部件包含光源、图案灯片和成像透镜。光线经由光源发出，通过聚光透镜聚光后打在图案灯片上，灯片是一块金属制刻上了镂空图案的薄板，光线穿过镂空部分形成图案，最后由成像透镜投影至屏幕形成最终图像。其中灯片位于凸透镜的1倍焦距和2倍焦距之间，因此屏幕上的像是倒立放大的实像。

安装在车辆前侧的Logo灯由于成像透镜与地面屏幕并不是平行关系，地面也可能是曲面。光线倾斜地投射至地面时，图形被拉伸产生畸变，得到的图像就失去了原有的形状。另一方面地面图像的远端部分由于距离光源较远，因此会比近端更暗，造成了亮暗不均。为了解决以上问题，Logo灯中布置了若干个彼此呈阵列式排布的微透镜，使各自投射出的图像产生重叠，通过对微透镜阵列进行配置，使更多的光投射至图像的远端部分，从而使得到的图像均匀性更好。此外光学设计时需要对光源的原图进行修正，才能保证倾斜投影时光线不会扭曲失真。

图2 Logo灯原理[2]

图3 微透镜阵列在车前Logo灯的应用

2 建模

对整个机构进行建模时要尽可能地考虑简化模型。为了便于介绍，以下将光源灯片上的原始图像简称为“原像”或“灯片”，将投影至地面的图像简称为“投像”。由于Logo灯中光源灯片位于透镜焦距的1倍到2倍之间，此时投像为倒立放大实像，这种情况下透镜成像的效果与小孔成像一致，对原像进行计算时可以将微透镜等效为小孔，用点来表示。

2.1 建立坐标系

原像、透镜以及投像分别形成3个平面，即原像平面、透镜平面和地平面，以这3个平面为xy平面分别定义坐标系A0、A1、A2,如图4所示。将A0定义为全局坐标系，A1、A2为局部坐标系。其中坐标系A1总以当前透镜点为原点。

由于各平面采用不同的坐标系，计算时需要进行坐标系的转化，两轴系间的转化要用到变换矩阵。变换矩阵可能是平移或绕三轴的自转：

平移矩阵：

(1)

其中：d是平行移动的方向矢量：

(2)

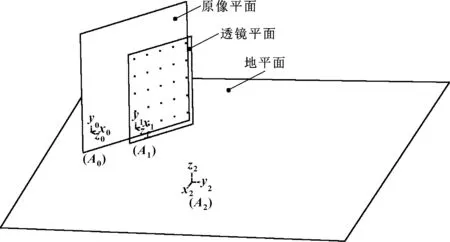
图4 建立空间内模型

绕x向旋转θ的旋转矩阵(遵循右手定则，逆时针为正，以下同理)：

(3)

绕y向旋转φ的旋转矩阵：

(4)

绕z向旋转ω的旋转矩阵：

(5)

2.2 数字化投像

投像是指位于车辆前方投影至地面的图像，以图5所示的投像内容为例(假定地面为平面，不考虑曲面)。

图5 投像内容

对图片进行计算首先要对图像进行数字化处理，图片中对计算有用的部分是图案的边界，即由一些曲线或直线围成的外轮廓。直线是能直接计算的，而对于曲线则需要采样简化。Douglas-Peucker算法是专门处理曲线离散化问题的方法，原理是在曲线上取有限个点，将其变为折线，并且能够在一定程度上保持原有的形状。文中不多介绍此算法的详细步骤，在CATIA中用户只需将CATDrawing格式的2D文件转化成Dwg格式就可以实现实心图案到空心图案的转化，然后通过右键隔离功能将曲线离散，图6是一个离散后的只由直线段构成的字母“O”。

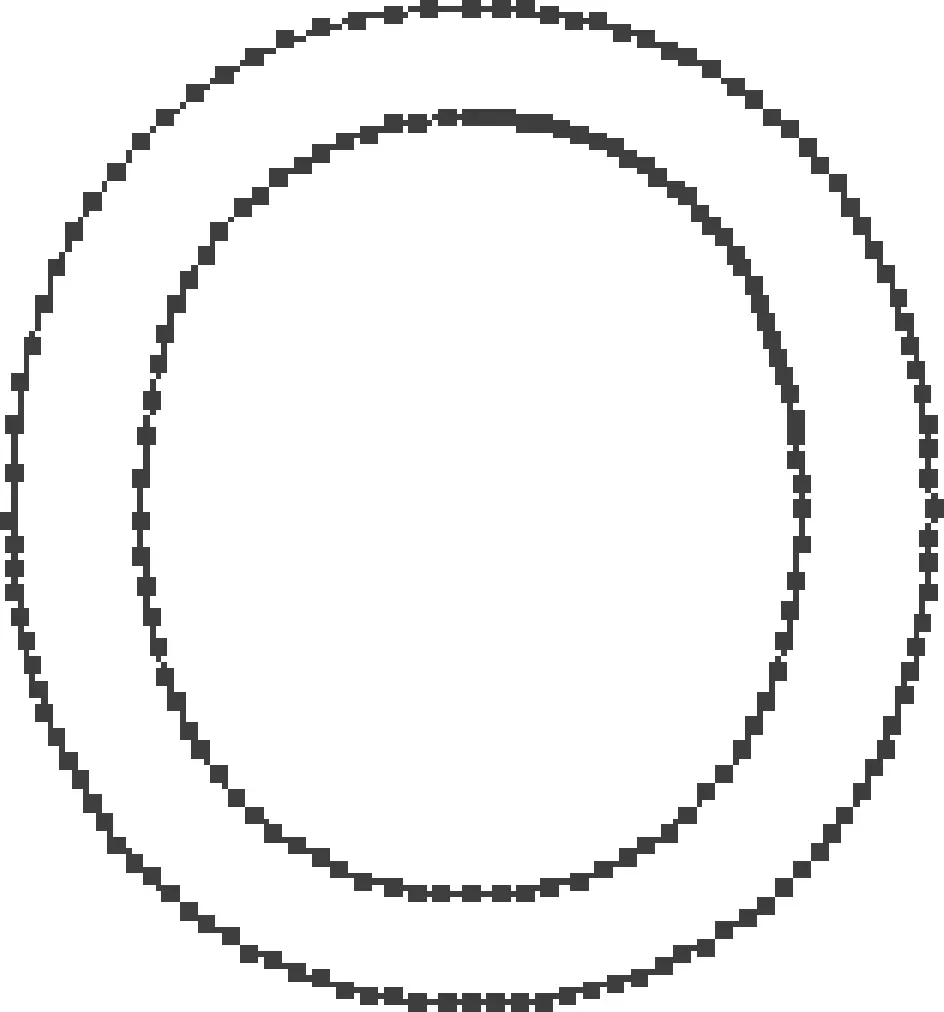
图6 离散后的曲线

通过以上方法得到的图案虽不是原图，但和原图近乎相似，经过数字化处理后投像已被简化成只存在线段的矢量投影。由于线段可以通过两个端点来确定，因此线段的投影又可以简化为点的投影。

2.3 建立方程

图7 空间内模型示意

已知空间内平面公式(法向式)：

xcosα+ycosβ+zcosγ=p

(6)

空间内的直线公式(两点式)：

(7)

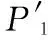
(8)

(9)

(10)

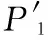
(11)

(12)

z=0

(13)

2.4 全局坐标转化

(14)

对于三维空间内任意两个共原点的坐标系间的转化，都可以通过3个欧拉角的旋转来实现。欧拉角的使用顺序科学界未达成共识，本文作者以zxz顺规的欧拉角为例：参考图8，设定XYZ轴为目标轴，xyz轴为待转轴，xy平面与XY平面的共交线用N表示，α是x轴与N的夹角，β是z轴与Z轴的夹角，γ是N与X轴的夹角。xyz轴到XYZ轴的转化顺序为：先绕z轴旋转α，再绕x轴旋转β，最后再绕z轴旋转γ。最终的转化公式为

(15)

2.5 建立CATIA数据

在CATIA的part数据中按实物尺寸建立数据(见图9)。灯具安装在车辆的正前方，高度200 mm处，灯向下倾斜角度10°。灯具中包含有5×5的透镜阵列，透镜彼此间距4 mm，透镜阵列与原像平面(灯片)平行，距离为8 mm，原像面大小为32 mm×27 mm，投像草图已经过曲线离散化大小为1 375 mm×261 mm，草图距离车辆682 mm。

图8 欧拉角

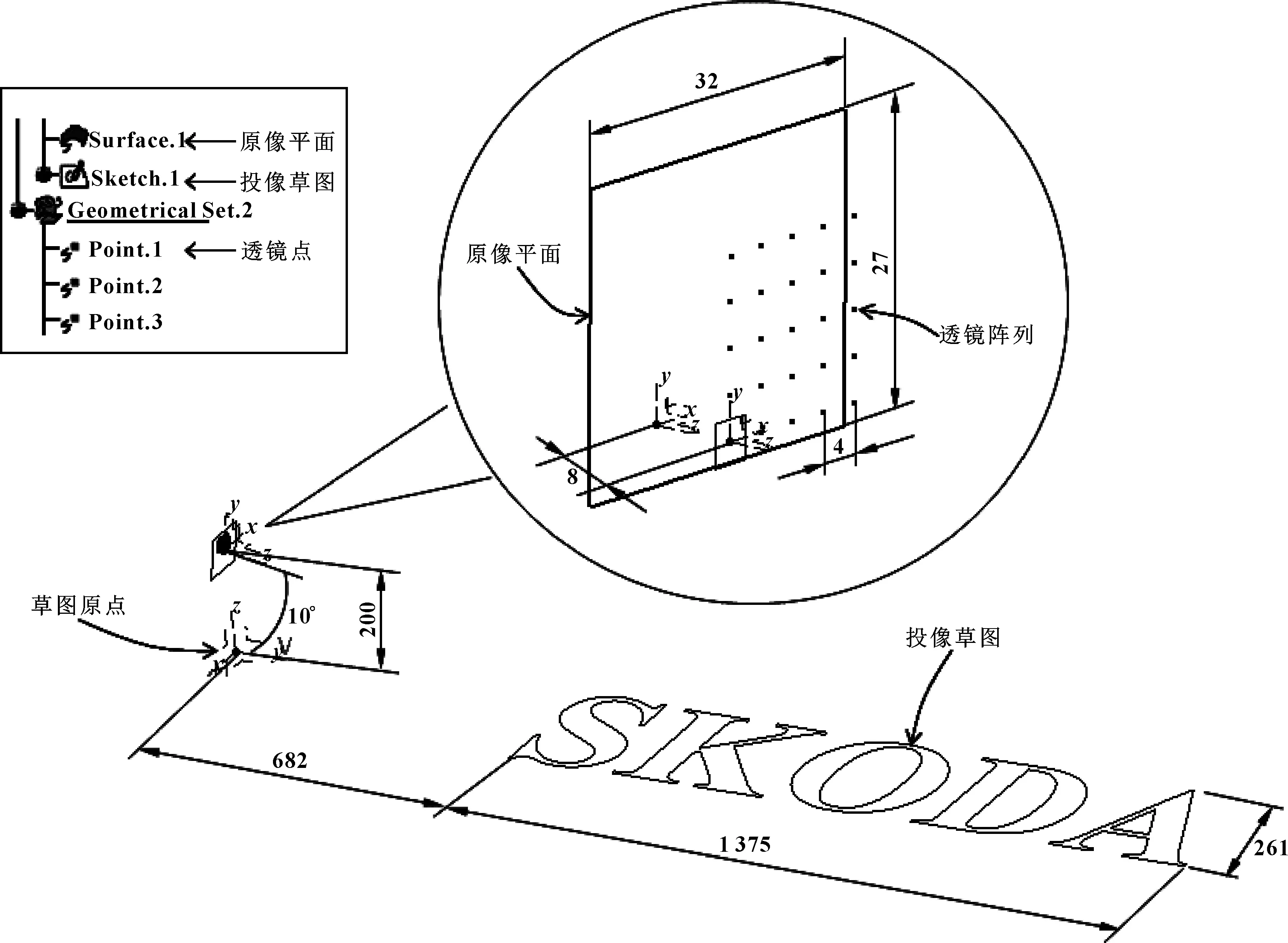
图9 CATIA数据模型

3 程序说明

3.1 程序界面

使用Visual Basic 6.0来编程，图10展示了程序的主界面，其中包含6个部分：

(1)透镜位置。显示当前所选择的透镜点。

(2)灯片位置。显示当前所选择的原像面。

(3)地面草图。显示当前所选的投像草图。

(4)批量作图。勾选时同一几何图形集下所有透镜点会进行批量计算，未勾选时只计算当前所选的透镜点。

(5)开始。点击后开始计算原像。

(6)选择。当选择区各参数都为未选择时显示为“选择”按钮，点击后开始参数选择功能；当选择区已有参数时显示为“清空”按钮，点击后将参数清空。

图10 程序主界面

3.2 程序流程

首先点击选择按钮并进入CATIA依次选择目录树中对应参数(见图9左上方)，当选择区参数选择完毕后，点击“开始按钮”开始计算。通过前一章节的推导得知计算原像时，须求得投像点及透镜点的全局坐标。而投像点和透镜点的全局坐标又通过其局部坐标转化而来，按照这一过程程序的具体计算步骤如下：

(1)首先遍历投像草图内所有线段，并记录每个线段起点和终点的2D坐标。

(2)以投像草图零点为原点，草图水平轴为x轴、垂直轴为y轴建立局部坐标系A2，步骤(1)中记录的2D坐标加上z=0即为投像点的局部坐标。

(3)在原像平面内任取一点为原点，以原像平面为xy平面建立全局坐标系A0。

(4)连接坐标系A2、A0的原点形成直线L1，测量L1长度d1，测量L1与坐标系A0的3个轴的夹角ω1、ω2、ω3，以此求得A2到A0的平移矩阵为(d1·cosω1,d1·cosω2,d1·cosω3,1)T。

(5)将坐标系A2的xy平面和坐标系A0的xy平面相交得直线N。

(6)测量zxz顺规的3个欧拉角，即坐标系A2的x轴与N的夹角α，A2的z轴与A0的z轴夹角β，A0的x轴与N的夹角γ，由此求出3个旋转矩阵依次是：Rz=Rz(α)，Rx=Rx(β)，Rz=Rz(γ)。

(7)将步骤(2)中的投像全局坐标、步骤(4)中的平移矩阵、步骤(6)中的3个旋转矩阵代入公式(15)求出投像点的全局坐标。

(8)以当前透镜点为原点建立局部坐标系A1，则透镜点局部坐标为(0，0，0)。

(9)连接坐标系A1、A0原点形成直线L2，测量L2长度d2，测量L2与坐标系A0的3个轴的夹角δ1、δ2、δ3，以此求得A1到A0的平移矩阵为(d2·cosδ1,d2·cosδ2,d2·cosδ3,1)T。

(10)将步骤(8)中的透镜点局部坐标和步骤(9)中的平移矩阵代入公式(14)求出透镜点的全局坐标。

(11)将步骤(7)中的投像点全局坐标和步骤(10)中的透镜点全局坐标代入公式(11)(12)(13)求出原像点的全局坐标。

(12)根据步骤(11)中的原像点全局坐标在原像平面内作出原像草图。

(13)若批量作图按钮被选中则重复以上步骤(8)—(12)。

(14)新建零件几何体，以原像面做0.5 mm厚的厚曲面，用步骤(12)中做出的草图在厚曲面上开凹槽，得到完整的灯片数据。至此程序运算完毕。

4 结果和评价

对5×5的透镜点进行批量运算，得到原像灯片结果如图11所示。相较于投像，原像是一个倒立的畸变图案，这正是对原像图形进行修正的过程，因为只有这样才能得到一个规整的投像图案。在运算时间方面总计花费时间29 min 30 s。其中步骤(1)—(11)耗时50 s，步骤(12)—(14)耗时28 min 40 s。过程中总计处理了287 000个线段，CATIA花费了大量时间在作草图线段这一步骤上(步骤12)。在处理大批量图形数据时CATIA的运算效率不高，因此导致了此步骤运算时间较长，但CATIA的好处是可以直接生成设计所需的3D数据，此实例中最终的输出物是灯片的实体数据。