变量随机性的游程检验与SPSS实现

杨吉会

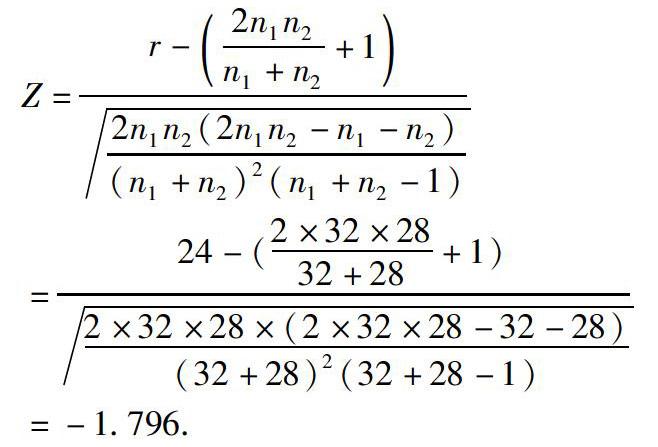
【摘要】非参数检验是数据统计分析方法的重要组成部分，它与参数检验方法共同构成了统计推断理论的核心内容.游程检验是一种常用的非参数检验方法，在众多数据统计问题中都有应用，恰当的理解和运用该数据分析方法，以及掌握其在数据统计软件中的实现过程，对课堂教学和科研工作都具有现实意义.本文结合SPSS软件的使用，阐述游程检验在数据分析过程中的使用方法，并通过具体实例说明该非参数检验方法的有效性和可行性.

【关键词】随机性;非参数检验;游程;SPSS软件

【基金项目】国家自然科学基金（41401322）.

一、单样本的游程检验

非参数检验是数理统计学的一个重要研究内容，是相对参数检验提出的概念.参数检验是在已知总体分布的环境下，对总体分布参数进行推断的方法.非参数检验是在对总体分布的具体形式未知或不是充分了解的情况下，从样本的数据获得需要的信息，对总体分布的类型或总体的其他统计特性进行检验的方法.根据样本数据的来源，主要包括有单样本的非参数检验，多独立样本的非参数检验、多配对样本的非参数检验等[1].针对不同类型的问题提出了不同的非参数检验方法，其中游程检验是一类经常使用的非参数检验方法，其理论的出发点是检验样本的独立性，即检验数据的出现顺序是否是随机的[3-5].这一点非常重要，因为，许多遇到的实际问题中并不只是使研究者关心分布的位置或者形状，也包括样本的随机性，绝大部分经典统计方法在理论上都要求样本具有随机样本，即要求重复观察到的一组变量值在统计上具有独立性，如果样本不是从总体中随机抽取的，则所做的任何推断都将没有价值.游程检验是最简单的判断样本取值顺序是否具有随机性的非参数检验方法.本文通过SPSS软件的使用，通过实例说明这种非参数检验的使用过程.

所谓游程是样本序列中连续出现的变量值的次数r，特别地，在一个0/1序列中，一个由0或1连续构成的串称为一个游程，一个游程中数据的个数称为游程的长度.

一个样本序列的游程个数用r表示.例如，我们投掷一枚硬币，独立重复的进行25次投掷，得到如下的0/1序列：

0000000111111000011110000

上述序列中有3个0游程，长度分别为7、4、4，2个1游程，长度分别为6和4，序列的游程数r=5.显然，该序列0的总个数为n1=15，1的总个数为n2=10，总的试验次数n=n1+n2=25.

一般的，若一个样本序列具有随机性，则这个样本序列的游程数不能太多，也不能太少.当样本序列的长度n1和n2已知时，样本序列的游程数r近似服从正态分布，且有

下面通过具体例子说明利用SPSS软件对单个样本变量取值的随机性进行游程检验的过程.

例1 为检验某耐压设备在某段时间内工作是否持续正常，测试并记录下该时间段内各个时间点上的设备耐电压值的数据如下表：

现利用游程检验法对这批数据进行分析，判断该设备工作是否正常.

解 如果耐压数据的变动是随机的，可认为该设备工作一直正常，否则认为该设备有不能正常工作的现象.因此，检验的原假设H0为该设备的耐压值是随机的，即该设备工作基本是正常的，备择假设H1为该设备的耐压值不具有随机性，即该设备有不能正常工作的现象.不妨取数据的中位数204.55为检验值，小于检验值的数据为第1组，大于等于檢验值的数据为第2组，由此形成由1与2构成的数据序列为

12122121111212122221

容易计算出该序列的游程数r=13，且第1组和第2组各有10个数据，即n1=n2=10，这是一个小样本问题，则有

应用SPSS 23.0软件求解过程如下：

（1）选择菜单【分析（A）】→【非参数检验（N）】→【旧对话框（L）】→【游程（R）】.

（2）选择待检验变量到【检验变量列表（T）】框中.〖HJ1.14mm〗

（3）【割点】框中选择中位数作为分界值.

求解过程如下图所示：

a.中位数

由以上结果可知，中位数204.55，共有20个观测样本.小于检验值与大于检验值的数目各为10，游程数为13，检验统计量的值为0.689，对应的概率P-值为0.491.若显著性水平为0.05，由概率P-值大于显著性水平，故应接受原假设，可以认为该设备在这段时间内工作是基本正常的.

二、两独立样本的游程检验

单样本的游程检验是用来检验单个变量的变量取值是否具有随机性，两独立样本的游程检验则是用来检验两独立样本来自的两个总体的分布是否存在显著差异，这里以瓦尔德-沃尔福威茨游程检验为例进行讨论，检验的原假设H0为两独立样本来自的两总体的分布没有显著差异，备择假设H1为两独立样本来自的两总体的分布存在显著差异.检验方法如下：

首先将来自两总体的两样本按照变量值的升序排列，从而确定出组标记值的一个排列，针对该组标记值的这个排列按照单样本游程检验的方法计算其游程数，如果两总体的分布存在较大差异，则游程数会相对较小;如果游程数比较大，则表明两总体的分布没有明显差异，最后利用公式（1）-（4）计算正态统计量Z获得检验结论[6-8].

例2 在我国的工业和商业企业中随机抽取22家企业进行资产负债率行业差异分析，抽样获得的两类企业某年底资产负债率（% ）数据如下表：

试用两独立样本的游程检验方法判断工业企业与商业企业的资产负债率是否存在显著差异.

解 原假设H0为两类企业的资产负债率没有显著差异，备择假设H1为两类企业的资产负债率存在显著差异.将两类企业资产负债率数据由SPSS数据编辑器窗口录入，工业企业的数据标记为第1组，商业企业的数据标记为第2组，通过SPSS【数据（D）】按钮的【个案排序（O）】功能将资产负债率按照升序排列，由此形成由1与2组标记构成的数据序列为

1111121111222111222222

容易计算出该序列的游程数r=6，且第1组有12个数据，第2组有10个数据，即n1=12，n2=10，这是一个小样本问题，则有

应用SPSS软件求解过程如下：

（1）选择菜单【分析（A）】→【非参数检验（N）】→【旧对话框（L）】→【两个独立样本（2）】.

（2）选择待检验变量到【检验变量列表（T）】框中.

（3）指定存放组标记值的变量到【分组变量（G）】框中，并点击【定义范围（D）】按钮给出组标记值的取值范围.

（4）在【检验类型】框中选择【瓦尔德-沃尔福威茨游程（W）】检验方法.

求解过程如下图所示：

SPSS运行结果如下：

由以上结果可知，共有22个观测样本.工业企业的个案数为12，商业企业的个案数为10，游程数为6，检验统计量的值为-2.384，对应的概率P-值为0.008.若显著性水平为0.05，由概率P-值远小于显著性水平，故应拒绝原假设，接受备择假设，可以认为两类企业的资产负债率存在显著差异.

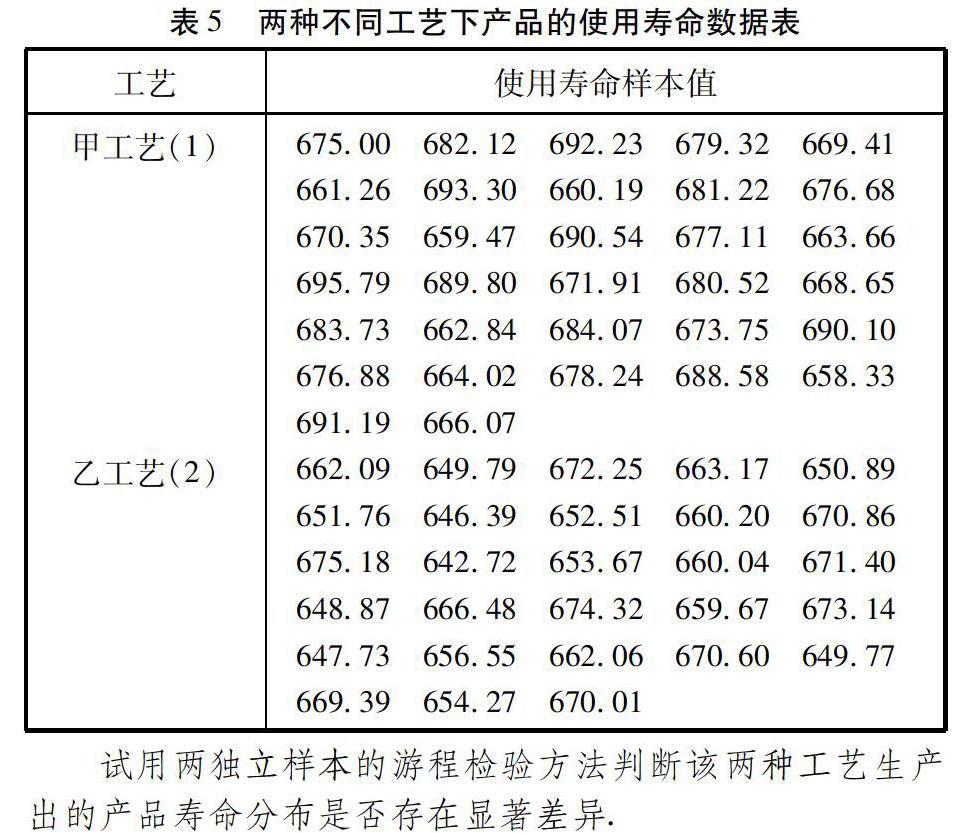
例3 某工厂用甲、乙两种不同的工艺生产同一种产品，现从两种工艺生产出的产品中随机抽取60个产品，获得各自的使用寿命数据如下表：

试用两独立样本的游程检验方法判断该两种工艺生产出的产品寿命分布是否存在显著差异.

解 原假设H0为两种工艺生产出的产品寿命分布没有显著差异，备择假设H1为两种工艺生产出的产品寿命分布存在显著差异.将两种工艺生产出的产品寿命数据由SPSS数据编辑器窗口录入，甲種工艺的数据标记为第1组，乙种工艺的数据标记为第2组，通过SPSS【数据（D）】按钮的【个案排序（O）】功能将产品寿命数据按照升序排列，由此形成由1与2组标记构成的数据序列为

222222222222112212122121112121212221221212

111111111111111111

容易计算出该序列的游程数r=24，且第1组有32个数据，第2组有28个数据，即n1=32，n2=28，这是一个大样本问题，则有

应用SPSS软件求解过程如下：

（1）选择菜单【分析（A）】→【非参数检验（N）】→【旧对话框（L）】→【两个独立样本（2）】.

（2）选择待检验变量到【检验变量列表（T）】框中.

（3）指定存放组标记值的变量到【分组变量（G）】框中，并点击【定义范围（D）】按钮给出组标记值的取值范围.

（4）在【检验类型】框中选择【瓦尔德-沃尔福威茨游程（W）】检验方法.

求解过程如下图所示：

SPSS运行结果如下：

由以上结果可知，共有60个观测样本.甲种工艺的个案数为32，乙种工艺的个案数为28，游程数为24，检验统计量的值为-1.796，对应的概率P-值为0.036.若显著性水平为0.05，由概率P-值小于显著性水平，故应拒绝原假设，接受备择假设，可以认为两种工艺生产出的产品寿命分布存在显著差异.

【参考文献】

[1]王星.非参数统计[M].北京：清华大学出版社，2009.

[2]薛薇.基于SPSS的数据分析（第四版）[M].北京：中国人民大学出版社，2017.

[3]孙建伟，许汴利，苏佳，黄学勇.游程检验及其在流行病学中的应用与探讨[J].预防医学论坛，2017（2）：26-29，32.

[4]李学，刘建民，靳云汇.中国证券市场有效性的游程检验[J].统计研究，2001（12）：43-46.

[5]王静茹，赵以立.游程检验应用[J].中国统计，1993（6）：44-45.

[6]朱凯李悦.RPT方法在多元游程检验中的应用[J].中国卫生统计，2016（2）：362-363.

[7]兰嘉庆，余宛泠.异方差的游程检验[J].中山大学学报（自然科学版），2004，43（z1）：9-11.

[8]Alhakim，A，Hooper，W.A non-parametric test for several independent samples[J].Journal of Nonparametric Statistics，2008（20）：253-261.