变式教学在数学概念课中的应用

吕娜 叶锦锦

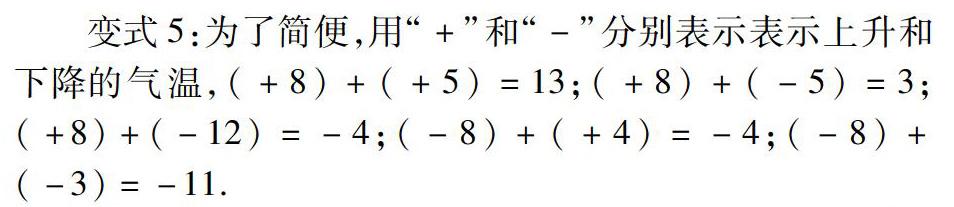
【摘要】变式教学即在教学过程中采用多角度多层次的形式变异，说明知识内容的本质属性.数学课堂中教师运用变式教学，能启发学生对概念、定理、习题、思想方法等的深刻理解和灵活运用.文章从概念课中的“概念形成”“概念理解”“概念应用”角度出发，思考概念变式在概念课教学中的应用.笔者结合教学实例从概念的引入﹑概念的辨析和概念的应用三个方面介绍了变式教学在数学概念课中的应用，引导学生对概念本质的探究，培养提升学生的思维品质.

【关键词】变式教学;概念课;概念变式

学校数学课堂的成功经验之一就是在教学过程中往往会用到变式教学，不同教师不同教法，但大都会有运用变式教学的经历.其优点在于能促进学生对数学概念、定理、方法以及原理的理解和深度学习.笔者在教学过程中发现，学生在学习概念课的时候，常常對概念的前因后果模糊不清，理解认知停留在表面，缺乏应用的灵活性.为了改变这种现状，在教授概念课时笔者常常结合变式教学的方式来开展有效教学，注重概念的强化理解.因此，笔者从概念变式在概念课中的不同形式与应用举例说明，通过由浅入深的变式教学可以引导学生逐步深刻理解并灵活应用概念.

概念变式主要是在形成概念和深化概念的同时引入合理的变异，使得学生在学习过程中从不同方面理解概念，从而深刻掌握概念.其中可以在概念的形成过程、概念的理解过程以及概念的应用过程中引入变式教学，本文结合实例从引入变式﹑辨析变式和应用变式这三个方面分析变式教学在数学概念课中的应用.

一、概念形成过程中的引入变式

数学中的概念往往十分抽象，为此，概念的引入需要建立在学生以往的直观感受和生活经验之上，这样就有利于建立抽象概念与直观感受之间的相关性.由概念的本质特征可将其引入方式分为两类：一是通过现实生活中的形式各样的直观素材或具体实例引入，二是通过数学中抽象的规律、数式或图形引入.

变式运用1 有理数负数和加法法则学习，可以借助实际生活中的气温变化来引入变式.

例：一月份某地周一的最高气温是8℃，周二最高气温比周一最高气温升高了5℃，问周二最高气温是多少？

变式1：一月份某地周一的最高气温是8℃，周二最高气温比周一最高气温下降了5℃，问周二最高气温是多少？

变式2：一月份某地周一的最高气温是8℃，周二最高气温比周一最高气温下降了12℃，问周二最高气温是多少？

变式3：一月份某地周一的最高气温是零下8℃，周二最高气温比周一最高气温升高了4℃，问周二最高气温是多少？

变式4：一月份某地周一的最高气温是零下8℃，周二最高气温比周一最高气温下降了3℃，问周二最高气温是多少？.

变式5：为了简便，用“+”和“-”分别表示表示上升和下降的气温，（+8）+（+5）=13;（+8）+（-5）=3;（+8）+（-12）=-4;（-8）+（+4）=-4;（-8）+（-3）=-11.

变式6：上面题目中气温上升和气温下降表示了一对相反意义的量，用“+”和“-”表示，生活中还有很多这样的量，请同学设计具有相反意义的量的加法的例子.

设计小结：从具有相反意义的上升和下降的气温引入正数和负数，让学生认识到引入负数对实际生活有重要的意义，从而了解数的扩充，为有理数的概念打下基础.对有理数加法的概念，很多学生由于对加法的意义理解不透彻导致后面难以理解法则，运算不过关.设计以上变式题目，结合实际生活经验，学生容易理解加法中“正数+正数”“正数+负数（负数+正数）”“负数+负数”的实际意义.

变式运用2 在整式的学习中，单项式的概念可以通过具体数和代数式进行引入变式，引导学生逐步归纳出单项式概念.

题目：观察下列式子有什么特点？

0，100，32，-2 5，0.5，a，y.

变式1：观察下列式子有什么特点？

100x，32y，-2m 5，0.5xy，-a.

设计小结：在教学中引导学生观察式子的特点，从“单独一个数字或者一个字母组成的式子”和“数字与字母的乘积组成的式子”两个角度，发现这些式子是由“单独一个数字或者字母以及数字与字母的乘积组成的”，为引入单项式的概念做铺垫.

二、概念理解过程中的辨析变式

引入概念后，为了进一步挖掘其内涵和外延，需要设计辨析变式加深理解.因此，我们可以从概念的内涵——即本质属性和外延——即包含的事物范围两方面来进行辨析变式的教学设计.

变式运用3 在讲授一元一次方程这个概念时，学生常常不能全面的把握未知数、次数、整式等关键概念，为了帮助学生形成正确深刻的理解，可以针对这一概念的内涵、外延，设计如下变式训练：

说出哪些式子是一元一次方程：

① x=0;② x+2（x-1）=0;③ a 2-3=0;④ 3y=2x+1 2;⑤ xy=0;⑥ x2-2x+2=0;⑦ 2x+1>0;⑧ 5x-1 x=3;⑨ 1 x=1.

设计小结：①②③是从学生容易错的概念的内涵设计的辨析变式，使学生掌握符合概念的三个条件，④⑤是从“一个未知数”来设计的变式反例，⑤⑥是从“次数是1”来设计的变式反例，⑦⑧⑨是从“等号两边都是整式”设计的变式反例;通过以上辨析变式，有关一元一次方程的概念在学生脑海中已经清晰.

三、概念应用过程中的应用变式

学生理解了概念后，通过设计由浅入深的应用变式巩固概念，并对同一类型的题目进行总结和拓展提升，触类旁通，充分锻炼了学生思维的深度和广度.

变式运用4 为了让学生更好地理解算术平方根的双非负性，设计如下应用变式.

题目：已知x-2+（y+1）2=0，求x+y的值.

变式1：已知x-y+|y+2|=0，求yx的值.

变式2：已知|x-2|+（y+1）2+z-3=0，求（y-3z）x的值.

变式3：已知|1012-x|+x-1013=x，求x-10122的值.

变式4：已知y=2x-1-1-2x+6x，求6x+y-2的值.

变式5：已知x，y满足x2=1+y-2 2-2-y 3，且|x|+x>0，求2018 xy+2018 （x+1）（y+1）+2018 （x+2）（y+2）+…+ 2018 （x+2016）（y+2016）的值.

设计小结：变式1和变式2把绝对值﹑平方和算术平方根的非负性串联在一起，可以快速地联系起已学过的几种具有非负性特征的概念;变式3把被开方数的非负性和绝对值串联起来，进一步提升了运用所学知识进行变通拓展的能力，同时强化概念核心.变式4和变式5要求学生理解被开方数的非负性，并能用裂项法求和，提升了学生的思维能力.

如今，课堂改革突出以学生为主体，在以生为本的教与学中实现培养学生形成数学核心素养的目标.变式教学在概念中的应用需要教师精心设计变式的问题和题目，引导学生从“变”中探究“不变”的本质和规律，拓展学生的思路，将数学的知识、方法和思想融会贯通，以达到深入理解和灵活运用，指导学生学会深度学习，提升学生的综合能力.

【参考文献】

[1]刘长春，张文娣.中学数学变式教学与能力培养[M].济南：山东教育出版社，2001：11-27.

[2]沈兰，郑润洲.变革的见证顾泠沅与青浦教学实验30年[M].上海：上海教育出版社，2008：141.

[3]孙霞.运用“概念性变式”促进本质建构——以“一元一次方程”的教学为例[J].中学数学教学参考，2017（6）：28-30.