巧用数形结合思想

高文龙

【摘要】许多面临高考的学生，都会由于数学思想的抽象性而对这门学科产生望而生畏的心态，十分不利于其在考场上的高水平发挥.而在实际的教学过程之中，许多教师都会将数形结合作为一种化解数学抽象性难题，提高其直观度的有效手段，并以此来帮助学生不断提高解答数学客观题的能力.这一数形结合思想在解决函数等问题的时候效果尤其显著.因此，以这一思想在高考数学客观题解答过程中的應用为出发点进行深刻探究，以期为高中生数学解题能力的提升贡献一分力量.

【关键词】数形结合思想;高考数学;客观题;三角函数;画图

数形结合思想的本质，是借助于图像这一直观的方式，来对抽象性较强的数学知识进行直观化的转变[1].尤其是在高考数学的客观题当中，有许多题干知识所给出的信息都较为抽象，不符合人脑的思考特征，需要借助图像对其进行从抽象到具象的转化，才能够帮助学生更好地在复杂的信息中寻求最优化的解决策略.

本文以这一有效方法在高考客观题解答过程中的应用展开生动的案例分析.

一、浅析数形结合思想在解答高考数学客观题当中的作用

只要对历年的高考数学真题进行分析，我们就能够发现，其各类题型都在不同程度上渗透着数形结合的思想[1].而这类题目就其出题意图来看，往往旨在于对学生的空间想象力以及逻辑推理等能力进行深入的考查，以此来评估学生的综合数学水平.因此，解决此类问题最佳的途径，就是通过画图这一形式，将抽象的数学信息转化为可直观感受的图形，并在数字与图案的交互过程中，进一步激发学生解题灵感的出现，提高其在考场上的综合应变水平.但是在这一数形结合思想的应用过程当中，也有许多因素的重要性不容忽视，那就是图像的规范性及其特殊辅助线、辅助点的选取是否有效等内容.只有对以上内容进行有效把控，最终才能突破数形结合思想应用的局限，使其真正在高考考场上发挥应有的价值.以下通过具体的案例分析，来探究这一数形结合思想的应用方式[1].

二、数形结合思想在高考数学客观题解题过程当中的应用案例

（一）在解答函数图形问题当中的应用

函数图形问题是历年高考数学的必出题目，而一般来说，如果仅仅通过题干的信息及对数学公式的运算，我们很难将抽象知识转化为容易理解的直观形象，从而轻松地找到题目的正确解.而若能够在这一过程中恰当地引入数形结合的解题技巧，就能够使考生应对这一类题目的能力获得不容小觑的提升[1].

案例1 已知条件：f（x）=|x-2|+1，与此同时g（x）=ax.如果f（x）=g（x）这一方程式能够解出两个数值不相等的实根，那么此时实数a该如何取值？

图1

解答过程如下：根据上述已知信息，我们可以作出如图1所示的图形.接下来，再根据图像当中显示的这两大函数的斜率，来推断其实根的范围是：小于1且大于12的实数.

（二）在解答方程根数问题过程中的应用

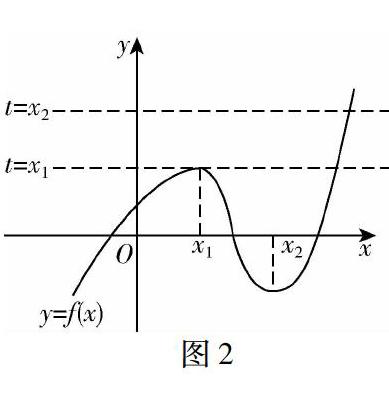
案例2 函数f（x）的方程式为f（x）=x3+ax2+bx+c的前提下，已知这一函数有两个极值点，分别是x1和x2.与此同时，还知道f（x1）的值就等于x1本身，且x2大于x1.此时，要求3（f（x））2+2af（x）+b=0这一方程所拥有的实根的个数.

图2

解答过程如下：根据方程的已知条件，我们可以作出如图2所示的图形.接下来，再借助令t等于f（x）这一操作，来将上述第二个方程转化为参数更为简单的3t2+2at+b=0这一方程.接下来，再根据这一方程的信息，推演出t分别等于x1和x2这一结果.最终根据图像当中的交点及相关的已知信息，判断其最终的实根数量为三个[2].

（三）在含参数不等式当中的应用

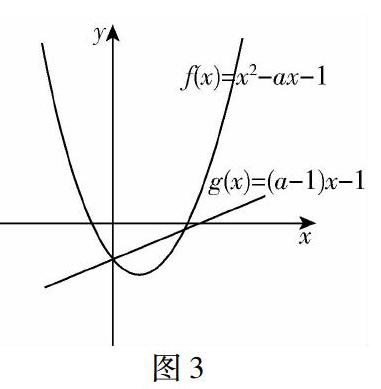
案例3 在a属于实数集R的前提下，如果当x大于零的时候，不等式[（a-1）x-1]（x2-ax-1）≥0一直成立，那么此时a的值为多少？

图3

解答过程如下：根据上述的已知条件，我们可以将不等式拆分为两个函数，一个是f（x）=x2-ax-1，另一个是f（x）=（a-1）x-1.然后在此基础上作出如图3所示的函数图，画出两个函数的交叉图像.从图像的内容我们可以得知诸多信息.首先，两个函数都必然经过同一个点，这个点的坐标为（0，-1）.其次，为了满足题干当中提出的前提条件，这两大函数的另一个交点位置，必然处于x轴之上[3].此时，将y=0代入到y=（a-1）x-1这一方程当中，我们就可以得知这一交点坐标的表现形式，为1a-1，0，此时其中的a值大于1.再将这一坐标的数值代入到上述的另一个方程中，我们就可以得出a=32.

三、结束语

根据上述的讨论，我们可以得知，在高中数学当中解答不同类型的客观题的时候，都会在不同程度上需要应用到这一精妙的数形结合思想.这一思想的普及为高中生破解抽象性较强的数学题提供了一条光明大道，使其能够在不断加深对这一思想的应用水平的过程中，逐步提高其解答数学题的效率[3].

【参考文献】

[1]陈俊斌.巧用数形结合思想，妙解高考数学客观题[J].数学教学，2015（10）：43-46.

[2]廖雷，王涛.巧用数形结合思想提升中学生的解题能力[J].农家参谋，2018（17）：183.

[3]陈德前.数形结合妙解生辉——谈数形结合思想在解题中的应用[J].中学生数理化，2016（7）：14-16.