残差自回归模型在甲型病毒性肝炎发病数预测中的应用
2020-06-01刘天姚梦雷黄继贵夏世国陈红缨黄淑琼吴杨陈琦刘漫
刘天, 姚梦雷, 黄继贵, 夏世国, 陈红缨, 黄淑琼, 吴杨, 陈琦, 刘漫
甲型病毒性肝炎(简称“甲肝”)是由甲型肝炎病毒(hepatitis A virus,HAV)引起的以肝脏病变为主的急性传染病[1]。甲肝主要经粪口感染,由于不洁饮食、饮水史常可造成大规模流行。近几十年来,甲肝暴发疫情仍有报道,甲肝仍然是我国重要的公共卫生问题,防控形势十分严峻[2-3]。利用数学模型拟合历史数据并准确预测其发展趋势,对于甲肝防控策略和措施的制定具有至关重要的作用。残差自回归模型具有精度高、易于理解的特点,近年来被国内学者应用于手足口病、艾滋病等疾病的预测,效果较好[4-5]。但目前残差自回归模型应用于甲肝预测预警的研究尚未见报道。为此本文拟采用残差自回归模型拟合2001—2013年某省甲肝发病数据,并进行外推预测,以探讨该模型在甲肝发病数预测中应用的可行性,为甲肝的精准防控提供科学依据。
1 资料与方法
1.1 资料来源
数据来源于2001—2014年某省“公共卫生科学数据中心”平台的甲肝逐月发病数,2001—2014年该省甲肝逐月发病数即为一组时间序列数据。
1.2 模型原理
残差自回归模型的基本思想是基于因素分解法,提取出原始序列中主要的确定性信息后对残差序列建立自回归模型,以充分利用时间序列中的确定性信息和随机性信息[6]。
1.2.1 因素分解根据Cramer分解定理,原始时间序列Xt可以按公式Xt=Tt+St+εt进行分解,其中,Tt为趋势效应拟合;St为季节效应拟合;εt为残差。
1.2.2 趋势效应拟合通常采用两种方式对趋势效应进行拟合,第一种是自变量是时间t的幕函数,即:
Tt=β0+β1t2+β2t2+…βktk+εt
第二种方法是自变量是历史观察值{Xt-1,Xt-2,…Xt-γ}的函数,即:
Tt=β0+β1Xt-1+β2Xt-2+…βγXt-γ
第二种方式和差分方式的原理相同,在实际应用中通常采用第一种方法对趋势效应进行拟合。
1.2.3 季节效应拟合对季节效应的拟合也有两种方式,第一种是使用已知的季节函数,即:
St=St′
其中St′为已知的季节函数;
第二种方法是建立季节自回归模型,设季节性周期为m,其公式如下:
St=α0+α1Xt-m+α2Xt-2m+…αlXt-
lm+εt
本文采用第一种方法进行季节效应拟合。
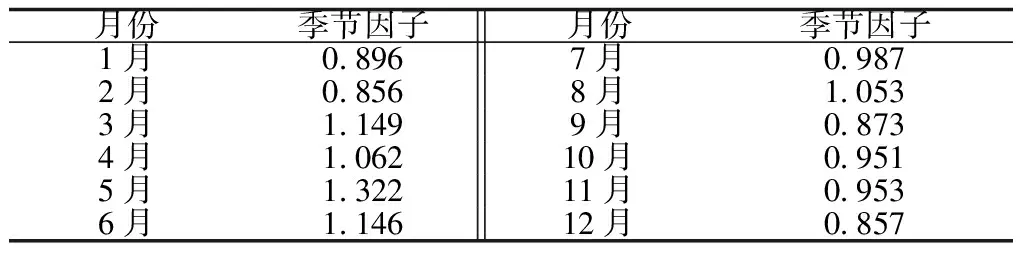
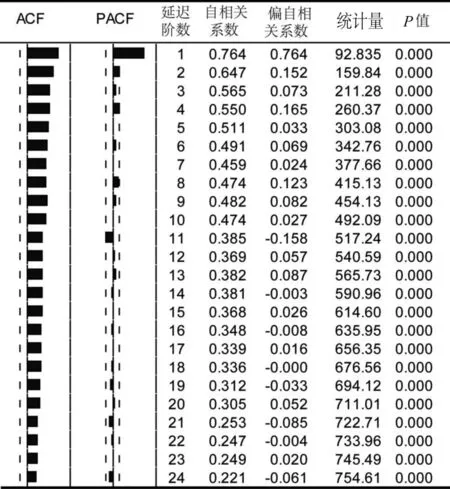
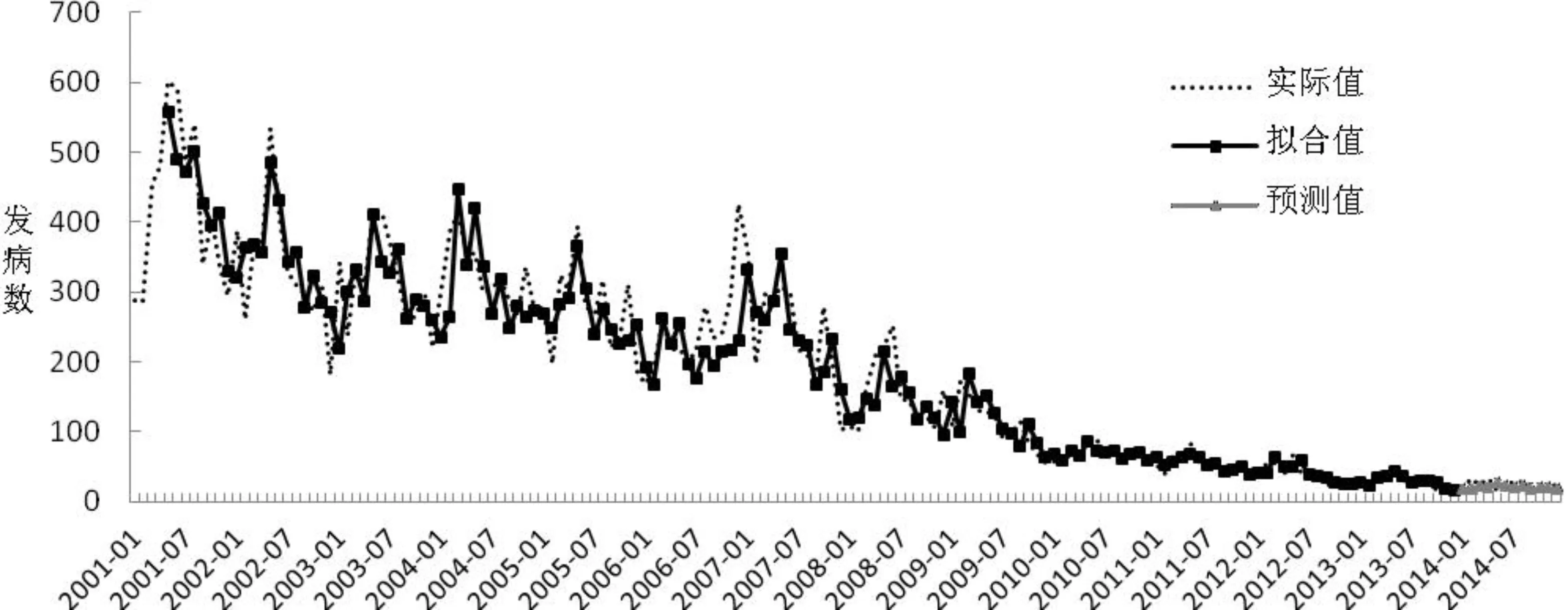
1.2.4 自回归分析考虑到因素分解法对确定性信息的提取可能不够充分,因而需要进一步检验残差序列{εt}的自相关性。自相关检验通常采用Durbin-Waston检验(简称DW检验)检验残差的自相关性,若DM εt=φ1εt-1+φ2εt-2+…φpεt-p+αt 综上,残差自回归模型可以表示为: 以2001—2013年某省甲肝月发病数据拟合残差自回归模型,利用2014年逐月甲肝发病数回代检验模型的预测效果,根据R2、相对误差(RD)、平均绝对误差百分比(MAPE)、平均误差率(MER)、均方误差(MSE)和平均绝对误差(MAE)评价模型拟合、预测效果。运用Excel 2007和Eviews 9.0进行统计分析,检验水准α=0.05。 2001—2014年该省累计报告甲肝31 766例,月平均报告189 083例,甲肝发病整体呈逐年下降趋势。甲肝各月均有病例报告,累计发病无明显季节高峰,3-6月份报告病例数相对较多,占病例总数的39.375%。图1。 采用季节分解法分解出序列中的季节成分,本文采用相乘法分解季节因素,将原始序列{xt}除以季节指数(St),消除季节影响,得到不含季节因素的序列{Xt}。季节指数见表1。 表1 季节分解法分解出的季节指数(St) 通过观察序列{Xt},具有一定的线性变动趋势,尝试对序列{Xt}分别拟合直线回归和取对数后拟合直线回归两种,拟合结果见表2,后者R2大于前者,AIC值小于前者,且参数估计均有意义,确定趋势效应拟合模型为:log(Xt)=6.457-0.019t,其中t为月份序号,如2001年1月为1,2001年2月为2,……,2014年12月为168。见图2。 表2 两种趋势拟合模型的参数估计及拟合优度检验 对上述拟合趋势模型后的残差序列{εt}进行DW检验,DW值为0.536。按自变量个数为1个,样本量n=168查DW界值表,下限1.720 图2 残差序列{εt}的ACF图和PACF图 图3 AR(1,4)模型残差的ACF图和PACF图 最终确定残差自回归模型公式如下: 拟合及预测结果见表3和图4。 表3 残差自回归模型的拟合及预测效果评价 图4 残差自回归模型拟合值、预测值与实际值比较图 我国于2004年建成全球最大的基于互联网的法定报告传染病监测信息报告管理系统,在全国范围内实现了传染病个案的信息化录入和集中保存,为充分处理和分析监测数据创造了条件[7]。自此我国传染病预测、预警技术得到迅猛发展,ARIMA模型作为时间序列预测预警的经典模型已在传染病监测领域得到广泛应用[8];而残差自回归模型被用于传染病预测预警,尤其是甲肝的预测预警并不多见。本文使用某省甲肝逐月发病数拟合残差自回归模型,结果显示,拟合值相对误差为1.863%,预测值相对误差为11.797%,拟合及预测效果均优于王永斌等[4]应用残差自回归模型对我国手足口病发病率进行的拟合及预测。相关报道指出,模型拟合及预测的相对误差均低于20.00%即为合格模型[9],可以认为残差自回归模型用于该省甲肝发病数预测的效果较好,可以用于该省甲肝发病数的短期预测。 残差自回归模型的参数估算方法种类繁多,常用的包括直接最小二乘法、两步法和非线性最小二乘法。武新乾等[10]利用蒙特卡洛模拟计算结果表明,非线性最小二乘法的拟合及预测精度均高于直接最小二乘法和两步法,本文采用非线性最小二乘法进行拟合及预测,精度较高,提示残差自回归模型以非线性最小二乘法效果较好。 目前,ARIMA模型是疾病预测预警应用最为广泛的模型。ARIMA模型利用差分思想建模,但差分很难对模型进行直观解释[6]。而残差自回归模型不存在这个问题,其优点在于结果便于理解,更能准确地解释确定效应的影响。如本文拟合结果表明,该省甲肝发病数无明显季节高峰,但3-6月报告病例数较多;另外该时间序列拥有一个长期的非线性递减趋势,呈自然对数下降变化;同时,它还受到诸多因素的影响,导致随机波动序列具有短期自相关性,经自回归拟合,信息得到充分提取,模型拟合预测精度均较高。而以上信息ARIMA模型往往无法给出合理解释。因此在实际应用中,建议研究者尝试采用多种模型拟合数据,在拟合精度相近的前提下,建议采用残差自回归模型进行拟合,便于从专业角度解释拟合结果。 综上所述,甲肝月发病数拟合残差自回归模型效果较好,可以用于短期预测。残差自回归模型具有结果便于解释、拟合精度高等优点,在疾病最优预测、预警模型探讨中值得深入研究。但残差自回归模型在实际应用中也存在一定局限性。首先,残差自回归模型无法利用软件直接建模,需多步运算;其次,用于分析的时间序列点不易过少,一般不少于30个[11],样本量较短的序列不宜拟合残差自回归模型。1.3 统计分析
2 结果
2.1 疫情基本情况
2.2 季节效应拟合
2.3 趋势效应拟合

2.4 自回归拟合
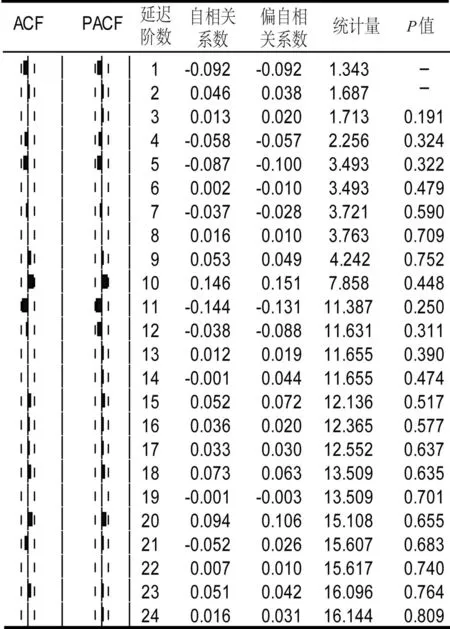
2.5 最终模型
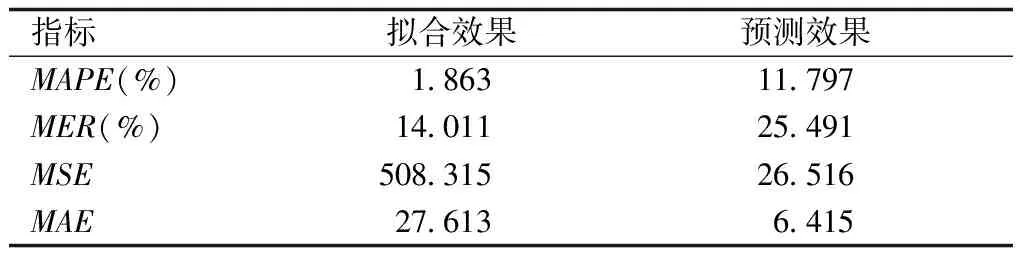
3 讨论
