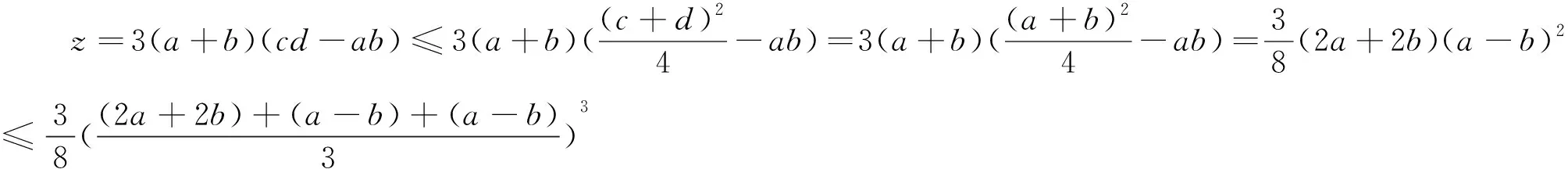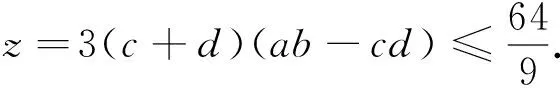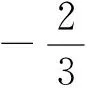一个最值问题的三个简解

四川省成都华西中学 (610051) 戴向阳

本文给出文[1]问题的简解.

题目设实数a,b,c,d∈[-2,2],且a+b+c+d=0,求z=a3+b3+c3+d3的最大值.

解法1:z=(a+b)((a+b)2-3ab)+(c+d)((c+d)2-3cd)=(a+b)3+(c+d)3-3((a+b)ab+(c+d)cd)=-3((a+b)ab-(a+b)cd)=-3(a+b)(ab-cd)=-3(a+b)(ab+c(a+b+c))=-3(a+b)(b+c)(c+a).不妨设a+b=min{a+b,b+c,c+a}.若(a+b)(b+c)(c+a)<0,则a+b,b+c,c+a<0或a+b<0,b+c>0,c+a>0.

当a+b,b+c,c+a<0时,z=3(-(a+b))(-(b+c))·(-(c+a))≤

当a+b+c+d=0,-(a+b)=-(b+c)=

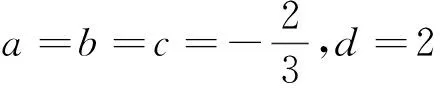
当a+b<0,b+c>0,c+a>0时,z=

3(-(a+b))(b+c)(c+a)≤

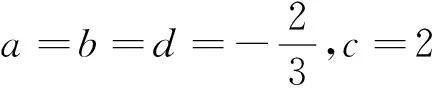
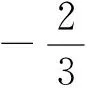
解法2:不妨设a+b≤b+c≤c+a，由解法1知z=-3(a+b)(b+c)(c+a)

≤3|a+b||b+c||c+a|

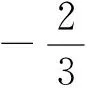
解法3:由解法1知,z=3(a+b)(cd-ab).