谈小学数学计算课练习的有效性设计

庄迎春

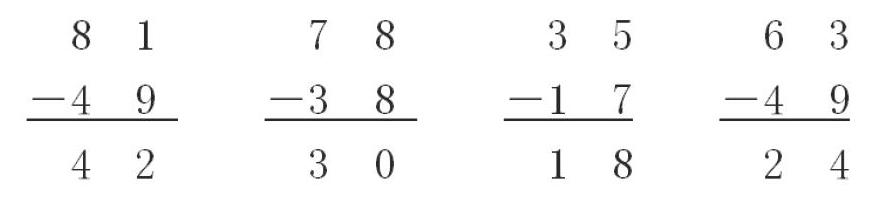
【摘 要】练习是学生在教师指导下独立运用知识、解决问题、发展智能的教学活动，是学生学习过程中的重要实践活动，具有巩固技能、反馈评价、形成策略、解决问题、拓展思维的功能。练习的主要任务是巩固基础知识和形成熟练的技能。心理学认为，一个正确认识的获得，总要经过由实践到认识、由认识到实践的多次反复。反映在教学规律上，学生要获得知识和能力，也要有一个多次反复的过程。计算教学中学生也要进行一定量的练习，否则就不能牢固地掌握计算方法，学生的计算能力也不能很好的形成。

【关键词】小学数学;计算练习;有效性设计

【中图分类号】G623.5  【文献标识码】A  【文章编号】1671-8437（2020）04-0186-02

练习是学生在教师指导下独立运用知识、解决问题、发展智能的教学活动，是学生学习过程中的重要实践活动，具有巩固技能、反馈评价、形成策略、解决问题、拓展思维的功能。可是在平时的计算教学中练习设计存在着以下的问题：①练习设计的层次性不够，各种各样的练习安排了很多，但为什么要这样安排？教师没仔细考虑过。②练习题不够精挑细选，如何打造簡约课堂，如何让一道练习题发挥多重作用？教师没有考虑。③新课前的复习铺垫，选择什么样的复习题，为什么要复习这些内容，没仔细考虑过。很多教师只是为了复习而复习，课堂结构看起来完整实际却不然。为什么会存在这样的问题，原因就在于，教师对本节课要完成的，教学目标定位不准确;或找的练习材料过多，不知道如何整合和精简;或是对小学阶段计算课的知识体系不够明确，不清楚每一年段对计算的具体要求[1]。

在小学阶段学生学会计算方法，提高计算能力，形成计算技巧，都需要学生反复的练习来实现。课堂中，教师练习的设计要有针对性，学生练后才有效果，才能让学生形成良好的计算能力。

在计算教学中我们该如何更好的来设计课堂练习呢？

1   根据教材体系中的地位设计练习

如在三年级上册《三位数加三位数连续进位加法》教学中，小学阶段学生对笔算加法的学习，就到三位数加三位数的连续进位。而在学生学习了亿以内的数后，就没有安排笔算加法的内容了。那学生是不是不用计算四位数加四位数了？这时就要学生利用知识的迁移，把三位数加三位数的笔算方法利用到四位数加四位数，甚至更多位数的加法。因此，在教学三位数加三位数的连续进位加法时，可以这样做：首先要复习两位数加两位数连续进位的笔算方法[2]。如76+84通过这道题的计算，使学生回忆起加法的笔算方法：相同数位对齐，从个位加起，个位满十向十位进一，十位满十向百位进一。复习后让学生尝试计算445+298，反馈展示学生的作业。在作业展示中，让学生充当小教师，由其他学生提出自己的疑问，在学生与学生的互动中，讲清笔算的过程。再在师生互动中理清连续进位的笔算方法。接着教师引导学生观察76+84和445+298这两道题，发现不管是两位数加两位数的笔算还是三位数加三位数的笔算，都是以相同数位对齐，从个位加起，哪一位满十，就向前一位进一。然后分层次让学生进行练习，连续进位可以从个位十位连续进位、十位百位连续进位、个位十位百位连续进位三种情况进行设计。最后可以拓展到四位数加四位数的笔算，如3847+6153，通过让学生算一算感知“哪一位满十就向前一位进一”，概括出多位数加多位数的计算方法。

2   根据知识的难易度设计练习

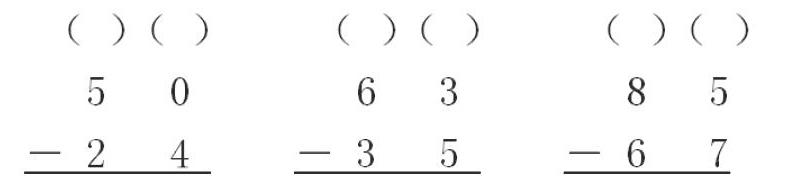
在计算教学中，由于内容不同，学生学习时难易度也不同。对于比较难的内容，教师尽量在授课时讲解得简单一些，而对学生来说比较简单的内容，在教学设计时就要考虑如何把课上得深入一些。如在教学两位数减两位数时，学生很好理解不退位减法，但在学习退位减法时，像这种个位不够减，要从十位退1作10和个位上的数加起来再减的情况，学生还是第一次碰到。因此，在练习的设计中可以设计过渡性的练习题：

让学生填个位实际上是几去减的？十位退一后变成了几再减？

再如：让学生当小教师判断下面的计算对吗？把错误的改正过来。

通过这些练习题来强化十位退一后一定要先减掉1再减。

再如五年级的《小数除以整数》，学生先复习整数除法，算一算224÷4，再学习22.4÷4，从224÷4到22.4÷4学生迁移比较容易。因此，教师要深入挖掘如何设计练习。例题22.4÷4=5.6中，商的整数和小数部分都只有一位，教师在练习设计中就要考虑商的整数、小数部分有两位的练习，商中间有零的这样的练习题。为了使学生练习更有层次性，可以设计以下两组笔算题：①18.2÷14，117.5÷25，249.6÷8，73.5÷6。②284.9÷7，9.18÷9，642.84÷6一组商中间未出现“0”。另一组商中间出现“0”通过这样的对比练习，让学生明确什么时候商中间有0，商中间有0的情况怎么处理。

3   根据课型设计练习

计算课一般分学习新知、练习和复习这三种课型，每一类课型都有自己的教学目标，教师在教学中要根据不同的教学内容和不同的教学目标，设计有针对性的练习题。如学生在学完小数乘小数的笔算后，教师可以通过课后练习，设计帮助学生更快更准确地确定积的小数点的位置，帮助学生更好地掌握小数乘小数的笔算方法。

第一层次：回顾小数乘法的计算法则：计算12.4×0.8，师问如何确定积是几位小数？计算0.56×0.05，师问为什么这道题的积是0.028而不是四位小数？乘得的积的小数位数不够，怎样点小数点？

第二层次：根据206×25=5150，直接写出下列各式的积。你能快速说出下面各题的积是多少吗？20.6×25=（   ），2.06×2.5=（   ），0.206×2.5=（  ）。给因数添上小数点使等式成立206×25=5.15。

第三层次：出示2.4×0.8，2.4×1，2.4×1.8计算并观察，你有什么发现？根据学生回答教师小结，一个数（0除外）乘大于1的数，积比原来的数大。一个数（0除外）乘小于1的数，积比原来的数小。接着让学生在○里填上>或<，0.71×2.8○0.71 12×0.7○12×1.85 0.71×2.8○2.8  3.4×0.5○1.6×3.4，通过练习让学生感知并小结得出刚才发现的规律，可以让我们不计算也能快速比较大小，让学生体会数学的神奇。

4   结语

不管是新授课中的练习，还是练习课或复习课中的练习，教师都必须明确学生掌握了多少新知识，计算技能掌握得如何。只有这样教师才能根据教学目标、教学重难点、以及学生的认知规律合理地选择练习题，使练习更有效率。也只有这样才能使练习既起到巩固知识、训练技能的目的，又能促进学生的思维发展。

【参考文献】

[1]高静娟.小学数学计算能力提升策略[J].甘肃教育，2018（20）.

[2]王芸森.小学生数学计算能力的培养[J].基础教育研究，2018（4）.