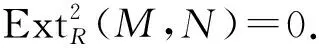(m,n)-纯 遗 传 环

郭景阁, 杨璐璐, 赵仁育

(西北师范大学 数学与统计学院, 兰州 730070)

关于遗传环及各类广义遗传环的研究目前已有很多结果： Geng等[1]研究了内射模的商模都是纯内射模的环----纯遗传环； Hu等[2]研究了每个纯左理想都是投射模的环----PIP-环, 并讨论了PIP-环与F-环及Noether环和完全环的关系； Moradzadeh-Dehkordi等[3]研究了左理想都是FP-投射模的环----FP-遗传环.设m和n是两个任意取定的正整数, 作为FP-内射模的推广, Chen等[4]引入并研究了(m,n)-内射模； Mao等[5]引入了(m,n)-投射模的概念; 杨璐璐等[6]引入并研究了(m,n)-遗传环.受上述工作的启发, 本文引入并研究(m,n)-纯遗传环.

1 预备知识

本文中的环均为有单位元的结合环, 模均是酉模,m,n是两个任意取定的正整数.

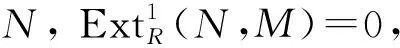
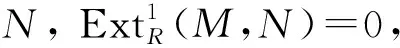
定义3[9]设R是环, 形如Rm/K的左R-模称为(m,n)-表现左R-模, 其中K是左R-模Rm的n-生成子模.

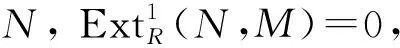
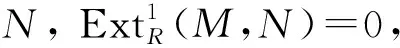
定义6设M是左R-模,M的(m,n)-投射维数(m,n)-pdR(M)定义为

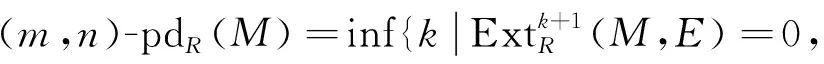
如果满足条件的k不存在, 则规定(m,n)-pdR(M)=∞.

定义7[6]设R是环, 如果R的每个左理想都是(m,n)-投射的, 则称R是左(m,n)-遗传环.

2 主要结果

受PIP-环和(m,n)-遗传环研究的启发, 本文引入(m,n)-纯遗传环的概念.

定义8设R是环, 如果R的每个纯左理想是(m,n)-投射模, 则称R是左(m,n)-纯遗传环.

命题1设R是环.如果:

1)R是左遗传环;

2)R是左(m,n)-遗传环;

3)R是左FP-遗传环;

4)R是左纯遗传环;

5)R是左PIP-环;

6)R是左(m,n)-纯遗传环.

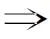
设M是左R-模.由文献[10], 如果对任意左R-模的纯正合序列0→A→B→C→0, 均有

0→HomR(C,M)→HomR(B,M)→HomR(A,M)→0

正合, 则称M是纯内射的.如果R是纯内射左R-模, 则称R是左纯内射环.

命题2设R是左纯内射环, 则下列结论等价:

1)R是半完全环;

2)R是左PIP-环;

3)R是左(m,n)-纯遗传环.

因为R是左(m,n)-纯遗传环, 所以I是(m,n)-投射模.于是由文献[6]中定理1知, 存在左R-同态g:I→R, 使得f=πg.因为R是左纯内射环, 所以存在左R-同态h:R→R, 使得hi=g.故f=πg=(πh)i.表明f可以扩张为R到R/J的同态, 矛盾.因此R是半完全环.

命题3如果环R的每个平坦左理想都是(m,n)-投射的, 则R是左(m,n)-纯遗传环.

证明: 设I是R的纯左理想, 则由文献[13]中推论4.86知,I是平坦左R-模.从而由条件知I是(m,n)-投射模, 因此R是左(m,n)-纯遗传环.证毕.

文献[2]中定理1.1证明了R是PIP环当且仅当每个循环平坦左R-模的投射维数不超过1.对左(m,n)-纯遗传环, 有:

定理1设R是环, 则R是左(m,n)-纯遗传环当且仅当每个循环平坦左R-模的(m,n)-投射维数都不超过1.

证明: 必要性.设I是R的纯左理想, 则由条件知I是(m,n)-投射左R-模.设N是(m,n)-内射左R-模, 则由正合列

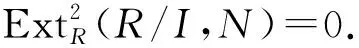
充分性.设I是R的纯左理想, 则存在纯正合列ε: 0→I→R→R/I→0.由文献[13]中推论4.86知,R/I是平坦模, 于是由条件知(m,n)-pd(R/I)≤1.设N是(m,n)-内射左R-模, 考虑正合列

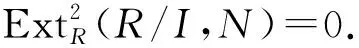
根据文献[2], 记循环平坦左R-模的类为CF, 即CF={R/I|I是R的纯左理想}.令

PI=CF⊥, PP=⊥PI,

其中：

根据文献[14], 如果对任意的(n,m)-表现左R-模M, 序列HomR(M,B)→HomR(M,C)→0正合, 则称左R-模的短正合列0→A→B→C→0是(m,n)-纯正合的.如果0→N→M→M/N→0是(m,n)-纯正合列, 则称左R-模M的子模N是(m,n)-纯子模.

定理2设R是环.则下列条件等价:

1)R是左(m,n)-纯遗传环;

2) 对任意的内射左R-模E及E的任意(n,m)-纯子模N,E/N∈PI;

3) 对任意的M∈PP,M的第0个合冲是(m,n)-投射的;

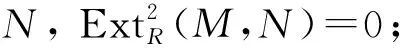
5) 对任意的M∈PP, (m,n)-pd(M)≤1.

因为R是左(m,n)-纯遗传环, 所以I是(m,n)-投射的.于是由文献[6]中定理1知, 存在左R-同态h:I→E, 使得f=πh.又因为E是内射左R-模, 所以存在左R-同态g:R→E, 使得h=gi.故f=(πg)i, 因此E/N∈PI.

其中P是投射左R-模.设

是(n,m)-纯正合列, 其中E是内射左R-模.考虑下图:

其中f是左R-同态.由条件2)知E/N∈PI.而M∈PP, 所以存在左R-同态g:P→E/N, 使得f=gα.又因为P是投射左R-模, 所以存在左R-同态h:P→E, 使得g=βh.故f=βhα.由文献[6]中定理1知,K是(m,n)-投射的.

0→K→P→M→0,

其中P是投射左R-模.由条件3)知K是(m,n)-投射的.于是由正合列