Canopy在划分聚类算法中对K选取的优化
2020-05-29王海燕崔文超许佩迪
王海燕, 崔文超, 许佩迪, 李 闯
(1.长春大学 计算机科学技术学院, 长春 130022; 2.吉林师范大学 计算机学院, 吉林 四平 136000)
Canopy算法是一种简单、快速、准确的对象聚类方法[1], 可应用于Hadoop平台[2].该算法可将所有对象都表示为多维特征空间中的一个点, 采用快速近似距离度量和两个距离阈值比较方式, 实现快速粗聚类.聚类算法[3]应用广泛, 目前对聚类算法的效率与准确度的研究已有许多结果[4-5].但当数据变大时, 聚类难度也加大.数据变大有多种情况: 数据条目多, 则整个数据集包含的样本数据向量多; 样本数据向量维度大, 包含多个属性; 要聚类的中心向量多等.当所应用聚类算法的数据遇到上述情况时, 聚类K值的取值准确性便尤为重要.在划分聚类算法中, 准确的K值可有效提高聚类工作的效率.Canopy算法将数据划分成可重叠的子集, 通过快速近似比对处理, 可为K均值聚类提供K值的预判.本文通过对Canopy算法进行优化, 可更好地实现在划分聚类算法中聚类数K的预判, 减少试探取值的工作量, 从而减少聚类工作时间, 提高工作效率.
1 传统Canopy算法
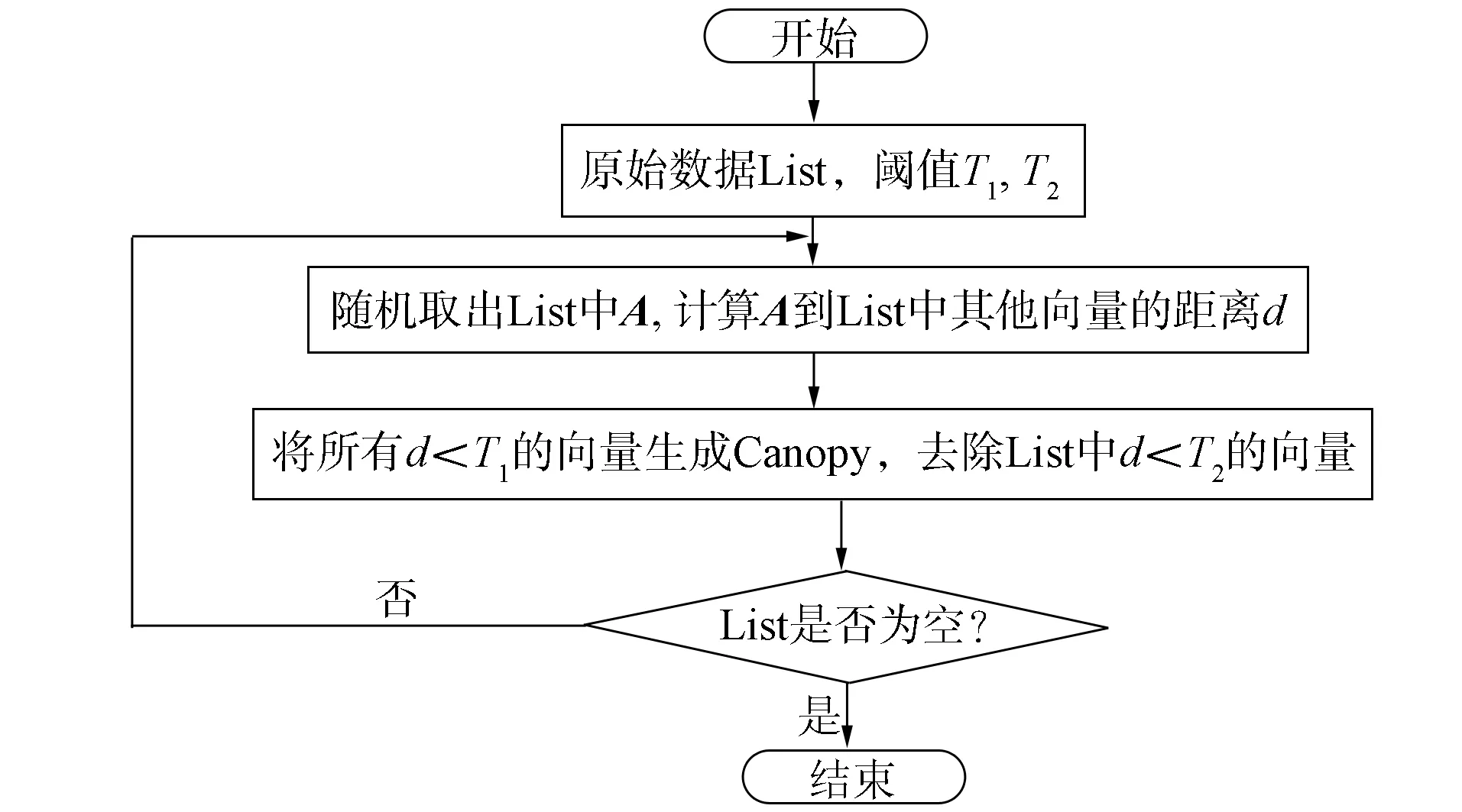
图1 Canopy算法流程Fig.1 Flow chart of Canopy algorithm
Canopy算法的主要思想是把聚类分为两个过程[6]: 首先通过使用一个简单、快捷的距离计算方法将数据分为可重叠的子集, 每个子集是一个“Canopy”; 然后通过使用一个精准、严密的距离计算方法计算出现阶段中同一个Canopy的所有向量的距离.这种聚类方法使用了两种距离参与计算, 由于只计算了重叠部分的数据向量, 因此可达到减少计算量的目的.
Canopy算法的优势主要表现在两方面: 1) 通过粗略距离计算把数据划入不同可重叠子集中; 2) 只计算在同一重叠子集中的样本数据向量, 减少了需要距离计算的样本数量.Canopy算法流程如图1所示.由图1可见, 需要从List中随机取点, 因此存在噪声点和孤立点.此外, 算法还需要距离阈值T1,T2参与运算, 因此获取一个适合当前List的阈值是优化的关键.
2 Canopy算法优化
2.1 方法描述
针对Canopy算法在聚类数K值预判过程中的缺陷, 将优化重点放在选取特殊的聚类中心点和获取阈值T1,T2上.下面根据Python语言实现Canopy算法的优化.
1) 将距离数据均值点最近点作为聚类中心点, 可尽量消除噪声点和孤立点对聚类效果的影响, 并消除随机取点对聚类数K的影响.
2) 优化阈值获取方式.由于原始阈值T1,T2是通过任意取值得到的, 因此通过优化阈值选取方式, 可减少阈值选择的盲目性.阈值获取方式有多种: 一是通过计算数据点到均值点的最远距离L1和最近距离L2确定T1和T2; 二是通过Canopy列表、移除列表中的元素个数、移除率(删除列表元素个数/Canopy列表元素个数)和聚类效果图调整T2的大小.若前几次聚类的移除率太小, 则增大T2; 若移除列表和Canopy列表中的数据点个数小于总数据集个数的5%且增大T2值后聚类效果更佳, 则增大T2; 最后, 根据聚类效果图得出T2的最终值并参与实验, 得出合适的聚类数K.优化Canopy算法实现了准确预判聚类的个数.
2.2 Canopy+算法
Canopy+算法主要从阈值获取方式和初始聚类中心的选取两方面进行优化.阈值T1,T2的获取: 通过遍历所有数据, 取所有数据点的均值点, 计算均值点到所有数据点的距离, 最远距离记作L1, 最近距离记作L2, 并将L1-L2赋值给T1, 将L1/2赋值给T2; 初始聚类中心通过选取与均值点最近的点得到.两方面的优化使预判出的聚类数K更准确.在阈值T1,T2获取过程中,T2是不断修订的, 本文需将删除率控制在一定范围内.删除率过大说明T2过大, 删除率过小说明T2较小.
Canopy+算法步骤如下:
1) 计算List原始数据的均值点, 将距离均值点的最远距离记作L1, 最近距离记作L2, 并将L1-L2赋值给T1, 将L1/2赋值给T2;
2) 取距离均值点最近点作为算法的聚类中心, 计算该中心与其他样本数据向量之间的距离d;
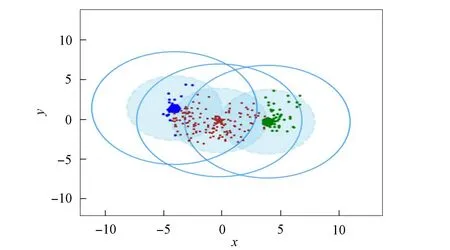
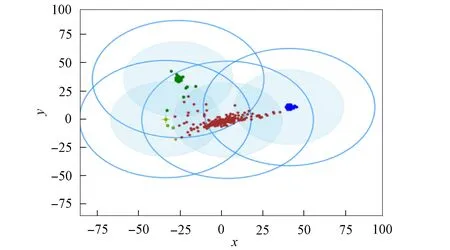
3) 将距离d 4) 根据聚类效果图、移除率和Canopy列表、移除列表中的元素个数再次调整阈值T2; 5) 重复步骤2)和3), 直到候选中心向量名单为空, 即List为空, 算法结束. 本文以2DIris数据集和New-thyroid数据集为例进行Canopy算法和Canopy+算法的对比实验.Iris和New-thyroid数据集都是UCI标准数据库[7]中的数据集, UCI是一个常用的标准测试数据集库, 可用于机器学习, 该数据库目前有335个数据集.3种数据集信息列于表1. 表1 数据集信息 2DIris数据集的可视化界面如图2所示.由图2可见, 数据集聚类类别较明显, 聚类后结果与实际分类结果相符.图3是New-thyroid数据集进行主成分分析(PCA)降维[8]后的二维效果图, 通过实验分析, New-thyroid数据集的二维聚类效果与原数据聚类结果一致. 图2 2DIris数据集可视化结果Fig.2 Visualization results of 2DIris data set 图3 New-thyroid数据集可视化结果Fig.3 Visualization results of New-thyroid data set 通过优化方法计算2DIris数据集的初始阈值T1,T2及其他数据.通过Canopy+算法计算得到T1,T2的初始值分别为3.22和1.6, 通过阈值T1,T2得到的聚类移除率分别为0.425,0.97,1, 对应每个移除列表的元素个数分别是63,34,49, 每个Canopy的元素个数分别为148,35,49, 数据集的聚类个数为3.由于移除率不足以改变T2, 因此阈值T1,T2的终止值不变, 实验结果如图4所示.由图4可见, Canopy+算法对2DIris的聚类界限明显, 可见效果较好, 聚类个数与实际类别个数一致, 聚类效果与其实际分类效果相符.使用优化过程中计算的T1,T2对Canopy算法进行实验, 结果如图5所示.与图4相比, Canopy算法的聚类边界不清楚, 聚类效果不理想, 且聚类数K易出现误差. 图4 Canopy+对2DIris数据集的效果Fig.4 Effect of Canopy+ on 2DIris data set 图5 Canopy对2DIris数据集的效果Fig.5 Effect of Canopy on 2DIris data set 优化方法计算New-thyroid数据集得出的初始阈值T1,T2及其他数据信息列于表2.初始的阈值T2对实验结果有影响, 且移除率满足调整T2的条件, 因此需要重新设置.当T2=25时, 存在2个Canopy列表的元素个数小于数据集元素个数的5%, 故增大T2的值; 当T2=30时, 存在其中1个Canopy列表只有2个元素, 继续增大T2; 当T2=35时, 聚类个数发生了变化, 但仍存在2个Canopy列表的元素个数过少, 继续增大T2值; 当T2=40时, 聚类个数停止改变, 并根据聚类的效果图得出这两个聚类不能因为T2的增大而忽略.因此, 通过效果图再次调整T2的大小得到最终值, 聚类效果如图6所示. 表2 New-thyroid数据集的实验数据 将最终的T1,T2应用于Canopy算法得到的效果如图7所示.由图7可见, 图6中聚类界限分明, 聚类数预判稳定; 而Canopy算法聚类效果与Canopy+算法的聚类效果相比, 聚类界限模糊, 在聚类个数预判上只能取近似值.因此, Canopy+算法的聚类更理想, 聚类个数的预判更准确. 图6 Canopy+对New-thyroid数据集的效果Fig.6 Effect of Canopy+ on New-thyroid data set 图7 Canopy对New-thyroid数据集的效果Fig.7 Effect of Canopy on New-thyroid data set 应用UCI数据库中的Seeds数据集, Seeds数据集包含210条数据, 共有7个属性, 分别是area A,perimeter P,compactness C,length of kernel,width of kernel, asymmetry coefficient,length of kernel groove.为更好实现数据的可视化, 在不影响数据聚类效果的前提下, 通过PCA技术进行多维数据降维操作, 降维后的二维数据点如图8所示. 图8 Seeds数据点Fig.8 Data points of Seeds 图9 最终实验效果Fig.9 Final experimental effect 选取距离中心点最近点作为初始点, 计算得出阈值T1, 根据T1估算阈值T2的大小, 再根据移除率、移除列表元素个数、Canopy列表元素个数和聚类效果图, 最终确定阈值T2的值及聚类个数K的值, 其数据信息列于表3.本文根据表3数据进行实验, 其最终效果如图9所示.由图9可见, 聚类数为3时的聚类效果较理想. 表3 Seeds实验数据信息 综上所述, 本文在Canopy算法基础上进行优化, 提出了一种Canopy+算法, 实现了对划分聚类算法[9]聚类数K的预判.Canopy+算法通过距离、删除率等参数进行阈值T1,T2的设定, 并不断调整, 直到确定阈值, 进一步对聚类个数进行预判.实验结果表明, Canopy+算法预判出了准确的聚类个数, 减少了试探取值的个数, 进而降低了聚类工作量, 减少了聚类工作的时间, 提高了工作效率.3 实验测试
3.1 数据集获取

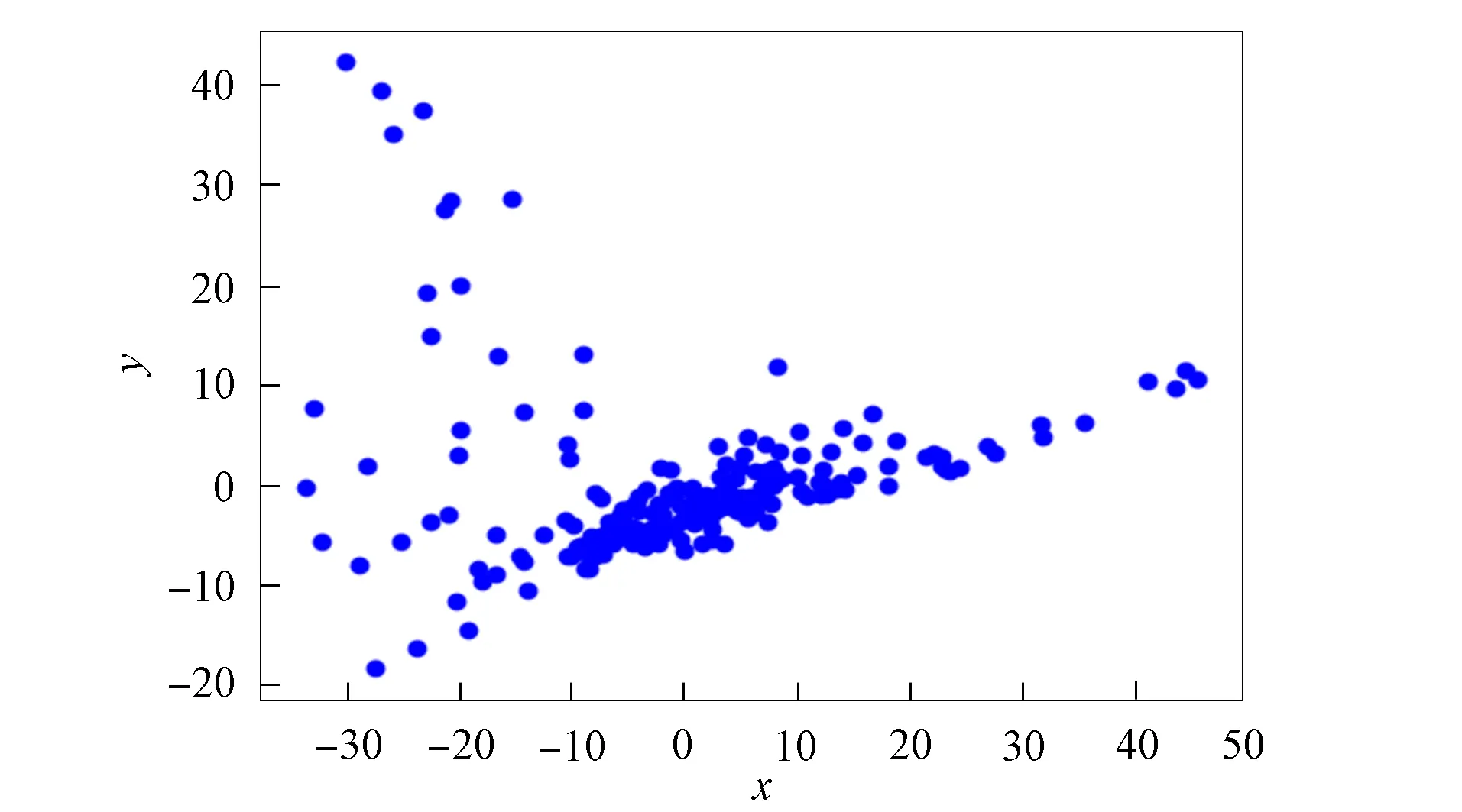
3.2 2DIris的聚类数预判过程
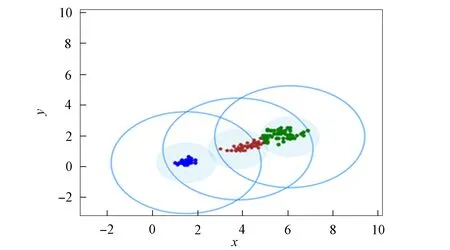
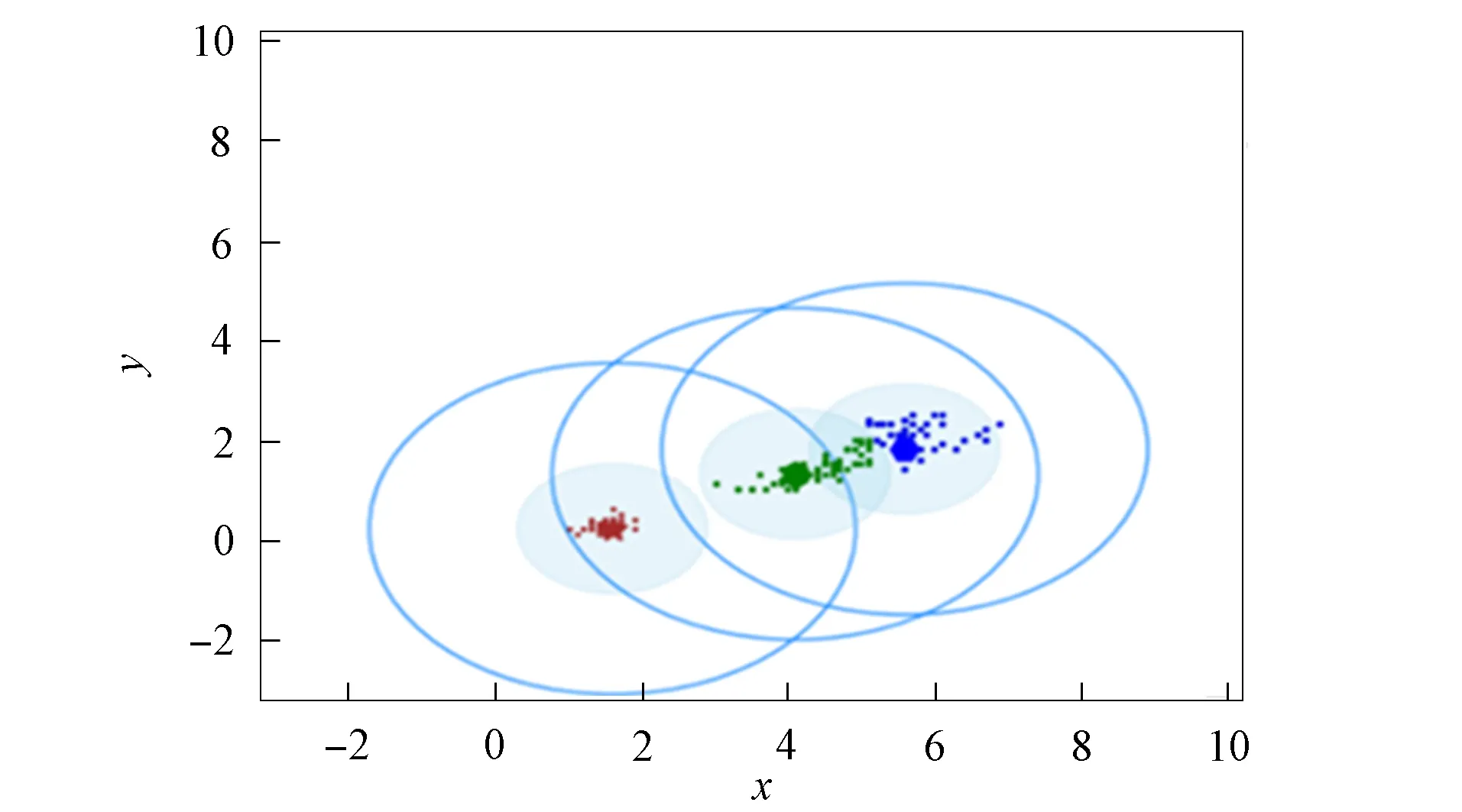
3.3 New-thyroid数据集的聚类数预判过程

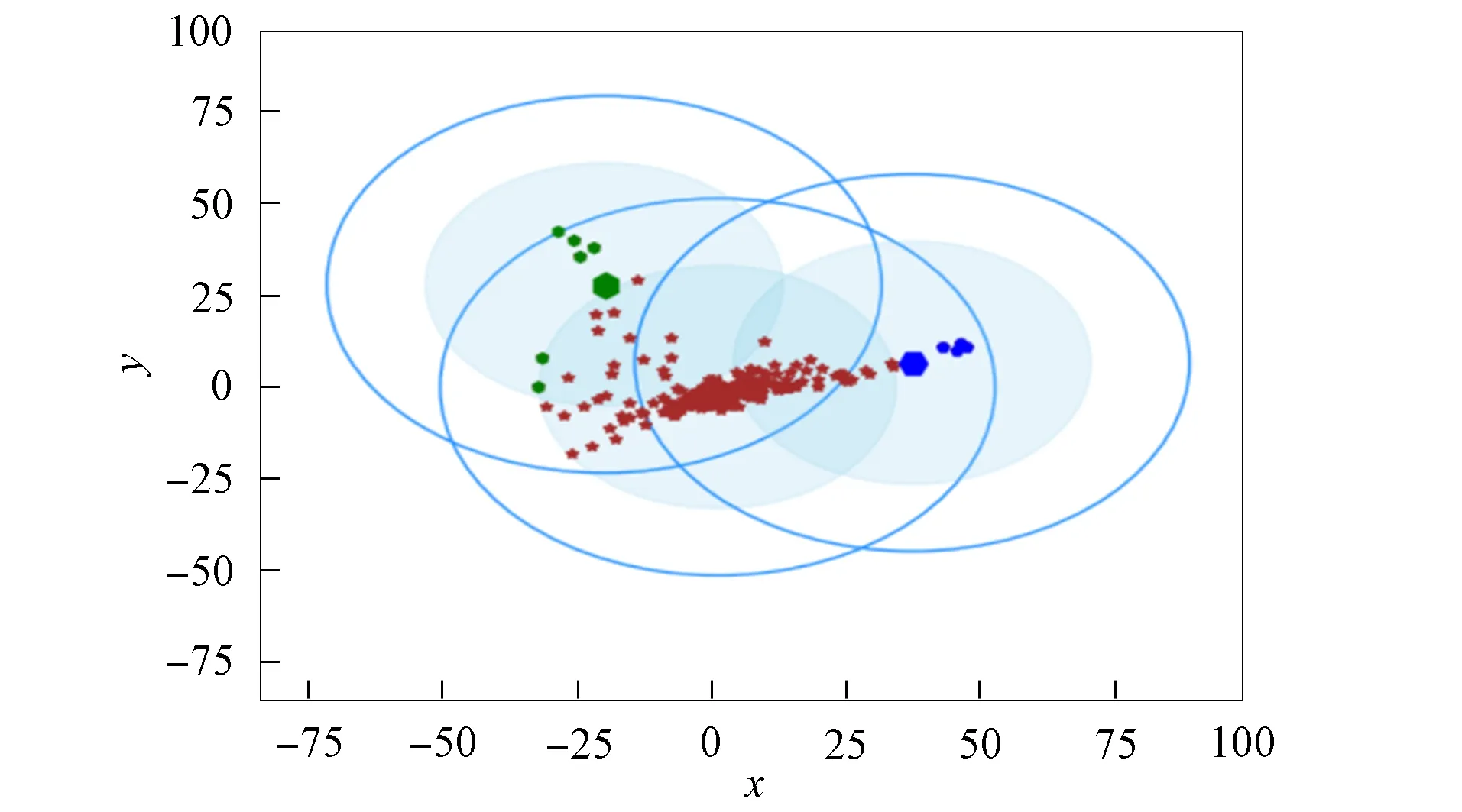
4 Canopy+算法对K值预判的应用
4.1 数据集选择及处理
4.2 Canopy+算法实现K值预判