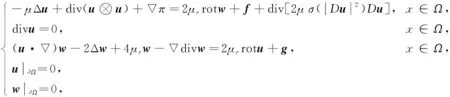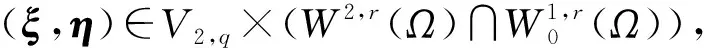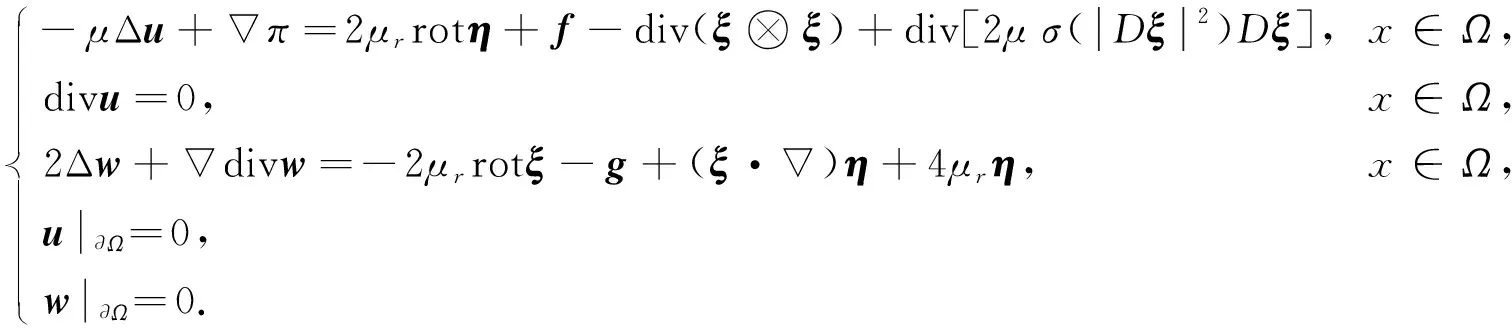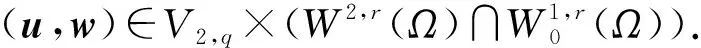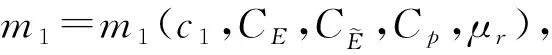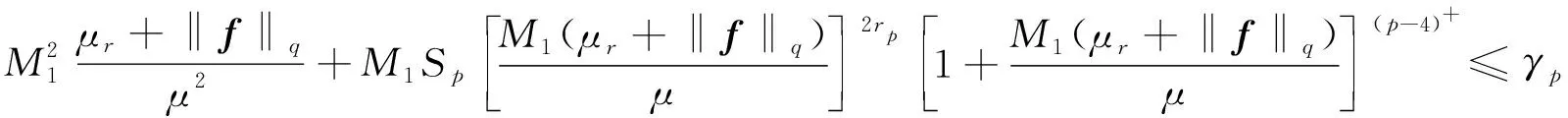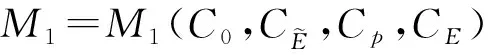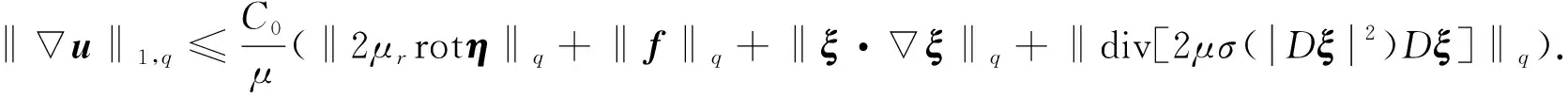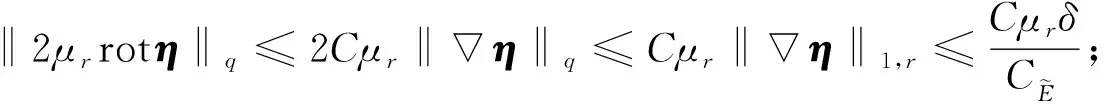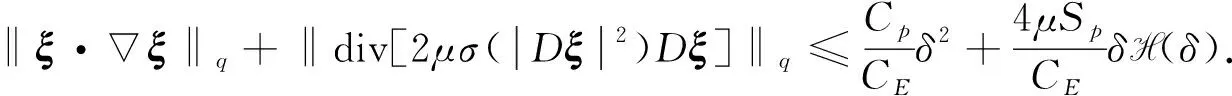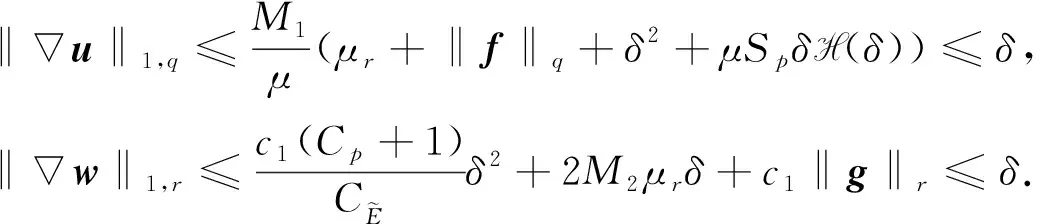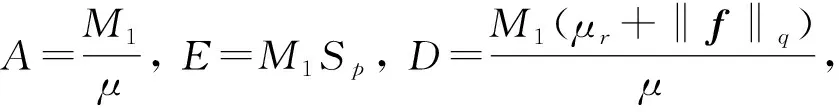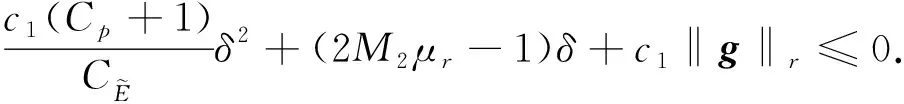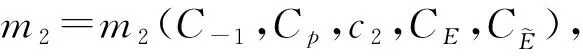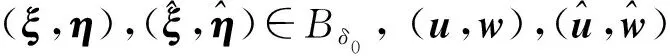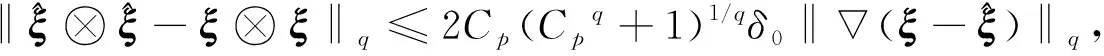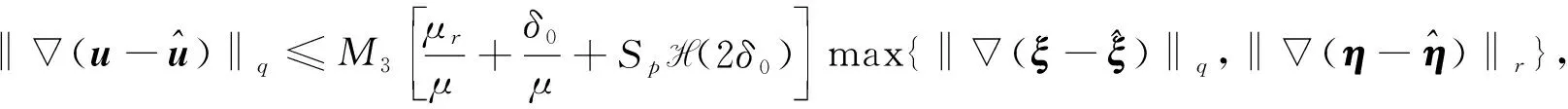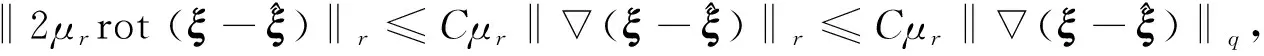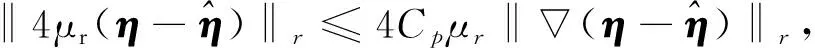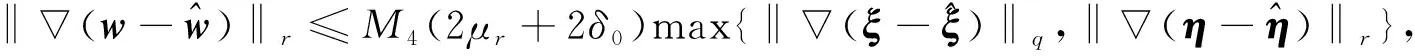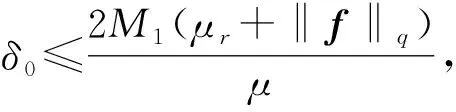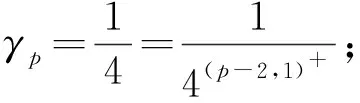一类非Newton微极流体方程组强解的存在唯一性

史伟伟, 王长佳, 高艳超

(长春理工大学 理学院, 长春 130022)

1 引言与主要结果

微极流体模型[1]是对经典Navier-Stokes方程的推广, 它考虑了流体颗粒的微观结构.物理上, 微极流体可表示由悬浮在黏性介质中的刚性随机取向粒子组成的流体[2], 如悬浮液、润滑剂、动物血液以及液晶流体等.

令Ω⊂n(n=2,3)为一光滑有界区域, 考虑如下非Newton微极流体方程组的Dirichlet问题:

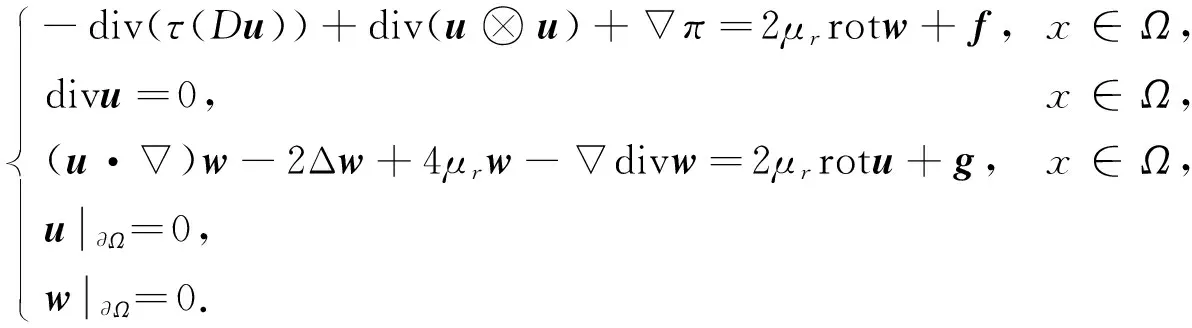
(1)

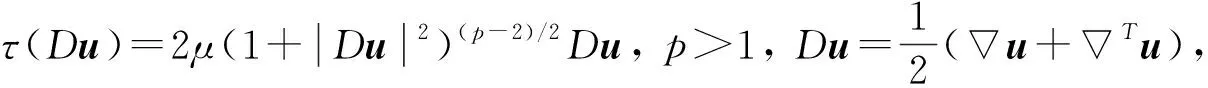
对于系统(1), 若p=2, 则其退化为经典的Newton型微极流体模型, 关于其存在唯一性的研究目前已有很多结果[3-7]; 若p≠2, 则系统(1)成为非Newton微极流体模型.Araújo等[8]通过结合使用Galerkin方法与紧性方法证明了其弱解的存在性, 并讨论了解的唯一性与周期性结果； 文献[9]在二维光滑有界区域上讨论了其解的渐近性, 并证明了系统拉回吸引子的存在性以及关于黏性系数的上半连续性.

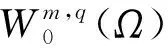
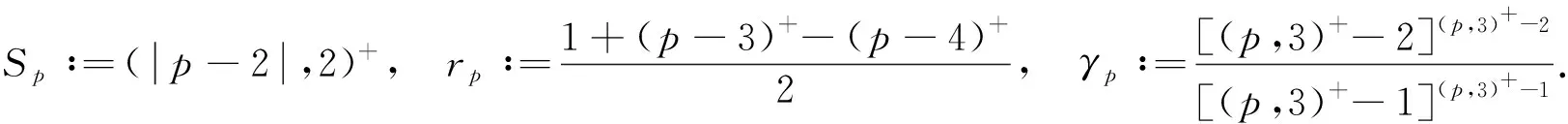
(2)

引入空间

对于q>r>n和δ>0, 用Bδ表示下列凸集：

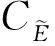
‖(ξ,η)‖1,q,r∶=max{‖ξ‖1,q,‖η‖1,r}.

定义1如果下列积分等式成立:

则称u∈Vp,w∈W01,q(Ω)为问题(1)的弱解.

本文主要结果如下.

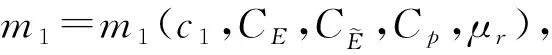
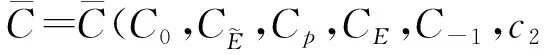
2 引 理

引理1[10]设m≥-1为一个整数,Ω⊂n(n=2,3)为一个有界区域, 边界∂Ω∈Ck, 其中k=(m+2,2)+.则对∀ψ∈Wm,ρ(Ω), 方程组

存在唯一解[u,π]∈Wm+2,ρ(Ω)×Wm+1,ρ(Ω), 且估计式

‖u‖m+1,ρ+‖π‖m+1,ρ/≤Cm‖ψ‖m,ρ

成立, 其中Cm=Cm(n,ρ,Ω)是一个正常数.

引理2[11]设rp,γp由式(2)给出, 定义函数G:+→如下：

G(δ)=Aδ2-δ+EδH(δ)+D,

其中A,E,D是正常数, H(x)=x2rp(1+x)(p-4)+.如果不等式

AD+ED2rp(1+D)(p-4)+≤γp

成立, 则G至少有一个根δ0, 且δ0>D.此外, 对每个β∈[1,2], 下列估计式成立：

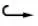
‖T(u)-T(v)‖Y≤K‖u-v‖Y, ∀u,v∈B, 0

则T在B上存在唯一不动点.

3 主要结果的证明

下面应用不动点定理(引理3)给出定理1的证明.首先, 将问题(1)重写如下：

(4)

(5)

T: (ξ,η)→(u,w).

下面证明对某个δ0>0,T为一个Bδ0到其自身的压缩映射.

(6)

证明: 设(ξ,η)∈Bδ.由引理1知u∈V2,q, 且有

(7)

对式(7)右端各项, 首先有

(8)

其次由文献[11]中推导, 可得

(9)

综合式(7)～(9)可得

其中

另一方面, 由文献[13]知, 存在常数c1>0, 使得

其中

不妨假设δ≤1, 若使T(Bδ)⊆Bδ, 则需使下列条件成立：

(11)

AD+ED2rp(1+D)(p-4)+≤γp,

在引理2中取β=2, 又可得

其次, 将式(11)中第二个不等式写为

(12)

如果判别式

即

则存在δ使得式(12)成立.

取常数D满足δ-

由于对每个δ∈[δ-,δ+]都有式(12)成立, 故可取δ2∈(δ-,D), 使得下式成立：

综上, 得

因此, 取δ0=δ1, 有T(Bδ0)⊆Bδ0.

其中:

首先, 由引理1, 有

对式(14)右端项, 首先有

(15)

根据文献[11]中推导又有

(16)

(17)

综合式(14)～(17)可得

(18)

其中

M3=max{CC-1(Cp+1),CC-1Cp(Cpq+1)1/q,CC-1}.

另一方面, 由文献[13]知存在c2>0, 使得

对式(19)右端各项计算可得

(20)

(21)

综合式(19)～(22)可得

(23)

其中

结合式(18)与式(23)可得