基于IECP的CTCS-3列控车载TSM曲线完备性测试用例集生成方法研究

郑 伟， 唐 涛， 吕继东， 魏国栋

(1.中铁第五勘察设计院集团有限公司，北京 102600；2.北京交通大学 轨道交通控制与安全国家重点实验室，北京 100044；3.北京交通大学 轨道交通运行控制系统国家工程研究中心，北京 100044)

列控系统作为典型的安全苛求系统，其任何功能故障都可能造成严重的事故和生命财产的损失[1]。车载设备作为列控系统的关键核心技术装置，主要完成列车运行速度的实时超速防护功能。速度-距离模式曲线，以目标速度、目标距离、线路条件、列车特性为基础信息，生成列车安全运行的一次制动模式曲线，是实现列车超速防护功能、确保列车安全运行的关键。然而，列控系统的速度模式曲线具有参数输入域规模大、故障模式复杂等特点，如何完备地验证列控车载设备速度-距离监控曲线功能至关重要。

基于一致性的黑盒测试技术，作为验证和确认系统功能正确性的关键方法，是保证系统功能正确实现的重要手段[2]。人们对测试用例集的评价通常着力于检验其完备性。而完备的测试集需满足：当被测系统行为违反了给定的规范说明(或与参考模型的一致性关系)时，在测试集中必然存在至少一个测试用例在测试中不被通过；当被测系统行为满足给定规范说明(或与参考模型的一致性关系)时，通过测试集中所有测试用例[3]。

国内外学者针对车载设备速度-距离模式曲线功能的测试，进行了广泛的研究。传统的测试方法大多需要手工生成测试用例，效率较低，并具有一定的不确定性。文献[4]提出一种加强的等价类测试方法，并应用于意大利的列车自动控制系统(Automatic Train Control，ATC)中。这种方法基于ATC规范SCMT，其手工生成的测试用例无法将所有的输入作为测试用例来做穷举测试，难以保证在大规模输入域参数条件下的完备性。文献[5]通过组合测试的方法，自动生成了满足ATP速度监控功能需求的测试用例，在保证测试覆盖率的基础上实现了较高的用例约减率，有效提高了测试效率。但由于车载ATP是安全苛求系统的核心设备，所以该方法并不能作为列控系统测试的主流手段。近年来，基于形式模型的一致性测试技术成为研究的热点[6-7]。该技术以形式化理论为基础，通过建立精确的参考模型，自动生成满足相关覆盖准则的测试用例，可以有效地降低测试成本和时间，提高测试的质量[8]。但是为满足测试的完备性要求，大多形式化方法仍会产生大量甚至无穷的测试案例，通过利用等价类划分策略[9]可以较好地解决该问题。文献[10]引入时间自动机进行建模，结合基于模型的等价类划分测试策略，利用W-Method方法最终生成完备性测试用例。文献[11]提出基于模型的等价类划分测试方法，充分考虑了ETCS车载系统中速度-距离模式曲线的特点，通过设计故障模型，并首次应用于顶棚监控(Ceiling Speed Monitor,CSM)测试用例的生成研究，最终成功生成了完备的测试用例集。在利用形式化方法研究列控系统测试用例的自动生成时，国内学者大多着力于运营场景或模式转换的建模[2,12-13]，而针对车载ATP曲线的测试则鲜有成果。

本文以列控系统中的目标速度监控曲线TSM作为被测对象，结合CTCS-3级列控系统需求规范(System Requirement Specification,SRS)，建立了满足司机制动优先和设备制动优先两种不同制动优先级情况下的目标速度监控曲线(Target Speed Monitoring,TSM)有限状态机模型；利用反应式状态近级系统(Reactive State Transition System,RSTS)的形式化语义，描述了不同输入情况下模型的内部状态迁移过程；基于I/O等价原理以及等价类划分测试理论，得出两种不同制动优先情况下的输入等价类化分(Input Equivalence Class Partitioning,IECP)；通过引入被测系统(System Under Test,SUT)的故障模型，确定描述被测系统实际行为模型的故障域范围；最后采用W-method测试用例集生成方法，在满足模型故障域的条件下，最终得到两种不同制动优先的TSM曲线模型完备测试集，并对测试用例生成进行比较分析。

1 CTCS中的TSM曲线

CTCS-3级列控系统是目前我国高速铁路列控系统使用的主流技术，它采用固定闭塞，以目标距离连续控制模式监控列车的运行，实现高速列车运行速度、运行间隔实时监控和超速防护。列控系统根据进路信息、前车位置、安全追踪间隔等，通过无线闭塞中心生成后续列车的行车许可信息，由列控车载设备对列车实时速度进行监督和控制。

速度监控曲线是列车运行过程中所有位置的限制速度所构成的速度-距离曲线，用于监控列车实时速度。该曲线可分为顶棚速度监控区、目标速度监控区和安全距离区。列车在运行过程中一旦触发速度监控曲线，应采取相应的制动措施，限制列车速度，保证行车安全。目标速度监控区内各速度曲线的名称和关系，见图1。

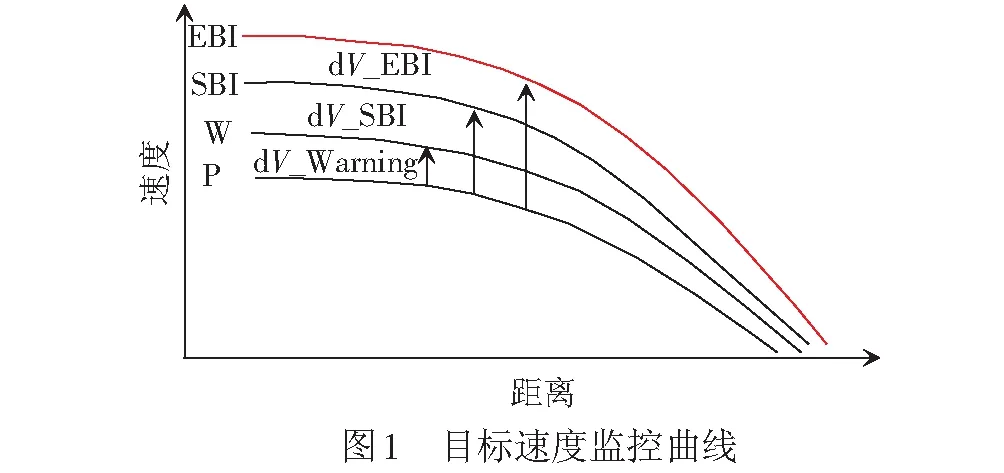
图1中，根据安全制动模型，首先得到紧急制动触发曲线EBI，然后再依次算出常用制动触发曲线SBI、报警曲线W和允许速度曲线P。在任一距离处，这4条曲线的速度值关系为

V_W=VP+dV_Warning

V_SBI=VP+dV_SBI

V_EBI=VP+dV_EBI

在CTCS-3级列控系统目标速度监控防护中，需考虑两种不同制动优先级的情况，即设备制动优先和司机制动优先。这两种制动方式的主要区别在于对常用制动情形的处理。当列车实时运行速度触发常用制动以后，司机制动优先情况下，在满足缓解常用制动的条件时，司机需人工缓解常用制动；相对地，设备制动优先则不需要人为解除制动。设备制动优先方式下，将一个常用制动状态细化为3个不同制动级别的常用制动状态，即弱常用制动(B1N)、中等常用制动(B4N)和最大常用制动(B7N)。

2 基于模型的完备性等价类划分测试理论

如今,有限状态机的建模方法已被广泛应用，但系统的无限输入域问题始终是测试中不可避免的关键点。等价类测试技术可以有效地解决该问题，但是在安全苛求系统的测试中，等价类划分的合理性成为了主要挑战。本文提出一种基于RSTS语义的等价类划分策略以及与其相关的完备测试方法，有效地解决了上述问题。该方法将形式化理论应用于TSM有限状态机，用形式化语义描述状态机的迁移关系，利用状态间的迁移条件合理地实现输入域等价划分，并最终生成了理论上完备的测试集。

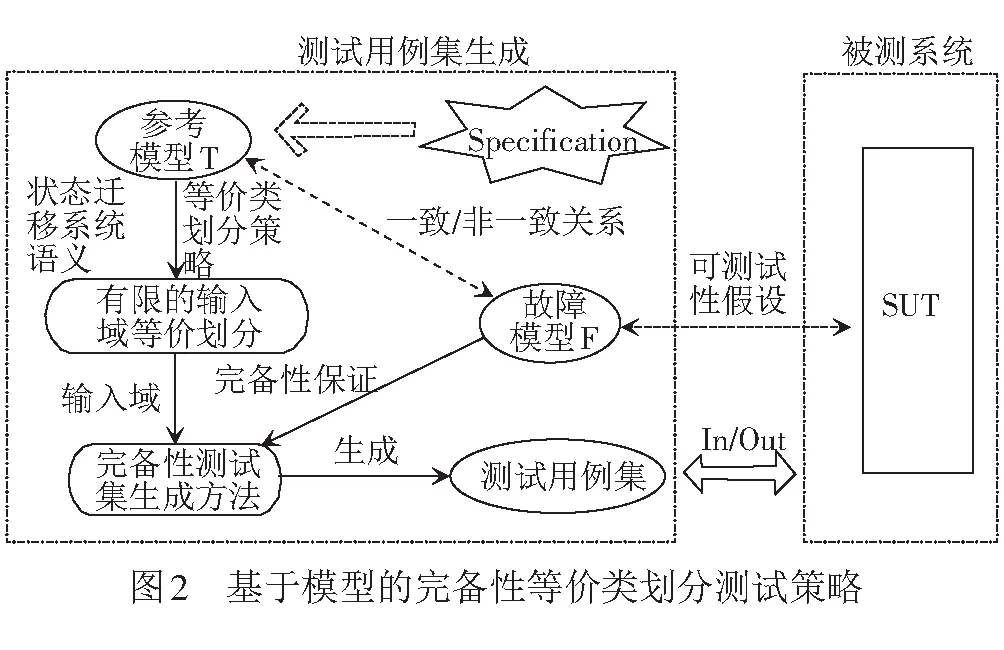
基于模型的完备性等价类划分测试策略见图2。首先，根据被测系统的给定规范建立参考模型，利用有限状态机刻画参考模型的内部状态迁移；然后通过RSTS形式化语义和等价类划分策略，得到有限的输入域划分；最后，根据引入的故障模型，结合完备性测试集生成方法得到满足模型故障域条件下完备的测试用例集。

2.1 系统语义域

状态机模型中，SUT的各种行为都可被反应式状态迁移系统T=(S，s0，R)所表示[14]。其中，S代表状态空间；s0代表初始状态，并满足s0∈S；R代表迁移关系，满足R⊆S×S。定义W为系统的变量空间，并将其划分为输入变量I、内部状态变量M和输出变量O三个部分，即W=I∪M∪O。输入变量空间可为无限域，但内部状态变量和输出变量空间只能为有限域，这样可以保证状态空间能被划分为有限个I/O等价类。相应的，状态空间S中的任一状态s，可表示为变量空间的映射关系。对于s有：W→D，在s状态下的变量w(w∈W)满足s(w)∈D。

将RSTS的状态空间S划分为两种状态集合，分别为静止状态SQ和瞬时状态(或过渡状态)ST。从静态SQ出发的迁移只能改变输入变量的值，且最终迁移到静止状态或者瞬时状态；从瞬态ST出发的迁移必定结束于静止状态，并且这样的迁移只能影响内部状态变量和输出变量。这里，我们假设被测系统的输出值，只能在处于静止状态时才可以被测试环境观测到。

2.2 I/O等价原理

对于两个RSTS系统T和T′，如果给它们同样的输入序列，它们的内部状态相同，且具有相同的可观测输出序列，则称T和T′是I/O等价的，可表示为T～T′[15]。这里的I/O等价并非二者相等。由于假设只有SUT在静止状态时的输出才是可观测的，所以只考虑静止状态时的I/O等价。

2.3 输入等价类划分(IECP)

RSTS的迁移关系R可通过算法表示为[11]

(di,ei)∧(m′,y′)=(m,y)]∨

(di,ei)∧(m′,y′)=(dj,ej)∧(x′=x)]

式中：IDX为系统所有内部状态的索引集合；(di,ei)，i∈IDX为对内部状态变量元组di和输出变量元组ei的枚举;(m,y)为内部变量元组和输出变量元组，满足：若M={m1,…,mk}，则m=(m1,…,mk)；若O={y1,…,yr}，则y=(y1,…,yr)；x=(x1,…,xp)表示输入变量元组，满足I={x1,…,xp}；gi,i为保持在一个瞬时状态的输入条件，gi,j为从一个满足(m,y)=(di,ei)的瞬时状态迁移到另一个满足(m′,y′)=(dj,ej)的静止状态的输入限制条件(其中i≠j)；J为两静止状态间可以进行有效迁移的状态组集合。

结合I/O等价原理，可以得到系统内部迁移状态的I/O等价类Ai，可表示为

Ai={s∈S|[gi,i∧(m,y)=

(di,ei)][s(w)/w|w∈W]}

i=1,…,n

(1)

根据式(1)，可以直观地认为整个有限状态机的状态被分为有限个状态集合，每一个状态集合中的状态都是I/O等价的。

关于对输入条件的限制gi,f(i)，定义为

(2)

根据不同的φf，对输入变量域DI进行有限的划分，可以得到IECPI。

2.4 故障模型

在黑盒测试中，不存在由给定规范(或参考模型)生成的测试用例集，对于SUT的所有可能执行都满足完备性要求，因为不能确定SUT是否仍存在额外的内部状态没有被测试用例集所覆盖。针对这种情况，在基于模型的测试领域中广泛采用的方法是引入故障模型F=(T，～，D(T，m，I))[16]。其中T表示参考模型，具有RSTS的形式化语义；～表示一致性关系(I/O等价)；D为故障域，该集合包含一组可能与参考模型有一致性或非一致性关系的模型；IECPI表示D中模型与T具有相同的输入域划分；正整数m满足m≥n，决定了故障域D的范围，n为T的I/O状态等价类数量，m值越大，D的范围越大。

对于故障域D(T，m，I)中的元素T′，满足：具有同样输入输出变量空间I∪O时，T′应覆盖参考模型T的状态；T′和T具有一致的初始状态 ；T′的I/O状态等价类数量小于等于m。

系统的可测试性假定被测系统的真实行为等价于故障域中某一模型的状态迁移。最终生成的测试集若满足：当且仅当测试集中的所有测试用例都通过和T有一致关系的任一T′∈D，并且若D中存在一个模型不满足与T的一致性关系时，测试集中存在至少一个测试用例不通过,则该测试集关于F是满足完备性要求的。

2.5 生成完备性测试集的方法

对于给定的参考模型T和确定的(m，I)，利用W-Method[17-18]，可以得到确定的有限状态机的完备测试用例集。W-Method生成测试用例集的通用表达形式为

(3)

式中：ω为测试用例的集合；P为需实现参考模型的状态迁移覆盖，用适当的输入序列覆盖整个状态的迁移过程，满足任一状态都可被覆盖，以及从任何状态出发的任何可能的迁移都可以实现；XI为满足输入等价类划分I的任意一组输入序列，n表示T最终的I/O等价类数量，变量m满足m≥n，保证生成的测试用例集的完备性，m-n决定了测试输入序列的长度；W为一组输入集合，要求其中最少有一个元素可以区分状态迁移过程中任意两个状态，即对于不同的状态产生不同的输出序列。

3 生成TSM完备的等价类划分测试集

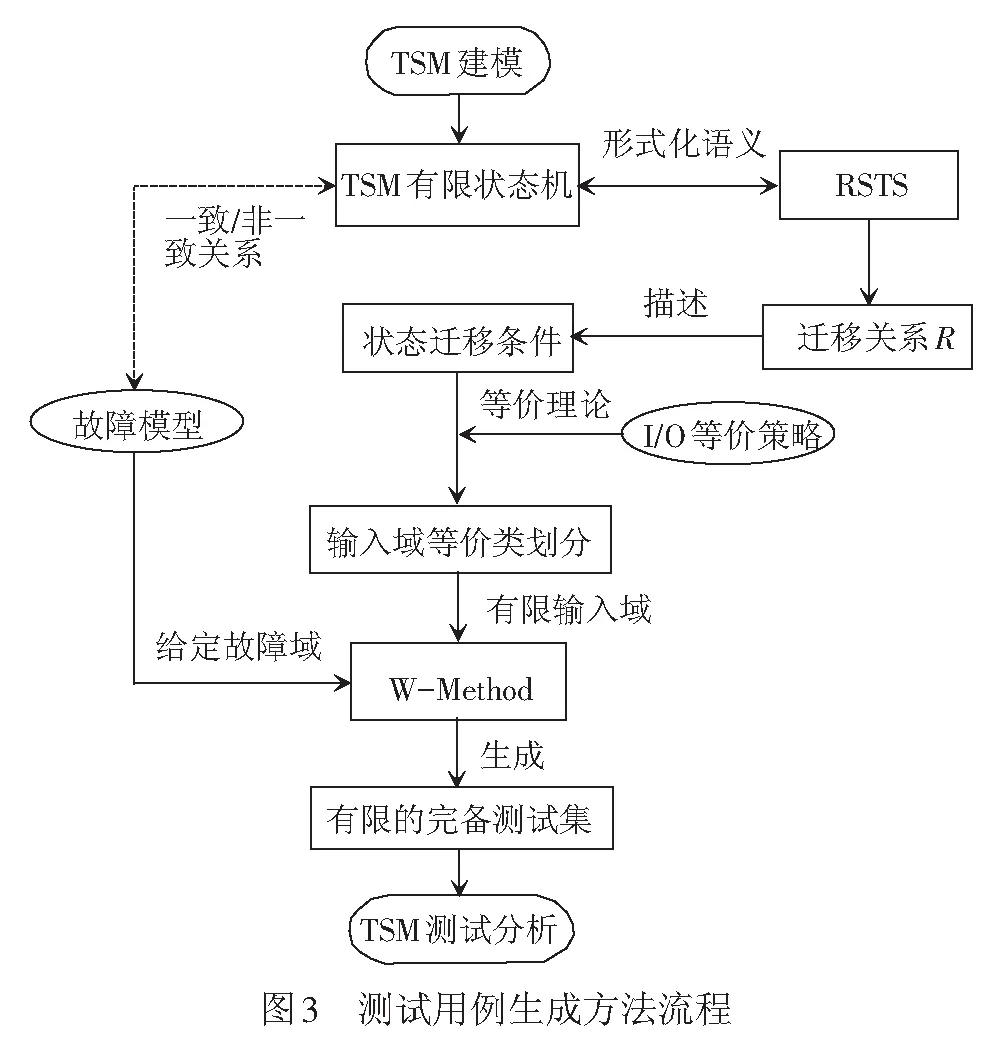
利用基于模型的输入等价类划分测试方法，将上节中提到的一整套形式化理论应用于TSM的测试用例自动生成研究中，其方法流程见图3。

3.1 TSM测试模型接口

根据TSM的功能需求分析建立基于系统建模语言的测试模型，将被测系统视为一个黑盒，测试模型的系统接口见图4。图4中≪SUT≫表示被测系统TSM，≪TE≫表示外界给予输入的测试环境。

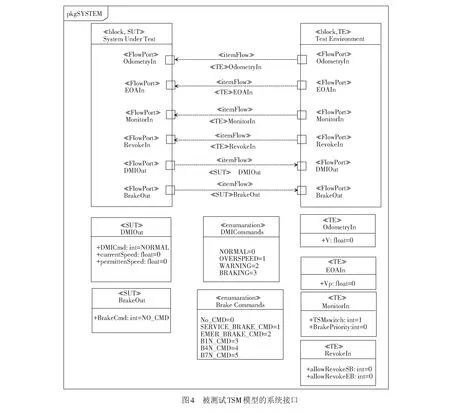
其中被测系统包含4个输入接口：

(1) “OdometryIn”为被测系统提供当前列车的实时速度V。

(2) “EOAIn”提供目标速度监控的行车许可终点(end of authority,EOA)，根据EOA的值可以依次算出EBI、SBI、W和P。而目标速度监控曲线的主要任务就是比较车载安全计算机计算的实时速度V是否满足V≤VP，当列车当前速度V超过VP时，将可能触发报警或者制动行为。

(3) “MonitorIn”中包含2个输入变量，TSMswitch=0表示当前模型是在CSM防护模式下，TSMswitch=1表示在TSM防护模式下，文中暂且只讨论后一种情况；BrakePriority代表不同的制动优先控制方式，0表示设备制动优先情况，1表示司机制动优先情况。

(4) “RevokeIn”包含2个不同的输入变量，用于区分不同制动优先级情况下的允许缓解命令。allowRevokeSB=1表示司机制动优先情况下，解除常用制动的允许缓解命令；allowRevokeEB=1表示两种制动方式下，触发紧急制动命令以后，当列车速度降至0时，允许缓解紧急制动命令。

此外，被测系统还有2个输出接口，分别表示人机交互命令和制动命令：

(5) “DMIOut”中的currentSpeed指列车的当前速度，即currentSpeed=V；permittenSpeed指列车允许速度，即permittenSpeed=VP；DMICmd指人机交互界面的状态命令。

(6) “BrakeOut”表示制动命令，包含了两种不同制动优先级情况下所有可能的命令形式。EMER_BRAKE_CMD表示紧急制动命令，SERVICE_BRAKE_CMD表示司机制动优先情况下常用制动命令，B1N_CMD、B4N_CMD和B7N_CMD分别表示设备制动优先情况下的弱常用制动命令、中等常用制动命令和最大常用制动命令。

3.2 TSM有限状态机模型

通过对TSM防护曲线的分析，针对两种不同制动优先级情况(BrakePriority的不同取值区分)，分别讨论TSM状态机的内部状态迁移过程。

3.2.1 司机制动优先

此时BrakePriority=1，TSMswitch=1。通过目标速度监控区内的不同曲线，将整个TSM监控区划分为5个状态区，得到符合规范要求的状态迁移过程，见图5。

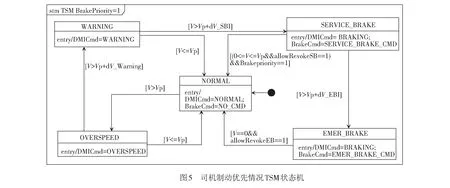
图5中，其执行过程从初始状态NORMAL开始，此状态下输出人机交互界面显示DMICmd=0，无制动命令，BrakeCmd=0。当列车的实时速度超过允许速度(V>VP)，状态机由NORMAL迁移到OVERSPEED状态，输出人机交互界面显示DMICmd=1，无制动命令。当列车实时速度超过报警曲线W(V>VP+dV_Warning)，状态机迁移到WARNING状态，输出人机交互界面显示DMICmd=2，无制动命令。当列车实时速度超过SBI，状态机迁移到SERVICE_BRAKE状态，此时输出人机交互界面显示DMICmd=3，常用制动触发BrakeCmd=SERVICE_BRAKE_CMD。当列车实时速度超过EBI，状态机迁移到EMER_BRAKE状态，输出人机交互界面显示DMICmd=3，紧急制动触发。当在常用制动和紧急制动时，在满足缓解制动条件下，都需司机人工缓解，故状态缓解的迁移条件均得满足allowRevokeSB==1。

3.2.2 设备制动优先

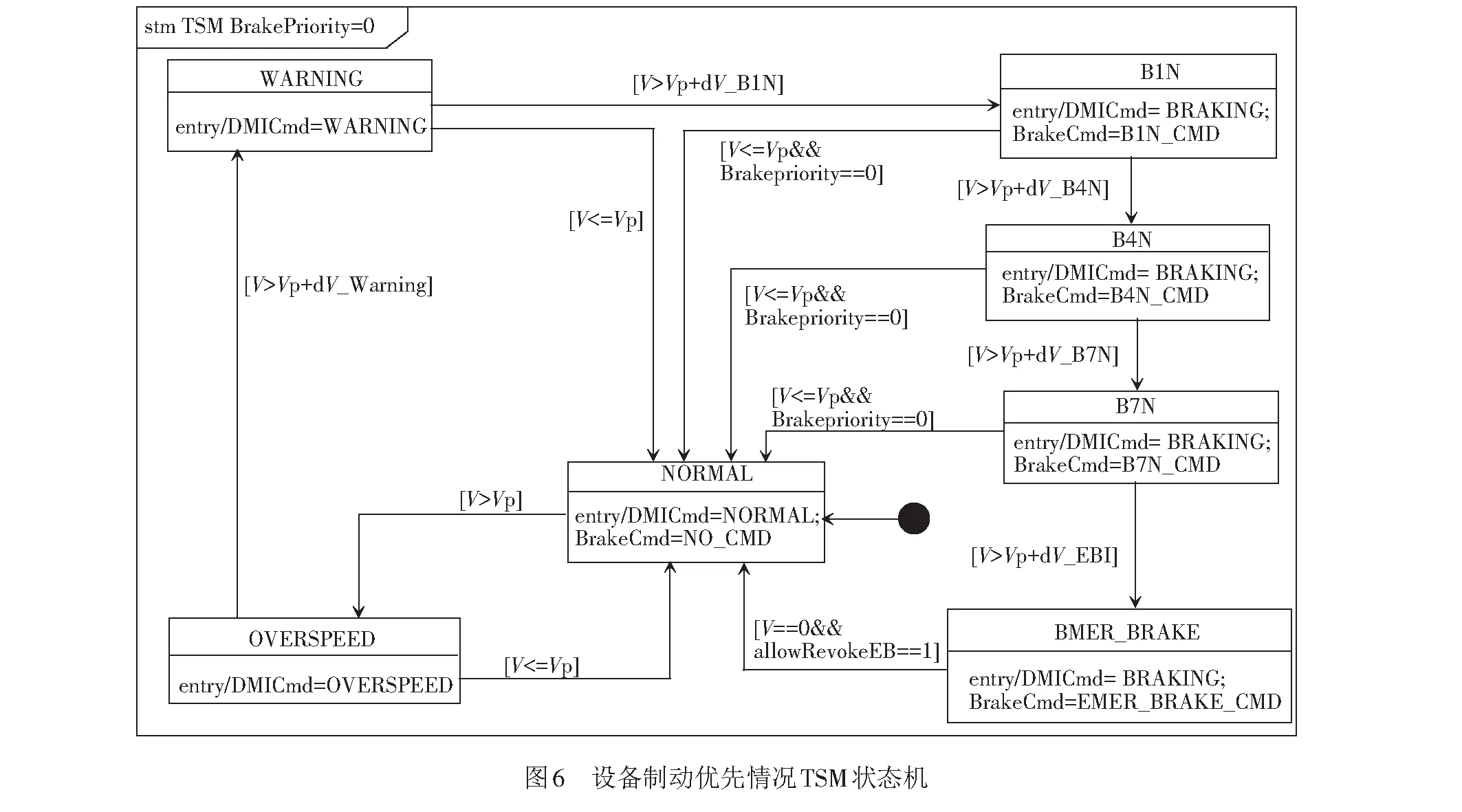
此时BrakePriority=0，TSMswitch=1。相较于人控优先的制动方式，设备制动优先的目标速度监控曲线将SBI细分为B1N、B4N、B7N，相应的状态机增加到7个状态。设备制动优先情况下的TSM状态机见图6。

当列车实时速度满足V>VP+dV_B1N时，状态可由非制动状态迁移到B1N状态，输出人机交互界面显示DMICmd=3，B1N触发BrakeCmd=B1N_CMD。同理，当列车实时速度满足迁移往B4N和B7N状态的条件时，状态机发生迁移，输出人机交互界面显示DMICmd=3及相应触发的制动命令。B1N、B4N和B7N状态满足解除制动条件即V≤VP时，可迁移到NORMAL状态。

需要说明的是，不同状态机满足特殊的瞬时状态迁移。比如在初始状态时，由于测距等问题，导致车载安全计算机算出的实时运行速度直接超过了EBI，触发紧急制动，即由NORMAL出发的下一个静止状态为EMER_BRAKE。在此过程中，由于迁移条件早已满足，所以可将中间状态视为瞬时状态。所以，TSM状态机中的基本状态既可做静止状态也可做瞬时状态。

3.3 生成完备的IECP测试集

3.3.1 模型变量域说明

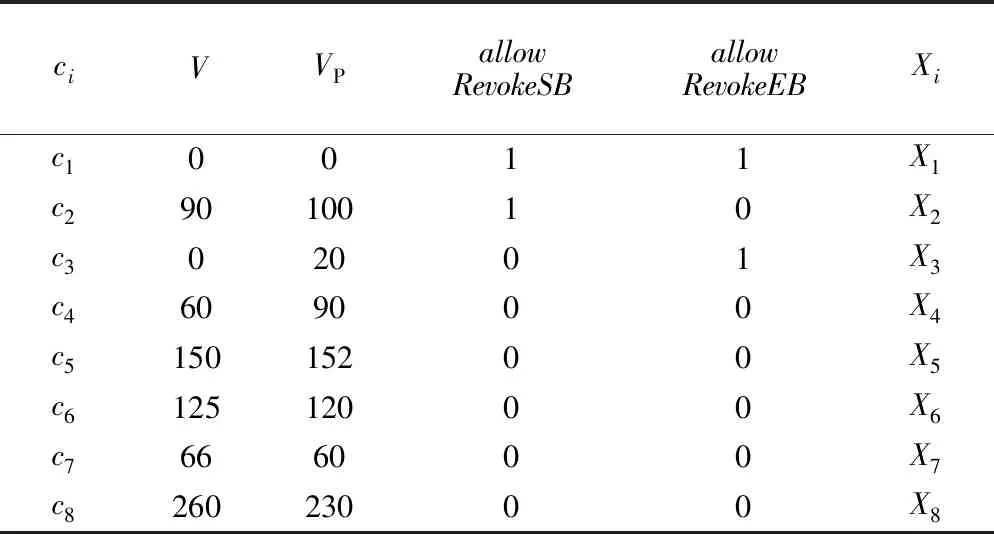
在被测系统中，输入变量I={V,VP,allowRevokeSB,allowRevokeEB}，内部状态变量M={l}，输出变量O={DMICmd,BrakeCmd}。参考图4中对于变量的定义，使用整形变量对其取值进行枚举。DV=DVP=[0,350];DallowRevokeSB=DallowRevokeEB={0,1};DDMICmd={0,1,2,3};DBrakeCmd={0,1,2,3,4,5};BrakePriority=1：Dl={1,2,3,4,5};BrakePriority=0：Dl={1,2,3,4,5,6,7}。

其中，图5、图6中TSM状态机的内部基本状态通过使用整形变量l(“location”)来描述，内部状态l与输出值的对应关系见表1、表2。

表1 人控优先情况TSM状态机基本状态对应输出

表2 机控优先情况TSM状态机基本状态对应输出

3.3.2 RSTS迁移关系

TSM状态机中的基本状态既可做静止状态也可做瞬时状态。做静止状态时，若满足迁移条件则进行静态之间的迁移，否则保持在该状态；做瞬时状态时，满足特殊的瞬时状态迁移。例如在NORMAL(l=1)状态时，当输入条件满足V≤VP，则保持在此状态，下一个“location”l′=l，输出DMICmd’=DMICmd，BrakeCmd’=BrakeCmd。

下面根据不同制动优先级情况下TSM状态机的迁移过程，分别讨论迁移关系R。

(1) 司机制动优先情况

TSM状态机共有5个基本状态，结合图5中状态迁移过程，可得到表达式R中的IDX和J。

IDX={1,2,3,4,5}

J={(1,2),(1,3),(1,4),(1,5),(2,1),(2,3),(2,4),(2,5),(3,1),(3,4),(3,5),(4,1),(4,5),(5,1)}

通过对状态机中每个基本状态迁移条件的分析，可以得到保持在每个基本状态的输入条件gi,i，即

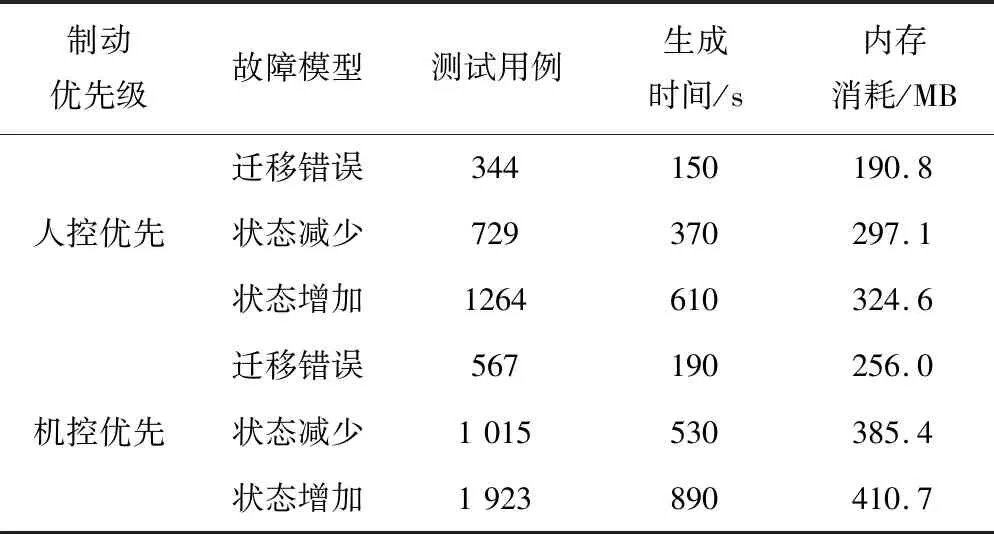
g1,1≡V≤VP

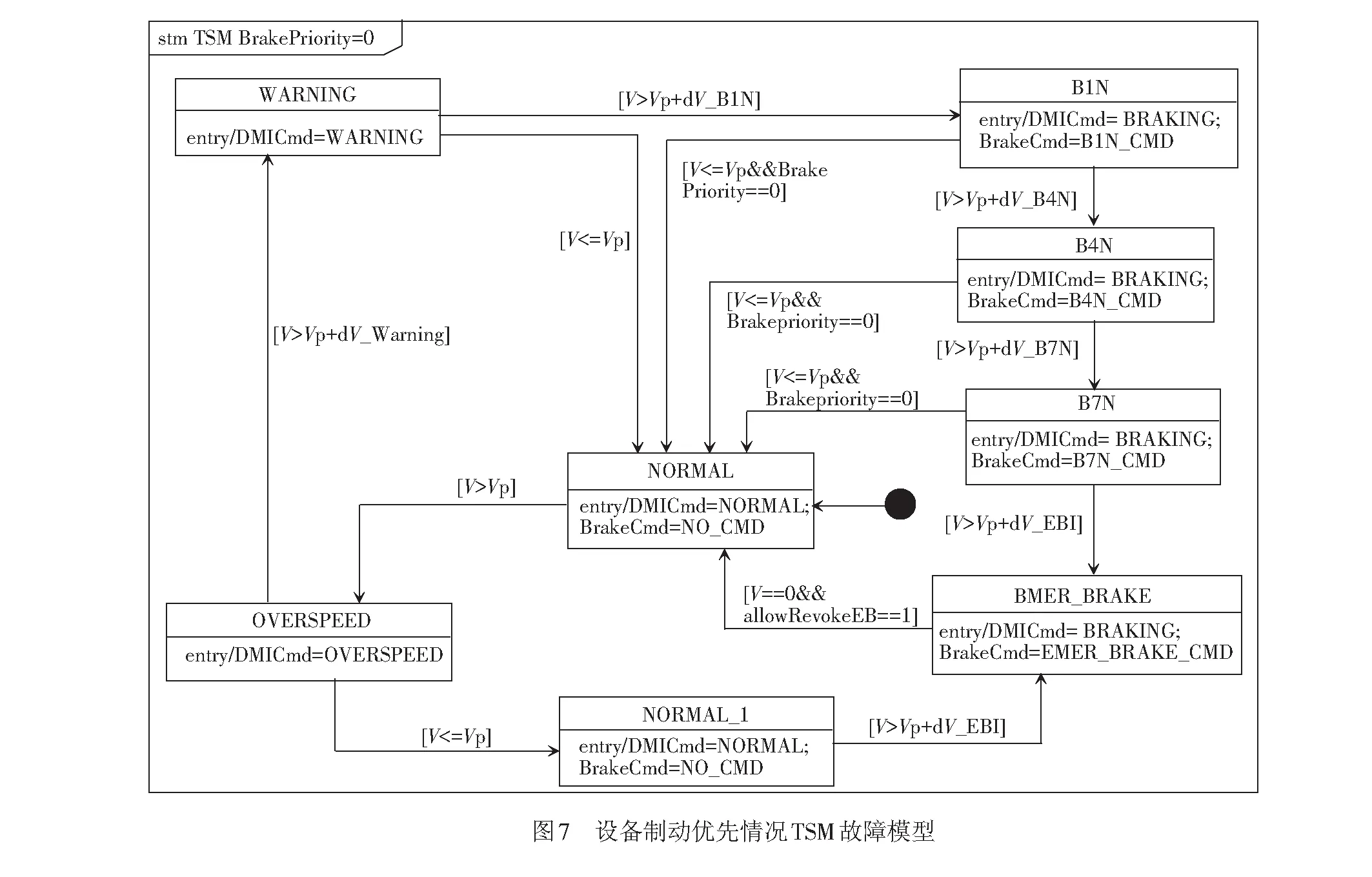
g2,2≡VP

g3,3≡VP

g4,4≡0≤V≤VP+

dV_EBI∧allowRevokeSB=0

g5,5≡V≥0∧allowRevokeEB=0

条件gi,j满足从ST到SQ状态，集合J的内容包含所有符合实际迁移情况的状态组，分析得到所有的gi,j。

g1,2≡VP

g1,3≡VP+

dV_Warning

g1,4≡VP+

dV_SBI

g1,5≡VP+dV_EBI

g2,3≡g1,3

g2,4≡g3,4≡g1,4

g2,5≡g3,5≡g4,5≡g1,5

g2,1≡V≤VP

g3,1≡g2,1

g4,1≡0≤V≤VP∧allowRevokeSB=1

g5,1≡V=0∧allowRevokeEB=1

(2) 设备制动优先情况

TSM状态机共有7个基本状态，结合图6中状态迁移过程，同理可得到状态迁移关系式R中的IDX、J、gi,i和gi,j。

IDX={1,2,3,4,5,6,7}

J={(1,2),(1,3),(1,4),(1,5),(1,6),(1,7),(2,1),(2,3),(2,4),(2,5),(2,6),(2,7),(3,1),(3,4),(3,5),(3,6),(3,7),(4,1),(4,5),(4,6),(4,7),(5,1),(5,6),(5,7),(6,1) (6,7),(7,1)}

通过分析有限状态机的状态迁移过程，可以得到保持在每个基本状态的输入条件gi,i。

g1,1≡V≤VP

g2,2≡VP

g3,3≡VP

g4,4≡VP

g5,5≡VP

g6,6≡VP

g7,7≡V≥0∧allowRevokeEB=0

条件gi,j表示从ST到SQ状态的输入条件，即

g1,2≡VP

g1,3≡VP+dV_Warning

VP+dV_B1N

g1,4≡VP+dV_B1N

VP+dV_B4N

g1,5≡VP+dV_B4N

VP+dV_B7N

g1,6≡VP+dV_B7N

VP+dV_EBI

g1,7≡VP+dV_EBI

g2,3≡g1,3

g2,4≡g3,4≡g1,4

g2,5≡g3,5≡g4,5≡g1,5

g2,6≡g3,6≡g4,6≡g5,6≡g1,6

g2,7≡g3,7≡g4,7≡g5,7≡g6,7≡g1,7

g2,1≡V≤VP

g3,1≡g4,1≡g5,1≡g6,1≡g2,1

g7,1≡V=0∧allowRevokeEB=1

3.3.3 输入等价类划分

(1) 司机制动优先情况

φf≡{g1,1g1,2g1,3g1,4g1,5g2,1g2,2g2,3g2,4g2,5g3,1g3,3g3,4g3,5g4,1g4,4g4,5g5,1g5,5}

(4)

该情况下，根据对φf的定义，利用式(4)，将φf划分为有限个更小的集合:

φ1≡g1,1∧g2,1∧g3,1∧g4,1∧g5,1≡V=0∧allowRevokeSB=1∧allowRevokeEB=1

φ2≡g1,1∧g2,1∧g3,1∧g4,1∧g5,5≡0≤V≤VP∧allowRevokeSB=1∧allowRevokeEB=0

φ3≡g1,1∧g2,1∧g3,1∧g4,4∧g5,1≡V=0∧allowRevokeSB=0∧allowRevokeEB=1

φ4≡g1,1∧g2,1∧g3,1∧g4,4∧g5,5≡0≤V≤VP∧allowRevokeSB=0∧allowRevokeEB=0

φ5≡g1,2∧g2,2∧g3,3∧g4,4∧g5,5≡VP

dV_Warning∧allowRevokeSB=0∧

allowRevokeEB=0

φ6≡g1,3∧g2,3∧g3,3∧g4,4∧g5,5≡VP+

dV_Warning

φ7≡g1,4∧g2,4∧g3,4∧g4,4∧g5,5≡VP+dV_SBI<

V≤VP+dV_EBI∧allowRevokeSB=0∧

allowRevokeEB=0

φ8≡g1,5∧g2,5∧g3,5∧g4,5∧g5,5≡VP+dV_EBI<

V∧allowRevokeEB=0

通过对φf的划分，可以得到对输入变量域的8个等价类划分。定义

Xi={c∈DI|φi[c/

(V,VP,allowRevokeSB,allowRevokeEB)]}

i=1,…,8

(5)

令I={X1,X2,…,X8}，则I为司机制动优先情况下TSM的一个IECP。根据I分析有限状态机的内部状态迁移和输出情况，结果见表3。

从表3可以看出，此前得到的有限状态机并不是最简化的。其中A1～A2，其余Ai两两之间都不满足I/O等价关系，所以在司机制动优先方式下，对于TSM状态机，其最简化的I/O等价类应为{q1=A1∪A2,q2=A3,q3=A4,q4=A5}，其中qi为状态等价类。此外，根据表3中实际的验证能够看到，任何Xi之间都不存在I/O等价关系。因此，I={X1,X2,…,X8}已经是TSM需要的IECP。

表3 司机制动优先情况TSM有限状态机迁移及输出情况

对于具体的测试输入，可选择每个输入等价类中一个符合约束要求的具体值作为输入代表，见表4。这些输入代表的集合称为一组输入集XI。

表4 输入集XI

(2) 设备制动优先情况

同理于司机制动优先方式，先结合该情况下的TSM状态机迁移过程，得到φf。

φf≡{g1,1g1,2g1,3g1,4g1,5g1,6g1,7g2,1g2,2g2,3g2,4g2,5g2,6g2,7g3,1g3,3g3,4g3,5g3,6g3,7g4,1g4,4g4,5g4,6g4,7g5,1g5,5g5,6g5,7g6,1g6,6g6,7g7,1g7,7}

(6)

根据式(6)，可以将φf划分为有限个更小的集合：

φ1≡g1,1∧g2,1∧g3,1∧g4,1∧g5,1∧g6,1∧g7,1≡V=0∧allowRevokeEB=1

φ2≡g1,1∧g2,1∧g3,1∧g4,1∧g5,1∧g6,1∧g7,7≡0≤V≤VP∧allowRevokeEB=0

φ3≡g1,2∧g2,2∧g3,3∧g4,4∧g5,5∧g6,6∧g7,7≡VP

φ4≡g1,3∧g2,3∧g3,3∧g4,4∧g5,5∧g6,6∧g7,7≡

VP+dV_Warning

dV_B1N∧allowRevokeEB=0

φ5≡g1,4∧g2,4∧g3,4∧g4,4∧g5,5∧g6,6∧g7,7≡VP+dV_B1N

φ6≡g1,5∧g2,5∧g3,5∧g4,5∧g5,5∧g6,6∧g7,7≡VP+dV_B4N

φ7≡g1,6∧g2,6∧g3,6∧g4,6∧g5,6∧g6,6∧g7,7≡VP+dV_B7N

φ8≡g1,7∧g2,7∧g3,7∧g4,7∧g5,7∧g6,7∧g7,7≡VP+dV_EBI

根据对φf的划分，得到对输入变量域8个不同的等价类划分。定义

Xi={c∈DI|φi[c/

(V,VP,allowRevokeSB,allowRevokeEB)]}

i=1,…,8

(7)

令I={X1,X2,…,X8}，则I为设备制动优先情况下被测系统TSM的一个IECP。根据得到的I，分析设备制动优先方式下有限状态机的内部状态迁移和输出情况，结果见表5。

从表5可以看出A1～A2，但其余Ai两两之间都不满足I/O等价关系，所以在设备制动优先情况下，对于状态迁移系统描述的TSM状态机，最简化的I/O等价类应该为{q1=A1∪A2,q2=A3,q3=A4,q4=A5,q5=A6,q6=A7}。根据表5中数据，发现任何输入等价类Xi之间都不存在I/O等价关系。因此，目前得到的输入等价类划分I={X1,X2,…,X8}已是被测系统TSM需要的IECP。

3.3.4TSM故障模型

针对两种不同的制动优先情况考虑设定不同的故障域。设备制动优先情况下的故障域设为D(T，m=8，I)，司机制动优先情况下的故障域设为D(T，m=6，I)。其中，m表示与参考模型具有一致性(或非一致性)关系的所有故障域模型的等价类状态的数量上限，I为3.3.3节中构建的IECP。

表5 设备制动优先情况TSM有限状态机迁移及输出情况

假定设备制动优先条件下实际TSM曲线在测试中的内部状态迁移情况见图7。该故障模型满足给定故障域条件，并在参考模型的基础上增加了一个控制状态NORMAL_1。当SUT在OVERSPEED状态并且满足V≤VP时，状态机迁移到静态NORMAL_1。在此状态下，当满足V>VP+dV_EBI的条件时，进行唯一的输出迁移至目标状态EMER_BRAKE。但在这种情况下，SUT在进入NORMAL_1后，系统的报警和常用制动功能被屏蔽，仅能保证紧急制动的有效触发，这显然是有严重安全隐患的。此外，TSM状态机的等价类状态数量相较于参考模型增加了2个。基本状态NORMAL和OVERSPEED状态不再具备I/O等价关系，而NORMAL_1状态和其他任何基本状态都不具备等价关系。

3.3.5 生成完备测试集

结合TSM模型的迁移分析和对输入域的有限划分，在引入故障模型F=[T，～，D(T，m，I)]后，可根据W-Method分别生成两种制动情况下的测试用例集，使得该测试集对于所有系统行为等价于故障模型中某一元素的SUT都满足完备性要求。

(1) 设备制动优先情况

分析表5中有限状态机迁移和输出情况，以及参考模型T最简化的I/O等价类，我们可以容易地得到W-Method公式中的P和W。

其中,P={ε,ci,cj·ci|i=1,…,8,j=4,…,8}ci∈Xi，ε为空输入序列；W-Method表达式中的XI属于Xi。根据表6中的筛选情况，确定W={c3}，满足输入为c3时，对于不同的状态产生不同的输出序列。

表6 筛选后设备制动优先情况TSM有限状态机迁移及输出

设备制动优先情况下，最终的等价类状态数量n=6，确定故障域为D(T，m=8，I)。SUT满足可测试性假定，则最终希望生成的完备测试集为

{cicg|i=1,…,8,g=3}∪

{cickcg|i,k=1,…,8,g=3}∪

{cickclcg|i,k,l=1,…,8,g=3}∪

{cjcicg|i=1,…,8,j=4,…,8,g=3}∪

{cjcickcg|i,k=1,…,8,

j=4,…,8,g=3}∪

{cjcickclcg|i,k,l=1,…,8,

j=4,…,8,g=3}

(2) 司机制动优先情况

同理，根据表3中数据及参考模型T最终的I/O等价类状态，得到W-Method公式中的参数P′和W′。其中P′={ε,di,dj·di|i=1,…,8,j=6,7,8}di∈Xi，ε为空输入序列；W-Method表达式中的XI属于Xi；确定W′={d5}。

司机制动优先情况下，最终的等价类状态数量n=4，引入故障域为D(T，m=6，I)。SUT满足可测试假设时，在给定故障模型条件下，生成完备的测试用例集为

{didg|i=1,…,8,g=5}∪

{didkdg|i,k=1,…,8,g=5}∪

{didkdldg|i,k,l=1,…,8,g=5}∪

{djdidg|i=1,…,8,j=6,7,8,g=5}∪

{djdidkdg|i,k=1,…,8,

j=6,7,8,g=5}∪

{djdidkdldg|i,k,l=1,…,8,

j=6,7,8,g=5}

利用测试自动化工具RT-Tester[19]的RTT-MBT测试组件，针对TSM模型内部状态增加(故障域范围内)、状态减少和迁移错误3种不同的故障模型类别，进行自动测试用例的生成。分别就两种不同制动优先情况，对不同故障模型的测试效果进行了对比分析，见表7。

通过生成测试用例的数量、生成时间以及内存消耗来衡量测试用例生成方法的有效性。在满足相关测试要求的前提下，测试用例数量越多表明完成测试目标所需代价更大，测试用例生成的时间越短表明生成效率越高，内存消耗越少表明测试用例生成效率越高。对表7中数据分析表明：在确定某一控制优先级前提下，针对内部状态迁移错误的故障模型，测试用例生成时间和内存消耗最少，状态减少情况次之，状态增加情况的生成时间和内存消耗最多，效率更低；人控优先相对于机控优先，在确定故障模型时，前者生成的有效测试用例更少，所需资源也更少。

表7 不同制动优先情况下TSM测试用例比较

4 结束语

本文提出了一种针对CTCS-3列控系统TSM曲线完备性测试用例的生成方法。结合CTCS-3的SRS，建立了满足司机制动优先和设备制动优先两种不同制动优先级情况下的TSM有限状态机模型。利用I/O等价原理和等价类划分理论，得到了两种不同制动优先情况下的IECP，有效解决了参数输入域规模大的问题。同时，针对TSM曲线的故障模式复杂问题，引入故障模型，并确定了相应的故障域范围。在此基础上，利用W-method方法，在模型故障域约束内，最终得到两种不同制动优先的TSM曲线模型完备测试集。通过对生成测试用例的比较分析，表明了该方法的有效性。