基于交互式马尔可夫链的CTCS无线通信可靠性分析
2020-05-29谢雨飞田启川
谢雨飞, 田启川
(北京建筑大学 电气与信息工程学院,北京 100044)
CTCS是为了保证列车安全运行,并以分级形式满足不同线路运输需求的列车运行控制系统,包括车载子系统和地面子系统两个部分[1-2]。无线通信网络(GSM-R)在CTCS-3级和CTCS-4级列控系统中,用于车载子系统与列车控制中心之间的双向信息传输,它的可靠性与CTCS整个系统的可靠性和安全性紧密相关[3]。
目前,针对CTCS无线通信系统可靠性的分析方法主要有随机Petri网、着色Petri网、概率模型检验、连续时间马尔可夫链CTMC等[4-7]。这些方法的一般思路:根据CTCS无线通信中的各种随机故障情况抽象出系统模型,以状态转移或者随机概率刻画出系统动态特征,通过形式化验证工具和仿真的方法对模型进行分析和评价。比如,Amparo等[8]使用马尔可夫模型对瑞典铁路无线通信可靠性和安全性进行了评估和模拟,并量化了系统可靠性和安全性的概率;Holger[9]等利用STOCHARTS建立了ETCS无线通信的模型,确定了模型中的时间参数,并对无线通信的可靠性进行了定量分析;Kim等[10]建立了韩国铁路无线通信系统的分析平台,对无线通信的覆盖率、数据传输可靠性等进行定量测试;赵会兵等[11]采用SimEvents与Stateflow相结合的方式实现车地无线通信的建模与仿真,分析了安全连接建立时间和不同长度无线应用消息的传输延迟时间。然而,以上方法在建模与分析中都存在一些问题:一方面,CTCS无线通信中既存在确定行为的动作转移,又存在非确定行为的概率转移,而之前的性能分析中,面对这个问题时通常都是进行归一化处理,这往往并不容易实现,更为重要的是,归一化处理只是一种近似或抽象,与实际情况存在偏差[12-13];另一方面,CTCS无线通信中带有同步的并发操作在这些模型中并不能很好地表示出来[14]。
本文利用交互式马尔可夫链[15]对CTCS无线通信的可靠性进行建模与分析。该方法能够较好地解决以上两个问题,并且能够将标记转移系统中的动作转移与连续时间马尔可夫链的概率转移(马尔可夫转移)正交融合,与实际情况更加符合。由于交互式马尔可夫链结合了传统的进程代数模型和连续时间马尔可夫链模型的特征,因此非常适用于复杂系统的性能刻画与分析,在系统可靠性分析方面有广泛的应用,如文献[16-18]。另外,本文给出了基于交互式马尔可夫链的模型检验算法,分析了不同参数条件下CTCS无线通信的可靠性。
1 CTCS无线通信系统
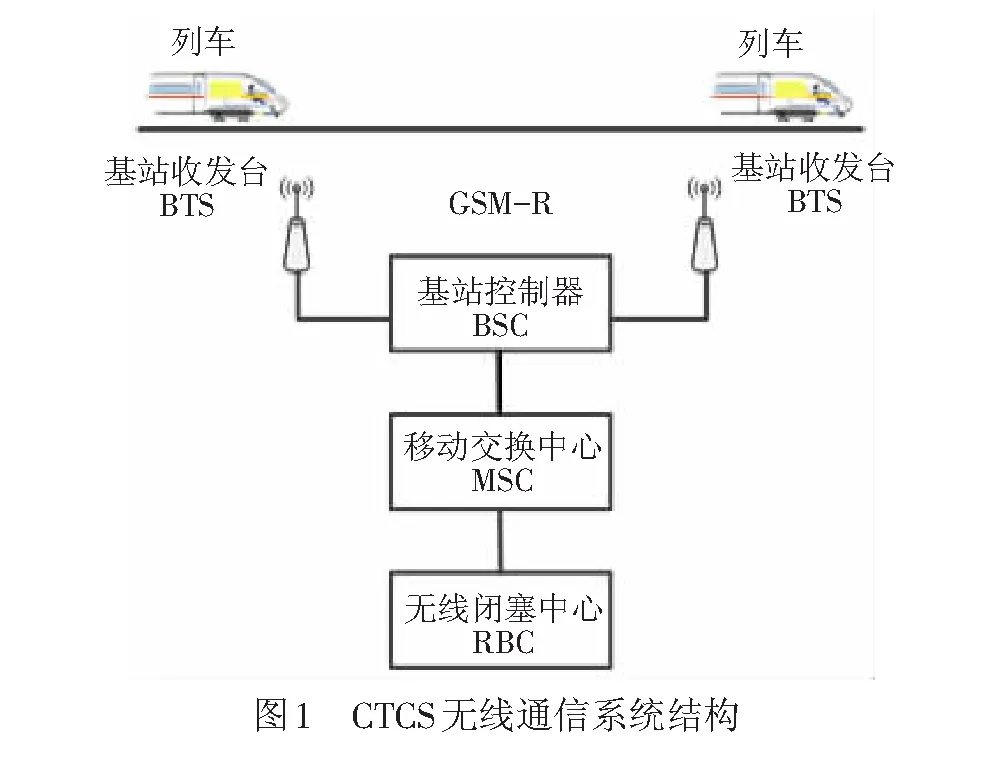
CTCS无线通信系统结构示意见图1,由基站收发台(Base Transceiver Station,BTS)、基站控制器(Base Station Controller,BSC)、移动交换中心(Mobile Switching Center,MSC)等几个部分构成。BTS完成通信网络和列车之间的通信和管理功能;BSC是基站子系统的控制和管理部分,负责完成无线网络管理、无线资源管理及无线基站的监视管理,控制移动台与BTS无线连接的建立、持续和拆除等管理;MSC完成网络中基本的交换功能,实现列车与无线闭塞中心(Radio Block Center,RBC)之间的通信连接。RBC是一个安全计算机系统,它根据来自外部信号系统(如联锁设备)的信息,以及与车载设备交换的列车位置和完整性报告,生成列车移动授权信息,以保证列车在无线闭塞中心的管辖范围内安全运行。
2 CTCS无线通信系统的交互式马尔可夫链模型
2.1 交互式马尔可夫链
一个交互式马尔可夫链为一个五元组(S,Act,→,…>,s0)[19]。其中,S为一个非空的状态集合;Act为动作集合;→⊆S×Act×S为动作转移关系;…>∈S×R0×S为概率转移关系,满足∀s1,s2∈S,|(…>∩({s1}×R0×{s2}))|≤1;s0为初始状态。在这里,动作转移与概率转移均得到保持。对于任何一对状态之间,最多存在一个概率转移关系。如果原始模型有多个概率转移,则需要将它们合并为一个,其转移概率为原来各个转移概率之和。
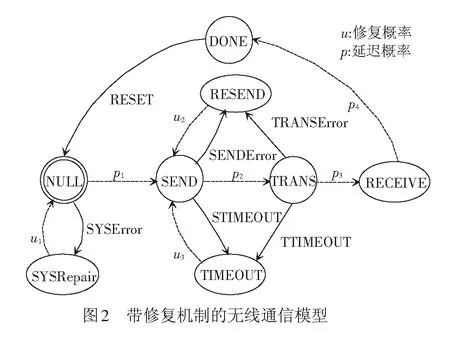
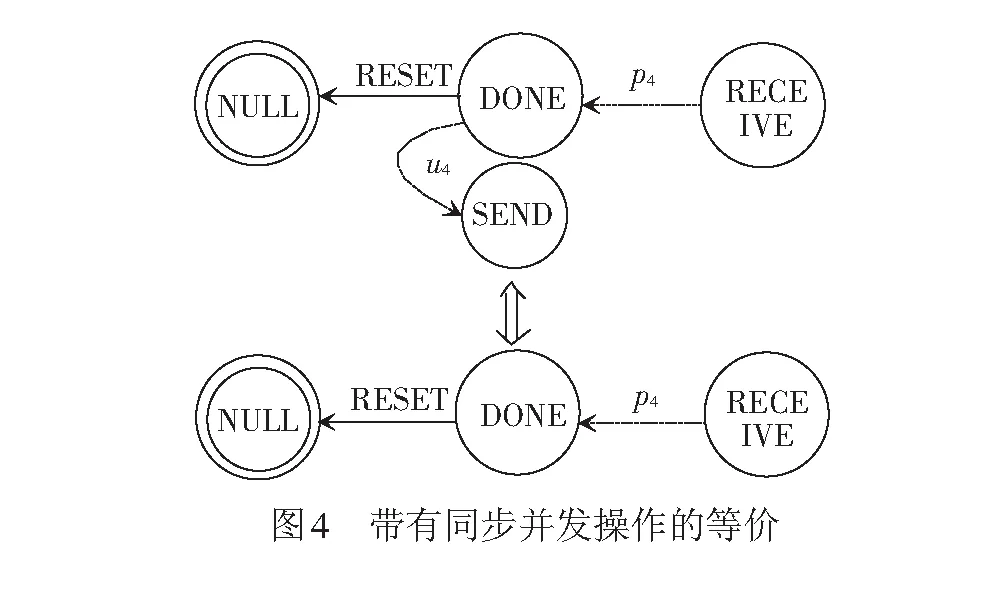
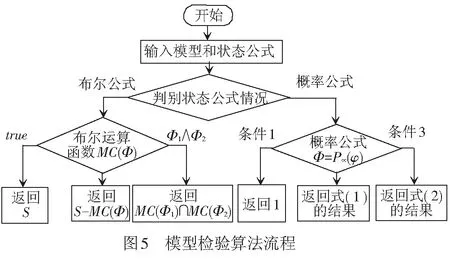
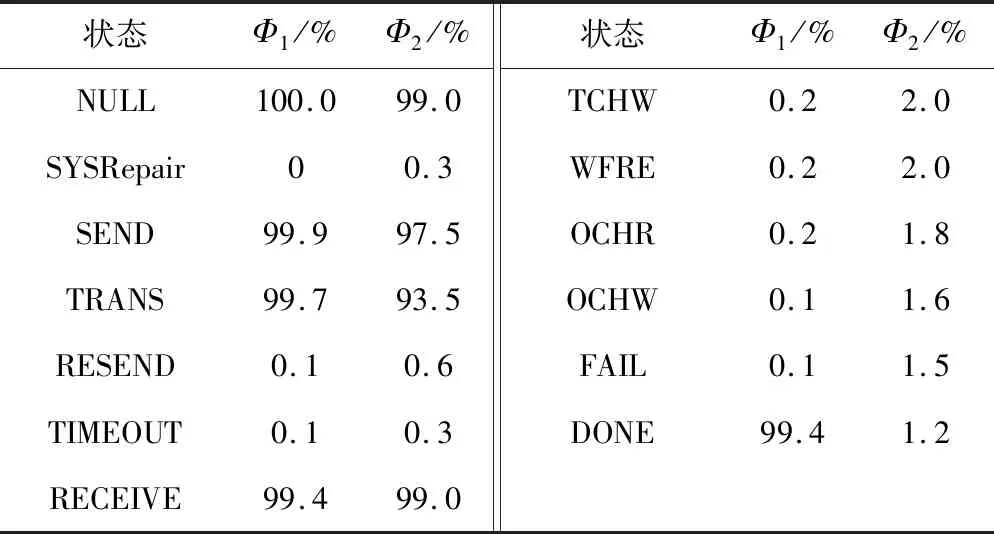
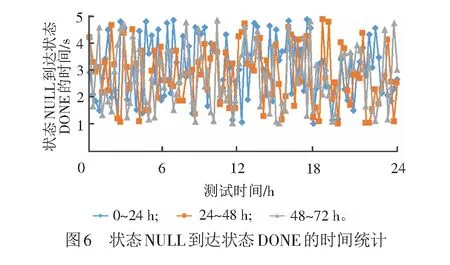
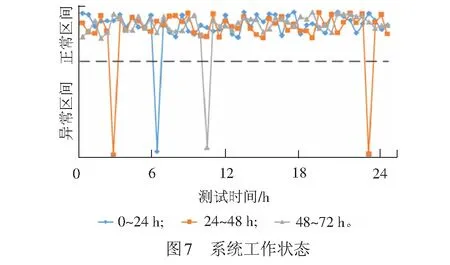
交互式马尔可夫链模型的逻辑可以用基于动作的时序逻辑来刻画,实际是在连续随机逻辑的基础上修改而来。其逻辑定义:设概率p∈[0,1],关系符号∝∈{<,≤,>,≥},基于动作的时序逻辑的状态公式Φ由以下语法产生,Φ::=true|Φ∧Φ|Φ|P∝(φ);对t∈R>0,A⊆Act,基于动作的时序逻辑的路径公式φ由以下语法产生,φ::=ΦAΦ。状态公式中的∧、分别为与和非,可以推导出其它所有命题逻辑连续关系;M/A=P‖RESETQ为满足路径公式φ的路径集合的概率测度在∝p所限定的范围内。路径公式中的算子U s|=true,对任意的s∈S; s|=Φ,当且仅当s|≠Φ; s|=Φ1∧Φ2,当且仅当s|=Φ1∧s|=Φ2; s|=P∝(φ),当且仅当Prob(s,φ)∝p。 在这里,Prob(s,φ)为Path(s)中所有满足路径公式φ的路径的概率测度。 设无线信道延迟概率为每小时pi(i∈{1,2,3,4})次,无线通信故障后系统的修复时间为1/uj(j∈{1,2,3})h,一个带修复机制的无线通信模型见图2。 系统的初始时刻为NULL,此时系统所有部件都是正常的。需要发送数据时,系统有两种可能: (1) 通信系统故障,执行动作SYSError后转移到状态SYSRepair;在状态SYSRepair时,若系统得以修复,以概率转移回初始状态NULL,停留时间满足参数为u1的指数分布。 (2) 在状态NULL停留一定时间系统仍然未发生动作SYSError,则概率转移至状态SEND,停留时间满足参数为p1的指数分布。 其余动作转移和概率转移与此原理相同,因此不再详细描述。模型中各状态和动作含义见表1。 表1 带修复机制的无线通信模型状态和动作含义 为了提高无线通信的可靠性,车地双向信息传输往往采用双网冗余的结构。有三种冗余需求等级:一般系统,系统恢复时间为200~500 ms;软实时系统,系统恢复时间小于200 ms;硬实时系统,系统恢复时间小于1 ms。 双网冗余结构无线通信模型见图3。设每个网络的故障率为λ,修复时间期望值为1/u,Fi(i∈{1,2})为i个正常工作网络中的其中一个出现故障,动作Repair表示网络的修复。系统必须保证至少一个网络正常才能工作,否则将进入瘫痪状态。模型中各状态和动作含义分别见表2、表3。 表2 双网冗余结构无线通信模型状态含义 表3 双网冗余结构无线通信模型动作含义 在图2和图3的模型中,无线通信系统的所有动作与信道延时、通信故障、网络故障等随机事件都是彼此分隔的,而且随机分布延迟不影响系统的动作转移操作,所以这是对标记转移系统的一种正交扩展。需要同步的动作的执行时间,发生在并发执行的所有组件都准备好执行该动作的时候,因此,同步的发生意味着该动作的所有延迟都已经完成。在模型中,动作RESET是需要同步的,记为‖RESET。设带修复机制的无线通信模型的主进程为P,双网冗余结构无线通信模型的主进程为Q,则带有同步的并发操作模型表示为Model=P‖RESETQ。 除了带有同步的并发操作外,模型Model中的其他动作都被看成内部动作,即外部将不再能够观察到。用符号ModelASET表示集合ASET中的动作为内部动作而被隐藏。在进行并发操作时采用的原则是内部动作的执行不允许时间延迟。也就是说,如果系统有内部动作要执行,则该动作应该立即执行。因此,当系统中的一个内部动作转移与概率转移共同存在于一个状态时,概率转移可以被忽略。比如,若RESET为系统内部动作,则当系统处于状态DONE时,图4的两个执行过程实际上是等价的。 通过这种方法,不仅保持了并发系统中的概率特征,也能够解决同步动作的随机分布问题。 针对以上模型,可以采用一种穷举算法进行模型检验,目标是判定模型是否满足所给的状态公式。算法的思路:遍历状态空间,找出所有满足给定功能和性能公式Φ的状态集合,判断该交互式马尔可夫链模型Model的初始状态s0是否在其状态集合中,从而决定Model是否满足公式Φ。 由于Φ::=true|Φ∧Φ|Φ|P∝(φ),可以由以下情况构建算法。 (1) 对于布尔公式,可以由Sat(Φ)的定义直接获得: 若Φ=true,Sat(true)=S; 若Φ=Φ1∧Φ2,Sat(Φ1∧Φ2)=Sat(Φ1)∩Sat(Φ2); 若Φ=Φ,Sat(Φ)=S-Sat(Φ)。 (2) 对于概率公式Φ=P∝(φ),需要考虑以下几种情况: ② 若s只存在概率转移,且s|=Φ1(条件2),则有 (1) 可以认为是在时间[0,t]内,从状态s转移到状态s′的概率。 ③ 若s既存在动作转移又存在概率转移,且 (s|=Φ1)∧(δAB(s)<δB(s) 则有 (2) 式中:I(s,s′)为从状态s转移到状态s′所执行的动作。 ④ 其他情况,有 算法的流程见图5。 算法的伪代码实现如下: //交互式马尔可夫链模型检验算法 Model Checking for IMC(M,Φ,S,A,B,t) //输入:模型M、状态公式Φ、状态集S、动作集A和B、时间约束t //输出:Bool functionProb(s,t)//定义概率测度函数 begin for alls∈S,x Prob(s,x)=0//赋初值 end for eachs∈S switch(s) //根据不同情况分别计算 case a:Prob(s,t)=1 end end functionMC(Φ)//定义布尔运算函数 begin switch(Φ)//根据布尔公式计算 casetrue:returnS caseΦ1∧Φ2:returnMC(Φ1)∩MC(Φ2) end end begin//算法的主流程 Sat(Φ)=MC(Φ) ifs0∈Sat(Φ) returnT else returnF end 我们在Intel i7处理器、16 GB内存、Windows 10操作系统的工作站上对模型进行了检验。模型中无线信道延迟概率参数依据实验设备参数获得,其余参数取系统长时间运行的平均值。 具体参数数值:无线信道延迟概率p1,p2,p3,p4分别为1×10-4,1×10-4,2×10-4,2×10-4。 网络的故障率为λ=1.0×10-4;修复时间期望值为u=2.0×10-5h。 现在验证系统以下两项的系统可靠性指标: (1) 系统在7 s内由状态NULL到达状态DONE的概率大于99%。 状态公式表示为 (2) 系统在24 h内连续正常工作的概率大于95%。 状态公式表示为 其中,第一项指标可以反映系统正常工作的能力,第二项指标可以反映系统连续工作的性能。 算法运行结果见表4。 表4 模型检验结果 可以看出,Sat(Φ1)={NULL,SEND,TRANS,RECEIVE,DONE },Sat(Φ2)={NULL,SEND,TRANS,RECEIVE }。可见,对于这两个性能指标,均有初始状态s0=NULL∈Sat(Φ1)和s0=NULL∈Sat(Φ2)。因此,如果系统从状态NULL开始运行,则系统在7 s内由状态NULL到达状态DONE的概率大于99%,且系统24 h连续正常工作的概率大于95%,满足要求。上述过程证明,该算法可以实现系统随机性能的检验。 为了检验算法的正确性,我们将仿真系统连续运行72 h,检测上述两项指标的实际值,并作统计处理,其实际结果见图6、图7。 在图6中,由状态NULL到达状态DONE的时间集中于区间1~5 s内,符合算法判定的概率特征。在图7中,连续24 h工作出现异常概率分别为2%、4%、2%,并且在出现异常情况时,系统均修复成功,与算法计算结果相符。 从测试结果可以看出,相比于Petri网、自动机、概率模型检验等方法,CTCS无线通信的交互式马尔可夫链模型及其模型检验算法具有以下优点: (1) 能够综合系统的动作转移和概率转移,实现系统可靠性的定量分析。比如列车或RBC通过无线通信系统发送信息时(状态SEND),数据能否按时到达目的节点、是否超时重发,均受无线信道延时影响,会呈现概率特性,这是非确定行为的概率转移。对于Petri网和自动机来说,这种行为无法描述。而在交互式马尔可夫链模型中,可以通过概率p2实现。如果出现异常,超时则执行动作TTIMEOUT,传输错误则执行动作TRANSError,这些都是确定行为的动作转移,对于概率模型检验来说,这些行为也无法直接描述。 (2) 上述交互式马尔可夫模型,在一定条件下与Petri网或概率模型检验模型具有相通性。仍以列车或RBC通过无线通信系统发送信息(状态SEND)为例,如果信道永远都是正常的,则模型中没有概率转移,这种情况下的交互式马尔可夫模型就是一个标记转移系统,它与Petri网模型刻画的内容是一致的,验证结果也是相同的;如果系统中的所有行为都具有概率特征,此时的交互式马尔可夫模型就是一个模型概率模型。 本文利用交互式马尔可夫链建模和分析了CTCS无线通信的可靠性,通过正交融合的形式,保留了CTCS无线通信系统中的动作转移和概率转移,模型检验算法证明了方法的可行性。 需要指出的是,本文给出的交互式马尔可夫模型及其模型检验算法,目前缺乏自动化验证工具的支持,这是与Petri网、自动机、概率模型检验等方法相比的一个不足之处。 另外,本文中算法的效率可以进一步提高,对于这种穷举算法,其计算开销等于NT,在这里,N为状态数量,T为路径长度。可以推断,对于状态空间较小的系统,该算法可以快速有效获得结果。然而,随着状态数量的增大,计算开销呈指数形式增长,可能会引起状态空间爆炸,因此,可以考虑在模型检验之前进行模型约简,以缓解该问题的产生。另外,在模型检验时,计算机截断误差对算法精度有一定的影响,特别是概率计算结果与所给指标非常接近时,可能难以判断其结论,在这种情况下可以减小步长,以获得更高的算法精度。2.2 带修复机制的无线通信模型

2.3 双网冗余结构无线通信模型


2.4 并发操作的实现
3 模型检验算法

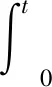
4 结果分析
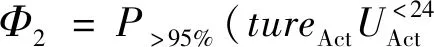
5 结论
