高速铁路路基压实参数对振动波演化特征的影响研究

叶阳升， 闫宏业， 蔡德钩，尧俊凯，陈 锋，耿 琳,2

(1.中国铁道科学研究院集团有限公司 高速铁路轨道技术国家重点实验室，北京 100081;2.北京铁科特种工程技术有限公司，北京 100081)

我国高速铁路自2003年开通第一条铁路后，进入快速发展阶段。截至2019年底，高速铁路里程达到了3.5万km，预计到2030年，高速铁路将实现内外互通互联的八纵八横高速铁路网宏伟蓝图[1]。随着高速铁路的发展，路基不再是简单的填筑碾压工程，其施工质量已经成为线路工程需要重视的薄弱环节[2]，这也对铁路路基的压实质量提出更高的要求[3-4]。

近年来，国内外专家、学者针对路基压实质量进行大量研究，路基的压实质量控制也从传统控制方法发展至连续压实控制技术，目前正在逐渐向路基智能压实技术发展，广泛采用压实计测值(Compaction Meter Value，CMV)作为压实质量的评判指标[5-7]。路基压实过程中振动波的传播演化机制是优化提升智能压实技术的前提。现阶段的研究成果主要集中在时域分析和频域分析，即从振动的时间、幅值及傅里叶谱等方面开展研究[8-9]。但是，振动波是一种复杂的非线性非平稳信号，其振动频率和振幅在压实过程中不断变化，单独从时域或频域开展分析将会对结果的精度产生不利影响[10]。目前，主要采用数值仿真和理论分析等手段开展研究，现场原型试验开展较少，有效的试验数据较少，进而大大限制了振动压实理论和智能压实技术的发展。

基于此，本文依托于京雄城际铁路固安东站段路基压实工程开展现场压实试验，从时域、频域、时频联合域及能量域四个方面，综合考虑振动压路机行驶速度、振动频率以及振动幅值的影响，系统研究振动压实过程中，振动波在水平方向的传播演化特征，以期为路基智能压实理论的发展提供支撑。

1 实验方案设计

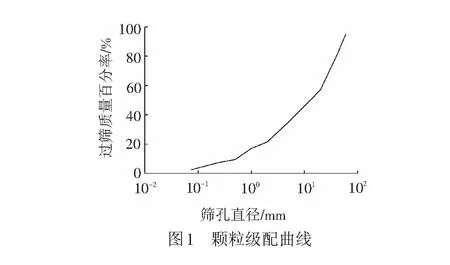
为研究不同压实参数下振动波的演化特征，在京雄城际铁路固安东站规划200 m×100 m(长度×宽度)试验场地。路基填筑高度为5 m，两侧斜坡的坡率为1∶1.75，填料为AB组角砾料，填料的级配见图1。

1.1 试验设备及其布置要求

本次试验采用振动压路机为三一重工SSR260C-6单钢轮压路机，振动压路机的工作质量为26.7 t，振动轮分配质量为17.1 t，驱动桥分配质量为9.6 t。振动压路机的振动频率分别为弱振和强振。振动频率为27～31 Hz，振动幅值为1.03～2.05 mm。振动轮的直径为1 700 mm，振动轮的宽度为2 170 mm，振动轮轮圈厚度为40 mm。加速度传感器采用东华的三向加速度传感器1C303，量程为±16.0g。

由于测试仪器的正确安装、埋设以及使用会对试验的精确性产生影响，因此要对传感器进行必要的防水和保护措施。在试验准备阶段，在传感器表面涂上一层酸性玻璃胶将其密封。由于三向加速度传感器对埋设方向具有较高的要求，本次试验在三向加速度计的底面粘贴了一块5 cm×5 cm×1 mm质量较轻、刚度较大的薄板，防止振动压实过程中加速度出现较大的转动。

1.2 测点布置情况

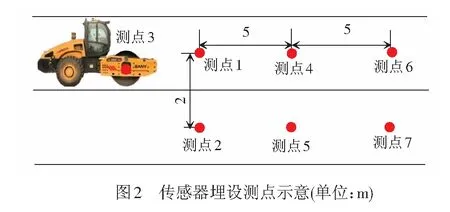
本次试验在工作车道和相邻车道填料中分别埋设了6个加速度传感器，在振动轮上布设了1个加速度传感器，传感器测点的埋设示意见图2。鉴于篇幅限制，本文选取了测点1、2、3开展研究。其中，测点1和测点2分别布设振动压路机工作车道和相邻车道填料，其埋深为5 cm，采集压实过程中工作车道和相邻车道的加速度相应；将无线加速度传感器安装于振动压路机的振动轮机架上，记为测点3，采集振动轮的加速度响应。数据采集设备采用东华测试32通道动态数据采集设备DH5922D，采集频率均大于2 000 Hz。

2 实验结果

为了研究振动波在传播过程中各参数对振动波演化特征的影响，以传感器为中心前后10 m范围进行压实试验，试验在3个试验区段分3次进行，每组试验进行两遍弱振一遍强振(一去一回为一遍)，重复3次。考虑到在路基压实过程中，振动压路机的行驶速度对填料压实度有一定的影响，鉴于现场智能无人驾驶压路机的行驶速度为3.0～4.0 km/h，本文选取行驶速度为3.0、3.5、4.0 km/h共3个工况进行试验。

2.1 加速度峰值传播规律及水平方向衰减率

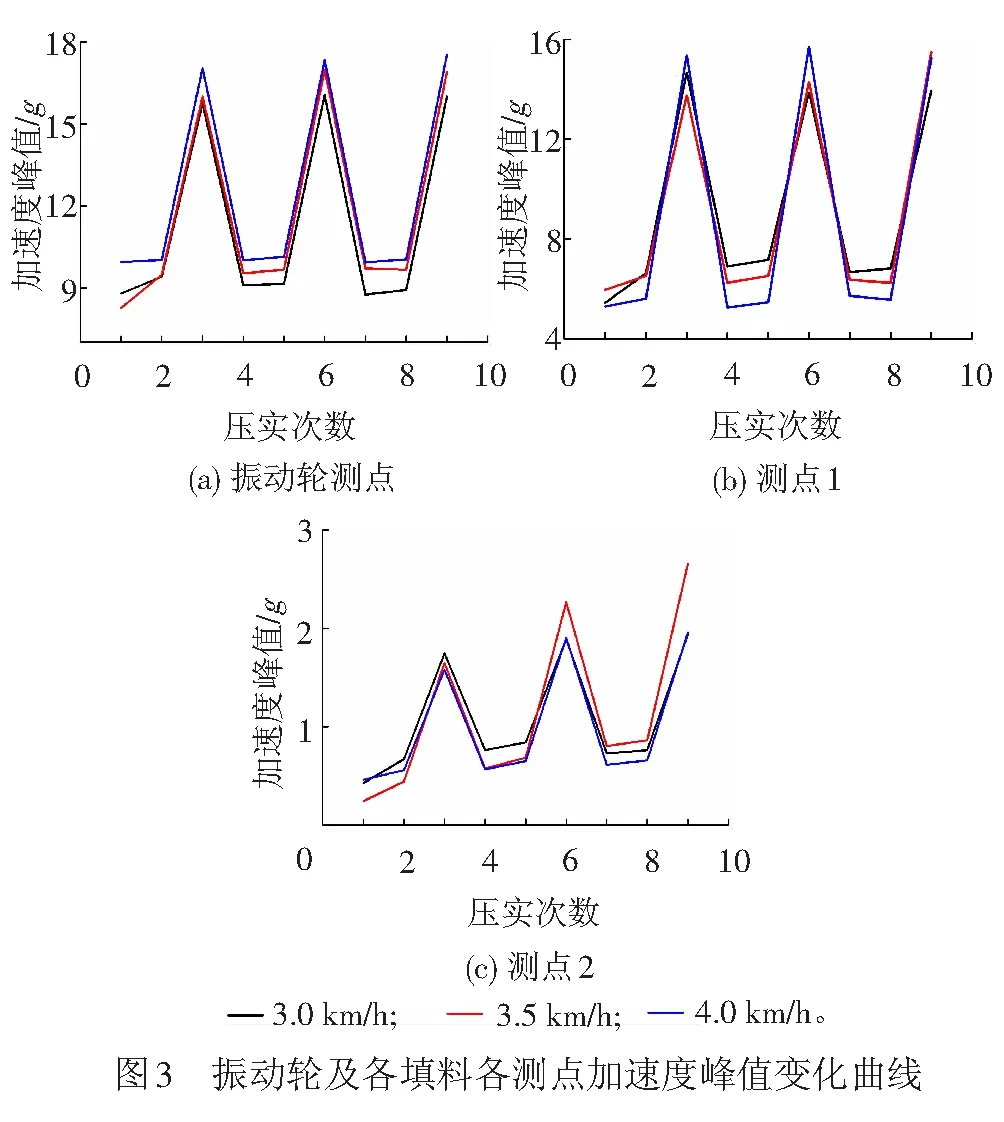
不同压实参数下，振动轮及填料各测点的加速度峰值变化曲线件图3。由图3可见，振动压路机强振压实时，振动轮及填料各测点的加速度峰值明显大于弱振，其加速度峰值约为弱振的两倍。随压实遍数的增加，各测点加速度大致呈现出增大的趋势。在不同行驶速度下，振动轮加速度峰值随着振动压路机行驶速度的提升而增大，而测点1的加速度峰值在弱振工况下随着行驶速度的提升而减小，在强振工况下则随着行驶速度的提升而增大；测点2在第一遍压实到第五遍压实时，行驶速度为3.0 km/h时加速度峰值最大，行驶速度为3.5、4.0 km/h时的加速度峰值大致相等。测点2在第五遍到第九遍压实时，行驶速度为3.5 km/h时加速度峰值最大，行驶速度为3.0 km/h时弱振加速度峰值略微大于4.0 km/h时的，强振加速度峰值大致相等。与振动轮和测点1相比，测点2加速度峰值受行驶速度影响并无明显规律。

为进一步说明振动波自振动轮到测点1再到测点2的传播过程，分别以振动轮与测点1之间的加速度峰值差值比上振动轮的加速度峰值为振动轮至测点1加速度峰值衰减率，同理表示测点1至测点2的衰减率，见图4。

由图4(a)可知，随着压实遍数的增加，在弱振工况下，行驶速度越快加速度峰值衰减率越低。而强振工况相反，其加速度峰值衰减率随行驶速度的增加而减小。对比强振工况和弱振工况来看，强振加速度峰值的衰减率远小于弱振的衰减率。由图4(b)可知，振动波自测点1至测点2水平传播过程中加速度峰值衰减率与行驶速度无明显关系，随着加压路机压实遍数的增加，加速度峰值衰减率有明显的下降趋势。

2.2 各测点加速度频谱特性分析

为研究不同行驶速度下，振动轮和测点1加速度时程曲线频谱特性的演化规律，将振动轮和测点1实测加速度进行快速傅里叶变换(Fast Fourier Transform，FFT)，得到基波和各次谐波的频率和幅值分布，见图5。

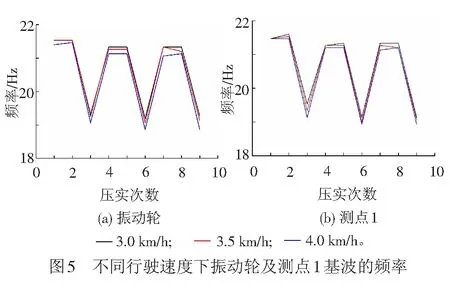
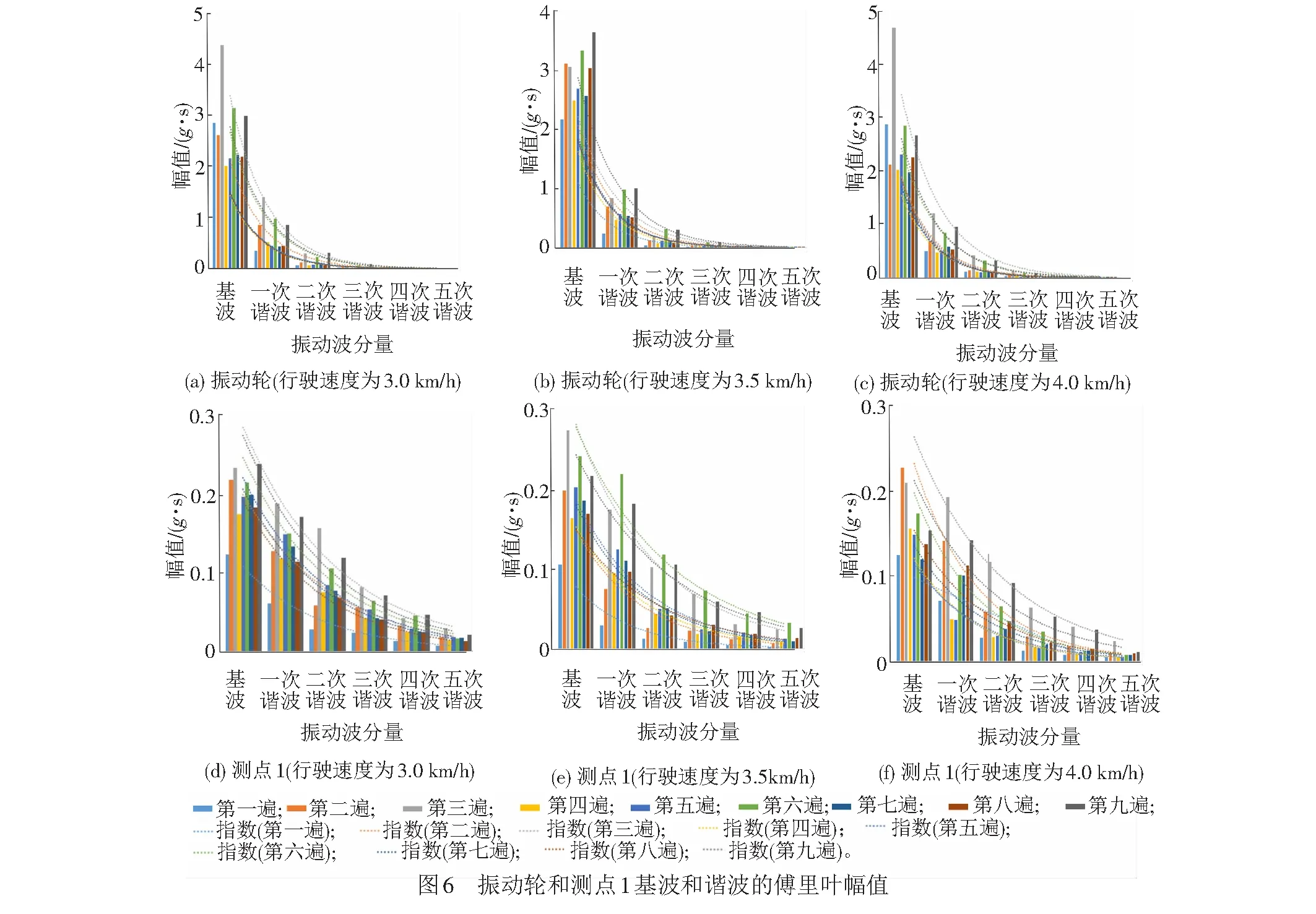
由图5可知，强振工况下的基波的频率小于弱振工况下基波的频率。随着行驶速度的增加测点1和振动轮呈现相同的规律，即振动压路机的行驶速度越快振动轮和测点1基波的频率越小。随着振动压路机压实遍数的增加，振动轮和测点1的基波的频率逐渐降低，整体呈下降趋势。

振动压路机在不同压实遍数、不同行驶速度下，振动轮和测点1基波和谐波的傅里叶幅值见图6。由图6可见，观察同一次振动的基波和谐波的傅里叶幅值，可以得出基波、一次至五次谐波的傅里叶幅值呈指数递减，且具有指数函数的相关性。指数函数的公式和相关性系数R2值见表1。

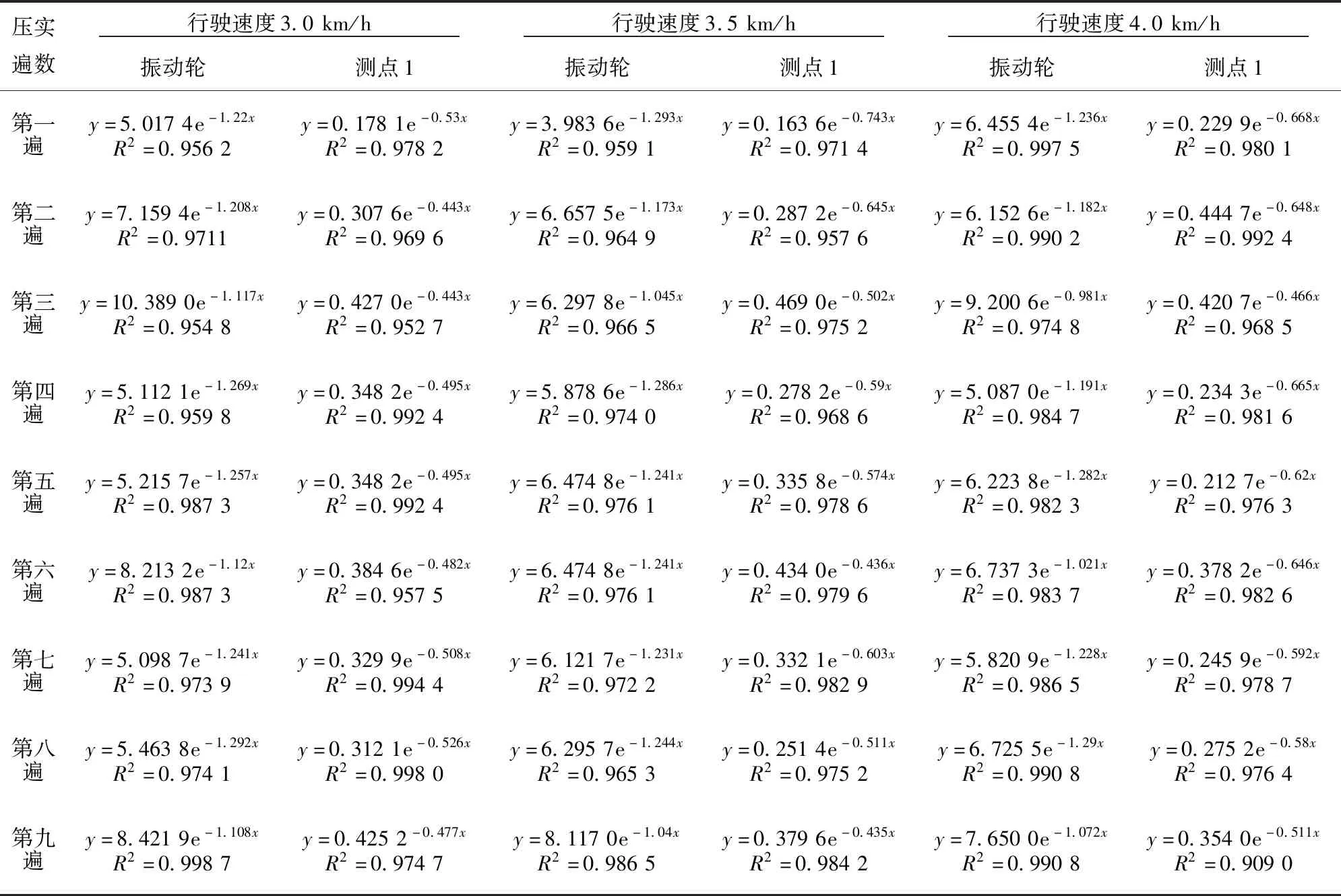
表1 指数函数的公式和相关性系数表

2.3 各测点Hilbert谱特性分析

为了表述振动波能量在不同压实参数下的演化特征律，本文基于加速度时程曲线，用Hilbert-Huang变换计算水平方向传播过程中的Hilbert-Huang谱。

2.3.1 Hilbert-Huang变换简介

Hilbert-Huang变换(HHT)理论，是一种适合分析非平稳时程的谱分析方法，由Huang变换和Hilbert谱分析两部分组成[11]。

基本步骤：

Step1利用EMD方法将给定的信号分解为若干固有的模态函数(Intrinsic Mode Function，IMF)，也称作本征模态函数，这些IMF是满足一定条件的分量。

Step2对每一个IMF进行Hilbert变换，得到相应的Hilbert谱，即将每个IMF表示在联合的时频域中。

Step3汇总所有IMF的Hilbert谱，得到原始信号的Hilbert谱[12-15]。

2.3.2 振动波的EMD分解和Hilbert谱

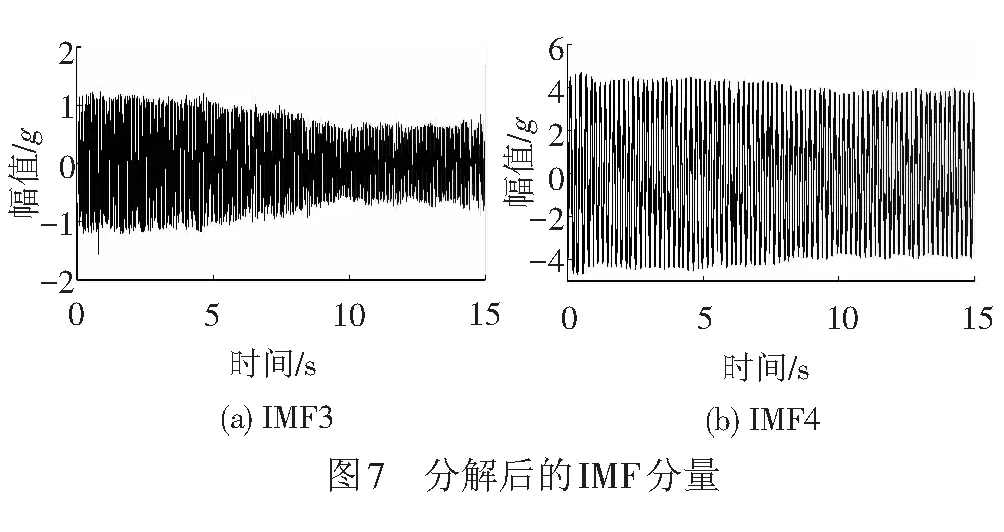
本文以振动压路机行驶速度为3.0 km/h时第一遍压实的加速度原始信号为例，将其进行EMD经验模态分解，得到12个IMF分量。对各IMF分量进行HHT变换，使用Matlab绘制其Hilbert能量谱，并以颜色的暖冷表示能量的大小。

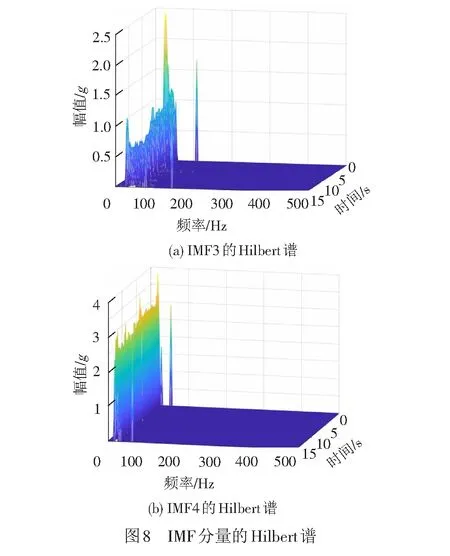
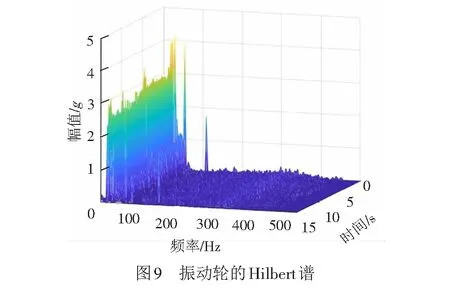
由图7可见，IMF4分量的幅值最大，且其波形图与振动轮原始波形图相似，其次为IMF3，其余分量幅值较小。由图8可见，MF4分量能量峰值最大，主要分布在与基波对应的频率附近；IMF3分量能量大小次之，分布在与一次谐波对应的频率附近。其余分量频率分布较广且峰值低的原因，可能是振动轮本身的干扰或者是试验过程中外界环境对其干扰。将每个IMF分量的Hilbert谱进行叠加，得到振动轮加速度的Hilbert谱，见图9。由图9可见，振动波的能量主要分布在低频部分，其频率和基波、一次谐波的频率所对应。

2.3.3 各测点边际谱演化规律

为进一步解释振动压路机在压实过程中振动波能量的演化特征，将Hilbert谱进行时间积分，得到信号在频率-幅值尺度上的分布规律，即为对应的边际谱的形式为

(1)

式中：H(ω,t)为Hilbert谱函数；h(ω,t)为Hilbert边际谱函数。

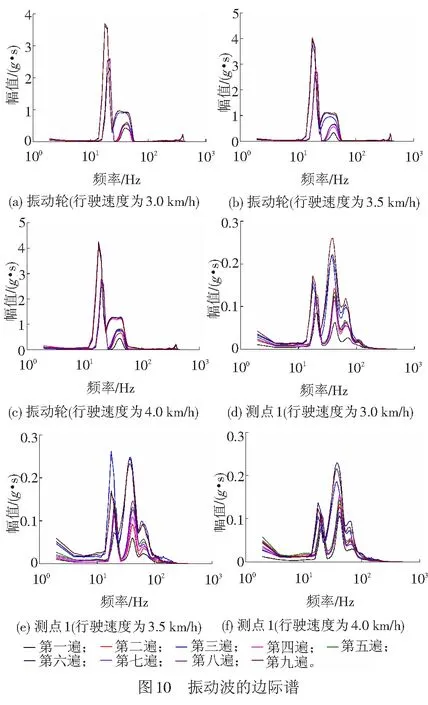
振动轮和测点1的边际谱见图10。从图10中可以明显看处，振动轮的边际谱为双峰值曲线，测点1边际谱为三峰值曲线。出现此现象的原因可能是随着振动波在填料的谐波对填料的影响很大。振动轮、测点1的边际谱的频率大多集中在10～100 Hz间，振动轮的能量集中于25 Hz，其中第三次压实、第六次压实和第九次压实为强振，其余六次压实为弱振，振动轮、测点1上强振的能量总是大于弱振的能量。由图10可知，振动轮、测点1上的能量随着压实遍数的增加而增加；振动轮的能量随着行驶速度的提升而增加，测点1随着行驶速度的提升而降低。测点1埋置于填料之中，其频率相比于振动轮的频率分布范围较广，且高频波能量峰值较低。振动波从振动轮→填料测点过程中的能量最大值所对应的频率有所改变，振动轮上能量峰值所对应的频率较低，测点一的能量峰值所对应的频率与基波频率相似。

3 结论

本文以京雄城际铁路固安东站路基压实工程为试验场地，从时间、频率和能量之间的相互关系研究了振动压路机在不同参数下的振动波传播规律，得出以下结论：

(1) 振动压路在工作过程中，压路机的行驶速度越快则填料的加速度峰值就越小，振动轮的加速度峰值就越大。随着振动压路机行驶速度的增加，由振动轮到填料传播过程中的加速度衰减率逐渐增加，振动波在填料中沿水平方向传播的加速度峰值衰减率随着压实遍数的增加而逐渐降低。

(2) 基于傅里叶变换，振动波在振动轮和填料中随着振动压路机的行驶速度增加呈现相同的规律，即随着压路机的行驶速度加快，振动轮和填料所对应的基波的幅值降低。振动压路机在不同速度行驶下，振动轮和填料振动波的基波和一次谐波到五次谐波幅值呈指数分布，且有严格的指数函数相关性。

(3) 在振动压路机工作过程中，对振动波原始信号进行Hilbert-Huang变换，得到不同速度下的边际谱。振动波在振动轮中的能量集中于25 Hz附近，振动波在填料中的能量集中于50 Hz附近。从边际谱来看，振动波在传播过程中，振动波能量峰值的频率增加，且随着压实遍数的增加，振动轮和填料的能量峰值逐渐增加，随着振动压路机的速度加快，振动轮和填料的能量峰值逐渐降低。