高铁环境下基于QoS用户业务的公平性功率分配算法

李翠然， 杜欣怡， 谢健骊

(兰州交通大学 电子与信息工程学院，甘肃 兰州 730070)

在高速铁路(High Speed Railways,HSRs)环境中，列车具有高移动性且列车与基站(eNB)之间的无线信道状态变化剧烈，同时大多数列车是运行在缺乏散射体的平原地区的高架桥上，在大尺度衰落环境下，往往会出现语音通话中断、切换、频繁掉话和丢包率严重等问题，极大地影响了用户的服务质量(Quality of Service,QoS)[1]。在多用户多业务传输模型中，合适的功率分配算法是使信道容量达到最大的必要条件。不同的功率分配算法适用于不同应用场景，因此，针对HSRs环境进行功率分配算法研究，对提升高铁用户体验(Quality of Experience,QoE)是十分必要的。

文献[2]提出了在满足用户中断概率的约束条件下，最大化系统容量的功率分配算法。文献[3-4]研究了总功率约束条件下，在不同场景提高系统吞吐量的功率分配算法。文献[5]在保证用户公平性和最低速率的前提下，提出了一种复杂度较低的比例公平资源分配算法。虽然上述算法系统性能及资源利用率有所提升，但忽略了用户自身QoS满意度需求。文献[6]以最小化平均消耗功率为优化目标，提出了一种具有QoS保障的用户调度和功率分配机制。文献[7]为了满足用户的多种需求，将网络容量和功耗效率构建成一个多目标优化问题，得到了适合不同用户需求的最优解集。文献[8]从用户满意度出发，针对不同场景用户对无线资源需求的不同，提出了基于QoE的无线资源调度优化算法。

综上所述，已有功率分配算法主要以提高频谱利用率、系统吞吐量和保证单一业务的QoS为主要研究目标。它们并未兼顾考虑HSRs场景下多业务用户自身的QoS满意度和用户间的公平性，因此无法确保高铁用户的实际传输速率能够达到该用户的期望速率。本文从提升高铁用户对QoS感知性能方面出发，基于不同类型信息流的最大耐受时延，将用户业务分为时延敏感业务和时延非敏感业务，并根据eNB能否预先获知用户的期望速率，分别采用基于用户期望和基于预分配的功率分配策略，使每个用户按其期望速率进行数据传输，不仅可以保证单个用户的QoS需求，而且最大化用户间的公平性，有效地降低了eNB发射功率，节约了网络资源。

1 系统模型

HSRs场景中，eNB等间隔地部署于铁路沿线[9]。为避免由于金属制品造成的穿透损耗和相邻小区间的组间切换，可以采用两跳中继协作的信息传输方式[10]，见图1。图1中，列车上的用户通过无线接入点(Access Point,AP)与eNB进行通信，AP通常安装于列车顶部，利用WiFi等技术即可实现AP和用户间的高速信息通信。因此，两跳中继协作传输系统的技术瓶颈是eNB和AP之间的信息传输，这正是本文研究重点。

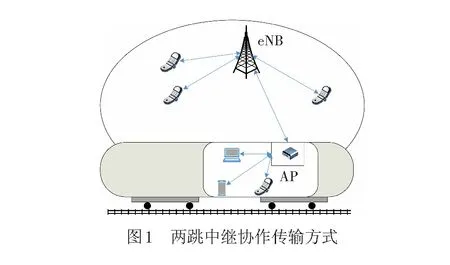
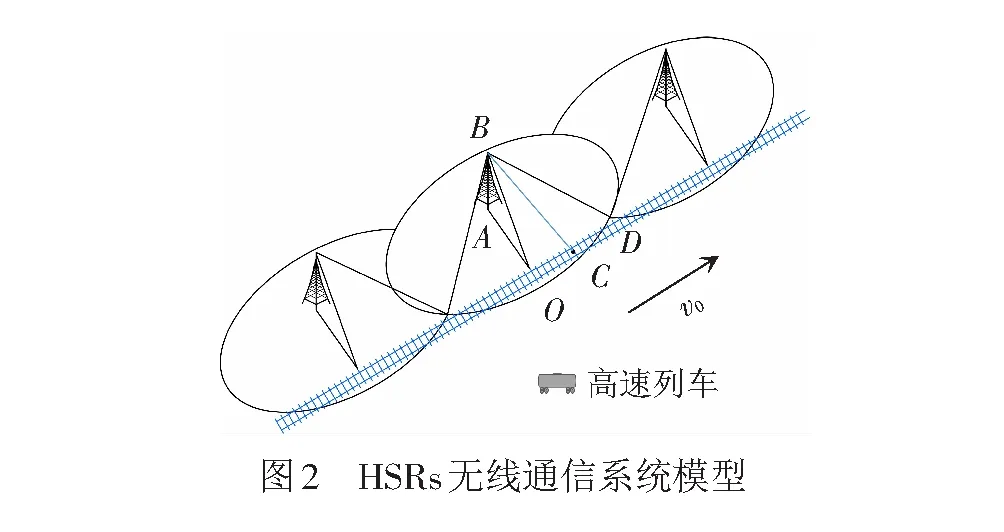
假设高速列车以恒定速度v0沿着铁路轨道行驶，且AP为单天线配置，则列车可被视为铁路线上的移动质点，eNB和AP之间的信息传输可视为点对点通信[11]。典型的HSRs无线通信系统模型见图2[9，12]。令eNB和铁轨之间的距离为d0，eNB天线高度为h0，eNB沿铁路沿线的覆盖半径为L，列车经过点O的系统时间被设定为0时刻，则列车在一个eNB覆盖区内的运行时间t的取值范围为[-L/v0，L/v0]，列车的实时位置为v0t，eNB和AP之间的传输距离d(t)可写为

(1)

在eNB和AP之间的点对点通信中，令x(t)和y(t)分别为t时刻的输入信号和输出信号。通常地，假设x(t)为均值为0、方差为1的函数，则y(t)可写为[12]

(2)

由此得到eNB在时刻t的瞬时信息传输速率

(3)

式中：B为系统的可用频谱带宽。

2 HSRs环境下的QoS业务

通常地，来自不同用户或应用程序的信息流有不同的QoS要求，如数据速率、最大耐受时延和时延冲突概率等。在两跳中继协作系统中，eNB经由AP与乘客进行通信，eNB传输的是来自列车上不同乘客的混合信息，即一组包含不同QoS要求的信息流。假设一个eNB覆盖区内的用户数目为N，用户期望速率和最大耐受时延向量分别为Rq=(R1，R2，…，RN)和τ=(τ1，τ2，…，τN)[12]。对于第i个信息流(i=1，2，… ，N)，若τi≥2L/v0(即列车在一个eNB覆盖区内的运行周期)，可将它看作时延非敏感信息，因为一个操作周期足够完成传输且不会产生时延冲突。相反地，若τi<2L/v0，则将该信息流视为时延敏感信息，需要实时传输以避免时延冲突。由此可知，基于用户信息流的不同传输延迟要求，可将信息流分为2类，时延敏感信息流和时延非敏感信息流，它们的数据传输速率Rds和Rdi分别为

(4)

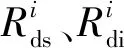
通常地，香农容量是在确定性信道条件下得到的信道容量。实际上，信道状态是一个不断变化的随机过程，应采用统计意义上的信道容量来描述，即中断容量和遍历容量。

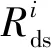
(5)

由式(3)得到时延敏感用户i的最大信息传输速率为

(6)

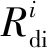
(7)

根据式(3)得到时延非敏感用户i的最大信息传输速率为

(8)

3 公平性功率分配算法

基于不同用户QoS的公平性功率分配算法，不仅要考虑每个用户的差异化业务传输映射的不同期望速率，同时要尽量保证多个用户占用无线信道的公平性。为体现用户满意度，定义单个用户的满意度因子αi为

(9)

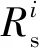
则用户间QoS业务的公平性可用差异化因子βij为

∀i,j∈(1，2，…,N)

(10)

βij越小，则说明用户间的公平性越好。

本文研究的公平性功率分配算法，是在eNB平均发射功率P0受限的条件下，使N个用户满足各自的QoS需求(最大耐受时延映射的期望速率)，并且使用户间具有较好的公平性。其目标函数为

(11)

约束条件为

s.t.

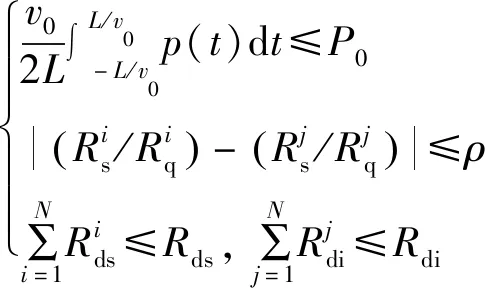
(12)

式中：ρ为预设的公平性指标阈值。

由式(3)可知，用户的传输速率与发射功率成正比。功率分配算法就是将eNB发射功率按照用户QoS需求(期望速率)进行按需分配。根据eNB能否预先获知用户的期望速率，分别采用基于用户期望和基于预分配的功率分配策略。

3.1 基于用户期望的功率分配策略(算法1)

算法1步骤为：

Step1根据不同时延用户要求的不同期望速率占总速率的比值，按比例分配eNB发射功率，即

(13)

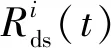
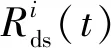
Step3令pi(t+1)=pi(t)·(1+Δp)，根据Romberg算法[14]，它是一种加速计算方法，在等距基点情况下，通过把区间逐次分半的方法进行加速。定义初始区间[a，b]，其中，a=0.01，b=0.1，步长为

(14)

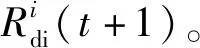
Step4转入Step2进行判定，直到满足约束条件或达到迭代次数为止。

3.2 基于预分配的功率分配策略(算法2)

算法2步骤为：

Step1首先，根据用户数目平均分配eNB的发射功率，即

pi(t)=P0/N

(15)

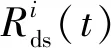
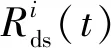
Step4转入Step2进行判定，直到满足约束条件或达到循环迭代次数时结束。

4 仿真结果

假设用户数目N=120，其中，60个时延非敏感用户和60个时延敏感用户。令时延非敏感用户和时延敏感用户的期望速率各分为3个QoS等级，分别为0.5、0.6、0.7 Mbit/s和1.0、1.1、1.2 Mbit/s。算法仿真参数见表1。仿真过程考虑了3类不同QoS等级的时延非敏感用户(用户1、2、3)和3类不同QoS等级的时延敏感用户(用户4、5、6)。

表1 仿真参数[12]

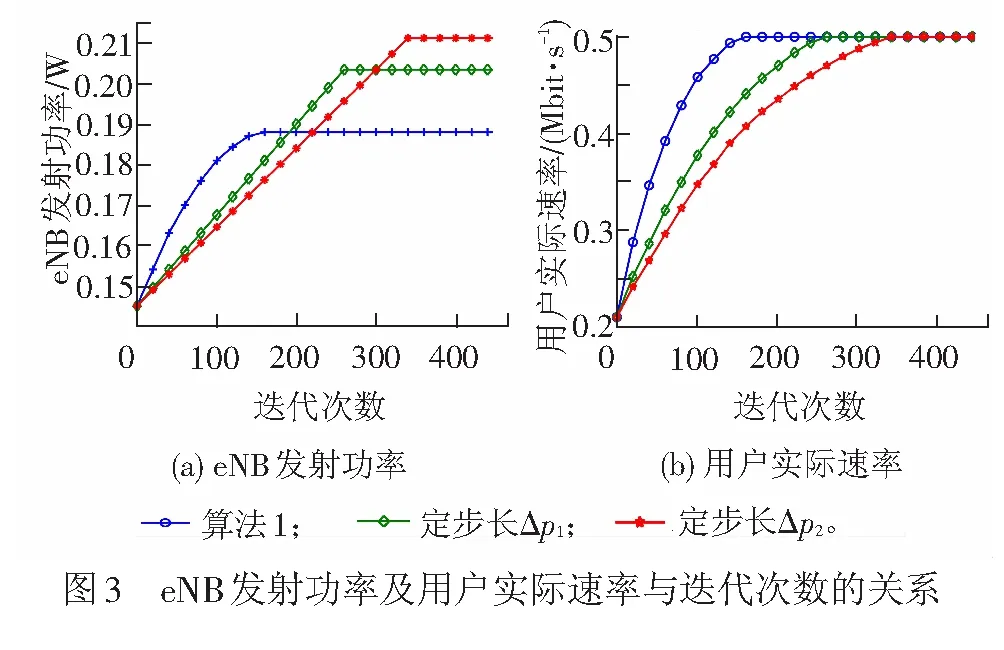
以用户1为例，将本文提出的算法与定步长算法进行性能比较，其中，定步长算法中的步长取值必须以满足公平性指标阈值为前提，仿真中分别为Δp1=0.045，Δp2=0.025。eNB发射功率与实际速度迭代次数的关系见图3。由图3(a)可知，对于定步长算法，步长越小(Δp2<Δp1)，达到用户期望速率的迭代次数越多，而文中算法1具有较优的收敛性能。由图3(b)可知，与定步长算法相比，当用户实际传输速率相同时，文中算法1具有较少的迭代次数和较低的发射功率。较优的算法收敛性能则说明eNB能快速地为用户提供相应的期望速率。

采用文中2种功率分配算法时，用户1—用户6达到各自期望速率的迭代次数见表2。

表2 达到用户期望速率的迭代次数

时延非敏感用户和时延敏感用户在相同传输速率下的收敛性能见图4。由图4可知，算法1和算法2均能以较少的迭代次数满足各类用户(6类QoS等级)的数据传输。

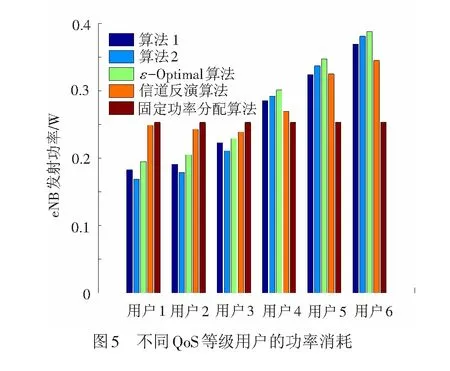
当列车在eNB覆盖范围边界时(t=-L/v0=-5 s)，6类不同QoS等级用户的功率消耗(eNB发射功率)见图5。将本文所提算法与固定功率分配算法、ε-Optimal比例公平算法和信道反演算法[11]在相同条件下进行对比说明。在eNB平均发射功率限定的条件下，5种算法均需满足用户期望速率所对应的最小发射功率。对比提出的2种功率分配算法，可看出：① 时延非敏感用户所需的功率消耗低于时延敏感用户，这是因为时延非敏感用户的期望速率较低；② 对于时延非敏感用户，算法2具有较低的功率消耗；③ 对于时延敏感用户，算法1的功率消耗较低。ε-Optimal比例公平算法的eNB发射功率高于本文所提2种算法；信道反演算法仅适合于时延敏感用户，对于时延非敏感用户会消耗较多的发射功率；固定功率分配算法无法满足时延敏感用户最小发射功率阈值，故既无法满足用户间公平性也无法达到用户QoS需求。

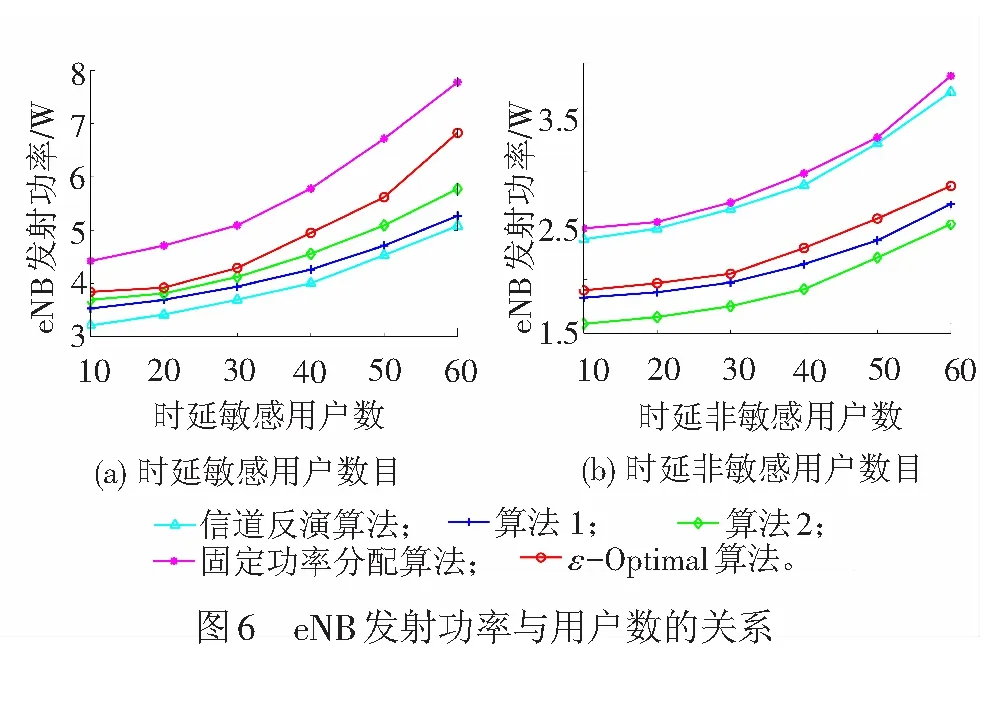
满足用户期望速率1.2、0.5 Mbit/s时，所需eNB最低发射功率与用户数目之间的关系见图6。由图6(a)可看出，随着时延敏感用户(1.2 Mbit/s期望速率)数目的增加，算法所需的eNB发射功率随之增加。对于时延敏感用户(1.2 Mbit/s期望速率)，算法1是基于用户期望按比例分配发射功率，对于高期望速率用户分配更多功率，相比于算法2根据用户数目平均分配发射功率能更快收敛到其期望速率，具有较低的功率消耗。由图6(b)可看出，随着时延非敏感用户(0.5 Mbit/s期望速率)数目的增加，算法所需的eNB发射功率随之增加。对于时延非敏感用户(0.5 Mbit/s期望速率)，算法2是根据用户数目平均分配发射功率，对于低速率用户分配更多功率，相比于算法1能更快收敛到用户期望速率，具有较低的功率消耗。对比图6(a)和图6(b)可知，具有较低期望速度的时延非敏感用户所需的eNB发射功率远低于时延敏感用户，且本文所提2种算法的功率消耗水平均低于ε-Optimal比例公平算法和固定功率分配算法。对于时延敏感用户，信道反演算法所需的eNB发射功率最低；而对于时延非敏感用户，文中算法具有最低的eNB功率消耗。

所提算法的单个用户满意度因子αi和用户间QoS业务的最大差异化因子max{βij}值分别见表3、表4。由表3可看出，所提2种算法对于6类不同QoS等级用户，其中αi值均大于0.99，说明它们具有较高的用户满意度；而ε-Optimal比例公平算法用户满意度低于本文所提2种算法；信道反演算法，仅能够满足时延敏感用户(用户4、5、6)QoS，却无法较好地满足时延非敏感用户(用户1、2、3)QoS；固定功率分配算法仅能够满足时延非敏感用户QoS，却无法较好地满足时延敏感用户QoS。由表4可知，所提2种算法对于6类不同QoS等级用户，其max{βij}值均小于公平性指标阈值ρ(ρ=0.005)，较好地保证了用户间公平性；而ε-Optimal比例公平算法虽然具有较低的max{βij}值，但结合表3用户满意度较低来说，本文算法更具优势；信道反演算法和固定功率分配算法都具有较高的max{βij}值，无法保证用户间的公平性。对比表3、表4可知，对于单个用户的满意度而言，算法2优于算法1；而对于用户间的公平性而言，算法1优于算法2。在实际的列车运行环境中，应折中考虑单个用户的满意度和用户间的公平性这两个指标，以选择合适的功率分配策略。

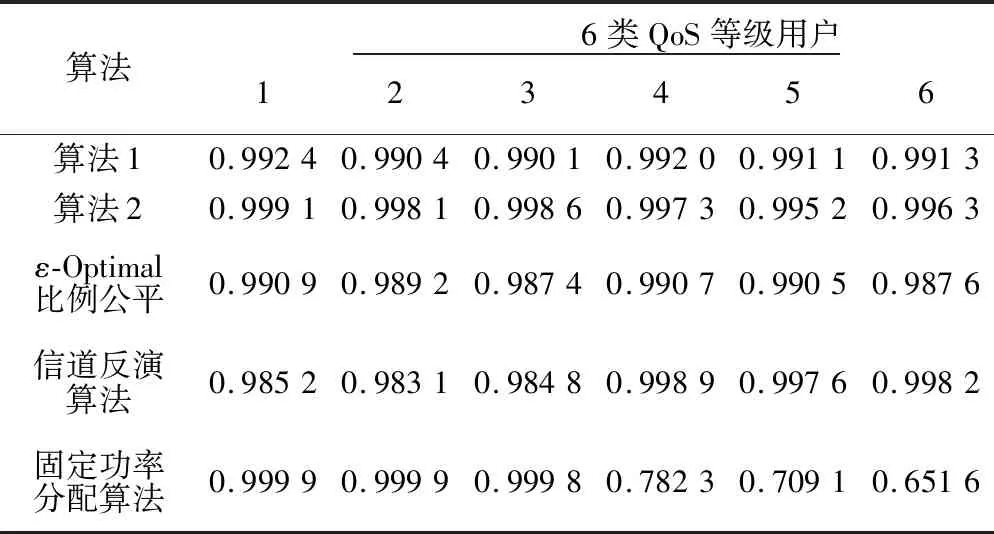
表3 归一化用户满意度因子αi

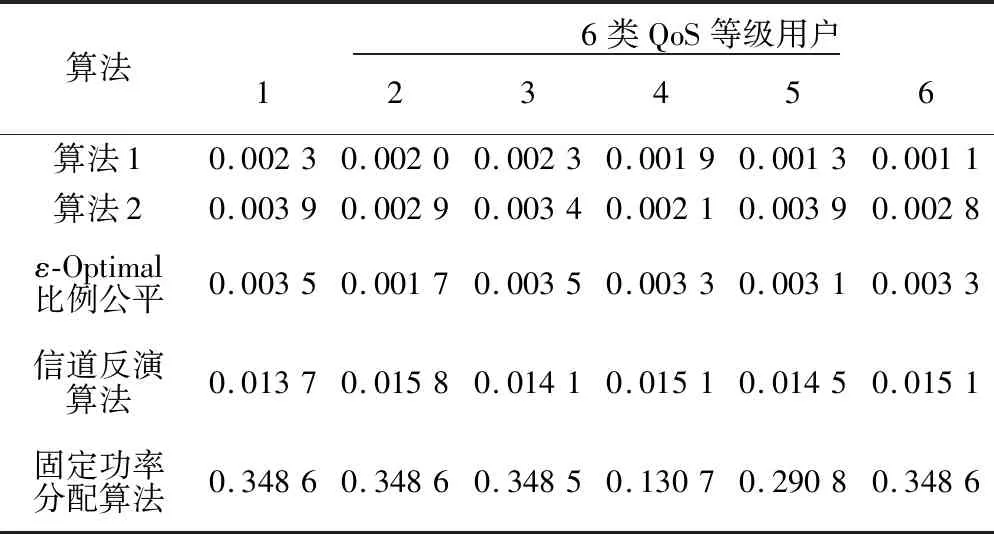
表4 用户间QoS业务的最大差异化因子max{βij}

5 结束语

本文针对HSRs环境，采用两跳中继协作的信息传输方式，根据点对点模型，得到eNB瞬时信息传输速率；并从满足不同列车用户QoS期望速率的公平性出发，研究了eNB平均发射功率约束条件下的功率分配问题。基于不同的时延要求，将用户分为时延敏感用户和时延非敏感用户；并根据eNB能否预先获知用户的期望速率，分别采用了基于用户期望和基于预分配的功率分配策略。仿真结果表明，所提2种算法均能获得优化目标的可行解，具有较高的单个用户满意度和用户间公平性。