深埋暗挖地铁车站施工阶段钢管柱承载力计算方法探讨

李明磊

（中铁第六勘察设计院集团有限公司，天津 300308）

1 研究背景

随着经济的发展，全国越来越多的城市开始修建地铁。在城市繁忙地带修建地铁车站时，往往占用道路，影响交通。当地铁车站设在主干道上，而交通不能中断，且需要确保一定交通流量时，为了尽可能减少对地面交通以及周边环境的影响，可采用暗挖洞桩法进行施工。

洞桩法就是将传统的盖挖法和暗挖法进行结合，即在地面上不具备施作基坑围护结构条件时，在地下施工导洞内施作边桩、中桩、中柱、顶梁、顶拱结构，形成桩、梁、拱及中柱支撑框架体系，承受施工过程的外部荷载，然后在顶拱保护下，逐层向下开挖土体，施作中楼板、底板及侧墙结构。

随着现在地铁埋深逐渐加大，层数逐渐增多，钢管柱越来越长，其施工阶段的承载力，按现有的计算公式很难满足承载力要求，文章在洞桩法施工阶段不加大钢管柱尺寸的情况下，就如何提高钢管柱承载力及如何更合理地计算其承载力进行探讨。

2 传统钢管柱承载力计算方法

文章以北京某地铁车站为例，来探讨承载力计算方法。

2.1 工程概况

车站为暗挖洞桩法施工三层车站，结构型式为双柱三跨拱顶直墙结构，车站拱顶覆土8.2m，底板埋深32.7m，钢管混凝土柱采用直径0.8m，壁厚16mm，钢材为Q235B，柱内填充C50 微膨胀混凝土，钢管柱长21.5m，各层长度分别为5.2m、6.7m、9.6m，钢管柱沿车站纵向间距7m。

2.2 钢管柱承载力计算

钢管柱施工完毕，顶部二衬扣拱完成后，钢管柱承受上部土压力及结构自重，而此时，钢管柱的计算长度最长，为最不利荷载，如图1 所示。

根据《钢管混凝土结构技术规范》（GB 50936-2014）计算[1]，初始条件：受轴压力：N施工=13010kN，N使用=14240kN；柱端弯矩：M施工1=M施工2=98kN·m，M使用1=M使用2=125kN·m；套箍指标：θ=Asf/（Acfc）=0.792；混凝土等级系数：α=2.00；轴心受压短柱的承载力设计值：N0=0.9fcAc（1+αθ）=24881.8kN。

（1）施工阶段考虑为轴心受压柱时的承载力。等效计算长度按式（1）计算：

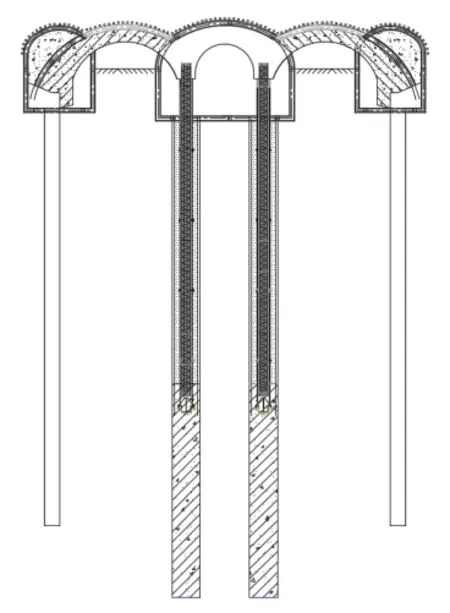
图1 施工步序：扣拱完成

式中：μ 为考虑柱端约束条件的长度系数，可按《钢结构设计规范》（GB 50017-2017）执行，本文取1[2]；l 为柱实际长度，m。

承载力折减系数按式（2）计算：

式中：D 为钢管柱直径，m。

按轴心受压柱考虑的承载力：Nu1=φ0N0=12018.6kN。

（2）施工阶段考虑为压弯柱时的承载力。两端弯矩较小值与较大值的比值β=1.000；等效长度系数k=0.5+0.3β+0.2β2=1.000；等效长度Le=kμl=21.500m；考虑长细比影响的承载力折减系数φl=1-0.0226（Le/D-4）=0.483；考虑偏心影响的承载力折减系数按式（3）计算：

式中：e0为柱端轴心压力之偏心距较大者，mm；rc为钢管内混凝土横截面半径，mm。

按压弯柱考虑的承载力：Nu2=φlφeN0=11597.7kN。

（3）使用阶段考虑为压弯柱时的承载力。由于受到纵梁约束，梁柱节点可按固定支座考虑，其等效计算长度L使用e=kμl=9.6m。

根据上述计算公式按压弯柱考虑的承载力按式（4）计算：

式中：φ使用l、φ使用e为使用阶段工况承载力折减系数，计算方法同φl、φe的计算方法。

2.3 存在问题

从上面计算可以看出：不论考虑钢管柱是轴心受压构件还是压弯构件，由于其计算长度达到21.5m，长细比影响因素非常大，其承载力都不满足承载要求；而使用阶段钢管柱受到减跨作用影响，计算长度减小，其承载力满足使用阶段受力要求。因此，可以考虑在施工阶段采取一定的措施来减小计算长度，以满足施工阶段的承载力需求。

3 利用双钢管复式钢管柱模型的计算方法

3.1 双钢管复式钢管柱

双钢管复式钢管混凝土是在普通钢管混凝土中增加圆钢管形成的一种新型结构形式，如图2 所示。复式钢管柱具有比较好的力学性能，其承载力高于相同含钢量条件下单钢管混凝土柱的承载力。因此，考虑从洞桩法车站钢管柱的施工条件及结构条件上分析是否符合双钢管复式钢管柱的结构形式。

图2 复式钢管柱

3.2 工程条件

（1）本项目车站800mm 钢管柱是在外层直径2000mm 的钢护筒保护下施工的，先施工钢护筒，再定位施工钢管柱，两者之间回填细砂填充，而细砂对钢管柱的约束几乎是没有任何刚度的，所以在此阶段，钢管柱计算长度是从柱顶到柱底，长细比较大，进而影响其承载力。若在两钢管之间填充同标号的C50 混凝土，则其结构形式上就成了双钢管复式钢管柱。

（2）由于钢管柱与钢护筒施工过程中不在同一标高上，若按照双钢管复式钢管柱考虑，上部顶纵梁荷载全部加在内圈钢管柱顶部。根据蔡绍怀[3]的实验研究成果：荷载分别加载在钢管柱壁上、柱内核心混凝土上以及均匀加载在柱壁及柱芯混凝土上对于钢管柱的极限承载力相差不超过7%，可以认为顶纵梁加载在内圈钢管柱顶部的加载模式对整个双钢管复式钢管柱的极限承载力的影响是有限的。

3.3 计算方法及结果

经过试验验证，目前对于双钢管复式钢管柱的承载力计算有两种方法比较合理：

（1）利用极限平衡理论的叠加原则，按单钢管的承载力计算方法叠加多层钢管的套箍效应。

复式钢管混凝土短柱承载力按式（5）计算：

式中：Ac1、Ac2为外层、内层混凝土面积，mm2；为外层、内层混凝土套箍极限抗压强度，kN/mm2。

（2）考虑复式钢管柱的承载力是内层混凝土极限承载力与外层混凝土极限承载力之和，其各层混凝土的极限承载力利用《钢-混凝土组合结构设计规程》（DL/T 5085-1999）相关公式计算[4]。复式钢管混凝土短柱承载力按式（6）计算：

式中：ψ 为轴压构件稳定系数；N内、N外为内层、外层混凝土承载力，N；分别按式（7）、式（8）计算。

式（7）～（8）中：Asc内、Asc外分别为内层、外层混凝土截面积，mm2；fscy内、fscy外分别为内层、外层混凝土套箍极限抗压强度，kN/mm2。

计算得出：N内=16636kN，N外=118773kN。

根据上述计算，在复式组合结构模型下，仅内层钢管柱即可满足施工阶段承载力要求；另外，两者计算结果后者略大，但是总体相差不大，因此两种计算方法均可采用。

4 结束语

（1）对于洞桩法中某些外部荷载较大、钢管柱长度较长（一般三层结构及以上），应验算施工阶段钢管柱承载力，其承载力极限值可能会小于使用阶段的承载力极限值。（2）采用极限平衡理论的叠加原则，利用多层套箍作用的计算公式，可根据具体施工条件修正后在计算中使用。（3）在施工阶段，洞桩法钢管柱的承载力可通过与钢套筒的组合结构模型计算。利用与钢套筒组合结构形成的复式钢管柱，明显提高了施工阶段钢管柱的承载力，进而提高了地铁车站的空间利用率。