基于块体二维图形的岩块三维筛分尺寸研究

2020-05-28荆永滨冯兴隆张凯铭刘锦艳

金属矿山 2020年4期

荆永滨冯兴隆张凯铭刘锦艳

（1.河南工程学院安全工程学院，河南郑州451191；2.金属矿山安全与健康国家重点实验室，安徽马鞍山243000；3.云南迪庆有色金属有限责任公司，云南香格里拉674400）

破碎岩石是采矿工程中最基本的过程，对岩石破碎后块度分布的研究是分析破碎机理、优化破碎方法和进行放矿管理的重要内容。爆破后对爆堆矿岩块度分布的准确估算，可以指导爆破设计参数的优化，实现爆破效果的最优化。合适的岩石块度分布有利于岩石破碎后续的装卸、运输和加工等工序，从而实现整个采矿过程生产成本的降低，资源利用率的提高[1-3]。此外，崩落法开采中，放矿口矿岩的块度分布影响放出体形态、放矿漏斗尺寸和放矿间距[4-5]。

岩石块度分布研究最准确的方法是筛分法和物理测量法，但这些方法成本高、效率较低，并且对生产过程产生干扰，仅在特殊需求下使用[6]。图像分析法是利用图像分割或边缘检测等算法获得岩块的弦长和面积等一维、二维参数，仅通过这些参数本身不能对破碎矿岩的块度进行定量评价[7-8]。必须通过统计分析方法进一步确定一维、二维参数与其三维参数的定量关系，将图像分析获得的二维参数转换成块体的三维尺寸，得到三维筛分尺寸作为块度特征参数的岩石块度分布。在通过岩块的一维、二维参数计算岩块三维尺寸的研究中，通常采用块体形状假设方法，即将块体假定为球、立方体或椭球体等单一形状，但实际工程中矿岩破碎后的形状差别较大，难以获得较为准确的岩块三维筛分尺寸[9-10]。

因此，本项目采用岩块三维模拟方法建立块体集合，在块体形状分类方法的基础上，对全部块体利用一组平面进行切割，得到块体对应的二维轮廓线，根据块体二维轮廓线和块体三维模型分别计算块体的二维和三维几何特征值，从而利用统计分析和回归分析建立二维和三维几何特征值之间的关系。最终实现通过块体的二维特征估算三维特征参数，最终得到定量的矿岩块度分布。

1 块体特征参数

1.1 块度参数

根据实验检验和理论分析的结果，通过图像分析法得到的岩块随机切割弦长drnd、最大切割弦长dmax和投影面积A与岩块的体积V呈较好的线性相关性，通常用这些参数作为岩块的几何特征参数。

1.2 形状参数

块体的二维形状特征参数为φ，计算公式如下：

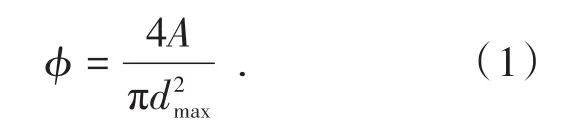
块体的三维形状特征参数为容积系数κ和共线性ε，利用κ和ε联合起来对块体进行形状分类。

块体容积系数κ反映了块体的扁平度，计算公式如下：

式中，lmax为块体最大弦长。块体的共线性值ε反映块体形状是否细长，利用2条长弦的向量和计算：

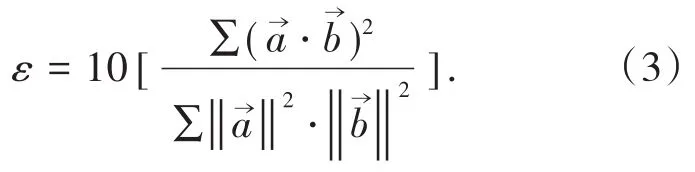
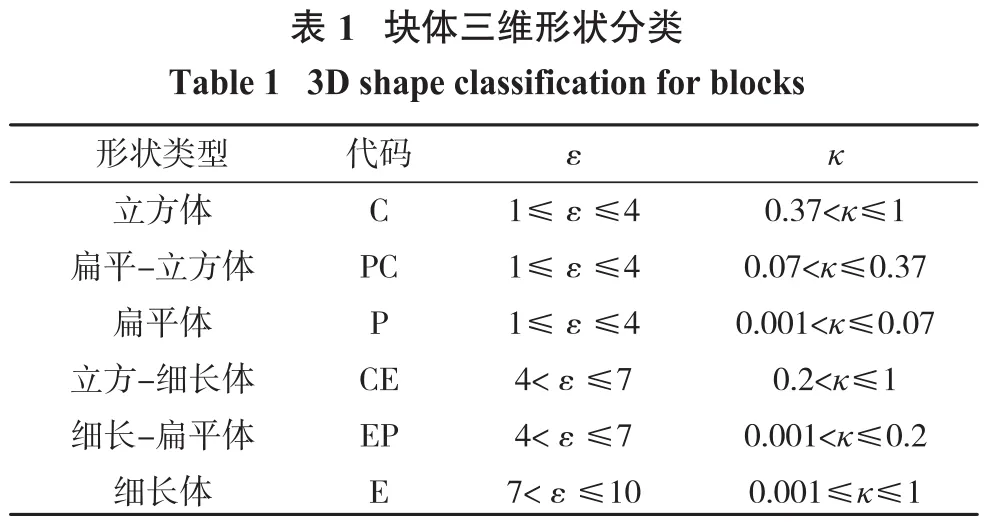
利用κ和ε联合起来将块体形状分为6种，见表1。

1.3 块体等效尺寸

矿岩块度组成通常以大于块体的最大尺寸的块体的体积或质量的百分比来确定，可能造成较大尺寸的块体所占百分比升高。因为块体通过格筛的可能性不仅取决于块体的最大尺寸，还与块体的形状有关。例如，对于形状为球体、立方体块体，其三向尺寸等于或接近于块体的最大尺寸，大于格筛尺寸的块体无法通过。而对于扁平体、细长体，三向尺寸中有2项尺寸与最大尺寸相差较大，当最大尺寸大于格筛尺寸而其余2项尺寸小于格筛尺寸时，块体有一定的可能性通过格筛。矿山实际放矿过程中，岩块经过碰撞、研磨使其可能沿最大尺寸断裂，从而增加细长块体通过漏斗的可能性。因此，在统计矿岩块度组时，增加利用块体三维形状参数进行分类的结果，进一步计算块体的等效尺寸Se。将块体等效尺寸作为过筛块度尺寸。对于不同形状类型的块体，等效尺寸计算如下：

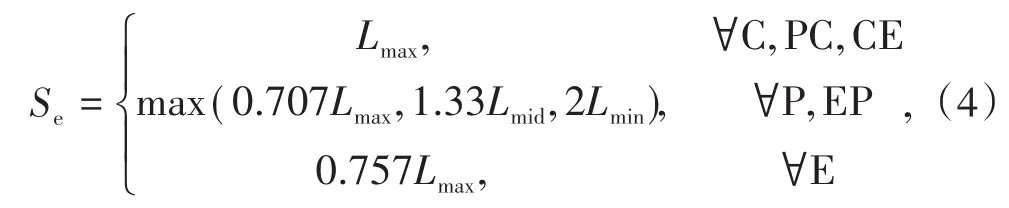
式中，Lmax，Lmid和Lmin分别为块体的最大、中间及最小尺寸。

2 岩块三维模拟

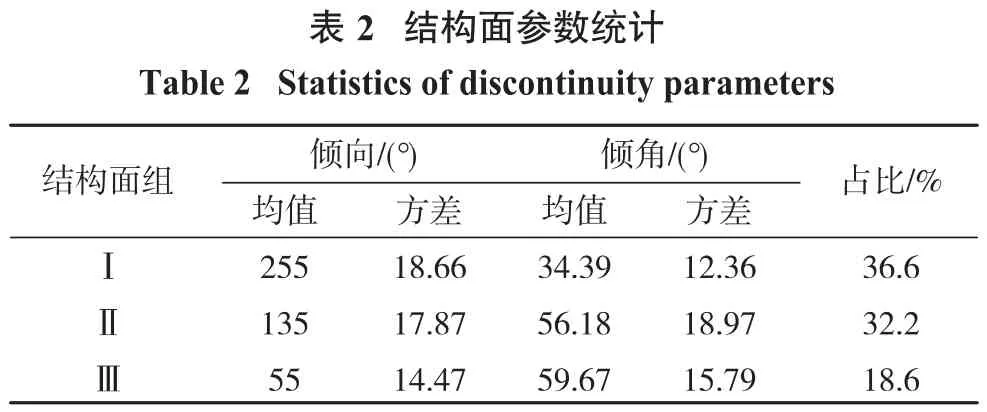
岩块三维模拟基于岩体内存在的结构面空间分布统计规律，利用三维可视化建模方法创建岩块三维模型集合。利用经过结构面切割得到的岩体原始岩块集合，研究通过岩块二维几何参数计算岩块的块度分布情况[11-12]。表2为某矿首采区结构面空间特征值统计结果，3组结构面的倾向、倾角和间距分布形式均为正态分布，结构面间距均值0.20，方差0.02。通过随机模拟建立结构面网络模型，然后利用多面体切割算法经过多次切割后建立原始三维岩块集合，如图1所示。

分别计算每个块体的容积系数κ和共线性ε，根据三维形状指标分类方法将块度三维模型分成6个岩块集合，如图1所示。

3 二维切割尺寸与三维筛分尺寸分析

二维切割尺寸是根据二维切割面积计算的岩块尺寸S2d，三维筛分尺寸S3d是根据块体形状分类结果，将块度尺寸重新计算后的等效尺寸。

3.1 最优形状假设

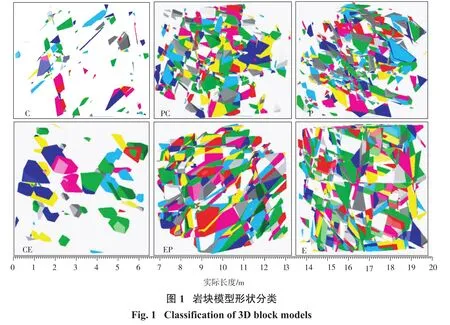
图像分析法研究中包括几种估计岩块尺寸的方法，如等同圆的直径法、等同立方体边长法、等同椭圆的直径法和平均椭圆直径法等。根据岩块计算的三维筛分尺寸S3d和根据几种假设应用二维切割面积计算的岩块尺寸S2d，它们之间的关系如图2所示。

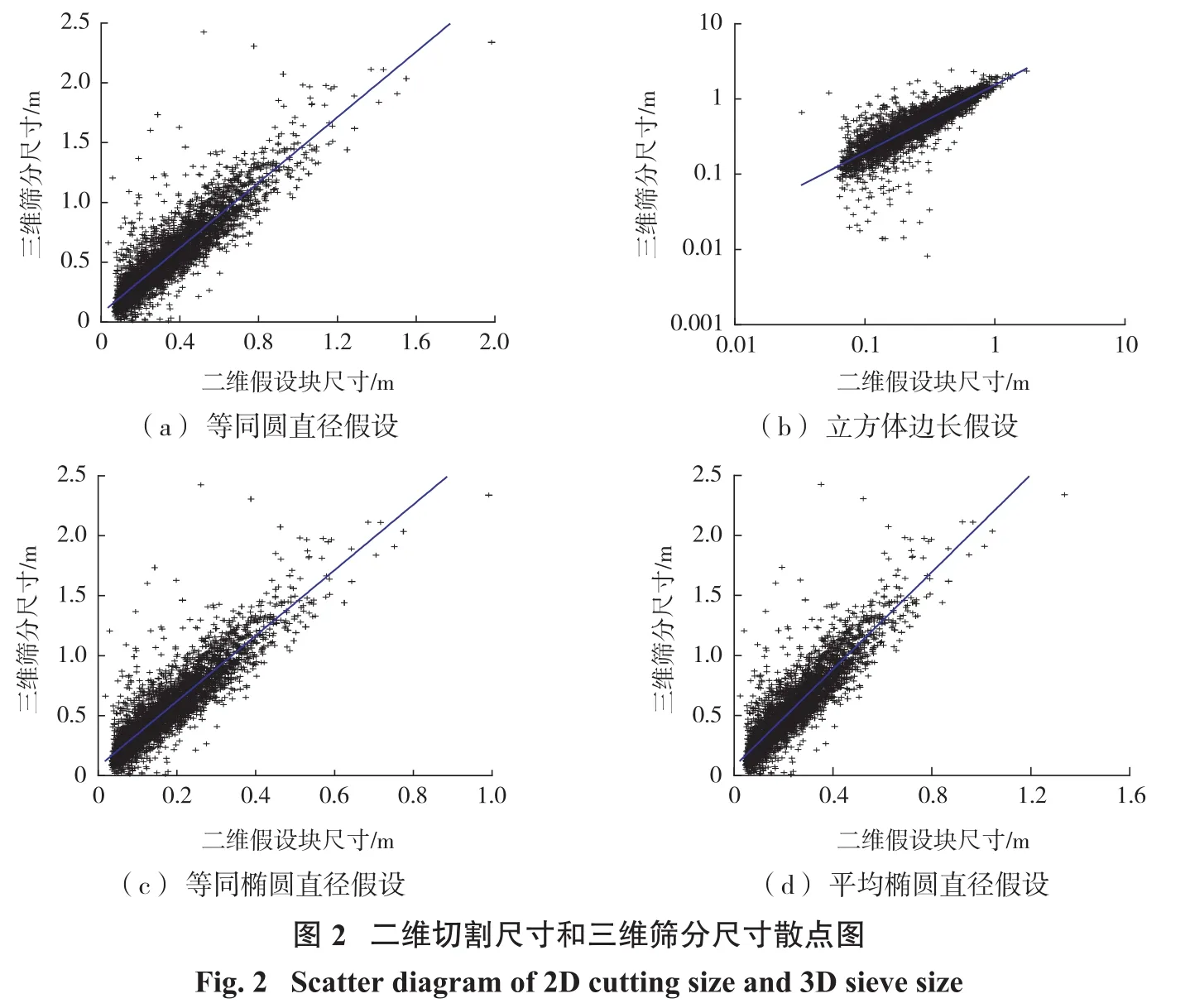
由图2可知，二维切割尺寸和三维筛分尺寸之间存在较为明显的的线性关系，其中等同圆假设、等同椭圆假设和平均椭圆假设下两者之间的关系可以表示为

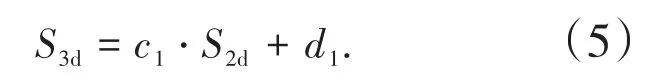
等同立方体边长假设表示为

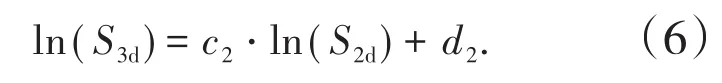
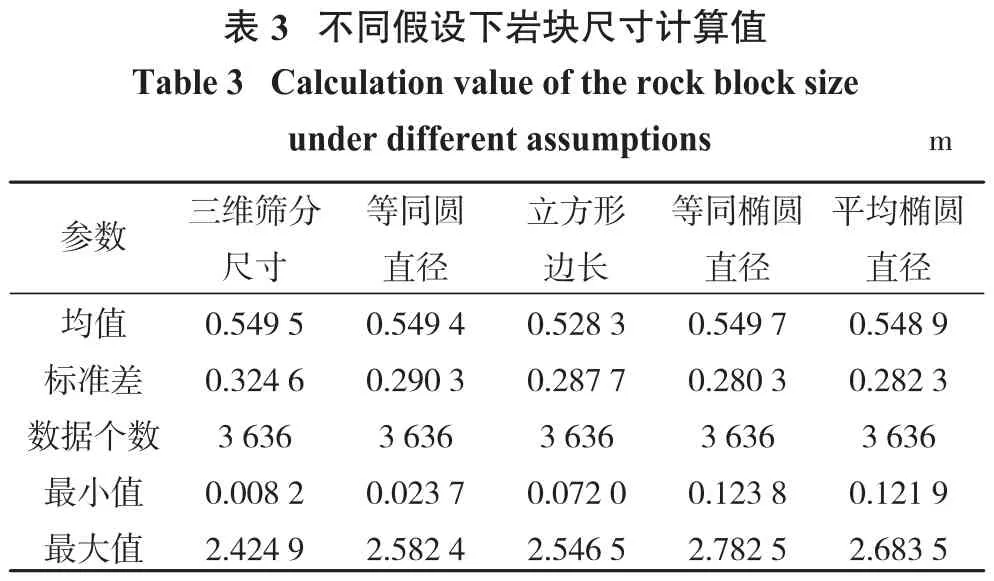
应用各种假设计算的岩块尺寸以及岩块的三维筛分尺寸统计结果见表3。

由表3可知，等同圆直径假设下计算的岩块尺寸与三维筛分尺寸接近度优于其他几种假设。

3.2 三维筛分尺寸计算

球形假设下，根据岩块的二维切割面积计算块体二维切割尺寸的公式如下，通过图像分割算法计算。

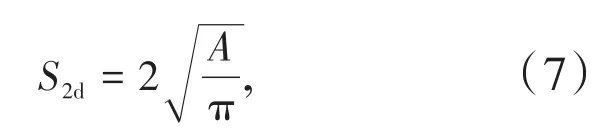
式中，A为岩块的二维切割面积。

将二维形状特征参数φ在0～0.6的范围内分成6组，分别绘制二维切割尺寸和三维筛分尺寸散点图，见图3，曲线拟合公式可以表示为

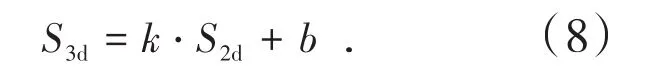
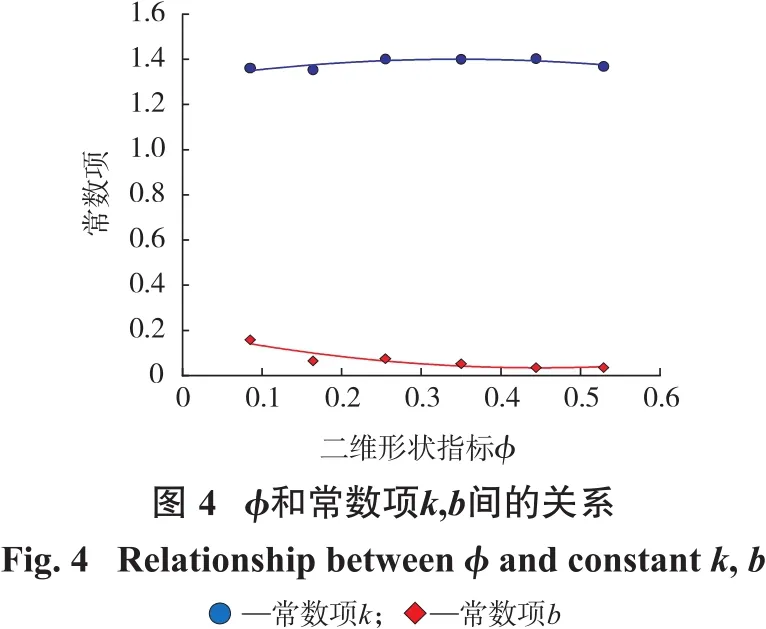
式中，k、b为未知的常数项。分别计算每一组对应的k、b值，二维形状特征参数φ与2个常数的关系如图4所示，拟合的公式见式（9）和式（10）。

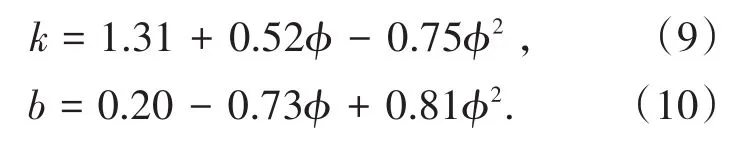
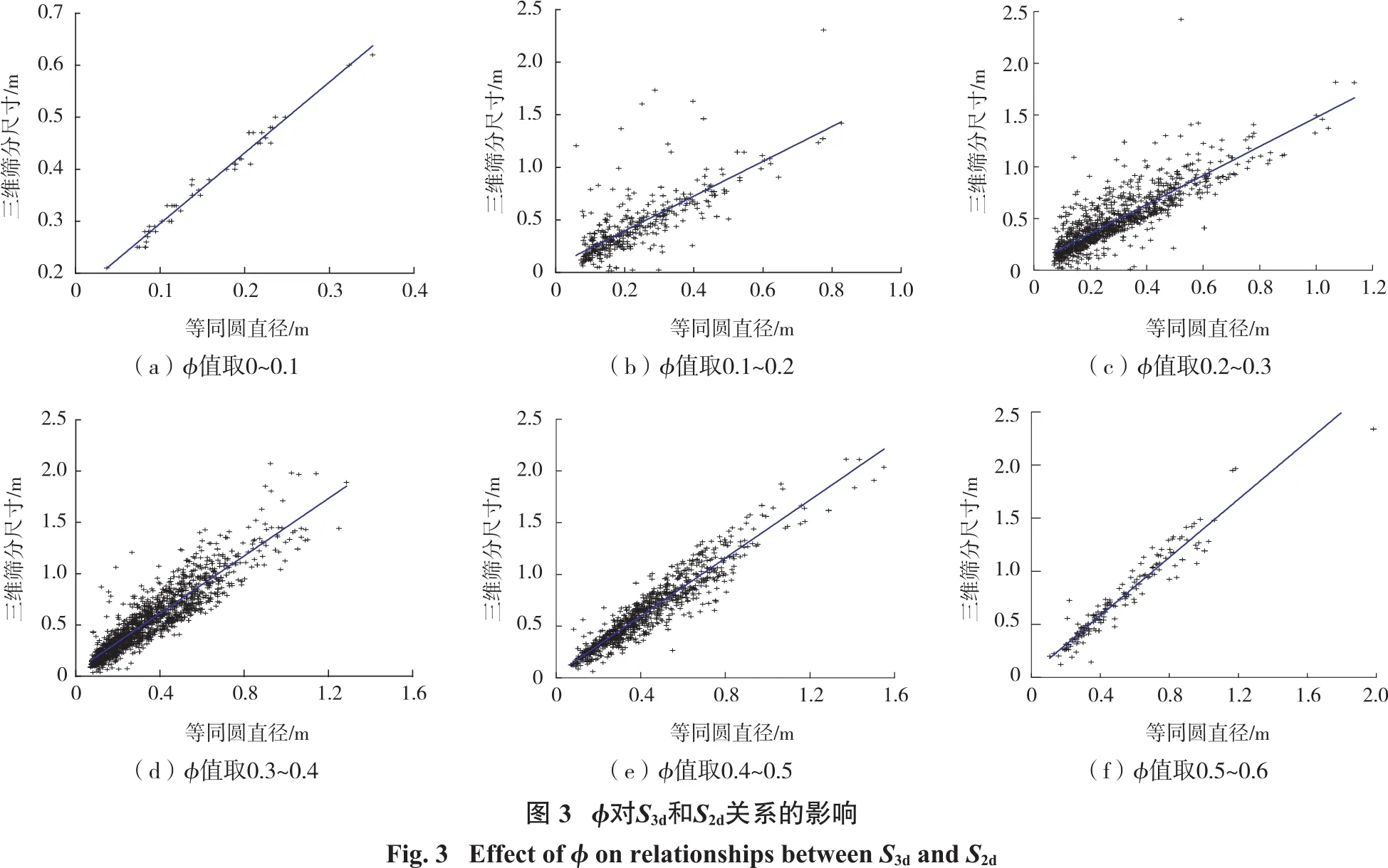
联合式（7）～式（10），三维筛分尺寸可以表示为

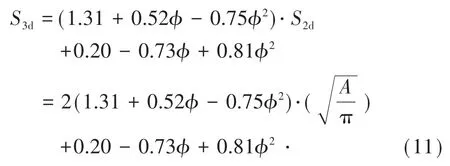
根据式（11），利用岩块切割的轮廓面积和二维形状特征参数即可计算岩块的三维筛分尺寸。

4 筛分尺寸估算结果验证

为了验证岩块筛分尺寸的计算公式，利用Monte Carlo随机模拟建立岩体中的结构面网络，然后利用结构面平面多次切割后建立三维岩块集合。3组结构面的倾向、倾角和间距分布形式均为正态分布，结构面间距均值0.22，方差0.017，结构面空间特征参数见表4。

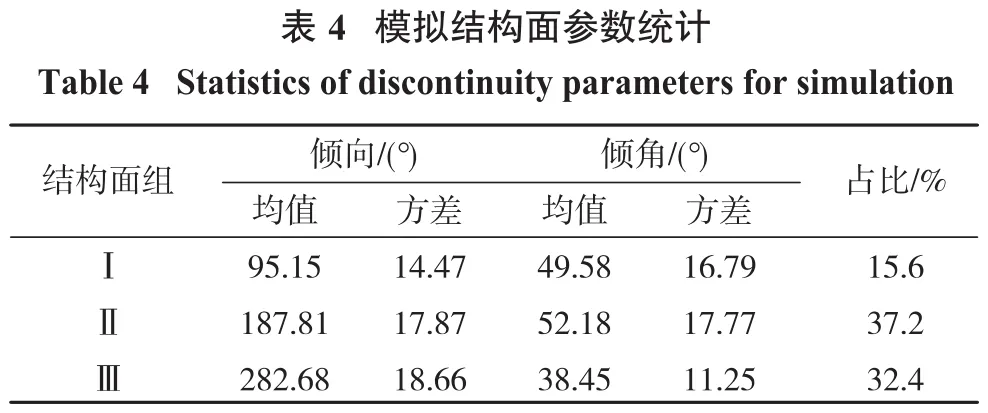
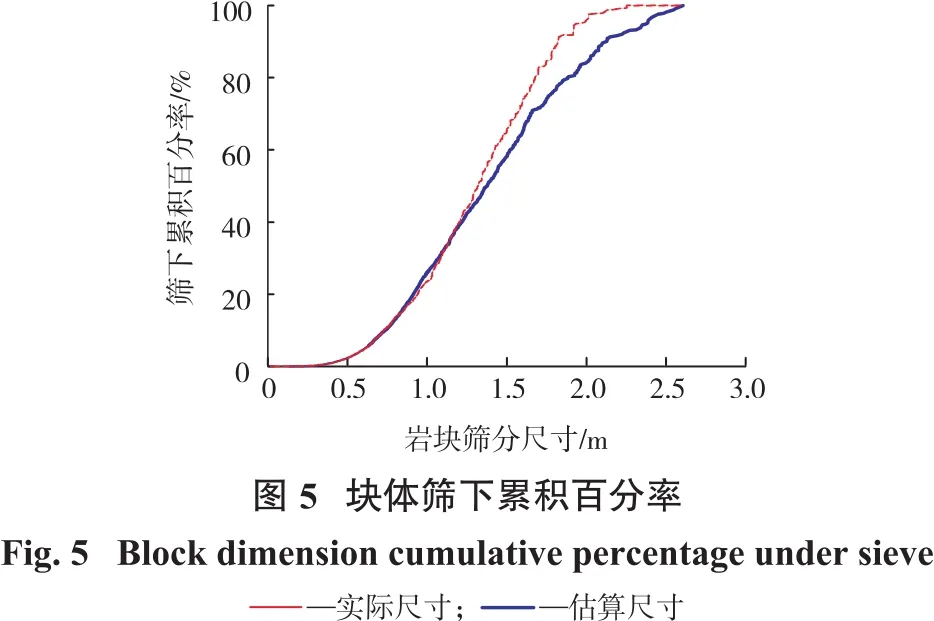
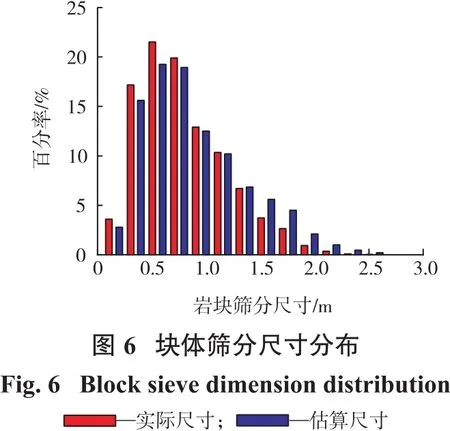
构建一组平面，平面方位角和倾角分别为90°和150°，对三维岩块集合进行切割，每个块体被平面切割后得到对应的二维轮廓线。计算岩块切割二维轮廓线的二维形状特征参数φ和面积，利用式（11）计算岩块的筛分尺寸。将岩块按照块体的三维形状特征参数容积系数κ和共线性ε进行形状分类，计算岩块的等效尺寸作为实际筛分尺寸。岩块估算尺寸和实际尺寸筛下累计百分率曲线和块度尺寸的分布直方图如图5、图6所示。从图上可见，估算的尺寸分布规律和实际尺寸的分布规律基本一致。