基于小波理论的舰船IMU加速度计信号处理算法

徐博，刘斌*，刘德政，崔耀虎，邓伟

1 哈尔滨工程大学 自动化学院，黑龙江 哈尔滨 150001

2 天津津航技术物理研究所，天津 300192

0 引 言

由于惯导系统工作环境的复杂性，加速度计信号在采集和传输过程中不可避免地存在噪声，而如何去除加速度计数据中的噪声分量，成为捷联惯性导航系统（以下简称“捷联惯导系统”）中数据处理的一项关键技术。本文将从舰船捷联惯导系统对加速度参数高分辨率、宽动态范围的设计要求入手，研究并完成舰船惯导加速度计输出信号的高精度采集与处理工作。对惯导系统而言，惯性器件的测量精度不仅包括相关惯性元件本身的精度，还包括其数据采集系统的精度，如何利用小波分析在信号处理中的优越性来实现惯导信号的高精度采集与处理，已成为惯性技术领域的一个研究热点和方向。

在捷联惯导系统中，机械结构谐振、传感器噪声和温度漂移等都是影响导航精度的主要原因，如何消除惯导系统在信号采集过程中产生的噪声影响成为实现高精度导航的关键[1]。目前，在此系统中通常采用FIR滤波[2]、最小均方（LMS）[3]、维纳（Wiener）滤波[4]、卡尔曼滤波（Kalman filter）[5]、粒子滤波（particle filter）[6]等方法对惯导加速度计信号进行降噪处理。其中，FIR滤波可以对信号进行线性相位滤波，可通过设计数字滤波器的方式将信号与噪声分离，然后保留某一频段内的信号作为输出。但这种方法只适用于有用信号和噪声的频谱没有重叠的情况，而且所需要的滤波器阶数较高，这会使得整个处理过程计算量较大，很难满足系统实时性的要求[7]。

小波降噪理论在近几年得到了迅猛发展。1994年，Donoho正式解释了“小波降噪”的含义，即通过对小波系数进行阈值量化处理来实现分层滤波的效果[8]。Mallat是最早将计算机理论中的多尺度分析思想引入小波分解过程中的人，并于1994年提出了小波分解与小波重构的快速算法，也即Mallat算法[9]。随后，斯坦福大学以Donoho为首的学术团体又提出了小波阈值滤波算法，并取得了大量的理论及实际应用成果[9]。

基于上述研究，本文拟提出一种新型的小波阈值降噪算法，该算法能对信号中的高斯白噪声等噪声进行有效滤除，并能在一定程度上避免经典去噪方法造成的信号高频部分信息丢失，可满足信号处理的实时性要求。

1 小波去噪理论

1.1 小波阈值去噪方法

小波阈值滤波的原理是：通过小波分解，在小波域内把有用信号的能量集中在一些幅值较大的小波系数上，而白噪声的能量却分布在整个小波域内，且分解后有用信号的小波系数幅值要大于噪声信号的系数幅值。因此，应通过在不同尺度上选取合适的阈值来对小波系数进行处理，若小波系数小于该阈值，则判断为噪声分量，将其置零，保留大于该阈值的小波系数，从而实现对噪声的抑制。最后，进行小波逆变换，完成信号的小波重构过程。

含噪的一维信号模型可表示为如下形式：

由图1可知，小波阈值去噪过程的一般步骤如下[10]：首先，对原始含噪信号进行多尺度的小波分解；然后，根据信号特征计算得到各尺度下的小波阈值估计值，并对各分解尺度下的小波系数进行阈值量化处理；最后，将完成阈值处理后的各层小波系数进行重构运算，得到去噪后的输出信号。在这3个步骤中，最关键的步骤是阈值估计以及如何对小波系数进行阈值处理，在某种程度上，它关系到信号降噪的质量。

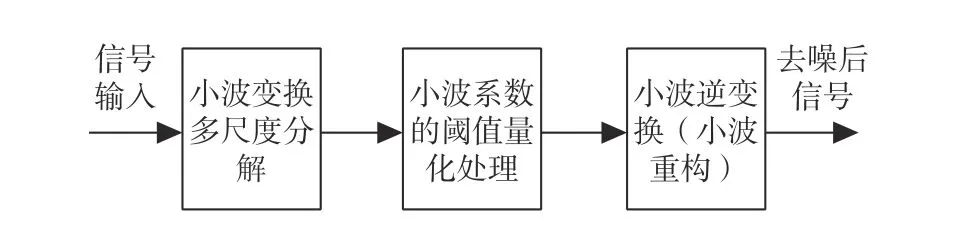
图 1 小波去噪流程图Fig. 1 Flow chart of wavelet denoising

1.2 改进型小波阈值滤波

小波阈值滤波的关键在于阈值估计以及阈值函数的选取。目前，常用的阈值处理方法有2种：硬阈值函数和软阈值函数。

硬阈值函数[11]：

图 2 3种阈值函数对比Fig. 2 Comparison of three threshold functions

利用不同阈值函数对同一噪声信号进行处理，处理结果如图3所示，并将不同阈值函数处理所得误差进行对比，如图4所示。

利用各种阈值函数对Heavisine信号去噪后的信噪比（signal to noise ratio，SNR）和均方根误差（root mean squared error，RMSE）如表1所示。

从图3、图4和表1中可以看出：硬阈值函数去噪后的波形中存在较多毛刺，信号平滑性较差；通过软阈值函数处理得到的信号波形虽然光滑，但信号重构精度较差，信噪比较低；利用新型阈值函数处理得到的信号较为光滑，SNR和RMSE均优于其他阈值函数，并且计算相对简便，具有更高的实用价值。

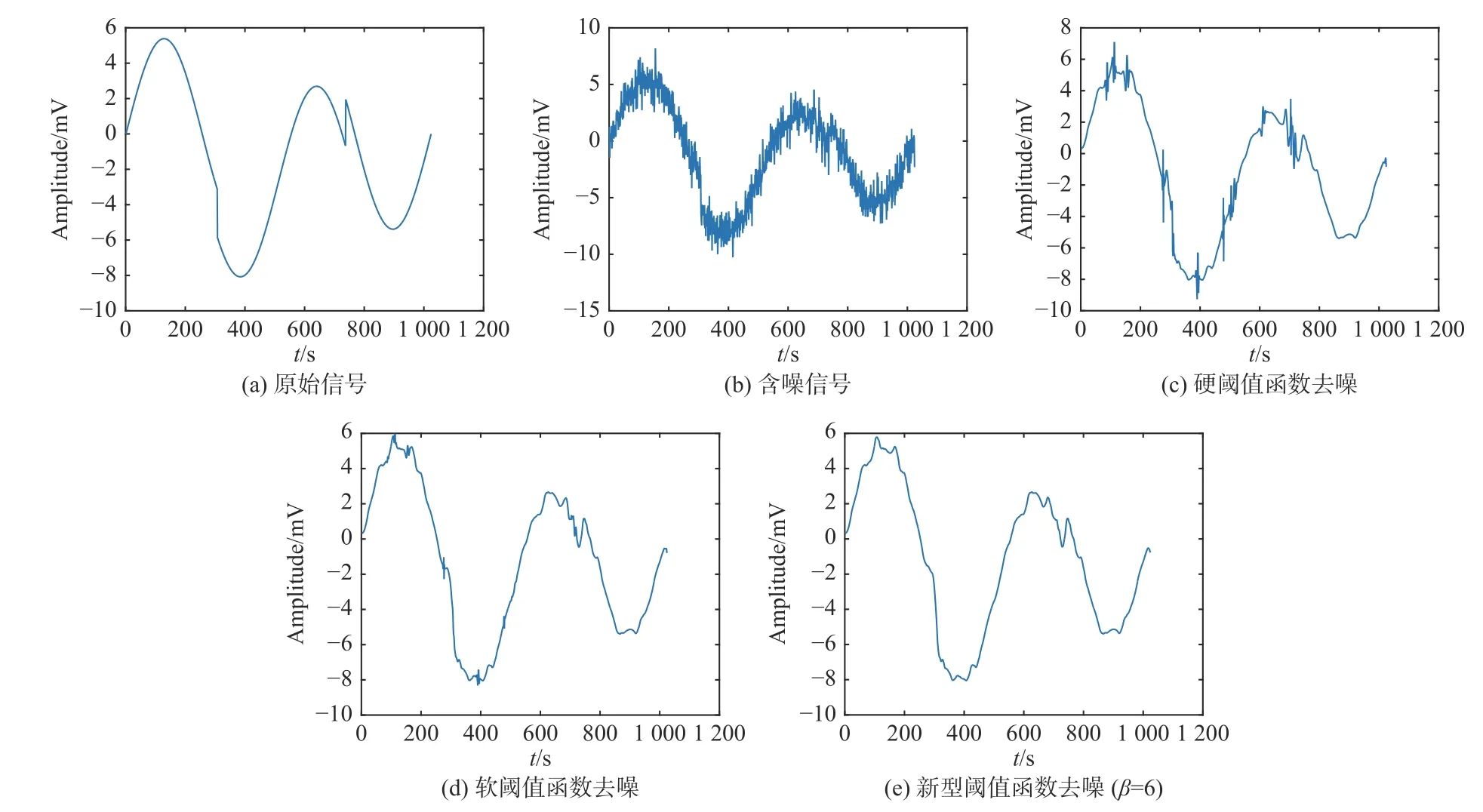
图 3 不同阈值处理函数的去噪效果比较Fig. 3 Comparison of denoising effects of different threshold processing functions

图 4 不同阈值处理函数误差对比图Fig. 4 Error comparison of different threshold processing functions

表 1 不同阈值函数去噪后信噪比和均方根误差比较Table 1 Comparison of SNR and RMSE after denoising by different threshold functions

2 基于Mallat算法的小波降噪FPGA实现

2.1 Mallat算法

为实现信号的快速分解与重构，Mallat将多尺度分析的思想引入到了小波分析中并提出了Mallat算法[13]。根据Mallat算法，小波分解的数学表达式为

由于滤波器长度有限，为便于计算，分别将小波分解和重构表达式转换成了易于实现的形式，即

根据Mallat算法理论，本文选用DB3小波基对经过A/D转换后的加速度计信号进行三阶的小波分解与重构。

2.2 延拓模块

在Mallat算法的推导中，是假定输入序列为无限长，而在实际应用中，输入序列为有限长，此时，滤波器系数与输入序列进行卷积就会出现“轮空”现象。因此，可在设计中采用对称延拓的方法来减少在边界处的卷积误差，从而有效避免输入序列边缘不连续的问题。

由于设计中采用的是DB3小波基，其对应的滤波器长度为7，因此原始信号两端需要延拓的数据长度为5（filterLen-1）。ModelSim仿真结果如图5所示。

图 5 延拓仿真图Fig. 5 Extension simulation diagram

2.3 滤波器模块

无论是小波分解还是重构，都是通过数字滤波器来实现的，滤波器模块是整个运算的核心部分。由式（7）和式（8）可知小波分解和重构的实质都是卷积运算，由于小波基选择的是DB3，为优化结构设计，需要设计5级流水的滤波器，主要由乘法器和加法器组成。

在滤波器设计过程中，涉及到浮点数的运算，通过研究对比现有的基于FPGA的浮点运算方法[14]，在本设计中，首先将滤波器系数量化成16位精度模式，然后在滤波器中对卷积运算的输出数据作截取处理，即右移16位作为滤波结果。其中，小波重构低通滤波器ModelSim仿真结果如图6所示。

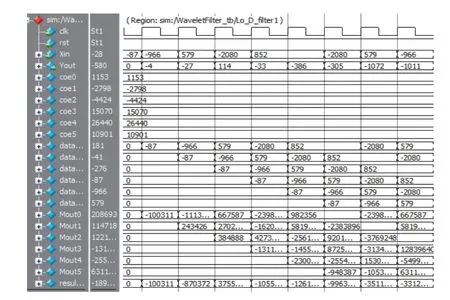
图 6 低通滤波器ModelSim仿真Fig. 6 Low-pass filter ModelSim simulation

2.4 阈值处理模块

小波去噪的关键在于阈值的确定以及阈值函数的选取。为保证各尺度下小波阈值的准确性，本文采用分层阈值估计方法，其函数表达式为

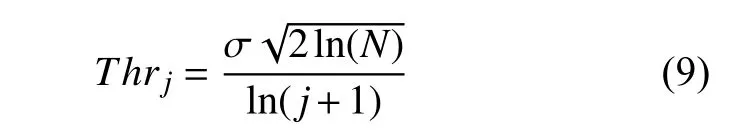
式中：N为采样点数；σ为信号噪声标准差。但在实际工程中，噪声标准差是不知道的。如果采用硬件计算方法求解阈值，不仅需要对噪声进行估计，还需要进行开根号等运算，硬件实现相对复杂[15]。利用Matlab软件对加速度计数据进行分析，计算出不同尺度下每一分解层不同的阈值，然后再将计算得到的阈值存入FPGA的参数RAM中，在进行小波阈值处理的过程中，直接从RAM中完成读取。

图7所示为新型小波阈值去噪FPGA实现流程图。该模块的具体设计办法为：首先，将各层小波系数进行相应的移位和带符号位扩展，实现对各层小波系数绝对值与已设定相应层阈值大小的判断[16]；然后，利用新型小波阈值处理函数对小波系数进行处理，对算法中涉及到的乘法或者除法进行运算，在设计中主要是利用FPGA内置的IP核LPM_MULT和LPM_DIVIDE实现；最后，进行位数截取以得到新的小波系数结果。

3 实验结果分析

3.1 仿真实验分析

设计中，使用Altera公司的EP4CE22F17 FPGA作为系统核心控制处理单元，系统时钟为64 MHz。在验证过程中，首先通过ModelSim和Matlab等

图 7 新型小波阈值去噪FPGA实现流程图Fig. 7 Flow chart of implementation of the new wavelet threshold de-noising in FPGA

利用改进型阈值函数法进行信号去噪处理后的信号波形得到了明显改善。为进一步反映基于FPGA实现的小波去噪算法的降噪效果，将FPGA的仿真结果以二进制文本形式保存并在Matlab中进行了分析处理，如图8所示。利用信号处理前后的RMSE和SNR这2个客观标准，进一步验证了这种阈值去噪方法的良好去噪效果，如表2所示。

图9（a）为原始带噪信号。图9（b）为经过小波降噪处理后的信号，图中对Matlab与FPGA小波实现结果进行了对比，结果显示其略有差异，这是由于在FPGA运算过程中位截断和数据取整造成了数据丢失。图9（c）为利用傅里叶分析进行滤波后的信号。从图中可以发现，该滤波器无法准确还原信号，不能将有用信号的高频突

图 8 ModelSim仿真结果Fig. 8 ModelSim simulation results

表 2 信号去噪效果比较Table 2 Comparison of signal denoising effects

图 9 小波去噪效果比较Fig. 9 Comparison of wavelet denoising effects

变部分与噪声引起的高频干扰加以区分。通过对比图9（b）和图9（c），验证了小波降噪算法具有更高的信噪比，对信号的高频突变处理效果更加显著。

3.2 加速度计测试结果分析

为验证本文所提方法在工程应用上的价值，对静态条件下的加速度计输出信号进行了采集测试，实验测试结果如图10所示。

图 10 数据对比Fig. 10 Data comparison

图10（a）为测试原始数据与小波模块处理后数据分别减掉均值后的数据分布图。从图中可以看出，未经处理的原始数据信号幅值变化较大，大部分数据在±2 000 mV范围内跳动，而经过小波降噪模块处理后的数据则相对稳定，主要在±500 mV内波动。图10（b）为利用傅里叶滤波器处理后的数据与小波模块处理后数据分别减掉其均值后的数据分布图。从图中不难看出，相比未经任何处理的原始数据，两者的信号稳定性均得到了改善，但经过傅里叶处理后的信号变化幅值还是较大，主要变化范围在±800 mV内。

现对动态条件下的加速度计输出信号进行采集测试。动态试验环境为：三轴转台模拟摇摆试验数小时，摇摆周期8 s，摇摆角度0.6°。实验测试结果如图11所示。

图 11 动态数据对比Fig. 11 Dynamic data comparison

图11（a）为测试动态情况下的加速度数据与小波模块处理后加速度数据分别减掉转台真实值后的数据分布图。从图中可以看出，未经处理的原始数据信号幅值变化较大，大部分数据在±0.001g范围内跳动，而经过小波降噪模块处理后的数据则相对稳定，主要在±0.000 2g左右波动。图11（b）为利用傅里叶滤波器处理后的数据与小波模块处理后数据分别减掉转台真实值后的数据分布图。从图中不难看出，相比未经任何处理的原始数据，两者的信号稳定性均得到了改善，但经过傅里叶处理后的信号变化幅值还是较大，主要变化范围在±0.000 4g左右。

图12所示为利用傅里叶和小波处理后的数据频谱分布图。经过上述2种滤波处理后的数据高频噪声均得到了很好的抑制，但仔细研究可以发现，传统的傅里叶低通滤波器在对信号进行处理的过程中有“一刀切”的缺点，也即保留了所有的低频信息，将通带之外的频谱不加区分地全部滤掉了，而相比傅里叶变换，小波降噪处理则显得更加灵活。由图12（b）可以看出，小波降噪处理是通过在不同尺度上选取合适的阈值来对小波系数进行处理，若小波系数小于该阈值，则判断

图 12 频谱分布Fig. 12 Spectrum distribution

为了更加直观、有效地分析小波算法的性能，分别对上述测试数据进行了计算统计，结果如表3所示。

由表3的计算结果可知，直接通过舰船IMU加速度计采集电路得到的原始数据ENOB可以达到20.8位以上；利用传统傅里叶低通滤波器和小波降噪模块均能改善信号质量，有效分辨率分别可以达到21.7位和22.4位以上，但是在计算滤波器参数时发现，因传统傅里叶滤波器的阶数较高，使得整个处理过程的计算量较大，而小波降噪模块只需要完成3层变换就可满足上述指标。因此由以上分析可以看出，小波降噪模块在信号降噪方面具有较为明显的优越性。

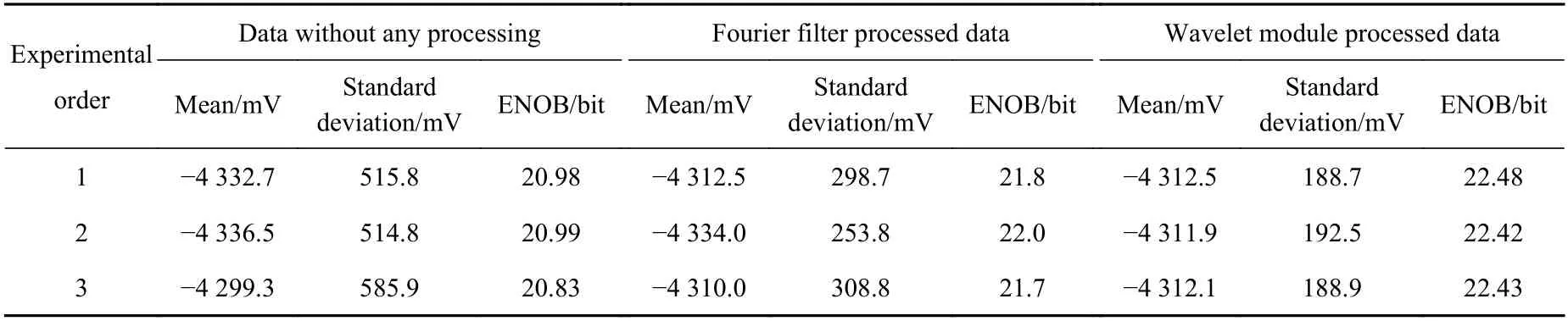
表 3 小波算法性能分析Table 3 Performance analysis of wavelet algorithm

4 结 语

本文在介绍小波去噪基本原理的基础上，提出了一种改进型小波阈值滤波算法，通过与传统的频域去噪方法进行对比验证，得出小波去噪可以很好地对高斯白噪声进行降噪处理，有效解决了传统频域滤波方法的局限性。最后，利用FPGA对小波阈值算法进行了硬件实现。实验结果表明，利用新型小波算法处理后的加速度计采集电路有效分辨位数能够达到22.4位以上，相比原始信号，其有效分辨率提高了1.6位，证明小波算法具有较好的工程应用价值。但该降噪算法的阈值估计采用的是固定阈值，在下一步的工作中，还需要对自适应阈值进行研究以满足系统动态性能要求。