间歇通信环境下的船舶编队控制
2020-05-28刘睿于双和尹广帅
刘睿,于双和,尹广帅
大连海事大学 船舶电气工程学院,辽宁 大连 116026
0 引 言
随着航海技术的发展,国内外许多学者非常关注多艘船舶编队作业的控制研究[1-2]。为实现编队控制,船舶之间需要彼此通信来获得所需的信息。在不同环境下,由于船舶通信会受到不同因素的干扰,所以需要寻找不同通信问题的解决方法[3-4]。
船舶编队控制通常包括 3种方法:领导—跟随法、虚拟结构法和基于行为的控制方法。其中,领导—跟随法[5]的应用范围最广,但是如果领导者失控,整个系统就会崩溃。而采用虚拟领航者[6]能很好地解决此问题。Fu等[7]考虑了外部干扰下船舶的编队问题,并利用神经网络估计了环境误差,但是在船舶编队中每艘船舶必须时刻与领航者保持通信,导致船舶之间的通信数据对编队的形成没有起到相应的效果,从而造成通信资源浪费。
在多船舶或多智能体的协调控制中,通信问题相对复杂[8]。间歇通信包含了正常通信时段和通信缺失时段,外部环境干扰可能会导致间歇通信的出现,同时在通信时主动采用间歇性的通信过程并设计合适的控制器,可以在保证理想通信效果的前提下减少一定的通信带宽,从而减少通信设备的损耗。Gao等[9]提出了事件触发间歇通信环境下AUV的编队控制问题,并将有限时间理论与控制器设计相结合,但是编队的鲁棒性较差,当某一AUV失去与领航者的通信后,不能通过获得其他AUV的信息实现编队。Wen等[10]提出了一阶线性多智能体在间歇通信下的一致性问题,并推广到编队及切换拓扑的一致性跟踪问题,但是并没有给出具体的通信时长约束条件。徐律等[11-12]设计了二阶多智能体在间歇通信环境下的一致性控制律,且考虑了延时等因素,但是却未考虑到多智能体受到干扰后,其稳定性的充分条件的判别标准也会随之变得复杂。Wen等[13]在考虑外部干扰下提出了二阶智能体的一致性协议。上述文献针对的都是双积分为主的模型,与实际船舶的模型相差较大,在对船舶进行研究时,推导过程会产生其他复杂的项,所以以多智能体为主的文献成果并不能很好地应用到实际船舶中。
基于以上问题,本文将对间歇通信环境下的船舶编队控制问题进行研究。首先,将图论与反步法相结合,采用误差观测器处理干扰误差,设计正常通信时段的控制律。然后,考虑通信缺失的时段,设计船舶控制律,推导出新的充分条件并予以证明,在确保合适的通信时长情况下,实现多艘船舶的编队。最后,将李雅普诺夫函数作为判断系统稳定性的常用工具,通过其导数直观反应系统的稳定性,构造李雅普诺夫函数从理论上证明每个跟随者都能指数收敛到理想的编队位置,并给出仿真验证。
1 基本概念
1.1 图 论

1.2 间歇通信定义

1.3 船舶数学模型
通常船舶在海平面的运动需要考虑3个自由度:纵荡、横荡和艏摇。在船体坐标系下,3个自由度的船舶运动模型可表示为
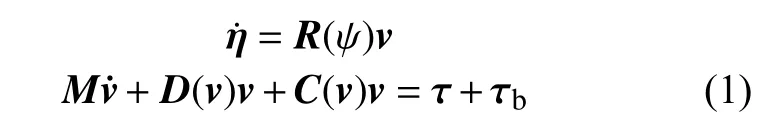
式中:η=[n,e,ψ]T,为在大地坐标系下的北方向位置、东方向位置、艏摇角;v=[u,v,r]T,为船舶在船体坐标系下的纵荡、横荡和艏摇角速度;R(ψ)为大地坐标系与船体坐标系的转换矩阵;M为质量矩阵;D(v)为阻尼矩阵;C(v)为科里奥利向心矩阵;τ=[τu,τv,τr]T,为控制输入向量;τb=[τbu,τbv,τbr]T,为包含海浪、风等的时变外部干扰,且假设干扰是有界并连续的。对船舶模型进行变换,可得:

2 主要结果
2.1 船舶编队控制律设计



2.2 间歇通信环境下的船舶编队
本节综合考虑间歇通信环境下的船舶编队问题,设计了船舶编队控制律式(18),使以式(2)为模型的船舶能够根据理想航迹的位置、速度信息以及相邻船舶的信息形成编队。此外,考虑到误差观测器的工作,在设计没有信息交流的控制律时需要区别于一般的间歇通信。



3 仿 真
本节给出仿真图来证明本文设计的船舶编队控制律的有效性。假定一共有4艘船舶和1艘虚拟领航者,船舶模型采用Cybership II[15]。仿真的各项参数如下所示。

外部环境干扰误差:
ρi(t)=[500sin(t),1200,100cos(t)]T
此外,船舶编队的通信拓扑如图1所示,并且假定船舶在通信时获得的信息是实时且准确的。

图 1 船舶通信拓扑图Fig. 1 Vessels communication topology
根据图论可知,通信拓扑图1包含虚拟领航者的拉普拉斯矩阵为


船舶编队轨迹如图2所示。由图可看见,在采用本文给出的控制律并满足通信时长的情况下,船舶能够形成编队。
每艘船舶的位置曲线如图3所示。由图可见,随着时间的推移,4艘船舶的轨迹向量最终会收敛到理想值。
每艘船舶的速度曲线如图4所示,可以看出,当控制律切换到不通信状态时,船舶的速度保持不变,恢复通信后,船舶速度可以继续跟踪理想速度。
由图2可见,每艘船各自拥有不同的初始位置,在控制律式(18)的作用下,最终形成理想的编队并且收敛到指定的轨迹,由于需要在控制中切换观测器函数和船舶的控制律,所以导致在不通信时段船舶航行轨迹会有一定程度的误差(图3和图4),但是当下一个通信周期到来时,船舶可以重新回到理想的轨迹并保持理想状态。
图5为船舶的位置跟踪误差,图6为船舶的速度跟踪误差。由图5和图6可见,在通信时段,船舶位置和速度跟踪误差会收敛到0,并且通过采用合适的控制律可以保证误差快速收敛到0,同时增大通信时间,也可以保证编队的稳定形成。

图 2 船舶编队轨迹Fig. 2 Formation trajectories of vessels
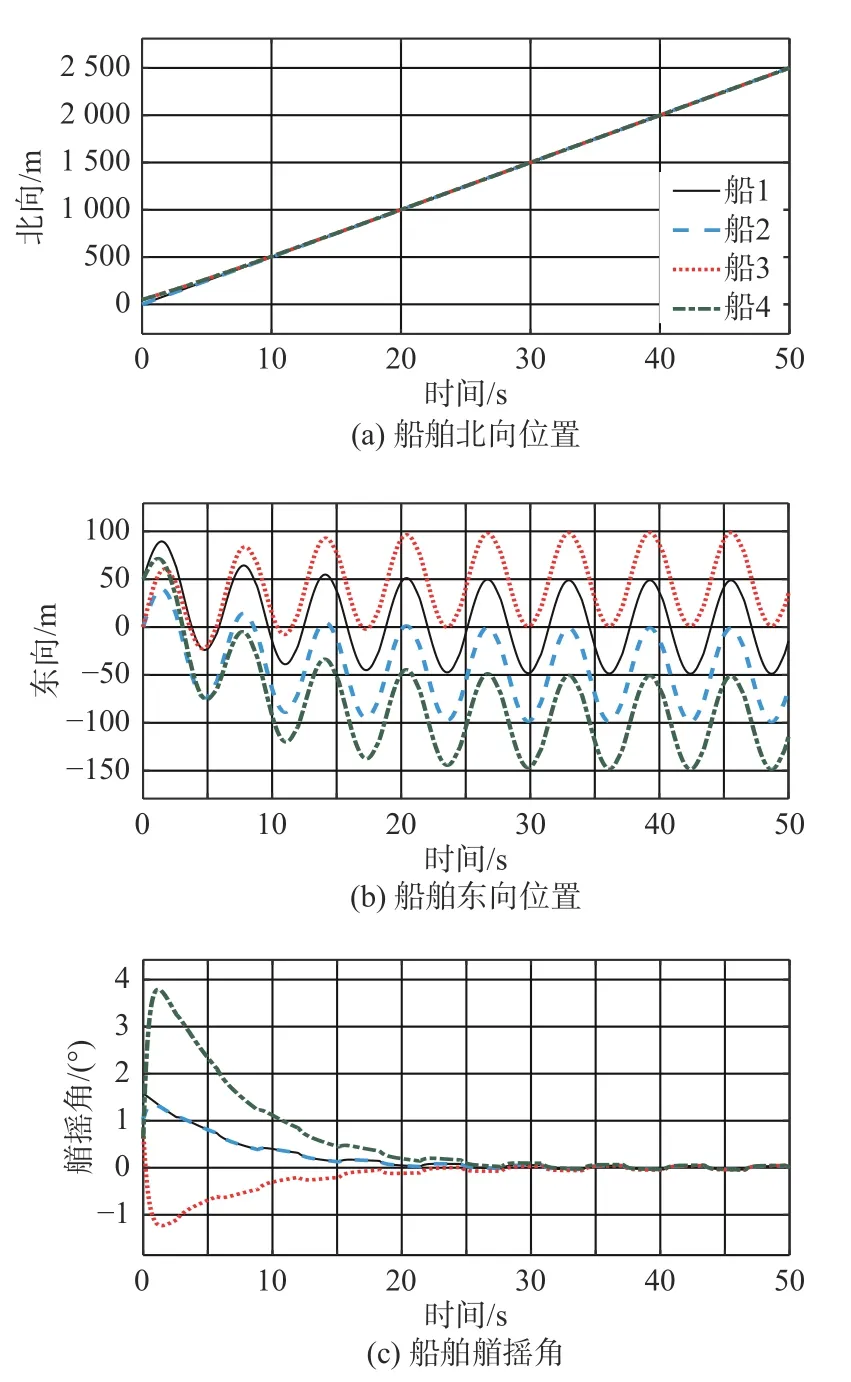
图 3 船舶位置曲线Fig. 3 Position curves of vessels
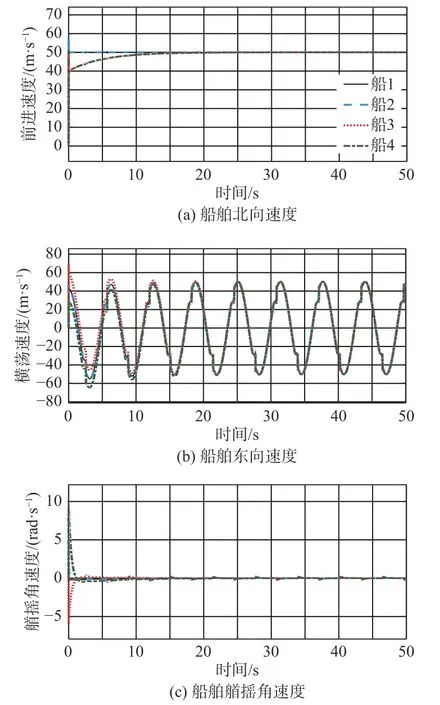
图 4 船舶速度曲线Fig. 4 Velocity curves of vessels

图 5 船舶位置跟踪误差Fig. 5 The position tracking errors of vessels

图 6 船舶速度跟踪误差Fig. 6 The velocity tracking errors of vessels
4 结 语
本文研究了在间歇通信环境下的多艘船舶的编队控制问题。考虑了实际环境中存在的外部干扰,加入误差观测器来观测外部干扰。在正常通信时段,基于图论和反步法设计编队控制律,将船舶和虚拟领航者之间的理想相对位置和速度信息作为输入,设计的控制律可以使每艘船舶到达理想的位置。在通信缺失时段,只需要利用船舶的自身信息设计控制律,给出满足编队形成的充分条件并予以证明。利用李雅普诺夫方程,对所提出的控制律的稳定性进行严格的分析,保证船舶编队以指数形式收敛到理想位置并跟随理想轨迹。未来将考虑对间歇通信中存在的延时、噪声等问题进行研究,使之具有更广泛的意义。
