正戊烷异构化制异戊烷反应热力学分析
2020-05-27刘洪全于中伟马爱增张秋平孙义兰王子健
刘洪全, 于中伟, 马爱增, 张秋平, 孙义兰, 王子健
(中国石化 石油化工科学研究院,北京 100083)
C5/C6异构化是将C5和C6正构烷烃转化为相应的异构烷烃的过程。异构化油具有硫含量低、不含烯烃和芳烃的特点,是理想的高辛烷值汽油调和组分,可提高发动机的前端辛烷值和启动性能[1-3]。近年来,随着我国汽油升级步伐的加快,C5/C6异构化作为油品升级不可或缺的技术之一,越来越引起人们的重视。目前,已工业应用的C5/C6异构化技术,按催化剂体系可分为3类[4],分别是中温分子筛异构化、固体超强酸异构化和低温异构化。中温分子筛异构化技术通常以负载Pt或Pd的沸石分子筛为催化剂,反应温度为513.15~553.15 K、反应压力为1.6~3.0 MPa、氢/烃摩尔比为1~2。固体超强酸异构化技术以负载Pt的硫酸化氧化锆为催化剂,反应温度为413.15~473.15 K、反应压力为1.6~3.5 MPa、氢/烃摩尔比为1~2。低温异构化技术通常以负载Pt的氯化氧化铝为催化剂,反应温度为393.15~443.15 K、反应压力为2.5~3.5 MPa、氢/烃摩尔比为0.05~0.5。
目前有关C5/C6异构化反应热力学研究报道较少,仅有的几篇文献基本采用了假设反应物为气相,且为理想气体的方式进行计算和分析[5-6]。而从现有 C5/C6异构化技术来看,反应温度范围为393.15~553.15 K、压力为1.6~3.5 MPa、氢/烃摩尔比为0.05~2,反应温度较低而压力较高,在这样的条件下,如果不考虑反应物和产物的非理想性,可能会产生较大偏差,无法很好指导实验研究。笔者以正戊烷为研究对象,结合实际反应体系,进行正戊烷异构化反应热力学分析,为C5/C6异构化反应工艺条件优化提供参考。
1 热力学分析方法
对于正戊烷异构化反应,主反应为正戊烷异构化生成异戊烷。采用现有的3种异构化技术时,该反应选择性都很高,因此在热力学分析中仅考察正戊烷异构化生成异戊烷的反应,不考虑其他副反应。
1.1 反应的和值的计算
假设反应为气相反应,且正戊烷和异戊烷均为理想气体,根据Kirchhoff公式,反应体系的摩尔焓变ΔrHm(T)的表达式如式(1)所示。

(1)
式(1)中,Cp,i为参加反应各物质的等压摩尔热容,其表达式如式(2)所示。
Cp,i=ai+biT+ciT2
(2)
式(2)中,ai、bi和ci是经验常数,由各组分本身的特性决定。
通过查阅物理化学数据手册[7-8],可以得到正戊烷异构化反应中各组分的典型热力学数据,将不同温度下各组分的等压摩尔热容值代入式(2),进行线性回归,可以得到常数ai、bi和ci的值,结果列于表1。

表1 由式(2)计算得到的正戊烷和异戊烷的等压摩尔热容的经验常数Table 1 The empirical constants of constant pressure molar heat capacity of n-pentane and isopentane calculated by Eq.(2)
将式(2)代入式(1),并进行积分,可得式(3)。
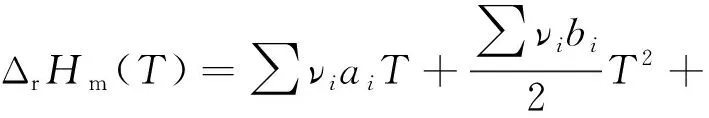
(3)
Δa=∑νiai
Δb=∑νibi
Δc=∑νici
式(3)中,I1为积分常数,可将标准摩尔生成焓数据代入求得。将Gibss-Helmholtz公式(式(4))代入式(3),并进行积分,可得式(5)。
(4)
(5)
式(5)中,I2为积分常数,可将标准摩尔生成吉布斯自由能数据代入求得。将理想气体体系标准平衡常数的定义式(式(6))代入式(5),可得正戊烷异构化反应标准平衡常数与温度的关系式(7)。
(6)
(7)
1.2 反应体系的化学平衡和相平衡
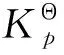
(8)
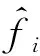
(9)
(10)
由于正戊烷异构化反应压力较高而反应温度较低,正戊烷和产物异戊烷有可能以气-液两相存在。在这种情况下,反应过程不仅存在化学平衡,还存在相平衡。组分i相平衡的条件是其在各相中的化学势相等,对于气-液两相体系,可用式(11)表示。将混合物中组分i逸度的定义式(12)[9]代入式(11),得到另一个等效的以逸度表示的相平衡判据,如式(13)所示。将式(13)用逸度系数表示,则变为式(14)。
μiV=μiL
(11)
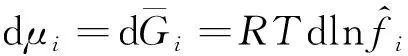
(12)
(13)
(14)
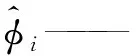
汽化平衡比Ki的定义式如式(15)所示。从式(10)和式(15)可以看出,反应平衡常数Kf和汽化平衡比Ki由各组元的平衡浓度和逸度系数决定。
(15)
1.3 组元逸度系数的计算方法
逸度系数可利用状态方程来计算,对于烃类体系,选用Soave-Redlich-Kwong(SRK)状态方程较为合适[10-11]。SRK状态方程的标准形式见式(16),其多项式形式见式(17)。
(16)
z3-z2+(A-B-B2)-AB=0
(17)
式(16)和(17)中,参数λ、γ、A和B的表达式分别如式(18)~(21)所示。
(18)
γ=0.08664RTc/pc
(19)
A=λαp/R2T2
(20)
B=γp/RT=0.08664pr/Tr
(21)
SRK状态方程式(16)中的α称为Alpha方程,Alpha方程为温度的函数,在应用时可根据物质的种类选择不同的Alpha方程用于计算。对于烃类,笔者采用Soave[12]给出的Alpha方程,如式(22)所示;对于氢气,采用Twu等[13]提出的Alpha方程,如式(23)所示。
(22)
(23)
对于混合物,SRK状态方程式(16)中λα和γ的表达式分别如式(24)和(25)所示。
λα=∑∑yiyj(λα)ij
(24)
γ=∑yiγi
(25)
式(24)中的(λα)ij可由式(26)表示,式(26)中的kij是与浓度无关的交互作用参数,对于烃类和氢气,取kij值为0。
(26)
用SRK状态方程求取组元逸度系数的通式见式(27)[14]。
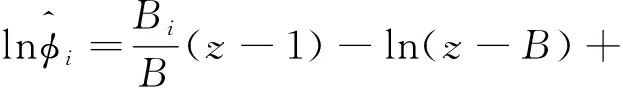
(27)
式(27)中,Bi可表示为式(28)。
Bi=γip/RT
(28)
从上述公式可知,应用SRK状态方程求取逸度系数,需要各组元的物性参数,包括临界温度Tc、临界压力pc和偏心因子ω。本文中正戊烷和异戊烷的物性参数引自文献[15],氢气的物性参数引自文献[8]。
1.4 反应平衡组成的计算
如前所述,正戊烷异构化反应可能是气相、液相或气-液两相,要计算反应平衡组成,首先要判断反应条件下的相态,而要判断反应相态,则要计算反应体系的露点和泡点。
在特定的反应条件下,由反应进度可得到如式(29)所示的各组元的物质的量。
ni=ni0+ενi
(29)
式(29)中,νi对反应物为负值,对产物为正值,由于表观上氢气不参与异构化反应,其赋值为0。
如果反应体系为气-液两相,则各组元的总物质的量为气相物质的量和液相物质的量之和,由式(30)表示。
(30)
各组元的物料衡算如式(31)所示。
ni=nLxi+nVyi=[nL+Ki(nt-nL)]xi
(31)
由于摩尔分数的总和应等于1,由式(31)可得到式(32)。
(32)
分别将式(29)和式(30)代入式(32),可得式(33)。
(33)
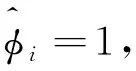
如果指定反应温度和起始组成,采用上述步骤可计算露点压力。以nL值逼近nt为条件,采用上述步骤也可计算反应体系的泡点。
如果反应处于露点和泡点之间的两相区,则可采用上述计算露点温度方法中的(1)~(4)步来计算出平衡组成。
2 结果与讨论
2.1 正戊烷异构化反应的热效应
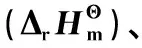
表2 不同温度下正戊烷异构化反应的标准摩尔焓变标准摩尔吉布斯自由能变和标准平衡常数值Table of n-pentane isomerization at different temperatures
2.2 反应体系相态的判断
按照1.4节的方法计算了各典型反应压力和氢/烃摩尔比条件下反应体系的露点温度,结果如表3所示。由于氢气的存在,反应体系的泡点温度不易精确求出,但通过1.4节的计算可以判断表3所列压力和氢/烃摩尔比条件下的泡点温度均低于273.15 K。

表3 不同压力和氢/烃摩尔比(n(H2)/n(HC))下正戊烷异构化反应的露点温度(Td)Table 3 Dew temperatures (Td) of n-pentane isomerization at different pressures and n(H2)/n(HC)
1), 2), 3), 4)—n(H2)/n(HC) value
从表3可知,反应压力和氢/烃摩尔比均对露点温度有显著的影响,相同压力下氢/烃摩尔比越高露点温度越低,而相同氢/烃摩尔比下压力越高露点温度越高。
利用表3数据还可以判断现有异构化技术的相态。在反应压力为1.6~3.5 MPa、氢/烃摩尔比为1~2的条件下,体系的露点温度最高达408.05 K,低于现有中温异构化和固体超强酸异构化的反应温度,因此可判断在中温异构化和固体超强酸异构化的反应条件下,正戊烷异构化为气相反应。从表3还可以看到,在反应压力为2.5~3.5 MPa、氢/烃摩尔比为0.05~0.5条件下,体系的露点温度范围为388.45~456.95 K,而低温异构化的反应温度为393.15~443.15 K,二者的温度范围有重叠,因此可以判断低温异构化反应体系可能为气相或气-液两相。
2.3 反应温度对正戊烷异构化反应的影响
在反应压力为3.0 MPa、氢/烃摩尔比为0.5的条件下,计算了反应温度对正戊烷异构化反应的影响。
首先计算了不同温度下反应的相态、各相占比及组成,结果如表4所示。从表4可以看到:反应温度为323.15~413.15 K时,反应体系呈气-液两相;随着温度升高,更多的液相组分被汽化,气-液两相的摩尔比逐渐增加。此外,在该温度范围内,气相中氢气的含量随着反应温度的升高而下降,而液相中的氢含量则先升高后下降,在393.15 K左右达到最高。

表4 不同反应温度下正戊烷异构化反应的相态、各相以及每相中各组分的平衡摩尔分数Table 4 Phase states, equilibrium molar fractions of different phases and components in each phase for n-pentane isomerization at different reaction temperatures
p=3.0 MPa;n(H2)/n(HC)=0.5
图1给出了不同温度下正戊烷异构化反应的平衡异构化率,曲线(1)是假设反应体系为理想气体的计算结果,曲线(2)是考虑体系的非理想性、用SRK方程进行计算的结果。从图1可以看出,无论采用哪种假设,正戊烷的平衡异构化率都随着反应温度的升高而降低,说明正戊烷异构化反应在热力学上是低温有利的。反应温度高于423.15 K时,两条曲线基本重合,说明高于该温度时反应体系的非理想性并不明显,可参照理想气体来计算。而当反应温度低于423.15 K时,采用SRK方程计算出的平衡异构化率低于理想状态的计算结果,且温度越低,差异越大。在前述3种异构化技术中,低温异构化的反应温度通常低于423.15 K,因此其反应体系的非理想性不可忽略。

图1 正戊烷异构化反应中平衡异构化率随反应温度(T)的变化Fig.1 Equilibrium isomerization ratio vs Tfor n-pentane isomerization(1) The reaction system is considered as ideal gas; (2) The nonidealityof the reaction system is considered using SRK equationp=3.0 MPa; n(H2)/n(HC)=0.5
2.4 反应压力对正戊烷异构化反应的影响
在反应温度为403.15 K、氢/烃摩尔比为0.5的条件下,计算了反应压力对正戊烷异构化反应的影响。
首先计算了不同温度下反应的相态、各相占比及组成,结果如表5所示。从表5可以看出,在低压下,反应体系呈气相,随着压力升高,反应体系由气相转变为气-液两相,且液相的比例随着压力的进一步升高而增加,液相中氢的浓度也随着压力的升高而略有增加。
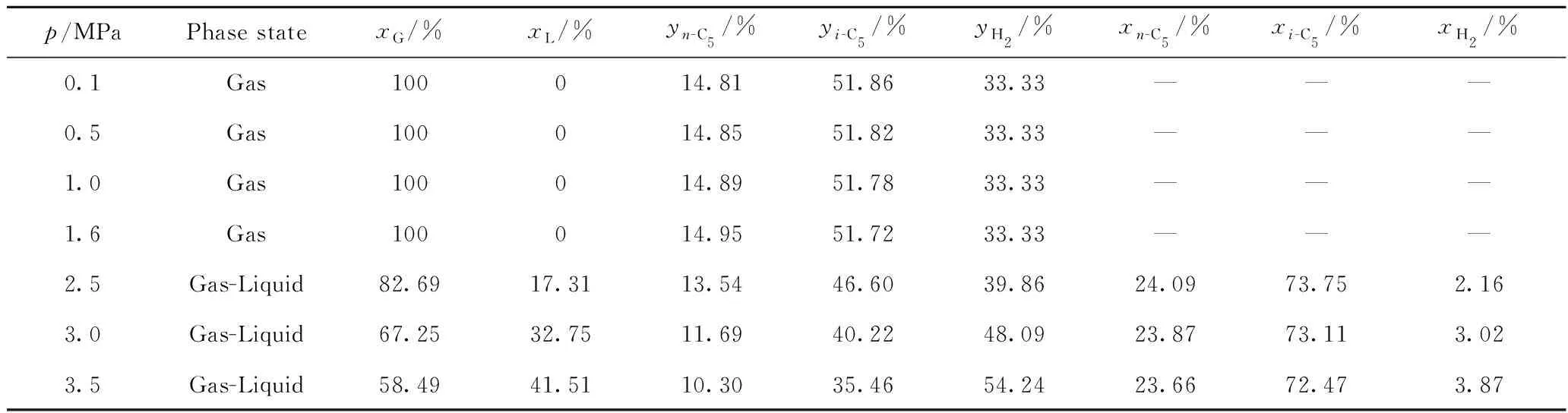
表5 不同反应压力下正戊烷异构化反应的相态、各相以及每相中各组分的平衡摩尔分数Table 5 Phase states, equilibrium molar fractions of different phases and components in each phase for n-pentane isomerization at different reaction pressures
T=403.15 K;n(H2)/n(HC)=0.5
图2是反应温度403.15 K、氢/烃摩尔比0.5条件下,正戊烷平衡异构化率与反应压力的变化关系曲线。图中曲线(1)是假设反应体系为理想气体的计算结果,曲线(2)是基于SRK方程的计算结果。从图2可以看出,理想状态下反应压力对正戊烷的平衡异构化率没有影响。当采用SRK方程计算时,压力低于1.6 MPa时的计算结果与理想气体的结果基本一致,说明反应温度为403.15 K、反应压力低于1.6 MPa时,反应体系的非理想性也可以忽略。而当反应压力高于1.6 MPa时,采用SRK方程计算出的正戊烷平衡异构化率随着反应压力的升高而下降,说明高压下反应体系的非理想性逐渐显现,且提高压力对反应平衡不利。
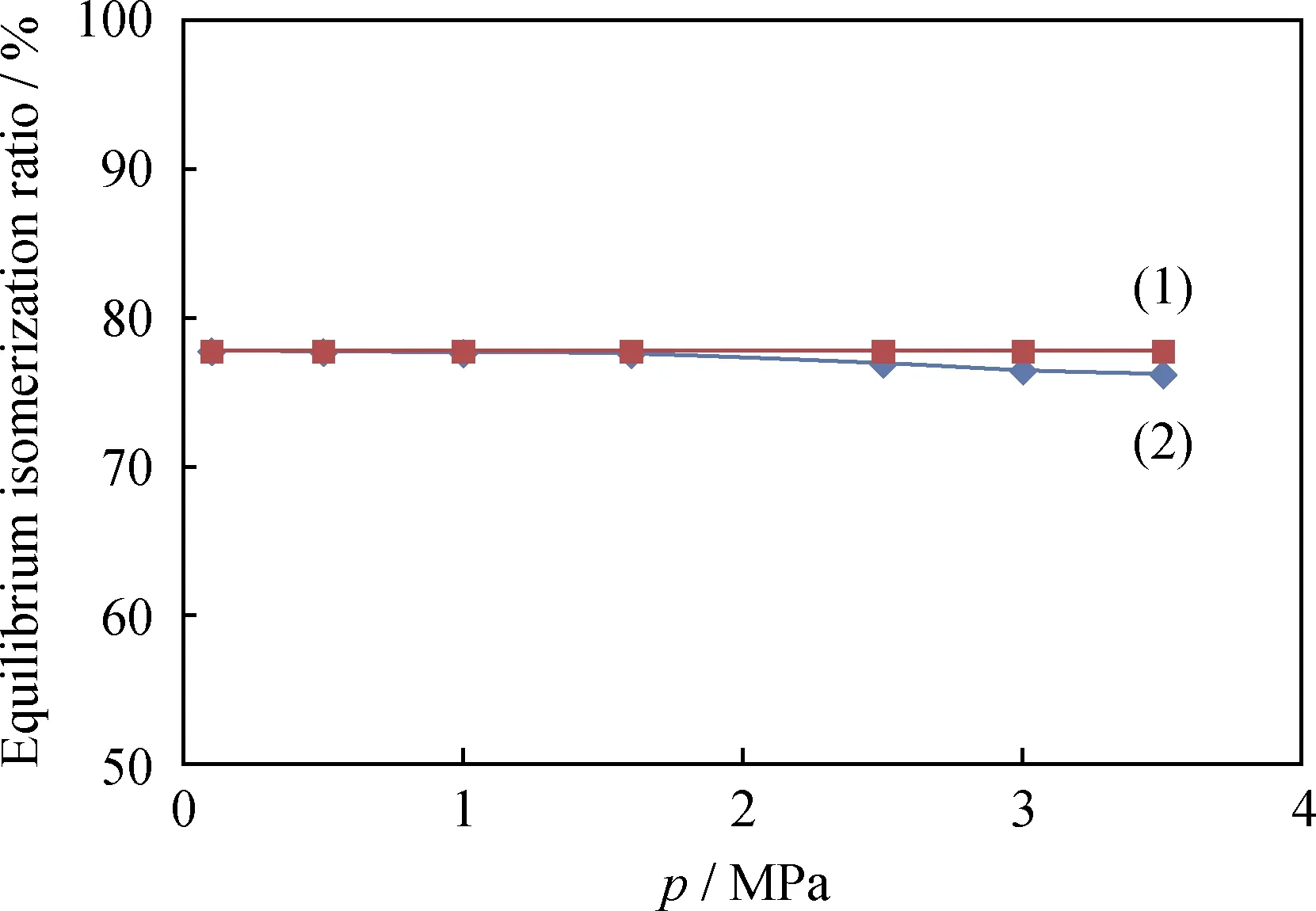
图2 正戊烷异构化反应中平衡异构化率随反应压力(p)的变化Fig.2 Equilibrium isomerization ratio vs pfor n-pentane isomerization(1) The reaction system is considered as ideal gas; (2) The nonidealityof the reaction system is considered using SRK equationT=403.15 K; n(H2)/n(HC)=0.5
2.5 氢/烃摩尔比对正戊烷异构化反应的影响
在反应温度为403.15 K、反应压力为3.0 MPa的条件下,计算了氢/烃摩尔比对正戊烷异构化反应的影响。
首先计算了不同温度下反应的相态、各相占比及组成,结果如表6所示。从表6可以看出:在氢/烃摩尔比高于1.0时,反应体系为气相;随着氢/烃摩尔比下降,反应体系由气相转变为气-液两相,当氢/烃摩尔比为0.5时,液相摩尔分数为32.75%;进一步降低氢/烃摩尔比,液相比例进一步增加,当氢/烃摩尔比为0.05时,液相摩尔分数高达96.14%。此外,值得注意的是,在氢/烃摩尔比为0.05~0.5时,气-液两相中各组分的平衡摩尔分数基本保持不变。
图3给出了不同氢/烃摩尔比条件下正戊烷异构化反应的平衡异构化率。曲线(1)是假设反应体系为理想气体的计算结果,曲线(2)是基于SRK方程的计算结果。从图3可以看出,理想状态下氢/烃摩尔比对正戊烷的平衡异构化率没有影响。采用SRK方程计算时,当氢/烃摩尔比高于1.0时,其计算结果与理想状态的基本一致;而当氢/烃摩尔比低于1.0时,正戊烷平衡异构化率随氢/烃摩尔比的降低而下降,说明低氢/烃摩尔比时反应体系的非理想性比较明显,且降低氢/烃摩尔比对反应平衡不利。
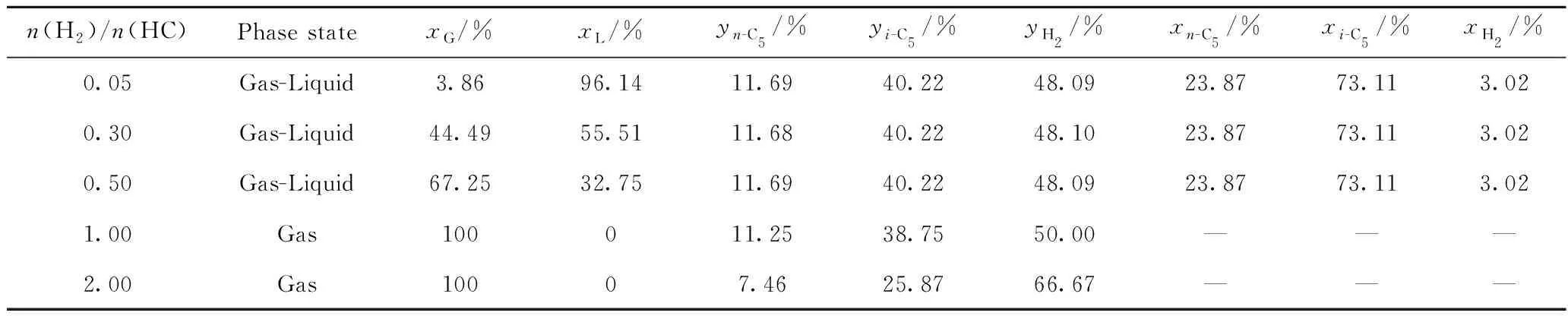
表6 不同氢/烃摩尔比(n(H2)/n(HC))下正戊烷异构化反应的相态、各相以及每相中各组分的平衡摩尔分数Table 6 Phase states, equilibrium molar fractions of different phases and components in each phase for n-pentane isomerization with different n(H2)/n(HC)
T=403.15 K;p=3.0 MPa
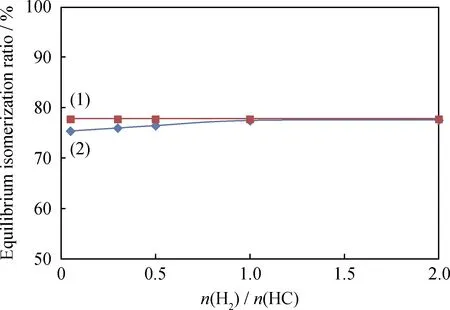
图3 正戊烷异构化反应中平衡异构化率随氢/烃摩尔比(n(H2)/n(HC))的变化Fig.3 Equilibrium isomerization ratio vs n(H2)/n(HC)for n-pentane isomerization(1) The reaction system is considered as ideal gas; (2) The nonidealityof the reaction system is considered using SRK equationT=403.15 K; p=3.0 MPa
3 结 论
(1)正戊烷异构化属微放热反应,温度是最敏感的反应参数,降低反应温度可显著提高正戊烷的平衡异构化率。
(2)对于正戊烷中温分子筛异构化、固体超强酸异构化和低温异构化3大反应体系,前两者为气相反应,气体的非理想性不明显,可假设其为理想状态进行热力学分析;后者为气相或气-液两相反应,气体的非理想性较明显,采用理想状态假设进行热力学分析偏差较大。
(3)当体系非理想性不明显时,反应压力和氢/烃摩尔比对正戊烷平衡异构化率的影响可以忽略;当体系非理想性较为明显时,反应压力和氢/烃摩尔比对反应平衡的影响不可忽略。适当降低反应压力或提高氢/烃摩尔比均可提高正戊烷的平衡异构化率。
符号说明:
ai——等压摩尔热容表达式中经验常数,J/(K·mol);
Δa——∑νiai的简略表达,J/(K·mol);
A——SRK状态方程参数;
Bi——SRK方程中i的参数B;
bi——等压摩尔热容表达式中经验常数,J/(K2·mol);
B——SRK状态方程参数;
ci——等压摩尔热容表达式中经验常数,J/(K3·mol);
Cp,i——参加反应各物质的等压摩尔热容,J/(K·mol);
ΔrCp,m——反应的等压摩尔热容变,J/(K·mol);

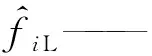
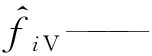
ΔG——吉布斯自由能变,J/mol;

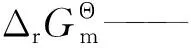
ΔH——焓变,J/mol;
ΔfHm,i(T0)——为温度为T0时参加反应各物质的摩尔生成焓,J/mol;
ΔrHm(T)——反应温度为T时的摩尔反应焓变,J/mol;
ΔrHm(T0)——反应温度为T0时的摩尔反应焓变,J/mol;
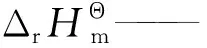
I1——积分常数,J/mol;
I2——积分常数,J/(K·mol);
Kf——用逸度表示的平衡常数;
kij——交互作用参数;
Ki——汽化平衡比;

ni——组分i物质的量,mol;
ni0——组分i初始物质的量,mol;
nL——液相物质的量,mol;
nt——总物质的量,mol;
nt0——初始总物质的量,mol;
nV——气相物质的量,mol;
pc——临界压力,Pa;
pi——组分i的分压,Pa;
pr——对比压力;
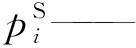
p——压力,Pa;
R——气体常数,J/(K·mol);
T0——初始温度,K;
Tc——临界温度,K;
Td——露点温度,K;
Tk——设定温度,K;
Tr——对比温度;
T——反应温度,K;
V——摩尔体积,m3/mol;
xG——气相的摩尔分数,%;
xH2——液相中氢气的摩尔分数,%;
xi——液相中组分i的摩尔分数,%;
xi-C5——液相中异戊烷的摩尔分数,%;
xL——液相的摩尔分数,%;
xn-C5——液相中正戊烷的摩尔分数,%;
yH2——气相中氢气的摩尔分数,%;
yi——气相中组分i的摩尔分数,%;
yi-C5——气相中异戊烷的摩尔分数,%;
yj——气相中组分j的摩尔分数,%;
yn-C5——气相中正戊烷的摩尔分数,%;
z——SRK状态方程参数;
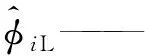
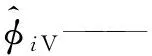
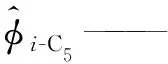
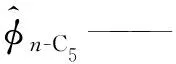
α——SRK状态方程参数;
γ——SRK状态方程参数,m3/mol;
γi——SRK方程中i的参数γ,m3/mol;
ε——反应进度,mol;
λ——SRK状态方程参数,Pa·(m3/mol)2;
(λα)ij——SRK方程表达混合物时组分i与组分j的交叉参数,Pa·(m3/mol)2;
(λα)i——SRK方程中组分i的参数λ与α的乘积,Pa·(m3/mol)2;
(λα)j——SRK方程中组分j的参数λ与α的乘积,Pa·(m3/mol)2;
μiL——液相中组分i的化学势;
μiV——气相中组分i的化学势;
μi——组分i的化学势;
νi——化学反应式中各组分的计量系数,对反应物为负值,对产物为正值,对不参与反应的物质为0;
ω——偏心因子。
